Convolutional Neural Network
- Convolution Layer: 네트워크가 비전 태스크를 수행하는 데에 유용한 Feature들을 학습할 수 있도록 함 : 비전 분야의 대표적인 Backbone
- Activation Function: 네트워크에 비선형성을 가해주는 역할을 함
- Pooling Layer: Feature Map에 Spatial Aggregation을 시켜줌
Convolution Layer
- 네트워크가 비전 태스크를 수행하는 데에 유용한 Feature들을 학습할 수 있도록 함
- Filter(=Kernel): Input Image를 특정 크기의 Filter를 이용하여 탐색하면서 Convolution 연산을 시행하여 Filter 영역에 대한 특징을 추출하게 된다.
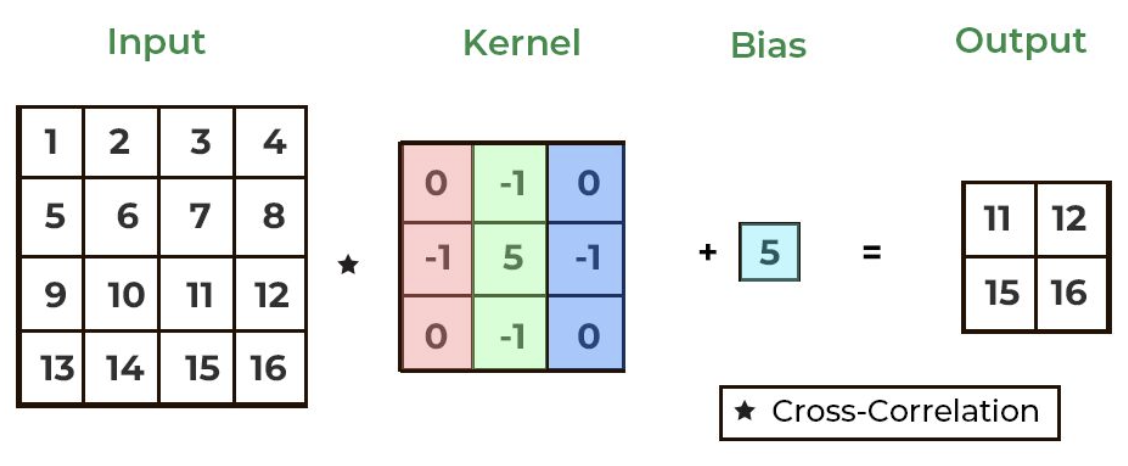
- Stride (S): Filter를 얼마만큼의 간격으로 움직이는 지를 나타냄
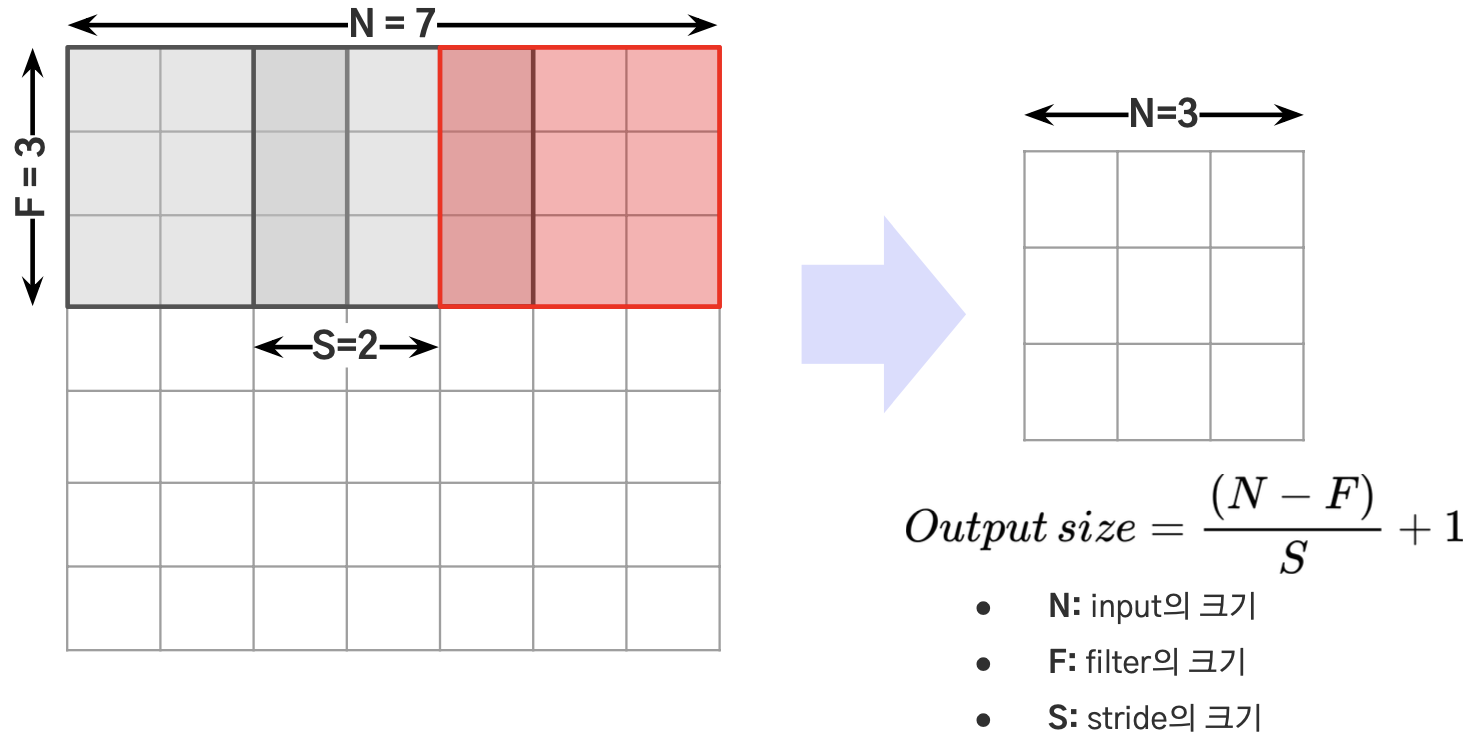
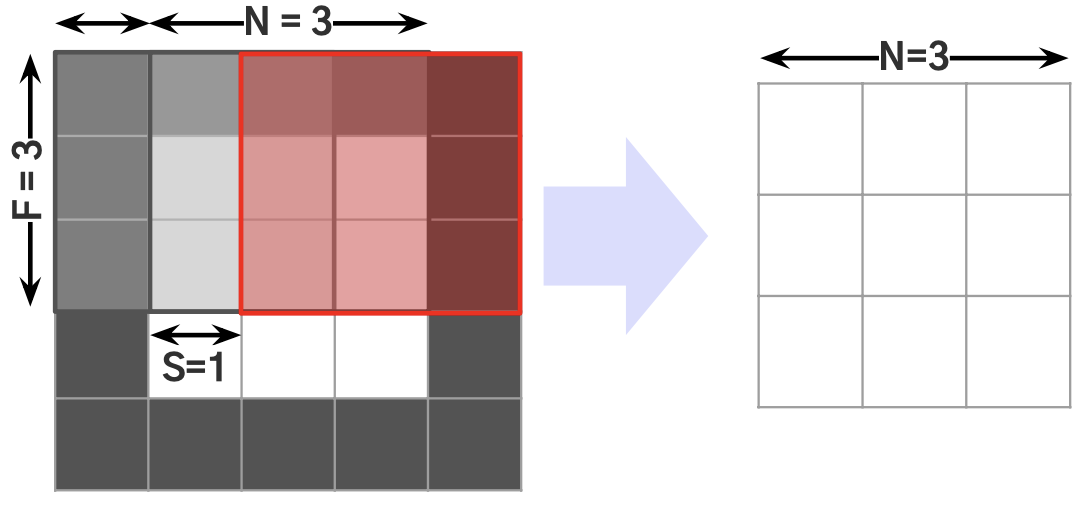
Q. 그럼 Convolution Layer를 거치게 되면 Feature Map의 크기는 무조건 줄어들까?
= Convolution Layer를 무한으로 쌓을 수 없을까? -> 쌓을 수 있음 패딩 이용
- Padding(P): Feature Map의 크기를 일정 수준으로 유지하기 위해서 임의의 값을 넣은 Pixel을 얼마나 추가했는지를 나타냄
- Zero Padding: 0으로 채운 Pixel을 주변에 채워 넣는 것
Activation Function
모델이 비선형성을 가질 수 있도록 만들어 줌
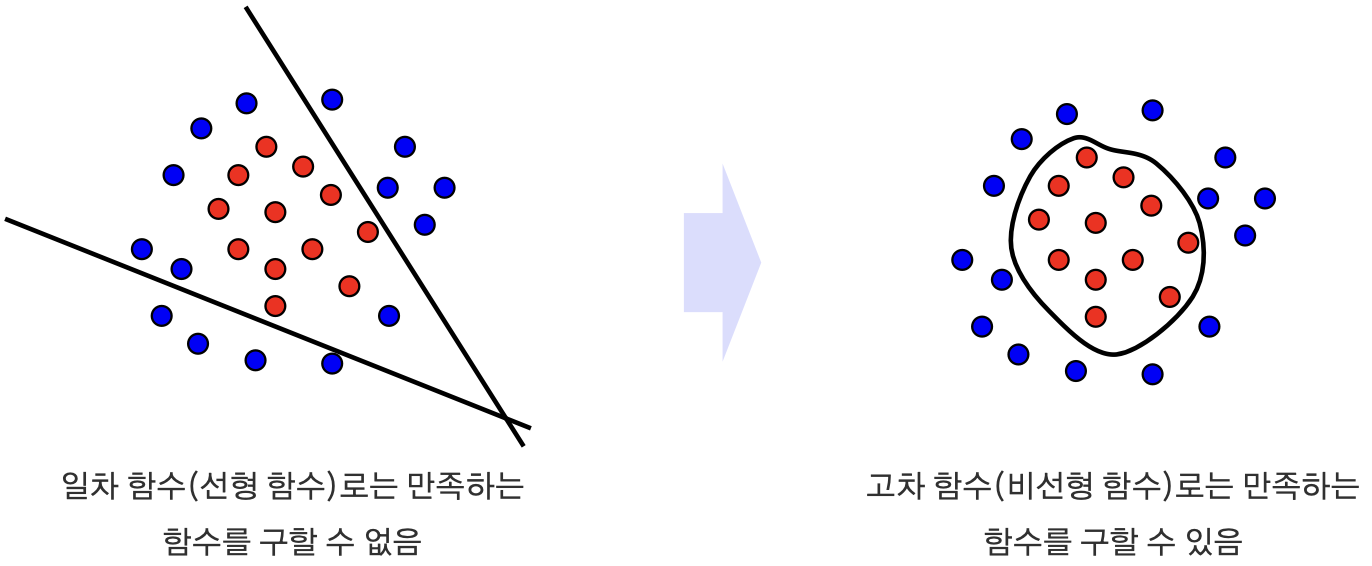
Q. Convolution 연산만 있는 경우는 어떨까?
→ Convolution 연산 결과 1차 함수를 얻게 되므로, Convolution Layer만으로는 선형적인 모델만 만들 수 있게 됨
→ 따라서 Convolution 연산을 거친 뒤 비선형성을 지닌 함수(=Activation Function)를 통과시켜준다면, 복잡한 문제도 풀 수 있는 고차 함수 모델을 만들 수 있게 됨
Pooling Layer
Feature Map에 Spatial Aggregation(공간 집계?)을 시켜줌
-> 다운 샘플링 작업 수행(파라미터를 사용하지 않고도)
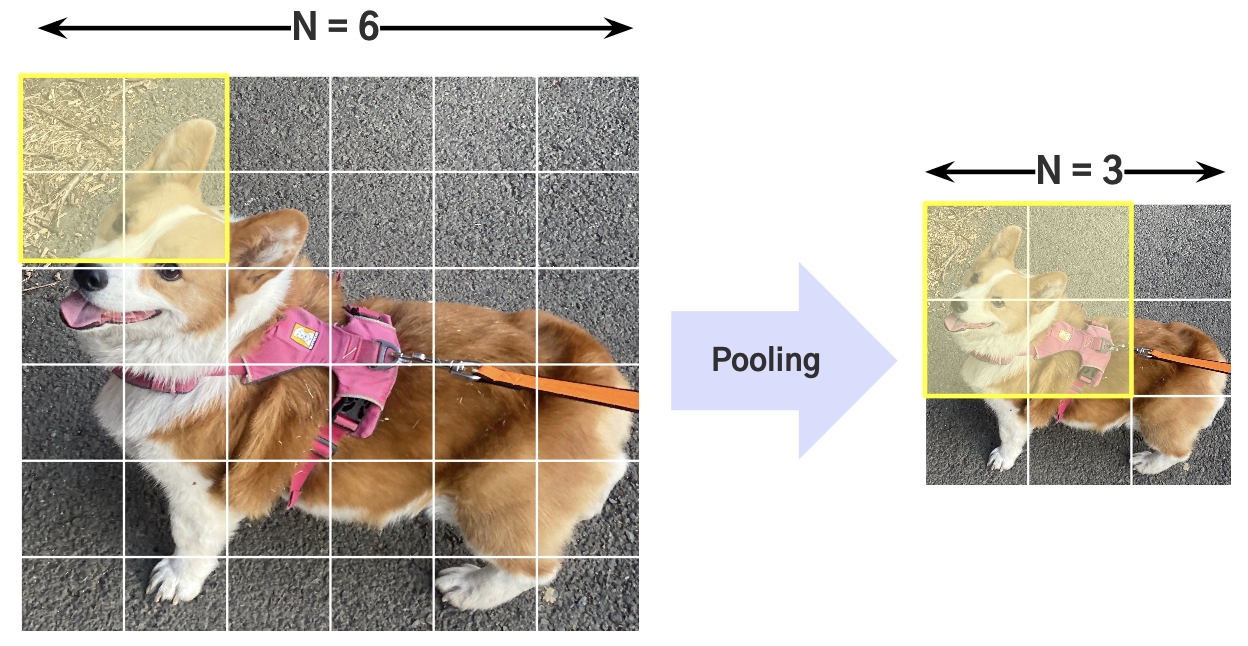
feature map이 줄어들었을 때의 장점.
1. 모델의 파라미터 수 감소
2. Receptive Field(특정 뉴런이 입력 데이터에서 어떤 영역을 '보는' 것)가 달라지게 된다
- 입력 데이터의 공간적인 정보를 줄이고, 계산량을 감소시키며, 학습 파라미터 수를 줄이는 데 도움
- 따라서 풀링 레이어가 있으면, 뉴런의 수용 영역이 줄어들게 되며, 이는 공간적인 정보의 감소와 모델의 계산 효율성을 높이는데 기여
