DAFormer 논문 리뷰

김태훈·2023년 11월 24일

Computer Vision Deep Learning UDA ViT paper-review segmentation

본 페이지에서는 DAFormer: Improving Network Architectures and Training Strategies for Domain-Adaptive Semantic Segmentation 논문에 대해서 말하고자 합니다.

DAFormer 학습 방법에는 DACS의 학습 방법도 사용하였기 때문에 한 번 보시는 걸 추천드립니다.

DACS 논문 리뷰

1. Intro

Semantic Segmentation 분야에서 라벨링에서 발생하는 비용이 너무 커 많은 Unsupervised Domain Adaptation(UDA) 방법론들이 등장했습니다.

그러나 본 논문 이전의 UDA 방법론들에서 사용하는 모델은 CNN기반의 DeepLab V2와 같이 오래된 모델을 사용하였습니다.

그나마 좋은 성능을 내던 DeepLabV2+ResNet101 구조는 지도 학습에서 mIoU가 65정도 되지만 최근 모델 구조들의 mIoU는 거의 85 이상의 성능을 냅니다.

이러한 성능 차이는 UDA 성능을 제대로 발휘하지 못하게 하며 Benchmark Guide에서도 문제가 될 것이라고 합니다.

그래서 본 논문은 비교적 최신구조의 Transformer Encoder를 사용하고 Decoder의 구조를 UDA에 맞게 변경합니다.

추가적으로 간단하지만 중요한 세가지 방법으로 UDA 과정에서 Source Domain에 과적합 되는 것을 방지할 수 있습니다.

간단하게 요약하자면 다음과 같습니다.

기존의 논문들과는 다른 최신의 모델 구조 사용
Rare Class Sampling을 통해 UDA 과정에서 흔한 클래스에 편향되지 않도록 함
Thing-Class ImageNet Feature Distance 이라는 Loss함수 추가
ImageNet으로 사전 학습된 모델을 전이학습을 할 때 Learning Rate에 Warm up 스케쥴링 사용

2. Term

본 논문을 이해하시기 전에 용어들이 어떤 것을 의미하는지 확인하시면 편하실 겁니다.

$N_s$ : Source 데이터들의 개수 입니다.
$N_t$ : Target 데이터들의 개수 입니다.
$X_S = \left\{{x^{(i)}_S}\right\}^{N_S}_{i=1}$ : Source 이미지들을 의미하며 $x^{(i)}_S$ 은 $i$ 번째 Source 이미지 입니다.
$Y_S = \left\{{y^{(i)}_S}\right\}^{N_S}_{i=1}$ : Source 라벨들을 의미하며 $y^{(i)}_S$ 은 $i$ 번째 Source 라벨 입니다.
$X_T = \left\{{x^{(i)}_T}\right\}^{N_T}_{i=1}$ : Target 이미지들을 의미하며 $x^{(i)}_T$ 은 $i$ 번째 Target 이미지 입니다.
$\theta$ : Student Model의 가중치를 의미합니다.
$\phi$ : Teacher Model의 가중치를 의미합니다.
$g_{\theta}$ : Student Model을 의미합니다.
$h_{\phi}$ : Teacher Model을 의미합니다.

3 Self-Training (ST) for UDA

Student Model Weight Update

일반적으로 Source Domain에서 $g_{\theta}$ 를 학습시키기 위해서는 Categorical Cross Entropy를 사용합니다.

그 식은 다음과 같습니다.

L^{(i)}_{S} = - \sum^{H \times W}_{j=1} \sum^{C}_{c=1} y^{(i,j,c)}_{S} \log g_{\theta}(x^{(i)}_{S})^{(j,c)}

이렇게 학습을 진행한 모델은 Target Domain에서는 좋은 성능을 내지 못하는 경우가 많습니다.

그 이유는 Domain Gap 때문이라고 할 수 있습니다.

그러한 Domain Gap을 해결하기 위해서 그동안은 다음과 같은 방법을 사용했습니다.

Adversarial Training
Self Training

그러나 Adversarial Training 기법은 안정적으로 학습하지 못하고 당시에는 Self Training 기법이 더 좋은 성능을 내기 때문에 본 논문에서는 Self Training을 사용합니다.

Self Training에서는 Teacher Model $h_{\phi}$ 를 에 Target 이미지를 입력으로 넣어 클래스에 대한 확률맵을 가진 Pseudo Label을 생성합니다.

이 Pseudo Label을 다음과 같은 Loss 함수에 사용합니다.

L^{(i)}_{T} = - \sum^{H \times W}_{j=1} \sum^{C}_{c=1} q^{(i)}_Tp^{(i,j,c)}_{T} \log g_{\theta}(x^{(i)}_{T})^{(j,c)}

이때 $p^{(i,j,c)}_{T}$ 와 $q^{(i)}_T$ 는 다음과 같습니다.( [ ] 는 Iverson bracket 입니다. )

p^{(i,j,c)}_{T} = [c=\underset{c'}{argmax}(h_{\phi}(x^{(i)}_T)^{(j,c')})]

q^{(i)}_T = \frac{\sum^{H}_{j}{\sum^{W}_{k}{[max_{c'}(h_{\phi}(x^{(i)}_T)^{(j,c')} > \tau)}}}{H \times W}

위 수식의 목적을 간단히 설명하면 다음과 같습니다.

$p^{(i,j,c)}_{T}$ : 각 픽셀에 대해서 클래스를 기준으로 Argmax를 적용하며 가장 확률이 높은 클래스로 반환하는 것
$q^{(i)}_T$ : 각 픽셀의 클래스 확률에 대해서 가장 높은 확률값이 임계값 $\tau$ 를 넘는 픽셀의 비율

즉, 모델의 출력에 대해서 임계값을 넘는 비율만큼 Loss를 전파한다는 의미입니다.

Teacher Model Weight Update

Teacher Model $h_{\phi}$ 의 가중치는 Student Model $g_{\theta}$ 와는 다르게 학습을 통해 가중치가 업데이트 되지 않습니다.

본 논문에서 Teacher Model $h_{\phi}$ 의 가중치는 지수이동평균(Exponential Moving Average)[EMA] 을 통해 가중치를 업데이트합니다.

그 식은 다음과 같습니다.

\phi_{t+1} = \alpha\phi_t + (1-\alpha)\theta_t

$t$ 시점의 $\alpha$ 는 다음과 같이 정해집니다.

\alpha = max(\alpha_{max},1 - \frac{1}{t})

특히 Self Training의 경우 다음과 같은 상황에서 학습이 잘 된다고 합니다.

Student Model $g_{\theta}$ 를 학습시킬 때에는 Target 이미지에 데이터 증강을 적용시키는 것이 좋음
Teacher Model에서 Pseudo Label을 생성할 때에는 데이터 증강을 적용하지 않은 Target 이미지를 입력으로 넣는 것이 좋음

또한 DACS 논문에 나온 방법을 따랐으며 이에 Color Jitter, Gaussian blur와 ClassMix 기법을 사용하였습니다.

4. DAFormer Network Architecture

이전의 UDA 방법론들은 CNN기반의 모델 중 오래되었으며 간단한 DeepLabV2를 사용하였습니다.

CNN의 특성상 Transformer에 비해 새로운 도메인을 만나게 되는 경우 오히려 성능이 급감하는 모습을 보입니다.

즉, CNN은 새로운 도메인에 강건하지 못함을 의미합니다.

Transformer가 왜 CNN보다 강건한지에 대해서 논문의 저자들은 다음과 같이 말합니다.

CNN과 Transformer의 Self-Attention 모두 가중합 방식을 사용하는 것은 동일하지만 CNN은 학습된 가중치를 사용해 가중합되어 정적으로 특징을 추출하는 반면에 Transformer는 유사도와 선호도를 기반으로 동적으로 특징을 추출한다.

본 논문의 저자들은 UDA 기법은 강건한 모델일 수록 더 학습이 잘 된다고 생각하였고 이에 따라 CNN 대신 Transformer구조를 사용하였습니다.

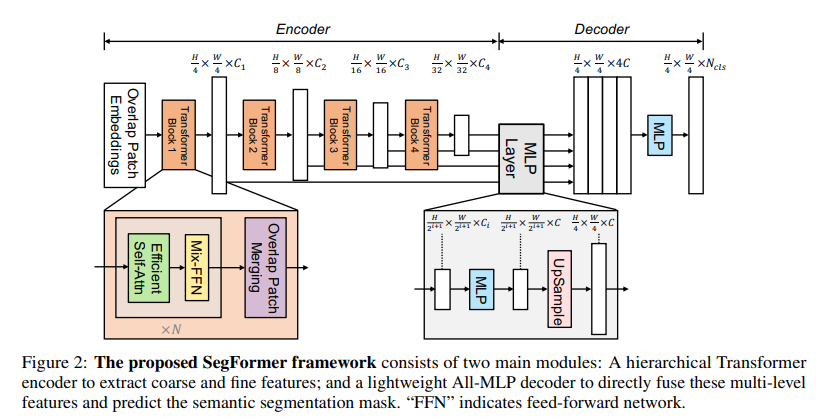
DAFormer의 구조는 SegFormer의 구조를 기반으로 하는 모델입니다.

Encoder

본 논문에서 Encoder로는 SegFormer 논문에 나온 Mix-Transformer(MiT)를 사용하였습니다.

픽셀 단위로 정보를 알아내야하는 Semantic Segmentation에 맞게 고안된 구조
Attention 과정에서 Sequence Reduction을 통해 연산량 감소로 인해 고해상도에서도 괜찮은 성능
여러 층의 특징맵을 만들기 위해 Downsampling 기능을 Patch Merging을 통해 구현하였고 이로 인해 Local Continuity를 유지할 수 있음 (각각의 특징맵은 $F_i \in \R^{\frac{H}{2^{i+1}} \times \frac{W}{2^{i+1}} \times C_i}$ 임)

위의 장점들로 하여 MiT를 Encoder로 사용하였습니다.

Decoder

기존의 SegFormer의 Decoder는 Local Information만을 사용하여 Context 정보가 부족해지게 되었고 이는 강건함을 해치게 되어 UDA에 악영향을 끼치게 됩니다.

이를 해결하기 위해 DAFormer에서는 SegFormer의 Decoder 구조를 수정합니다.

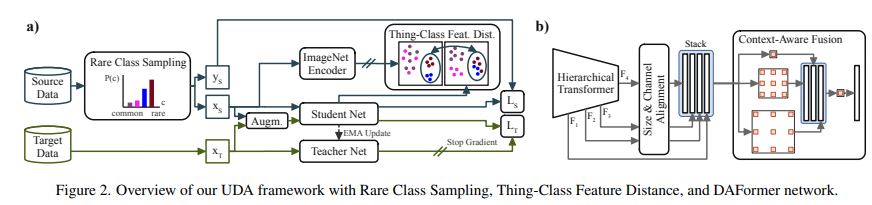
Fig2의 B가 DAFormer의 구조 입니다.

Stack 레이어에서의 기본적인 구조는 SegFormer와 동일하지만 SegFormer보다 적은 수의 채널( $C_e$ )을 사용합니다.

이후 Context Aware Feature Fusion 레이어에서는 ASPP와 비슷하게 서로 다른 Dilation Rates로 $3 \times 3$ Depthwise-Seprable Conv를 적용하여 Concatenate한 뒤 $1 \times 1$ Conv를 적용합니다.

DAFormer와는 다르게 Stack 레이어에서 채널수를 줄였고 Context Aware Feature Fusion에서 Depthwise-Separable Conv를 사용하기 때문에 파라미터의 수를 감소 시켰습니다.

이로 인해 Source Domain으로 과적합될 가능성을 줄였다고 볼 수 있습니다.

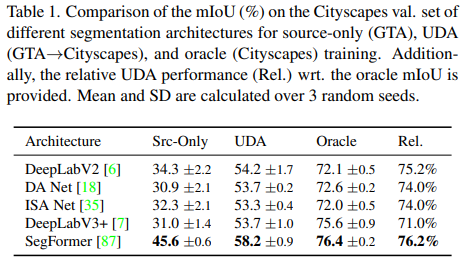
Performance

모델에 따른 성능표

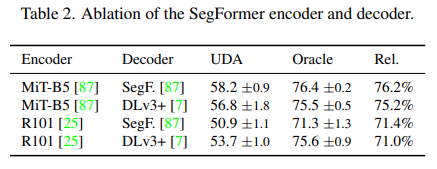
Encoder에 Decoder에 따른 성능표

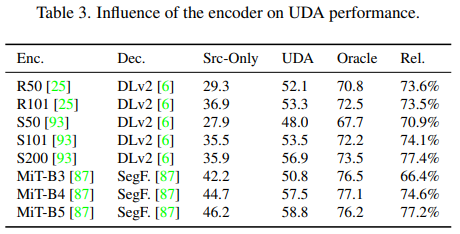
Encoder의 크기에 따른 성능표

5. Training Strategies for UDA

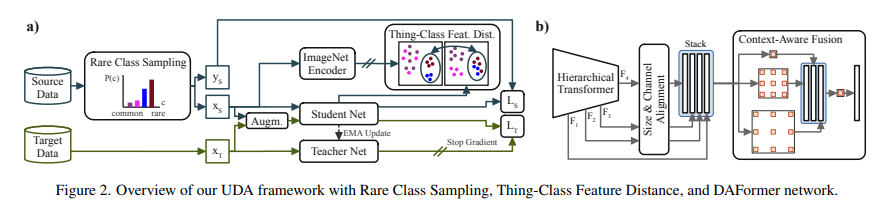
UDA에서 가장 큰 문제점은 Source Domain에 과적합되는 것입니다.

이 문제를 해결하기 위해 학습 방법에 대해서 여러 실험을 하였고 성능을 크게 올렸다고 합니다.

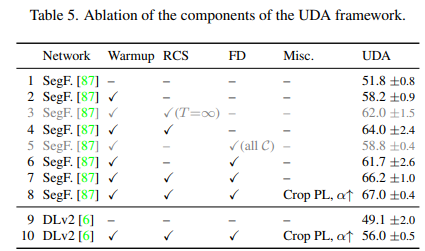
Rare Class Sampling (RCS)

본 논문의 저자들은 흔하지 않은 클래스들에 대한 UDA 성능이 매 학습에 따라 크게 달라지는 것을 확인했다고 합니다.

이 이유는 Random Seed에 따라 흔하지 않은 클래스 속한 이미지가 뽑히는 순서가 다르기 때문입니다.

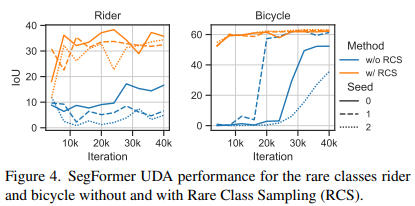
학습 초기에 흔한 클래스가 자주 뽑히고 흔하지 않은 클래스가 뒤에 뽑히게 된다고 가정해봅시다.

모델은 초기에 흔한 클래스를 더 자주 배우게 되어 가중치가 흔한 클래스를 잘 예측하도록 편향되게 됩니다.

이 때문에 이후 흔하지 않은 클래스에 대해 배우려고 할 때 새로 배우기가 어렵습니다.

이는 Self Training에서 더 치명적입니다.

흔하지 않은 클래스에 대해 제대로 배우지 않은 Teacher Model이 생성한 Label로 학습을 진행하게 되면 결국 Student Model은 흔하지 않은 클래스에 대해서 아예 학습하지 못할 수도 있습니다.

이를 해결하기 위해서 흔하지 않은 클래스를 더 자주 뽑도록 합니다.

우선 현재 Source 데이터셋에 있는 라벨에 대해 특정 클래스에 대한 픽셀의 비율을 다음과 같이 계산합니다.

f_c = \frac{\sum^{N_{S}}_{i=1}\sum^{H \times W}_{j=1}[y^{(i,j,c)}_{S}]}{N_{S} \cdot H \cdot W}

비율 $f_c$ 가 낮을 수록 데이터셋에서 클래스 $c$ 의 비율이 낮다는 것입니다.

이후 Sampling 확률 $P(c)$ 에 대해서 다음과 같이 계산합니다.

P(c) = \frac{e^{(1-f_{c})/T}}{\sum^{C}_{c'=1}e^{(1-f_{c'})/T}}

$1-f_{c}$ 로 인해 비율이 낮은 클래스가 더 높은 $P(c)$ 를 갖게 됩니다.

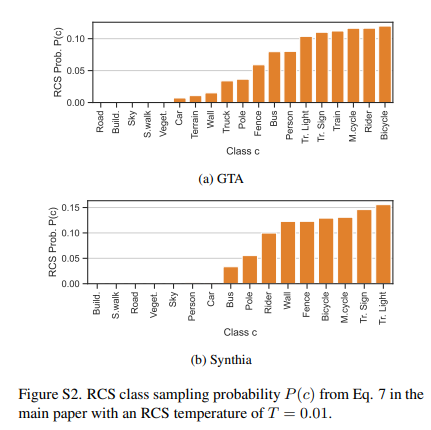
이때 $T$ 는 확률분포 $P(c)$ 의 부드러움을 결정합니다.

$T$ 가 크면 $P(c)$ 의 분포가 균일 분포와 비슷해집니다.

반대로 $T$ 가 작으면 $P(c)$ 의 분포는 흔하지 않은 클래스(작은 $f_c$ )를 더 자주 뽑도록 합니다.

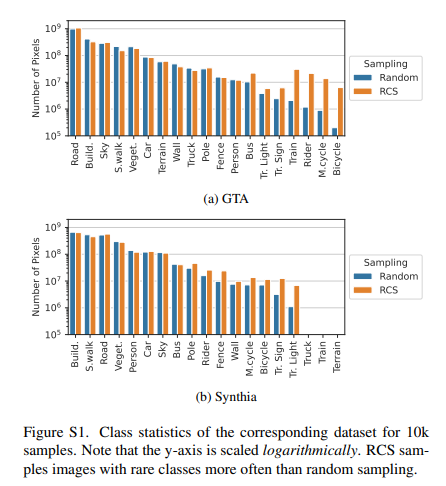
대게 흔하지 않은 클래스(사람, 바이크 등)은 흔한 클래스(도로, 나무, 하늘 등)와 같은 이미지 내에 있을 확률이 높습니다.

이 때문에 흔하지 않은 클래스를 포함한 이미지를 주로 뽑는다고 해도 Sampling 비율은 비슷한 것입니다.

이 Sampling 과정은 다음과 같습니다.

전처리 과정

모든 라벨에 대해서 어떤 라벨에 어떤 클래스가 얼마나 있는지를 정리하여 파일이나 메모리에 저장
각 클래스에 대해서 $f_c$ 를 미리 계산하여 파일이나 메모리에 저장
클래스 별로 해당 클래스를 포함한 라벨에 대한 정보를 파일이나 메모리에 저장

Sampling 과정

미리 구해둔 $f_c$ 를 통해 분포 $P(c)$ 를 계산
분포 $P(c)$ 를 기반으로 확률적으로 클래스를 선택 ( $c$ ~ $P$ )
선택한 클래스가 들어있는 라벨들 중에 하나를 균등분포를 따라 선택함과 동시에 라벨에 맞는 이미지를 같이 불러옴 ( $x_{S}$ ~ uniform( $X_{S,c}$ ))

아래는 하이퍼 파라미터 $T$ 에 따른 성능차이 입니다.

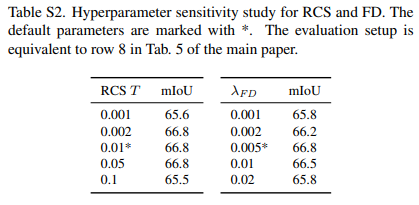
Thing-Class ImageNet Feature Distance (FD)

ImageNet의 데이터셋은 실제로 존재하는 사물들의 정보를 잘 담고 있다고 합니다.

그렇기 때문에 이런 ImageNet을 통해 사전학습을 한 모델은 고수준의 유의미한 의미론적 특징을 추출해낼 수 있습니다.

이런 의미론적 특징을 통해 UDA에서 구분하기 힘든 버스나 기차의 특징도 쉽게 구분할 수 있다고 합니다.

실제로 저자들은 DAFormer를 학습하면서 초기에는 버스나 기차를 잘 분할(Segment)하는 것을 확인할 수 있었지만 나중에는 분할해내지 못하는 것을 확인한다고 합니다.

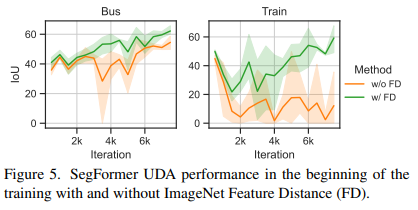
이 이유는 학습 과정에서 ImageNet의 정보를 잃어간다고 판단하였고 또한 Source 데이터에 과적합 되어 간다고 판단하였습니다.

그래서 ImageNet의 정보를 잃지 않게 하기 위해서 모델의 Bottleneck Feature( $F$ )을 활용하여 Feature Distance(FD)를 구합니다.

Feature Distance의 식은 다음과 같습니다.

※ $F_{ImageNet}$ 은 ImageNet으로 사전 학습한 모델의 Bottleneck Feature입니다.

d^{i,j} = || F_{ImageNet}(X^{(i)}_{S})^{(j)} - F_{\theta}(x^{(i)}_{S})^{(j)} ||_{2}

하지만 ImageNet은 도로, 하늘과 같은 배경을 포함한 Stuff-Class가 아닌 주로 차 또는 얼룩말과 같은 Thing-class에 대해서 주로 학습합니다.

그렇기 떄문에 Feature Distance Loss를 Thing-class에 대해서만 학습합니다.

그러기 위해서 $C_{things}$ 와 이진 Mask $M_{things}$ 를 활용합니다.

※ $C_{things}$ 는 Thing-Class의 집합입니다.

클래스 정보가 0 : 하늘, 1 : 도로, 2 : 차 인 경우에 2번 클래스인 차만 Thing-Class이기 때문에 $C_{things}$ 는 다음과 같습니다.

C_{things} = [2]

Thing Class Feature Distance Loss 함수는 다음과 같습니다.

L^{(i)}_{FD} = \frac{\sum^{H_{F} \times W_{F}}_{j=1}d^{(i,j)} \cdot M^{(i,j)}_{things}}{\sum_{j} M^{(i,j)}_{things}}

이 때 $M^{(i,j)}_{things}$ 은 다음과 같이 정의합니다.

M^{(i,j)}_{things} = \sum^{C}_{c'=1}y^{i,j,c'}_{S,small} \cdot [ c' \in C_{things} ]

$y^{(i)}_{S,small}$ 은 라벨 $y^{(i)}_{S}$ 크기를 Average Pooling으로 크기를 $\frac{H}{H_{F}} \times \frac{W}{W_{F}}$ 로 줄인 것입니다.

이후 임계값 $r$ 를 넘으면 1 아니면 0으로 전환하여 이진 Mask로 바꾸어 줍니다.

식은 다음과 같습니다.

y^{c}_{S,small} = [AvgPool(y^{c}_{S},H/H_{F},W/W_{F})>r]

저는 이 부분을 이해할 때 $y^{(i)}_{S}$ 가 Bottleneck Feature Map을 의미하는 것으로 잘못 이해하고 구현하려 하다가 어떤 채널이 어떤 클래스와 연관된 거지 하며 한동안 이해하지 못하고 있었습니다...

간단하게 과정을 설명하면 다음과 같습니다.

Bottleneck Feature Map과 $y^{(i)}_{S}$ 의 해상도를 통해 $H_{F},W_{F}$ 를 구합니다.

이후에 $L^{(i)}_{FD}$ 를 구할 때 해상도를 맞춰주기 위함입니다.
$y^{(i)}_{S}$ 에 AvgPool을 적용하여 해상도를 줄여줍니다.

Shape( $H \times W \times C$ -> $\frac{H}{H_{F}} \times \frac{W}{W_{F}} \times C$ )

패치단위로 크기를 줄이게 되므로 AvgPool 을 적용한 결과의 한 픽셀은 $H_{F} \times W_{F}$ 범위 내의 클래스 비율의 정보를 담고 있습니다.
임계값 $r$ 을 기준으로 1과 0으로 구분하여 이진화 하여 $y^{(i)}_{S,small}$ 을 완성합니다.

Shape( $\frac{H}{H_{F}} \times \frac{W}{W_{F}} \times C$ )

해당 패치 내부에 특정 클래스 개수의 비율이 $r$ 을 초과하면 1이고 아니면 0이 됩니다.
$y^{(i)}_{S,small}$ 의 각 클래스 채널에 대해서 해당 클래스가 Thing-class에 속하는 경우에 해당 채널에는 1 나머지에는 0을 곱해주고 채널 축으로 전부 더해주어 $M^{(i,j)}_{things}$ 을 만들어줍니다.

Shape( $\frac{H}{H_{F}} \times \frac{W}{W_{F}} \times C$ -> $\frac{H}{H_{F}} \times \frac{W}{W_{F}}$ )

$M^{(i,j)}_{things}$ 의 각 픽셀의 의미는 다음과 같습니다.

해당 패치내에 존재하는 클래스들의 비율이 $r$ 보다 큰 클래스들 중에서 Thing-class에 속하는 클래스의 갯수를 의미합니다.
$d^{(i,j)}$ 를 구하기 위해 두 Bottleneck Feature의 차이를 구하고 채널 축으로 2 Norm을 구합니다.

Shape( $\frac{H}{H_{F}} \times \frac{W}{W_{F}} \times C$ -> $\frac{H}{H_{F}} \times \frac{W}{W_{F}}$ )
$d^{(i,j)}$ 와 $M^{(i,j)}_{things}$ 를 이용해 $L^{(i)}_{FD}$ 를 구합니다.

Shape( $\frac{H}{H_{F}} \times \frac{W}{W_{F}}$ -> 1)

결국 하나의 Scalar 값이 나오게 되어 Loss로 계산이 가능하게 됩니다.

$L_{FD}$ 까지 사용하여 본 논문에서 사용하는 최종적인 Loss함수는 다음과 같습니다.

L^{(i)} = L^{(i)}_{S} + L^{(i)}_{T} + \lambda_{FD}L^{(i)}_{FD}

Learning Rate Warmup for UDA

선형적으로 학습률을 높이는 방법은 CNN과 Transformer 두 구조에서 모두 좋은 성능을 냈습니다.

Warmup 스케쥴링은 학습 초기에 큰 학습률이 Gradient 분포를 왜곡하는 것을 방지하면서 모델의 일반화 능력을 키워줍니다.

특히 이 Warmup 스케쥴링은 작은 학습률에서 시작하기 때문에 사전학습된 이미지 넷의 특징을 최대한 유지하기 때문에 Real World Domain의 정보를 유지할 수 있어 좋은 성능을 낼 수 있습니다.

$t$ 시점의 학습률은 다음과 같이 설정됩니다.

lr_t = lr_{base} \cdot t/t_{warmup}

6. 마무리

UDA 과정에서 강건함의 문제를 인식하고 Transformer 계열을 시도하면서 UDA 맞게 모델 구조를 변경함으로 모델의 연산량을 줄이며 강건함을 키웠다는 점이 하나의 돌파구가 되었다고 생각합니다.

특히 모델 구조 뿐만 아니라 Class-Imbalance로 인한 성능 문제와 ImageNet 특징 활용 등에서 여러 성능 분석을 진행한 모습이 인상 깊었으며 이 실험을 하는 저자들의 노력이 대단함을 볼 수 있었습니다.

이후 MIC라는 논문과도 연관이 있으니 이해하고 가시면 좋을 듯 합니다.

김태훈

👋 인공지능을 통해 다음 세대가 더 나은 삶을 살도록

이전 포스트

DACS 논문 리뷰

다음 포스트