Intro

Machine Learning Data Flow Process

Problem Exploration - Data Engineering - Model Engineering - ML Ops

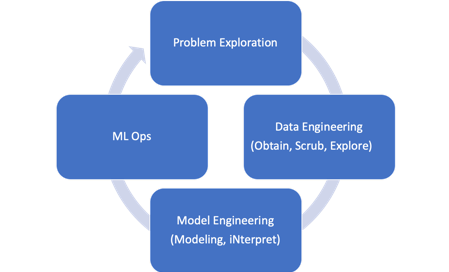
(참고) ML Ops : 계속해서 데이터가 다시 들어오는 경우, 모델을 지속적으로 다시 학습시키는 운영방법론
(참고2) ML에 필요한 데이터는 1만, DL에 필요한 데이터는 10만 order 수준이라고 함

Python Machine Learning Package - Scikit learn

Python Open-source package for maching learning modeling
Not only provide various machine learning models, But also Preprocessing, Score, Managing method.
https://scikit-learn.org/stable/

Linear Regression

Linear Regression은 예측을 위한 지도학습 머신 러닝
Supervised Learning의 일종이기 때문에 데이터가 연속형일 경우 사용 할 수 있다.

Simple Linear Regression

설명변수(x)를 하나만 사용하는 Linear Regression

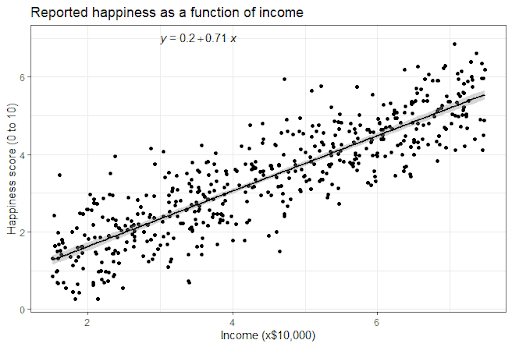
기본 구조

$y_i = \beta_0+\beta_1x_i+\varepsilon_i$
$y_i = \hat{y}+\varepsilon_i$

비용 함수 cost function

Linear Regression 기본 구조를 만드는 $\beta$ 계수 값들을 어떻게 찾을 수 있을까?
당연히 오차를 최소로 만드는 방향으로 모델링을 하고 싶을 것
회귀 모델은 일반적으로 최소자승법(least square method를 사용해서 오차의 제곱합을 최소화 하는 방향으로 계수를 결정한다

$cost = {1\over2n} \sum_i^n{(y_i - \hat y_i)^2}$

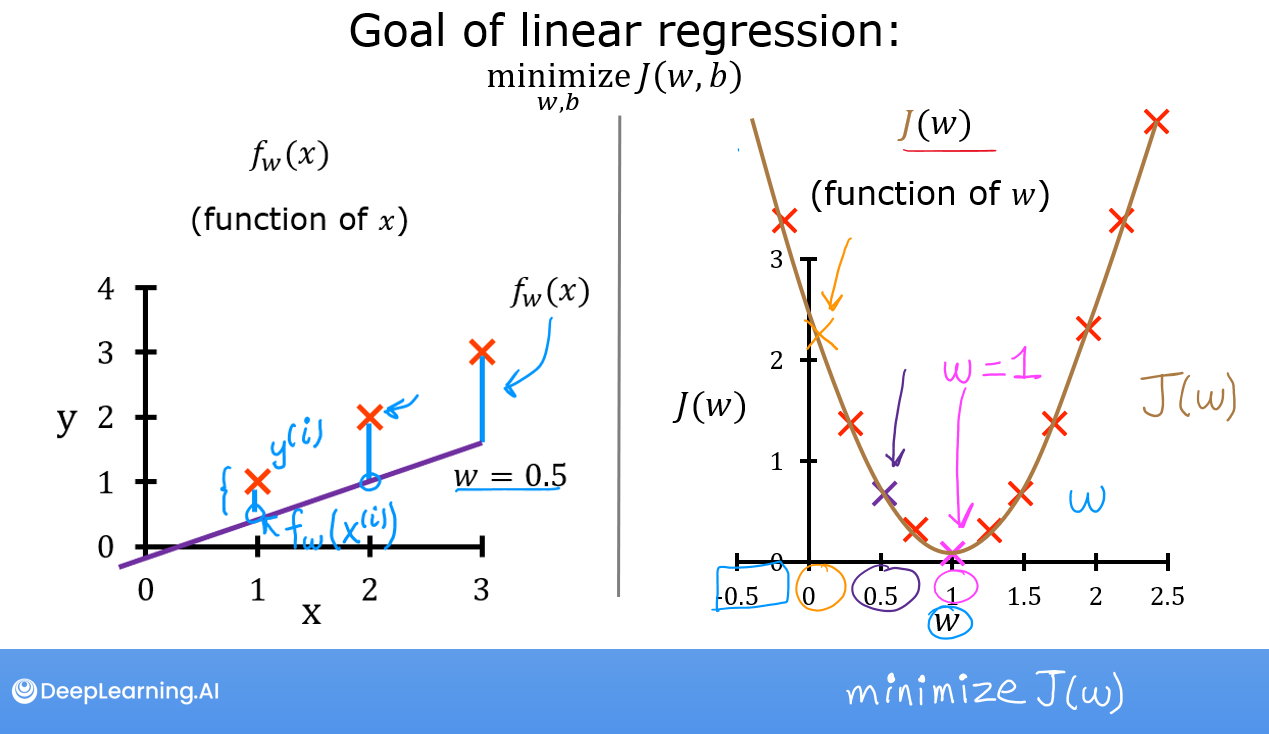
비용 함수의 최소값을 찾기 위해 미분을 통해 기울기가 0인 지점을 찾아내는 방법을 경사하강법(gradient decent)라고 한다.
미분 값과 반대방향으로 움직이면서 비용함수의 최소값에 다다르게 되는 것

Linear Regression의 평가

모델의 예측력과 모델의 설명력을 평가한다

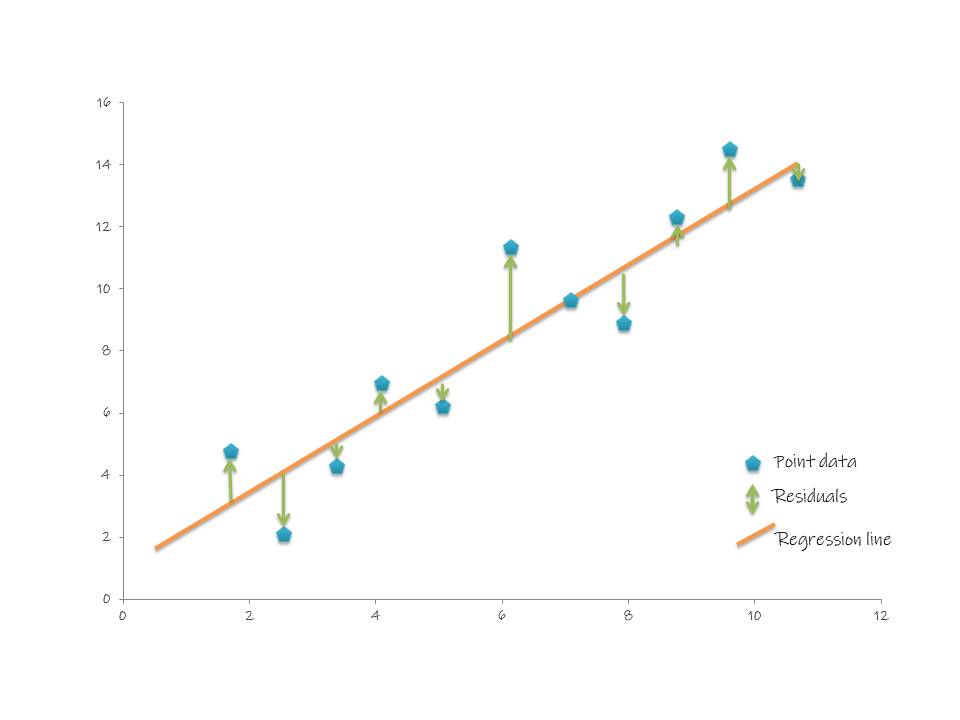
• 예측력 -> RMSE
  Root Mean Squared Error 평균 제곱 오차의 제곱근
  예측모델에서 가장 많이 쓰이는 오차로 예측이 평균적으로 RMSE만큼 오차가 난다 라고 설명할 수 있음. 즉, 이 모델이 sample들을 얼마나 잘 예측하고 있는가? 라고 말해 볼 수 있음.
  $\sqrt{{1\over n}\sum_i^n(y_i-\hat{y_i})^2}$

  

• 설명력 -> R2 Score
  결정계수(Coefficient of determination) 혹은 설명계수
  독립변수(feature x)들이 종속변수(label y)를 얼마나 잘 설명하는가에 대한 설명력에 대한 평가지표
  일반적으로 R2 score가 0.6 이상이여야 사용 가능한 모델이라고 해석한다
  $SST(Sum\ of\ Squared\ of\ Total) = \sum(y_i-\bar{y})^2$
  $SSR(Sum\ of\ Squared\ due\ to\ Regression) = \sum(\hat{y_i}-\bar{y})^2$ : 모델이 설명할 수 있는 변동
  $SSE(Sum\ of\ Squared\ of\ Error) = \sum(y_i-\hat{y})^2$ : 모델이 설명할 수 없는 변동
  $R^2 = 1-{SSE \over SST} = {SSR \over SST} = {선형 모형의 오차 \over 전체 오차}$
  
  

Multiple Linear Regression

독립변수가 두 개 이상인 가장 일반적인 형태의 선형 회귀 모델

기본 구조

$y_i = \beta_0 + \beta_1 x_{i,1} + \beta_2 x_{i,2} + \cdots + \beta_p x_{i,p} + \varepsilon_i$

행렬로 표현하면 아래와 같음

$y=X\beta+\varepsilon$

$y = \begin{pmatrix} y_1 \\ y_2 \\ \vdots \\ y_n\end{pmatrix}$

$X = \begin{pmatrix} 1 & x_{1,1} & \dots & x_{1,p} \\ 1 & x_{2,1} & \dots & x_{2,p} \\ \vdots & \vdots & \ddots & \vdots \\ 1 & x_{n,1} & \dots & x_{n,p}\end{pmatrix}$

$\beta = \begin{pmatrix} \beta_0 \\ \beta_1 \\ \vdots \\ \beta_p\end{pmatrix}$

$\varepsilon = \begin{pmatrix} \varepsilon_0 \\ \varepsilon_1 \\ \vdots \\ \varepsilon_n\end{pmatrix}$

비용 함수

Simple Linear Regression Model과 마찬가지로 Least Squre Method를 사용함

$\varepsilon = y - \hat{y}$
$\hat{y} = X\beta$

${\partial J \over \partial \beta} = 0 \Rightarrow \beta = (X^TX)^{-1}X^Ty$

참고

Code

# module import
from pandas as pd
from sklearn.linear_model import LinearRegression

# data load
df = pd.read_csv('./data/data_name.csv')
X = df['feature']
y = df['y']

# split Train - Test
from sklearn.model_selection import train_test_split
X_train, X_test, y_train, y_test = train_test_split(X,y, test_size =0.3, random_state = 42)

# modeling
lr = LinearRegression()
lr.fit(X_train, y_train)
y_pred = lr.predict(X_test)

# check model coefficient
lr.intercept_, lr.coef_ #beta0, beta1~beta(len(X.columns()))

#

# assessment
from sklearn.metrics import r2_score, mean_squared_error
print(f'r2_score : {r2_score(y_test, y_pred)}')
print(f'RMSE : {mean_squred_error(y_test, y_pred)**0.5}')

정규화 모델 (Regularized Model)

overfitting

모델이 일반화가 안되어 학습한 모델에 대한 데이터 예측 성능은 높지만, 테스트 데이터 예측 성능이 떨어지는 경우
모델이 복잡해질수록 과적합 될 수 있음

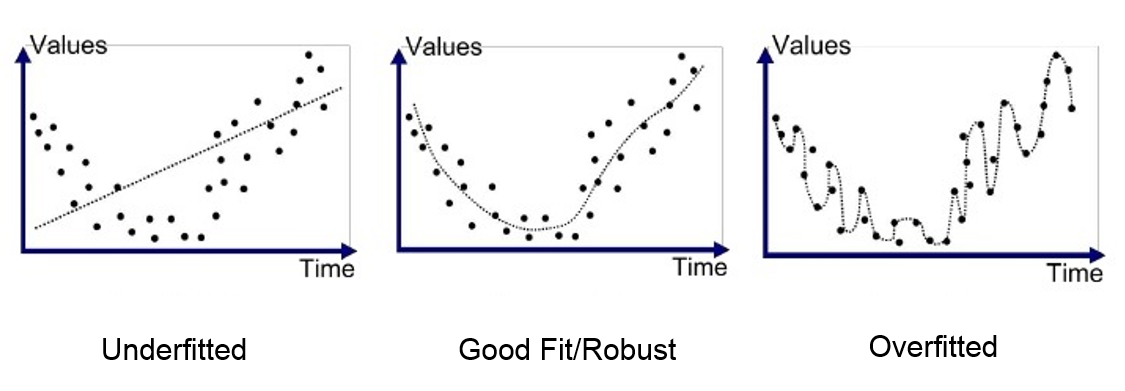
일반적으로 샘플의 수가 변수의 개수 대비 충분하지 않는 경우 회귀모델은 과적합 될 수 있는데, 회귀 모델은 큰 관계가 없는 변수를 없애주지는 모함. 이를 해결하기 위해 설명변수 X가 너무 많으면 정규화(규제)를 통해 이를 해결함

Lasso Model

설명 변수의 beta 절대값의 합을 패널티로 추가함

$J = \sum^n_{i=1}(y_i-\hat{y_i})^2 + \lambda\sum^p_{j=1}\left\vert\beta_j\right\vert$
$n = sample\ 갯수$
$p = 설명변수\ 갯수$

모델이 loss function을 최소화 하는 과정에서
회귀모델의 오차와 베타 절대값의 합을 동시에 최소화 시키는 방법으로 학습을 진행함

베타의 절대값을 줄이는 과정에서 회귀계수 베타의 값을 0으로 만들어 가기 때문에 변수 자체를 줄일 수 있음

참고

Code

from sklearn.linear_model import Lasso
my_ls = Lasso(alpha = 1)

Ridge Model

Code

from sklearn.linear_model import Ridge
my_ls = Ridge()

Polynomial model

변수 간 영향력에 해당하는 새로운 변수를 생성하여 비선형으로 만들고 선형모델로 저장
보통 2차원 3차원까지 적용하기 때문에, 변수가 많아지므로 Ridge,Lasso 정규화 모델을 적용한다

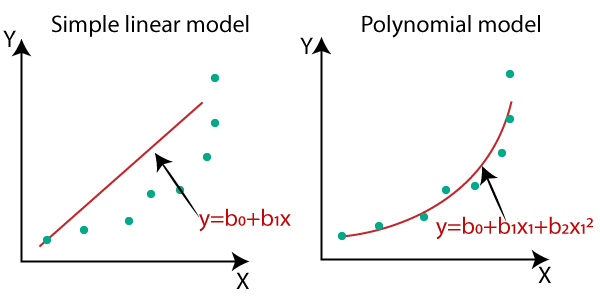
Code

# model import
from sklearn.preprocessing import PolynomialFeatures

# polynomial maker instance
poly = PolynomialFeatures(degree = 2, include_bias=False)

'''
degree=2 : 차수설정
include_bias=False : 상수항 제거(필수)
'''

# set polynomial features
poly.fit(X_train)
poly_X_train = pd.DataFrame(poly.transform(X_train), columns = poly.get_feature_names_out())
poly_X_test = poly.transform(X_test)

Logistic Regression

logistic Regression은 분류를 위한 지도학습 머신러닝 모델

종속변수가 Binary Distribution을 보일 경우, 기존 선형 모델로는 해결이 어려움.

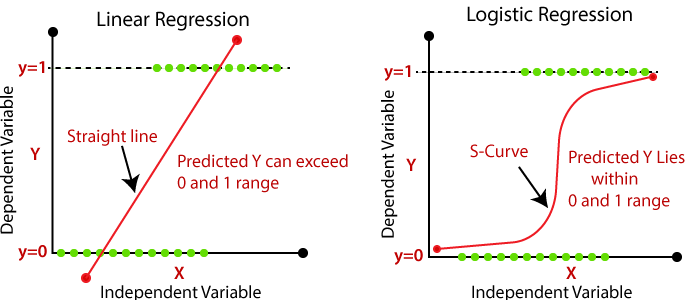
이를 해결하기 위해 모델의 출력 결과를 0과 1사이에 놓일 수 있도록 모델링 한 것
즉, 확률 문제로 접근해서 분류 문제에 사용 가능하겠다는 아이디어로 시작된 것

데이터가 많을 수록 퍼포먼스가 떨어진다는 단점이 있음
왜냐면 0.5 근처에서 완벽하게 구별할 수 없는 문제가 있기 때문
그래서 최근 분류 모델은 Deep Learning으로 많이 가고 있는 추세이긴 함

Odds(승산비)

$p : 어떤\ 일이\ 발생할\ 확률\ (승산)$

$Odds = {p \over {1-p}} : \ 어떤\ 일이\ 발생할\ 확률\ / 발생하지\ 않을\ 확률\ (승산비)$

$p$는 확률이니까 0과 1 사이의 값이고
$p$가 0에 가까울 경우 $Odds$는 0
$p$가 1에 가까울 경우 $Odds$는 무한대

때문에 여기서 log를 취하면 0을 기준으로 상호 대칭적인 식이 완성됩니다.

$log({Y \over {1-Y}}) = \beta_0 + \beta_1x$

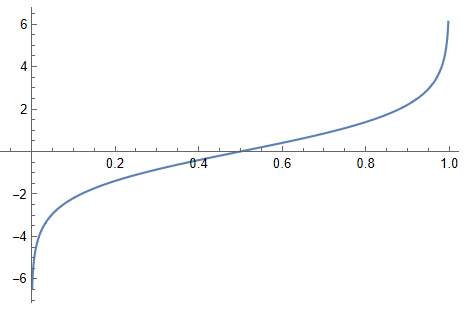
이를 다시 y에 대해 정리하면 sigmoid 식이 됩니다.

$y = {1 \over {1+\exp^{-(\beta_0 + \beta_1x)}}}$

$0<sigmoid(x)<1$
$sigmoid(0)=0.5$
이 값을 확률값 처럼 생각해 볼 수 있음

$\hat{y} = \begin{cases} 1 & \text{ if } \ h(x) \geq 0.5 \\ 0 & \text{ if } \ h(x) < 0.5 \end{cases}$

비용 함수

그럼 logistic 회귀 분석은 어떤 비용함수를 가질까?
분류형태의 경우 비용함수를 어떻게 설정해야 할까?

먼저 y값(real label)이 1과 0을 가지는 binary 문제를 생각했을 때,
값이 1이라면 그때의 확률은 1
값이 0이라면 그때의 확률은 0
이렇게 분류하는 것이 가장 정확하다

근데 값이 1인데 내가 확률을 0.8로 했을 때랑
내가 확률을 0.6이라고 했을 때, cost차이가 훨씬 커야한다
그리고 특히 값이 0인데 내가 확률을 1이라고 했을때 아주 큰 패널티(cost를 무한으로!)를 주어야 한다

$cost(h(x), y) = -ylog(h(x)) - (1-y)log(1-h(x))$

https://wikidocs.net/4289

Classification Model의 평가

오차행렬(confusion matrix)와 분류평가표(classification report)를 사용하여 모델을 평가함

오차행렬 Confusion Matrix

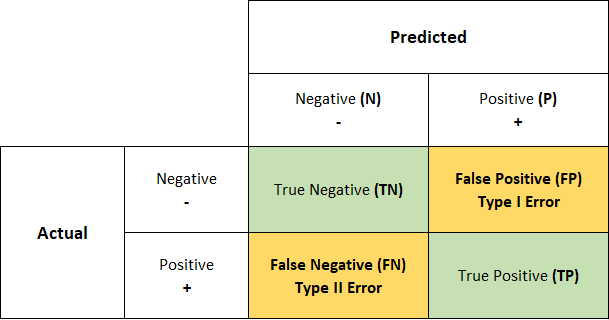
<명명규칙>
모델 예측이 맞으면 T(rue)
모델 예측이 틀리면 F(alse)
모델 예측값이 N(egative)
모델 예측값이 P(ositive) - 중점적으로 봐야 하는 값(1), detecting하려는 대상

FP - 가성 불량
FN - 미검출 불량

정확도(Accuracy) : 맞춘 비율

${{TN+TP}\over{TN+FP+FN+TP}}$

정밀도(Precision) : Detecting한 값들은 얼마나 잘 맞췄는지

${{TP}\over{TP+FP}}$

재현율(Recall) : 실제 Detecting해야 하는 값 중 얼마나 잘 찾았는지

${{TP}\over{TP+FN}}$

f1-score : precision과 recall의 조화 평균

${{2*precision*recall}\over{precision+recall}}$

상황에 따라 어떤 값을 예민하게 보아야 하는지 확인해 볼 수 있음
예) 제품 생산 불량
일반적으로 미검출 불량(FN)에 기업은 가장 민감함
즉, 재현율을 민감하게 보아야 함.
예2) 스마트폰 지문인식
다른 사람이 지문인식을 했을 때 되는 경우를 Detecting 해야하는 것으로 보았을 때,
실제 다른 사람이 지문인식을 했는데 내가 했다고 판단하는 경우는 보안(=FN),
내가 인식했는데 다른 사람이 했다고 판단하는 경우는 인식률(=FP)
이런 경우는 어떤 값이 중요한지 판단할 필요가 생김
이렇게 둘다 잡아야 하는 경우 f1-score를 높여야 함.

분류 평가표 Classification Report

Code

# module import
from sklearn.linear_model import LogisticRegression
# data load
from sklearn.datasets import load_breast_cancer
cancer = load_breast_cancer()

# check data
print(cancer['DESCR'])
# make DataFrame
import pandas as pd
X = pd.DataFrame(cancer['data'], columns = cancer['feature_names'])
y = pd.DataFrame(cancer['target'])

# Inverse Target Value
y = abs(cancer['target']-1)

# split Train - Test Data
from sklearn.model_selection import train_test_split
# make "stratify = label"
X_train, X_test, y_train, y_test = train_test_split(X,y, test_size=0.3, random_state=42, stratify=y)

# modeling
lr = LogisticRegression()
lr.fit(X_train,y_train)
y_pred = lr.predict(X_test)
# check predict_probability
lr.predict_proba(X_test)

# model assessment
from sklearn.metrics import confusion_matrix, classification_report
print(confusion_matrix(y_test, y_pred))
print(classification_report(y_test, y_pred))

LogisticRegression Options

LogisticRegression(
penalty = 'l1', #기본설정은 ridge(l2), l1은 lasso
C = 1.0, #lambda값으로 규제화 정도 의미
random_state = 42, #난수 설정 초기값, 결과값 fix됨
solver = 'lbfgs'
)

multi로 분류를 할 때, 일부 최적화 방법이 고정되어 있음

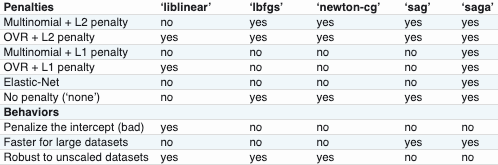
Tree base model

Decision Tree(CART : Classification and Regression Tree)

Decision Tree는 예측/분류가 모두 가능한 지도학습 머신러닝 모델
스무고개 게임을 하듯 여러 가정을 데이터에 반영하고 이를 바탕으로 decision boundary(결정 경계)를 생성한다.

또한, 스무고개 처럼 진행하기 때문에 결과 해석이 굉장히 용이하기 때문에 모델 해석이 필요한 문제에 주로 사용된다. (ex. 신용평가)
최근에는, decision tree를 베이스로 한 부스팅 트리 모델(Xgboost, LightGBM, Catboost) 등으로 확장판 모델들이 많이 개발되었다.

모델 구조

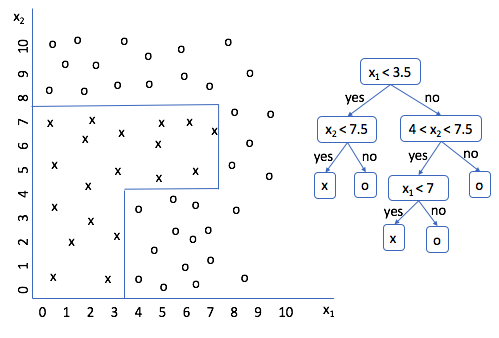
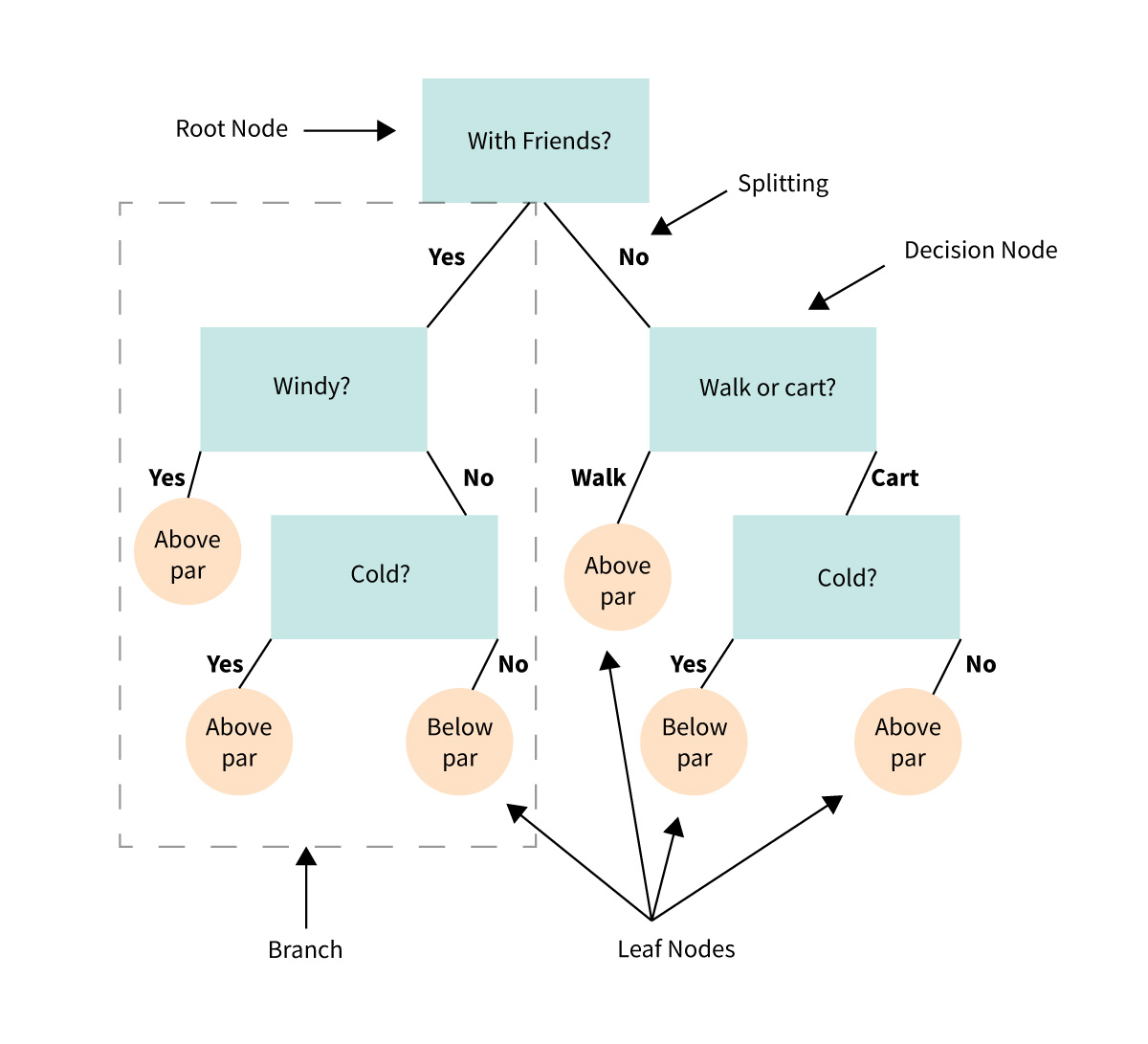
Root Node : 최상위 노드
Leaf Node : 최하위 노드
Branch : 노드를 나누는 기준
Root Node - Leaf Nodes 까지 Node 갯수 : Depth (모델의 복잡도을 의미)

더이상 나눌 수 없을 때 까지 확장을 함.
즉, 학습 DATA의 정답률이 100% 될 때 까지 학습을 함 -> overfitting

불순도 Impurity

Decision Tree를 학습시키는 방법
정보화 이론에서 사용하는 Gini 계수와 entropy를 사용한다
0.5에 가까울 수록 불순도가 높고,
0 또는 1에 가까울수록 순도가 높다고 볼 수 있다

$Gini = 1 - \sum_1^n{(p_i)^2}$

$Entropy = - \sum_1^n{p_iln(p_i)}$

즉, 한 노드의 불순도가 가능한 많이 떨어지도록 노드를 나눈다.
그러니까 Gini Index가 0이 될때 까지 학습을 시키는 것

그럼 어떤 라인을 그리는것이 가장 좋을까?
어떻게 decision boundary를 긋는 것이 가장 나은 선택일까?
이것이 greedy 알고리즘

Code

# load data
from sklearn.datasets import load_iris
# check data
iris = load_iris()
print(iris['DESCR'])
# make dataFrame
import pandas as pd
X = pd.DataFrame(iris['data'], columns = iris['feature_names'])
y = iris['target']

# split train - test
from sklearn.model_selection import train_test_split
X_train, X_test, y_train, y_test = train_test_split(X, y)

# modeling
from sklearn.tree import DecisionTreeClassifier
dtc = DecisionTreeClassifier(random_state=42)
dtc.fit(X_train,y_train)
y_pred = dtc.predict(X_test)

# model_score
from sklearn.metrics import classification_report, confusion_matrix
print(confusion_matrix(y_test, y_pred))
print(classification_report(y_test, y_pred, target_names = iris['target_names']))

[[ 9  0  0]
 [ 0 15  3]
 [ 0  3  8]]
              precision    recall  f1-score   support

      setosa       1.00      1.00      1.00         9
  versicolor       0.83      0.83      0.83        18
   virginica       0.73      0.73      0.73        11

    accuracy                           0.84        38
   macro avg       0.85      0.85      0.85        38
weighted avg       0.84      0.84      0.84        38

데이터 분포

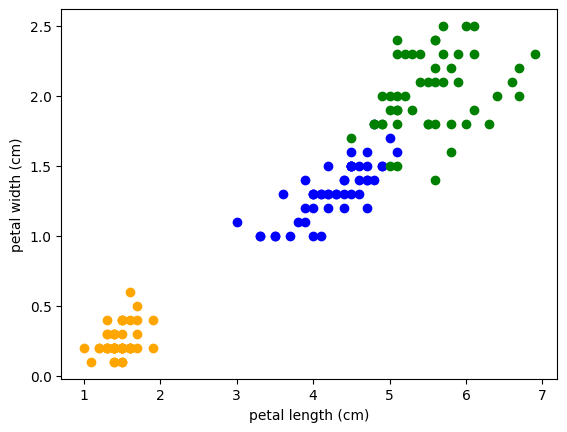
코드의 설명력을 시각화 하는 방법

# feature importance
import matplotlib.pyplot as plt
plt.bar(X_train.columns, dtc.feature_importances_)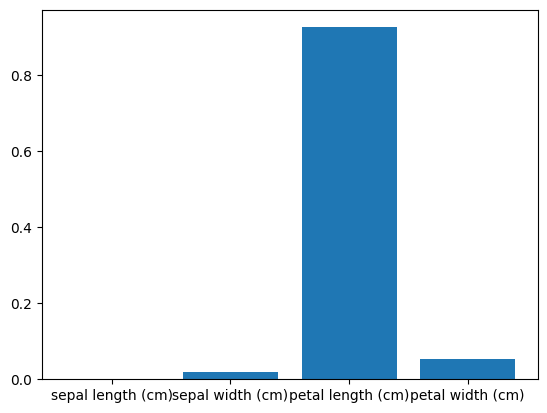

# model plotting
from sklearn.tree import plot_tree
plt.figure(figsize=(10,8))
plot_tree(dtc, feature_names = iris['feature_names'],
		  class_names = iris['target_names'],
          filled = True); #semi를 추가하면 text가 지워짐
plt.show()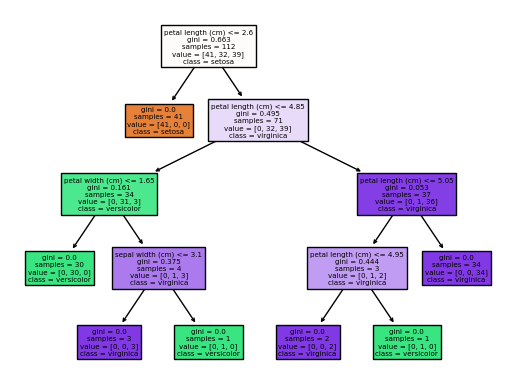

import seaborn as sns
sns.scatterplot(data = X_train,
                x = X_train.columns[2],
                y = X_train.columns[3],
                hue = y_train)
plt.vlines(2.6,0,2.5)
plt.vlines(4.85, 0, 2.5)
plt.hlines(1.65, 2.6, 4.85)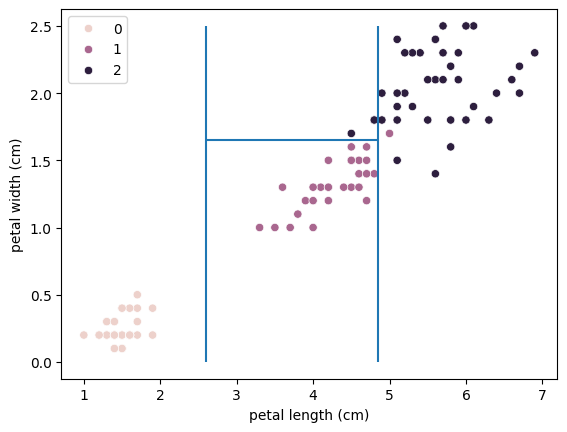

pruning (가지치기)

Decision Tree 모델은 모든 잎 노드의 불순도가 0이 되는 순간까지 모델을 성장시키기 때문에, 순수 노드로만 이뤄진 트리 모델은 훈련 데이터를 100% 정확도로 맞출 수 있다. 때문에 과적합에 취약한데, 이를 방지하기 위해 트리 복잡도를 제어하는 방법이 가지치기 이다.

modeling parameter - max_dept: 트리의 최대 깊이

설정을 할 수는 있는데, 잘 안쓰는 parameter
max_leaf_nodes : 잎 노드의 최대 개수
min_sample_leaf : 잎 노드가 되기 위한 최소 샘플 갯수
min_sample_split : 잎 노드가 분지되기 위한 최소 샘플 갯수

code

dtc = DecitionTreeClassifier(max_depth=3, random_state=42)
plot_tree(dtc, feature_names = iris['feature_names'],
		  class_names = iris['target_names'],
          filled = True); #semi를 추가하면 text가 지워짐

Decision tree regressor

그렇다면 classification말고 prediction은 어떻게 할 수 있을까?

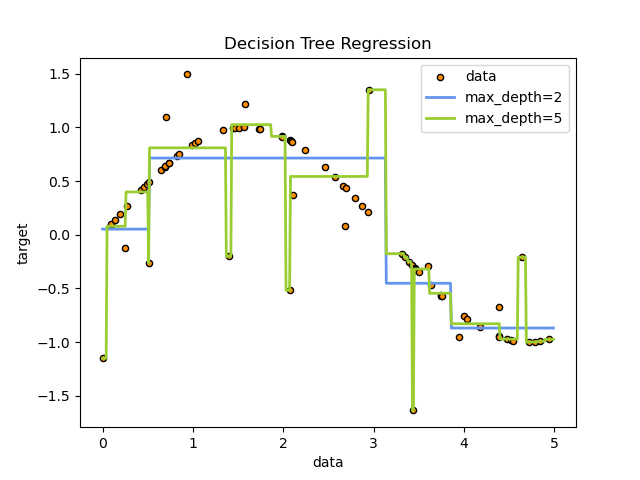
노드에 속한 학습 샘플의 값의 평균을 바탕으로 예측값을 결정함.
Regression 과 동일하게 MSE가 최소화 되도록 모델링을 진행한다

아무래도 데이터가 비선형일 경우 오히려 linear regression이나 poly linear regression보다 더 잘 맞는 경우도 많음.

Random Forest

Random Forest는 Decision Tree모델의 모형 결합(ensemble) 방법론

2-depth까지 들어가기 때문에 해석이 어려워짐

ensemble(앙상블)

복수의 예측모델(기본적으로 100개)을 결함하여 더 나은 성능을 예측한다
단일 모형을 사용할 때 보다 성능 분산이 감소하고, 과적합을 방지한다
앙상블 방법론에는 배깅, 부스팅이 있다

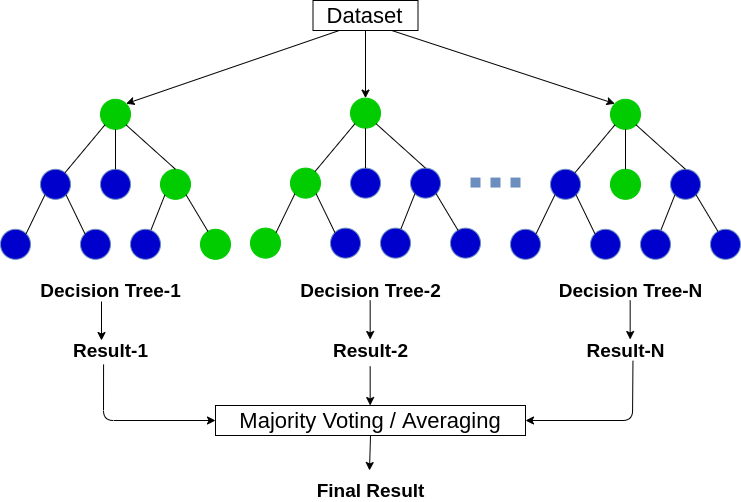
가장 큰 특징은 모델을 병렬구성하고 학습을 한꺼번에 시킴

bagging(배깅)

개별 모델을 병렬로 구성하여 모델을 결합하는 방법론
기존 학습 데이터에서 복원 추출로 여러개의 sub sample 데이터 셋을 만든 후 각 데이터셋을 병렬 구성 모델에 학습시켜 다른 결과를 얻는다
개별 모델의 결과값을 voting 또는 평균법을 사용해 개별 모델 결과를 바탕으로 최종 추정치를 얻는다

Random Forest Bootstrap Aggregating

Random forest는 대표적인 bagging 방법론으로 weak-model로 Decision Tree를 사용한다.
Bagging 사용 시 추가적으로 bootstrap 방법론을 추가하여 모델 학습에 사용한다.
Bootstrap은 복원 추출된 sub-sample 데이터셋 생성 시 랜덤 샘플 및 feature를 선택하여 모델 학습에 사용한다

Code

# model generation
from sklearn.ensemble import RandomForestRegressor
rfr = RandomForestRegressor(random_state=42)
rfr.fit(X_train, y_train)
y_pred = rfr.predict(X_test)

# score
from sklearn.metrics import r2_score, mean_squared_error
print(f'r2_score : {r2_score(y_test, y_pred)}')
print(f'rmse : {mean_squared_error(y_test, y_pred,squared=False)}')

퍼포먼스를 끌어올리고 과적합을 방지하기 위한 모델링 파라미터

n_estimators : 사용할 Tree model 갯수 (병렬 구성할 모델의 개수, default = 100)
max_depth : 트리의 최대 깊이

Parameter Searching

tree base model은 설정 가능한 parameter의 조합에 따라 모델의 예측력 차이가 큰 특징을 가지고 있습니다. 때문에 Parameter Searching을 꼭 진행해야 합니다.

^-^ 주의 - 절대 Test data를 여기에 쓰지 말 것
train - validation - test 로 data_set을 새롭게 만들어서 해야함

Code

# genearte validation data
X_train2, X_val, y_train2, y_val = train_test_split(X_train, y_train, test_size = 0.3, random_state = 42)

# import module
from itertools import product

# make all combination using product function
est = [50, 70, 90, 100, 150, 200, 300, 500]
depth = [3, 5, 7, 9, 11, 13, 15, 17]

best_score = 0
best_param = None

for param in product(est, depth):
	print(f'[{param}] searching')
	model = RandomForestRegressor(n_estimators = param[0],
    							  max_depth = param[1], random_state=42)
	model.fit(X_train2, y_train2)
	pred = model.predict(X_val)
	r2 = r2_score(y_val, pred)
	if best_score < r2:
		best_score = r2
		best_param = param
		print('new score')
print('searching finish')

print(best_param, best_score)
best_model = RandomForestRegressor(n_estimators = best_param[0], max_depth = best_param[1], random_state = 42) #Bootstrap에 대한 랜덤성을 고정시킴
best_model.fit(X_train, y_train)
best_pred = best_model.predict(X_test)
print(r2_score(y_test, best_pred))

Boosting Tree

Bagging과 Boosting의 차이는 학습을 위해 사용하는 개별 모델을 병렬/직렬로 구성함에 있다.
Bagging의 경우 sub sample에 따라 개별 모델을 모두 학습시키고 결과를 투표 혹은 평균을 내어 예측하지만,
Boosting은 개별 모델의 학습을 순차적으로 시키며 이전 개별 모델의 결과 중 오분류 된 데이터 혹은 오차에 가중치 부여

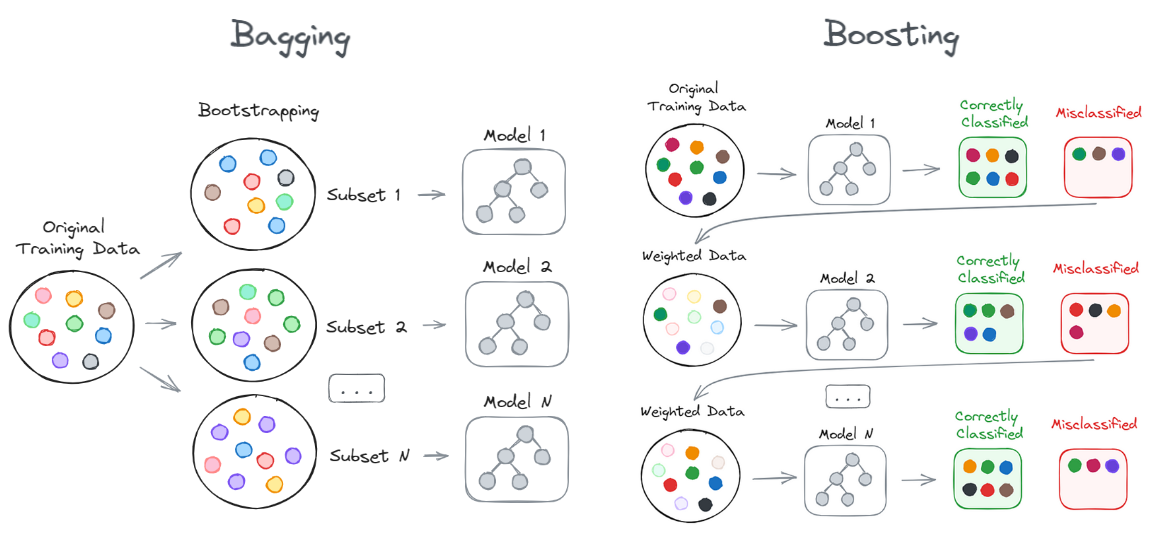
Bagging과 비교했을 때, Bagging은 메모리가 많이 필요하지만 속도가 빠르고
Boosting은 메모리가 적게 필요하지만 속도가 느리다.

초기에는 동일 가중치를 갖지만, 각 과정을 거치며 복원 추출 시 가중치의 분포/이전 round의 오차를 고려

Adaboost, GBM, Xgboost, lightGBM, catboost

Adaptive boosting = Adaboost

각 학습 단계(각 round)에서 오분류된 데이터에 가중치를 부여하고 다음 round에서 가중치가 부여된 데이터를 잘 맞추기 위한 개별모델이 학습된다.
최종 모델은 개별 모델의 결과가 합쳐져서 최종 모델링이 된다.

눈치챌 수 있겠지만 모델이 많이 복잡하고
실제 이로 인한 퍼포먼스가 뛰어난 것도 아니라서
초창기에 인기가 없었음

Gradient boost = GBM

이전 round model의 오차를 학습해서 점진적으로 총 모델링 오차를 줄이는 부스팅 방법

$y = h_0(x) + error_0$
$error_0 = h_1(x) + error_1$
$error_1 = h_2(x) + error_2$
$\vdots$
$y = h_0(x) + h_1(x) + h_2(x) + \cdots + small error$

당연히, 과적합 될 수 있음
하지만 이 해결이 아무래도 어려움

xgboost

gadient boosting에 학습을 위한 비용 함수에 규제화 식이 추가되어 모델이 과적합 되는 것을 방지함.
규제화를 통해 복잡한 모델에 패널티를 부여

$obj^{(t)} = \sum_1^{n} l(y_i, \hat{y}_i^{(t)}) + \sum_{i=1}^t \Omega(f_i)$

$t = round$

참고논문

Code

# install model
!pip install xgboost

# model import
from xbgoost import XGB
# modeling
xgbr = XGBRegressor()
xgbr.fit(X_train, y_train)
xgbr_pred=xgbr.predict(X_test)
print(r2_score(y_test, xgbr_pred))
print(mean_squared_error(y_test, xgbr_pred, squared=False))
# feature_importance print
plt.figure()
plt.bar(X_train.columns,xgbr.feature_importances_)
plt.show()

xbgoost 주요 파라메터

모델 파라메터
verbosity : round 출력결과 0=무음, 1=경고, 2=정보, 3=디버그
n_jobs : 병렬쓰레드 구성, 로컬컴퓨터 코어 x 4 최대값
gpu_id : GPU 연산 처리 디바이스 설정
random_state : 랜덤시드
missing : 결측치 처리 np.nan을 디폴트로 사용

트리 파라메터
max_depth : 트리모델 최대 깊이
max_leaves : 트리모델 최대 잎 노드 갯수, 0=무제한 지정
grow_policy : 트리확장 방법 0=노드와 가장 가까운 노드 분할, 1=손실함수가 최소가 되는 지점에서 분할
gamma : 트리모델의 잎 노드 분할을 만드는 데 필요한 최소 손실 감소.
min_child_weight : 관측치에 대한 최소 가중치 값
subsample : 부트스트랩 샘플 비율
colsample_bytree : 부트스트랩 컬럼 비율
reg_alpha : L1, lasso, 0
reg_lambda : L2, ridge, 1

부스팅 파라메터
n_estimators : 부스팅 트리 갯수, round 횟수와 같은 수
learning_rate : round별 학습률(cost function의 최솟값을 찾을 때, gradient를 찾아가는 보폭이라고 생각할 수 있음)
booster: 부스팅 트리 모델 선택
- gbtree
- gblinear
objective : 목적함수(=비용함수)
- reg : squarederror
- binary : logistic
- multi : softmax
- multi : softprob
eval_metric : 모델평가함수, 목적함수에 따라 지정되어 있음 <-boosting model은 매 round에서 이전 round보다 더 낮은 오차를 가져가야하는데, 그때에 평가하는 값
- rmse: root mean square error
- error: Binary classification error rate (0.5 threshold)
- merror: Multiclass classification error rate
early_stopping_rounds : 학습 손실값 변동 없을 시 학습 종료 라운드 횟수 설정(=오차가 계속 줄어야하는데 몇번 라운드를 진행했는데 오차가 줄어들지 않을 때, 그 라운드 횟수를 설정하는 옵션)
callbacks : 학습 중 설정 값 전달 API

GridSearchCV

모델이 복잡해질수록 설정할 수 있는 여러가지 parameter값들이 생기는데, 이를 각각 테스트 해서 최고의 퍼포먼스를 내는 parameter를 찾아야함.
이 과정을 편하게 진행할 수 있는 방법론이 GridSerchCV

내가 궁금해하는 모든 조합을 일일이 다 해보면 힘듦

Cross Validation 교차 검증

validation data의 위치에 따른 영향성을 최소화하기 위해 validation data를 여러 위치에서 뽑으며 최적의 parameter를 찾는 것

보다 잘 되어있는 설명

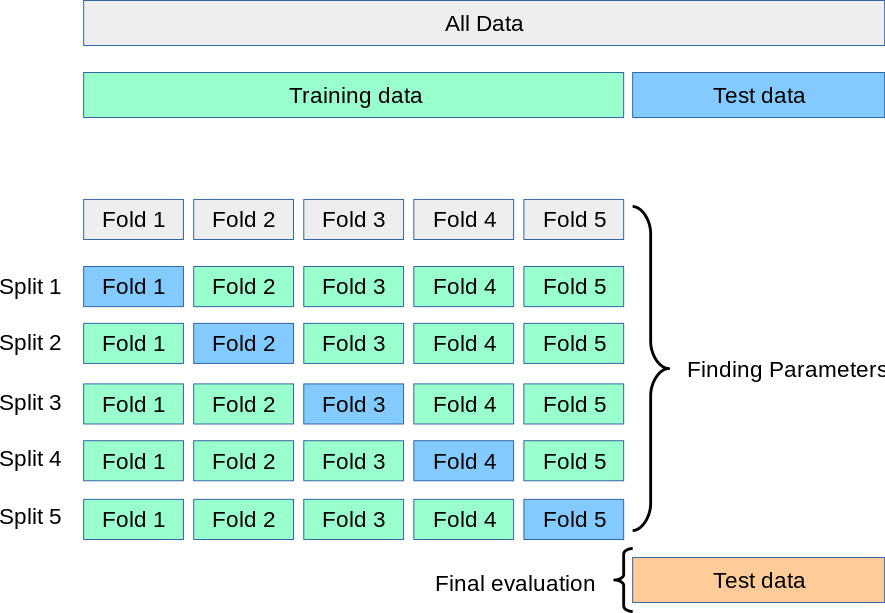
Code

# GridSearchCV for xgboost
## ==========================
## 적용하고 싶은 parameter 고민
## ==========================
## 'max_depth' : [3, 5, 7, 9]
## 'subsample' : [0.7, 0.8, 0.9]
## 'colsample_bytree' : [0.7, 0.8, 0.9]
## 'n_estimators' : [100, 300, 500, 700, 1000]
## 'learning_rate' : [0.03, 0.01, 0.003]
## 'reg_alpha' : [0,1] [1,3,5,7]
## 'reg_lambda : [0,1] [1,3,5,7]

# import grid search
from sklearn.model_selection import GridSearchCV

# import model for search
from xgboost import XGBRegressor
xgbr = XGBRegressor(random_state=42)

# grid search
params = {'max_depth' : [3, 5, 7, 9],
'subsample' : [0.7, 0.8, 0.9],
'colsample_bytree' : [0.7, 0.8, 0.9],
'n_estimators' : [100, 300, 500, 700, 1000],
'learning_rate' : [0.03, 0.01, 0.003]
} # dictionary 형태로 제작

grid = GridSearchCV(estimator = xgbr,
                    param_grid = params,
                    scoring = 'neg_root_mean_squared_error', #scoring 참조
                    verbose=2,
                    cv = 5 # 5-fold cross validation
                    )
                    
grid.fit(X_train, y_train)

# chek best parameter
grid.best_params_

# grid가 이미 best parameter를 적용한 model을 가지고 있음
grid.predict(X_test)

scoring 참조