1. 개요

• 두 양적 자료 간에 통계적으로 직선의 관계(선형의 관계)가 있는지 검정하는 방법
• 선형적으로 증가 혹은 감소하는지를 나타냄
• 두 변수간의 연관된 정도를 나타낼 뿐 인과관계를 설명하는 것이 아님
• 인과관계는 회귀분석을 통해 확인할 수 있음
  

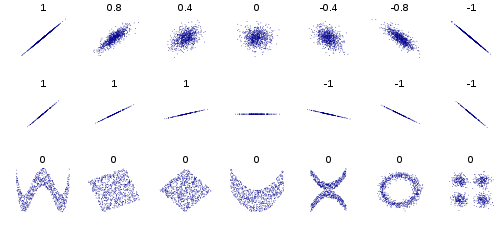
2. 상관계수 행렬도

data.corr(method = 'pearson' or 'spearman' or 'kendall')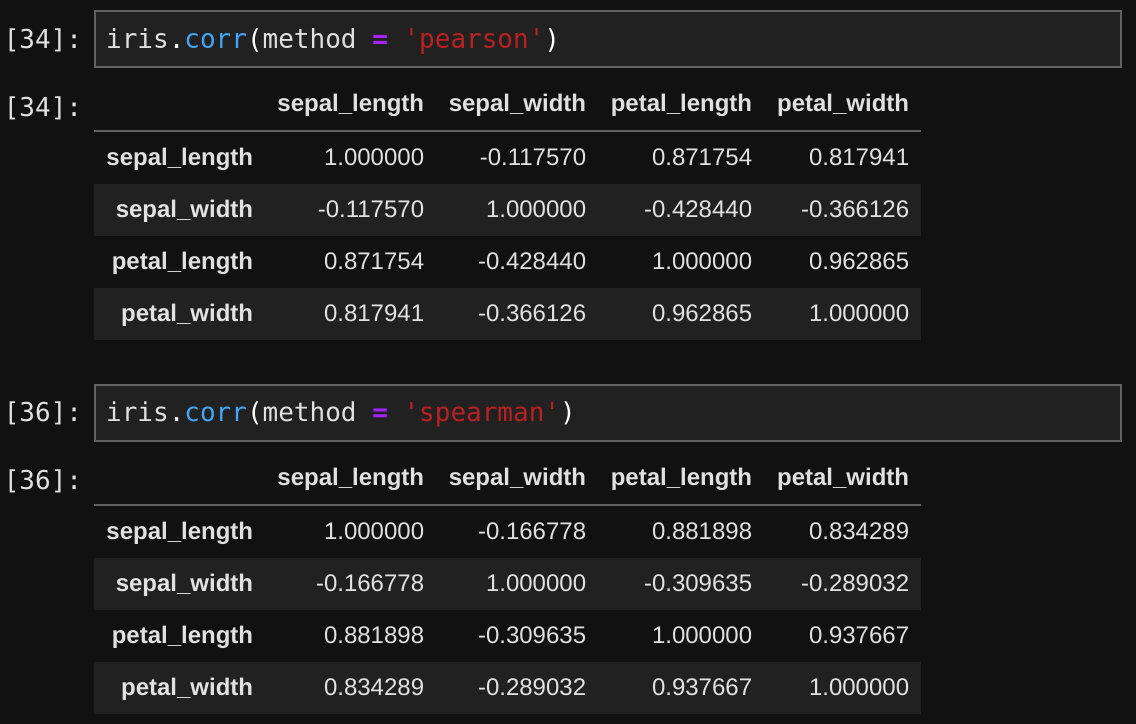

3.산점도

• 두 개의 양적자료에 대한 직선의 관계(선형의 관계)가 있는지를 시각화

  import seaborn as sns
  
  sns.pairplot(x_vars = 'variable1', y_vars = 'variable2', data = )
  plt.show()
  
  # 산점 행렬도 (SPM : Scatter Plot Matrix)
  sns.pairplot(data)
  plt.show()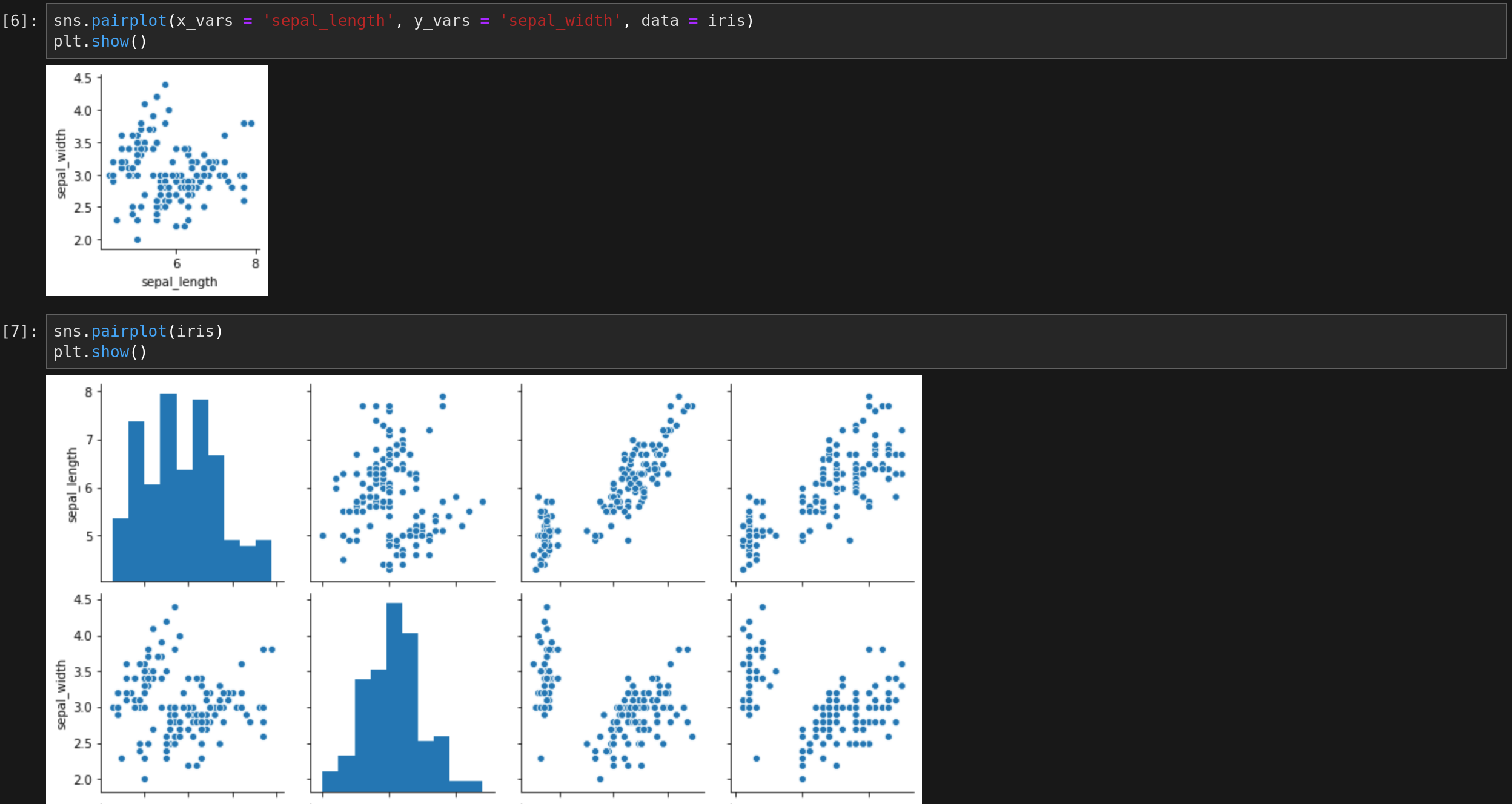

  

4. 상관분석

1) 정규성 검정

• 독립된 집단 두 개이기 때문에 정규성 과정 두 번 실시

2) 가설

• 귀무가설 : 양적자료 1과 양적자료 2 간에는 관련성 (직선의 관계)가 없다.
• 대립가설 : 양적자료 1과 양적자료 2 간에는 관련성 (직선의 관계)가 있다.

(1) 피어슨 상관 계수 (Pearson)

• 피어슨 상관 계수 (r)
• 상관 계수를 구하기 위해 보편적으로 사용되는 방법
• 정규성을 따르는 경우 사용
• 연속형 변수의 상관관계 (신장, 몸무게)

  import scipy.stats as stats
  stats.pearsonr(x = data.variable1, y = data.variable2)

  
• 결론 : 유의확률 0.000이므로 유의수준 0.05에서 양적 자료 간에는 통계적으로 유의한 '양(+)'의 상관관계가 있는 것으로 나타났다.
• 0.872 = 표본의 상관계수 (r)

  참고 : 상관계수 해석의 일반적인 가이드
  |r| = 절대값
  0.0 <= |r| < 0.2 : 상관관계가 없다. = 선형의 관계가 없다.
  0.2 <= |r| < 0.4 : 약한 상관관계가 있다.
  0.4 <= |r| < 0.6 : 보통의 상관관계가 있다.
  0.6 <= |r| < 0.8 : 강한 (높은) 상관관계가 있다.
  0.8 <= |r| <= 1.0 : 매우 강한 (매우 높은) 상관관계가 있다.

(2) 스피어만 상관 계수 (Spearman)

• 정규성 가정이 깨졌을 경우 사용
• 변수값 대신 순위형(순서형 자료)
• 데이터를 작은 것부터 차례로 순위를 매겨 그를 이용하는 방법
• 자료에 이상치가 있거나 표본 크기가 작을 때 유용

  stats.spearmanr(a = data.variable1, b = data.variable2)

  

(3) 켄달 상관 계수 (Kendall)

• 정규성 가정이 깨졌을 경우 사용
• t : tau
• 변수값 대신 순위형(순서형 자료)

stats.kendalltau(x = data.variable1, y = data.variable2)

3) 참고

• 유의성을 도출할 때, 통계적 또는 도메인 유의성이 있는데 도메인이 우선함