모수적 일원배치 분산 분석
일반적으로 3개 이상의 모집단에서 모평균을 비교하는 문제
3개 이상 모집단에서 3개 이상의 평균을 비교하는 경우
범주형 변수 (3가지 이상의 범주값) 수치형 변수 (평균 비교에 사용되는 변수)
평균을 비교하기 전에 세 집단의 분포가 정규분포인지, 집단 간 분산이 동일한지에 따라 그 결과가 다름
3개 이상의 평균 차이가 있다면 사후 분석이라는 다중비교를 할 수 있음
- 일원배치 분산분석은 평균에 차이가 있는지 없는지 판단 가능하며 어느 집단끼리 차이가 있는지에 대해서는 알 수 없다
- 분산분석에서 평균차이가 있다고 판단되면 사후 검정으로 다중비교를 할 수 있다.
여러가지 다중비교 방법 중 Tukey HSD 검정이 있다.
세가지 이상 집단의 평균비교임에도 평균비교라고 하지 않고 분산분석이라고 하는 이유에 대해 살펴봄
k개의 평균 중에 적어도 하나는 차이가 있다라고 하면 귀무가설을 기각
하나도 차이가 없다고 하면 귀무가설 채택
분산의 동일성 검정은 'lawstat'라이브러리 내장 함수 levene.test()로 실시

분산의 동일성 검정은 "Bartlett" 검정(bartlett.test 함수)을 통해서도 확인 가능
Bartlett 검정(bartlett.test 함수)
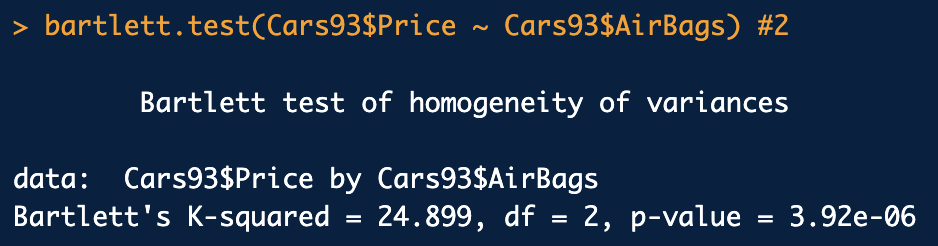
결론: lawstat 검정, Bartlett 검정 모두 집단별 분산이 동일하다 할 수 없다
정규분포이고, 분산이 동일할 때는 avo()함수 또는 oneway.test(Y~X, var.equal=T) 를 사용한다.
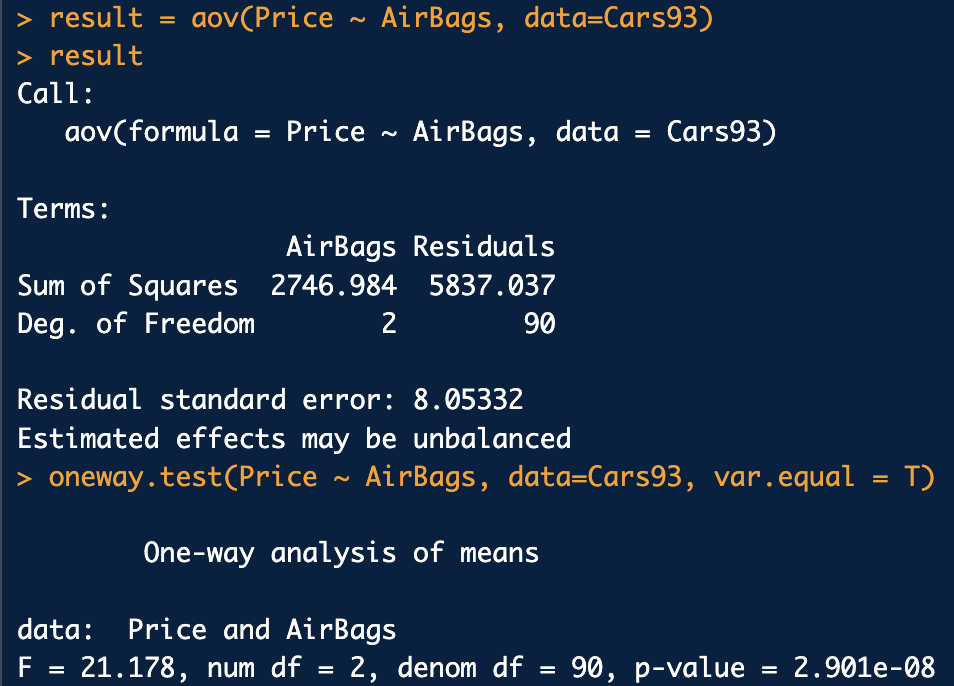
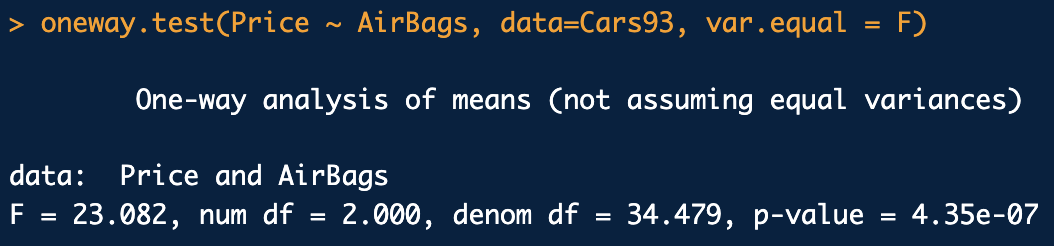
정규분포이고, 분산이 동일하지 않을 때는 oneway.test(Y~X, var.equal=F) 를 사용한다.
Tukey.HDS -> 사후검정법
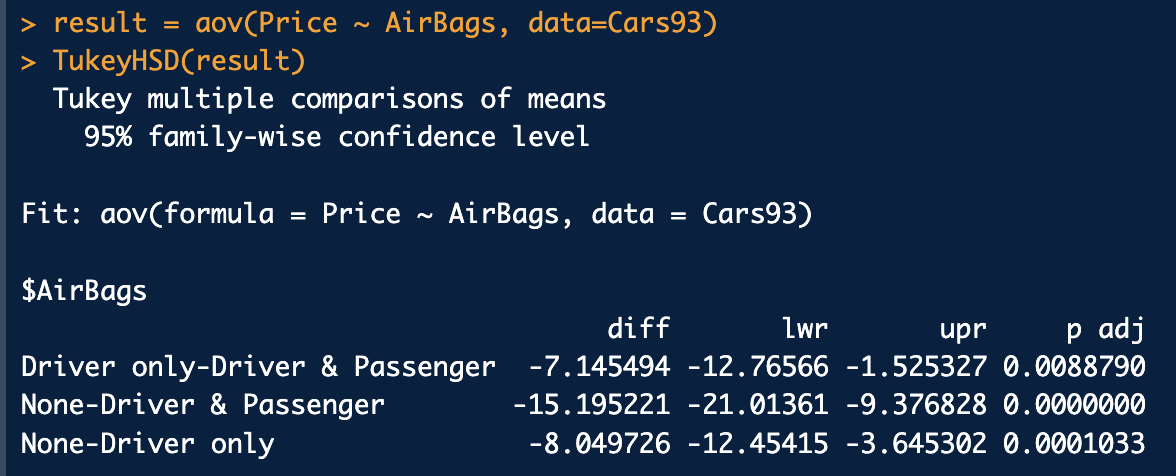
Tukey의 Honest Significant Difference
(Tukey.HDS함수)를 사용하여 다중비교를 실시
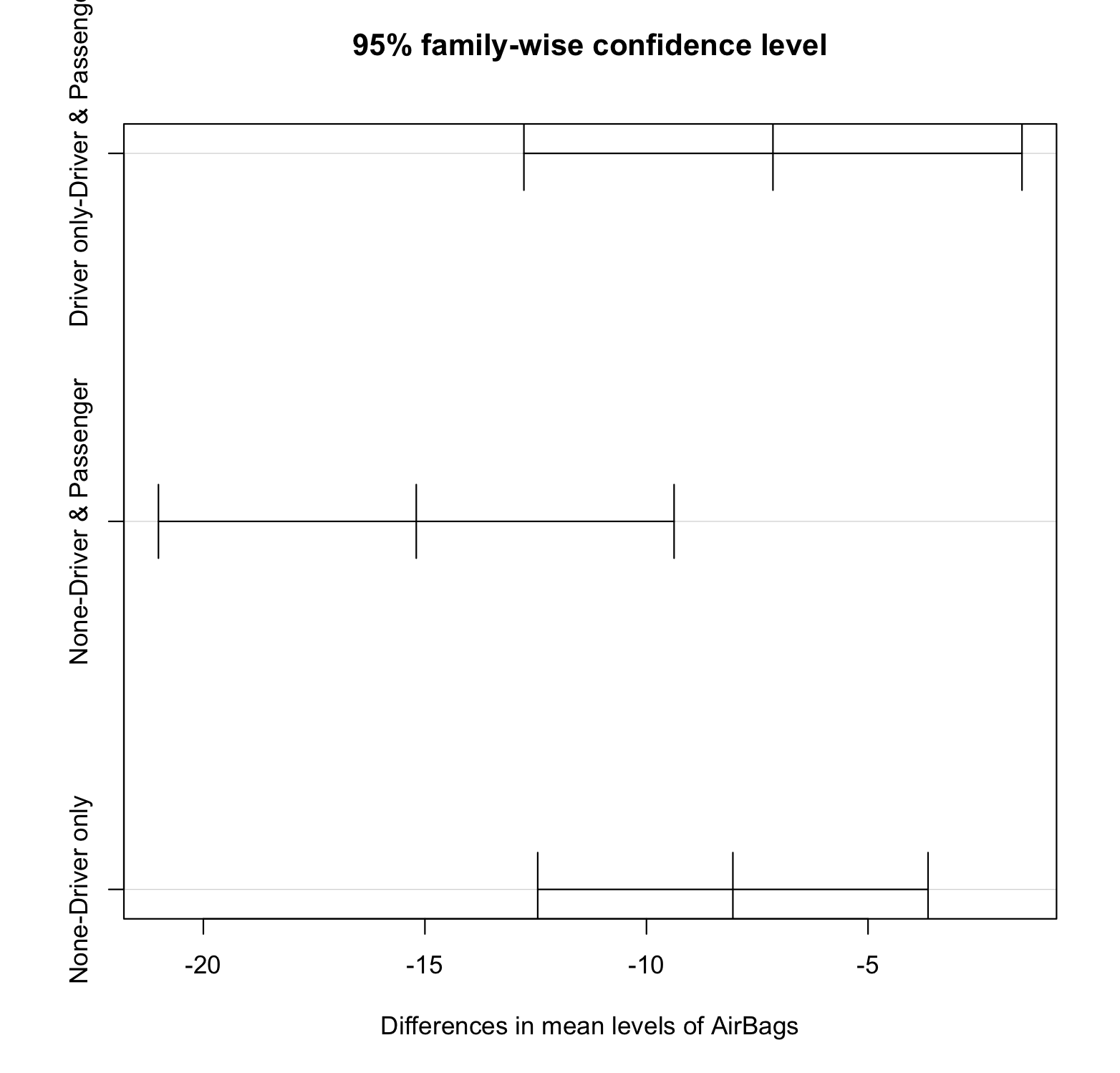
세 그룹 모두 차이가 있다
비모수적 검습
비모수적 검정 (크루스칼 - 왈리스 검정) 세 집단 이상의 평균을 비교할 때 각 집단에서 정규성검정을 만족하지 못하거나 소표본인 경우 실행
-> 순위평균의 차이 여부를 가지고 모집단의 평균 차이 여부를 알아보는 것
분산분석 방법
1. 실험계획
2. 관찰
- 범주형 변수(3가지 이상의 범주값)
- 수치형 변수
정규성을 만족하지 않을 시 Kruskall-Wallis 검정을 실시할 수 있음
densityplot(Price~AirBag, data=Cars93)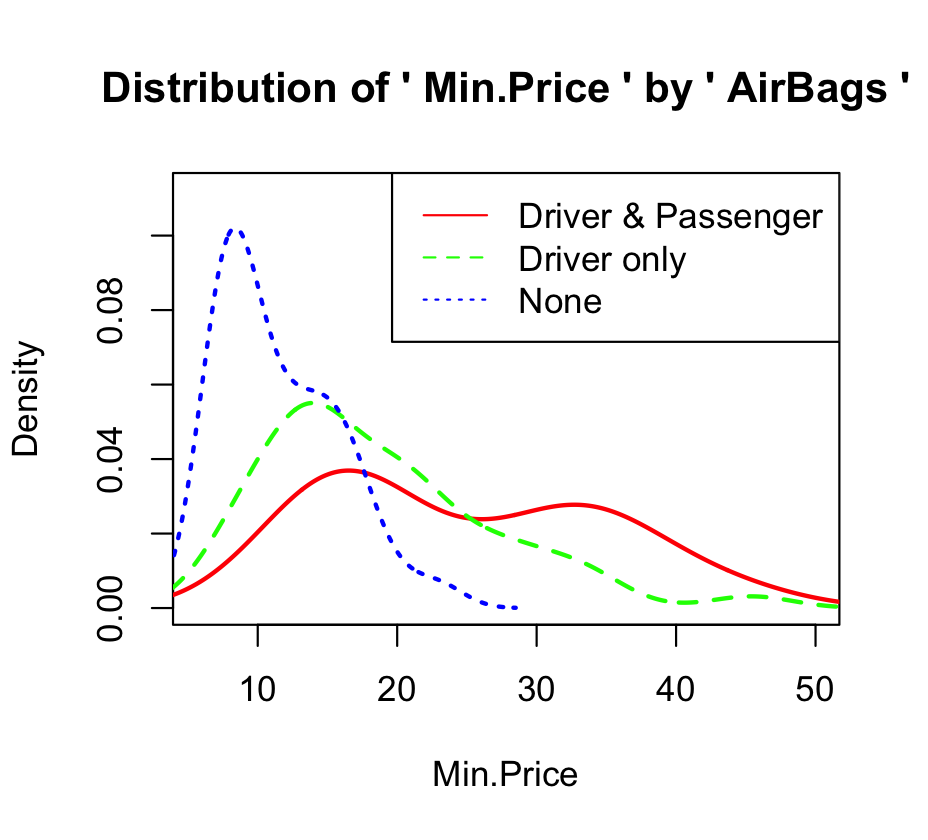
densityplot함수 -> 집단별 분포밀도함수
dunn.test -> 사후 검정
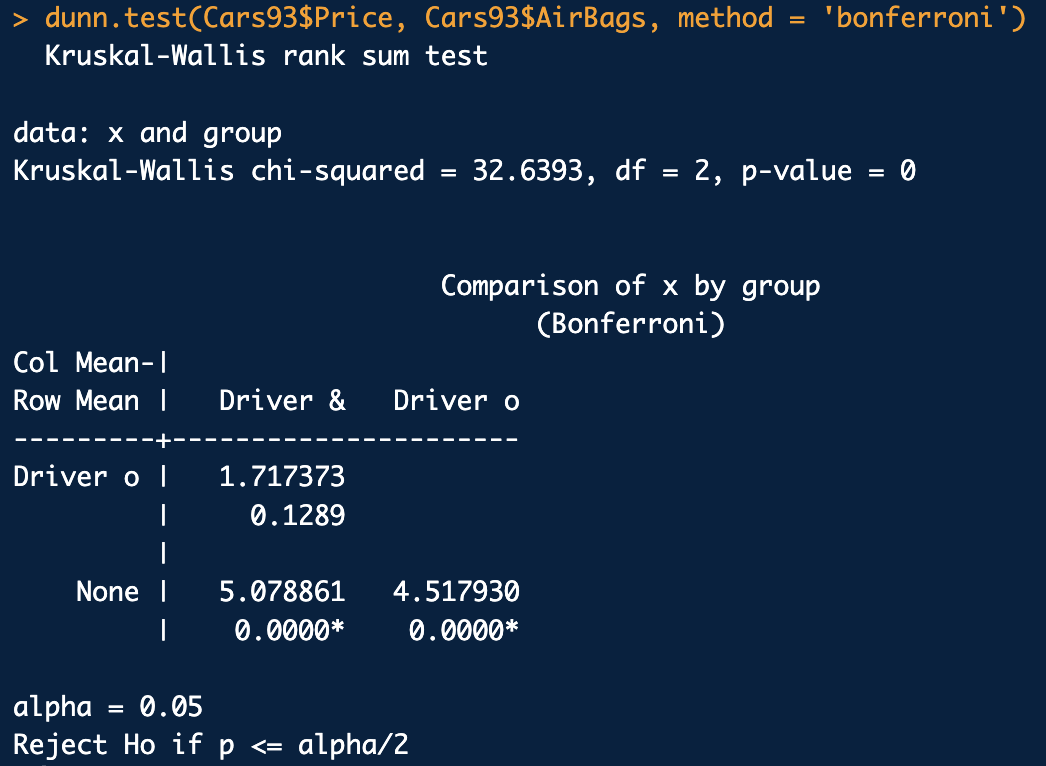
결론
'None' 집단과 'Driver & Passenger' 집단의 가격 평균이 다르다할 수 있음
None' 집단과 'Driver only' 집단의 가격 평균이 다르다할 수 있음
'Driver only' 집단과 'Driver & Passenger' 집단의 가격 평균이 다르다고 할 수 없음
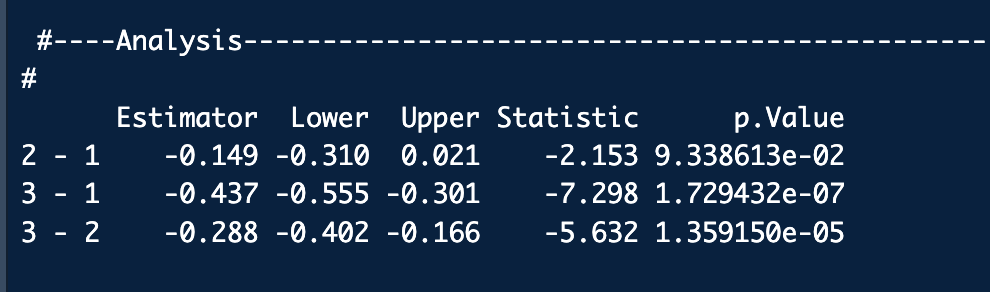
정규분포이고 등분산을 만족하지 않는 경우 mctp함수를 이용하여 사후비교를 할 수 있음
Mctp함수 (ype="Tukey"가 디폴드)
이원배치 분산분석
A, B 요인이 있고 반복이 있을 경우 3가지 가설
A 요인의 각 수준별 종속변수의 평균 차이가 있는가 (A의 주효과)
B 요인의 각 수준별 종속변수의 평균 차이가 있는가 (B의 주효과)
A와 B의 상호작용에 의한 종속변수의 평균 차이가 있는가? (A와 B의 상호작용효과)
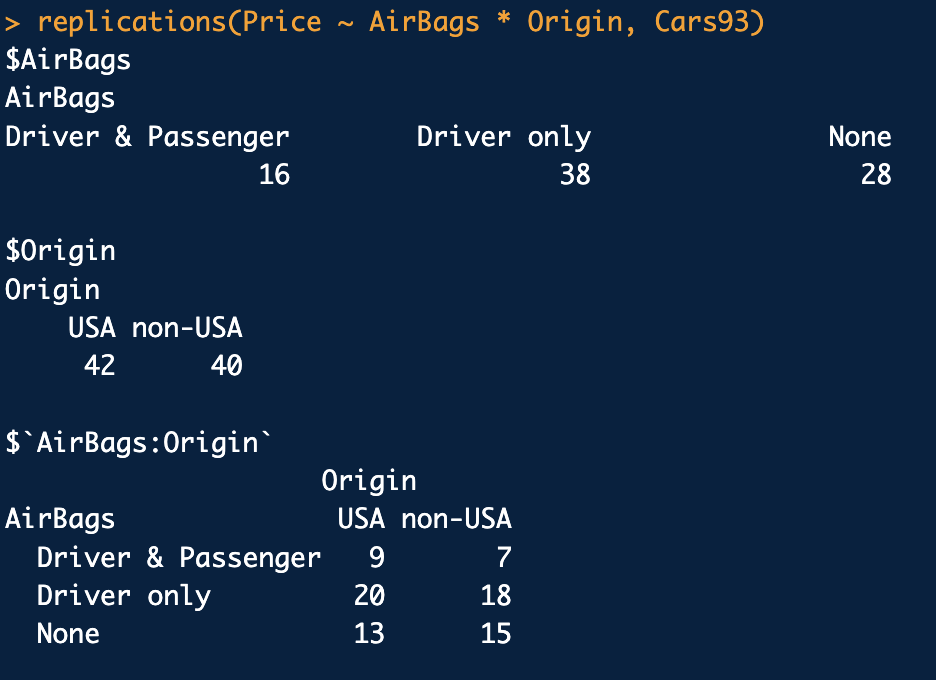
replications()를 통해 균형설계자료인지 확인
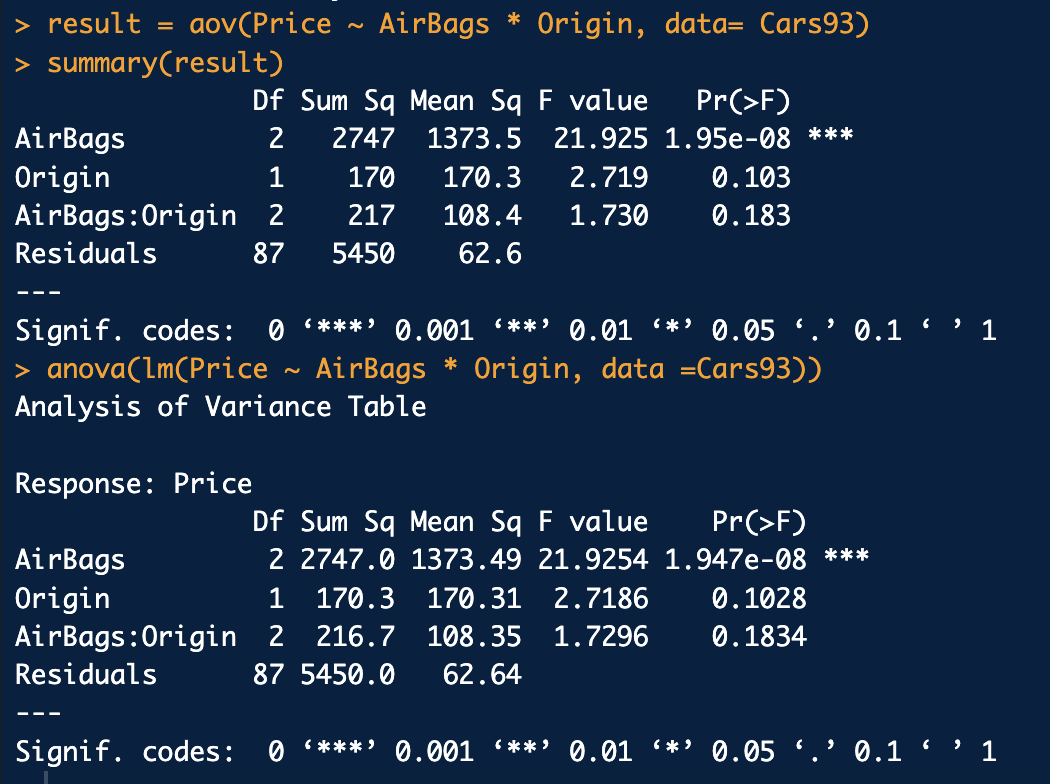
anova()함수를 사용할 경우는 summary()함수 없이 그 결과를 볼 수 있음
불균형자료의 경우는 변동요인의 제곱합을 계산하는 방법이 다릅니다.
type 1 SS : "계층적 접근법" 아무런 통제없이 A의 제곱합이 계산되고, 다음에는 요인 A를 통제한 상태에서 요인 B의 제곱합을 계산하는 방식
type 2 SS : "실험접근법" 한 요인의 주효과는 다른 요인의 주효과만 통제한 상태에서 제곱합을 계산(상호작용효과는 통제 안함)하고, 이원상호작용의 제곱합을 계산할 때는 모든 다른 이원상호작용을 통제한 상태에서 계산
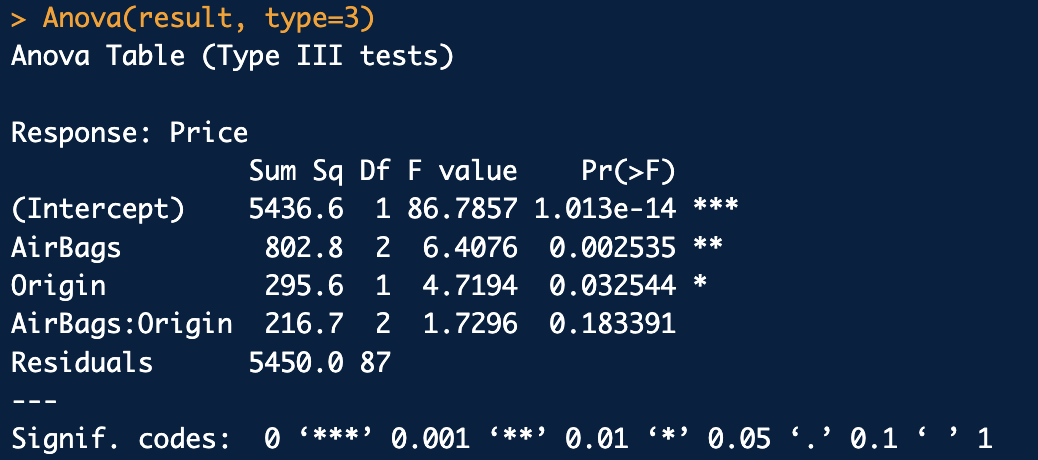
type 3 SS: "유일접근법" 각 요인의 제곱합은 다른 모든 요인들과 상호작용 효과까지 통제 후 계산하고, 보통 불균형 자료에서 type 3 SS를 고려하여 많이 분석함
디폴트 값은 type 2SS
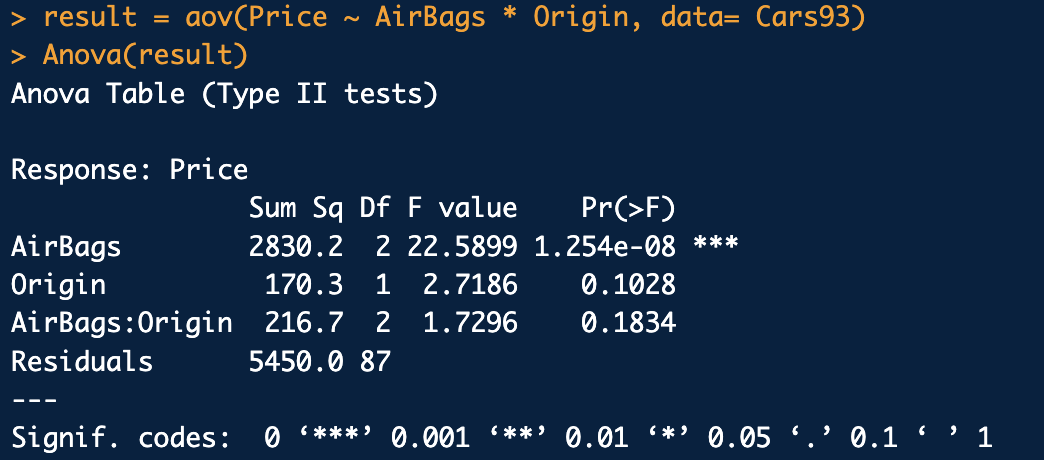
불균형자료에서는 type 3SS를 일반적으로 많이 사용합니다.
friedman.test(종속변수, 요인, 블록) 함수를 사용하여 반복이 없는 블록 자료에 대한 프리드만 검정을 수행
- 출처 통계청 통계교육원