🔥 논문리뷰 - LoRA: Low-Rank Adaptation of Large Language Models

Simple Summary

• LLM을 적은 시간, 비용으로 finetune시키기 위해 등장한 방법
• 기존의 pre-trained weights를 freeze시키고 dense layer의weight를 Low-rank 로 decomposition한 Matrices만을 학습한다

Abstract

• Large-Scale로 학습된 모델 등장, 이를 Full Fine-tuning하면 비용이 엄청나다
• 해당 논문이 제시한 방법은,
  Pretrained model weights를 Freeze하고 학습 가능한 Rank Decomposition Matrices를 각 transformer 구조에 삽입한다.
• Downstream task를 위한 학습 해야할 Parameters를 크게 줄일 수 있다.
  • parmeters수를 10000분의 1, GPU memory를 3분의 1로 줄였다.
  • 거기다 추가적인 Inference Latency가 없다.

---

Introduction

• 특정 task를 수행하기 위해선 Pretrained model의 모든 Weight를 Update해야한다 → 엄청난 비용
• Fine-Tuning의 가장 큰 난관은 새로운 모델이 기존 모델만큼 Parameteres를 가진다는 것
• LoRA는 적은 수의 task-specific한 Parameters만 저장, 학습시키면 된다.
  

• 이전 연구 (Measuring the Intrinsic Dimension of Obejective Landscapes(2018) & Intrinsic Dimensionality Explains the Effectiveness of Language Model Fine-Tuning(2020)) 에서 주장하기로,
  Over-parametrized model은 Low Intrinsic dimension에 존재한다.
• 이를 토대로 본 논문에선 다음과 같이 가정한다
  Model adaptaion 중에 일어나는 Weights의 변화도 Low Instrinsic rank를 가진다
• LoRA는 pretrained weights는 freeze한 채로,
  Dense Layers의 변화의 rank decomposition matrices를 optimize해 Dense Layers를 Train한다.
• 효율적인 저장 및 계산이 가능하다.

LoRA의 주요 장점

• task에 맞는 적절한 A,B를 switch해서 사용할 수 있다
• 대부분 Parameters에 대하여 Gradient를 계산하거나 Optimizer state를 유지할 필요 없이,
  삽입한 매우 작은 Low-Rank Matrices만 Optimize하면 된다.
• Deploy 할 때 Frozen Weight에 merge할 수 있다 → No Infernce Latency

용어 및 규칙 정리
$d_{model}$ : Transformer Layer의 Input, Output 차원 크기
$W_q , W_k, W_v, W_0$ : Self-Attention의 Query, Key, Valye, Output Projection Matrices
$r$ : LoRA의 Rank
$d_{ffn} = 4 * d_{model}$ : MLP Feedforward 차원 크기
※ Optimizer로 Adam 사용

---

Probelm Statement

• LoRA는 Objective에 Agnostic(상관없이 모두 사용 가능) 함. 단 여기선 Language Modeling에 중점.
• $P_{\Phi}(y|x)$ : $\Phi$로 Parameterized된 모델 like GPT
• 해당 모델을 특정 Downstream Task에 적용한다고 가정
  • ex) 요약, MRC, NL2SQL
  • 모두 Context-Target Pairs의 훈련 데이터셋 가짐
    • $Z = \{(x_i, y_i)\}_{i=1,..,N}$
      • $x_i, y_i$는 모두 Token
        • ex) In NL2SQL : x는 자연어 query, y는 대응하는 SQL 명령어.

• Full Finetuning을 하면 모델은 pre-trained Weights인 $\Phi_0$로 초기화 되고 $\Phi_0+\Delta \Phi_0$로 업데이트된다.
  • Objective를 만족하는 Gradient를 Maximize하는 방향
• 가장 큰 문제 : 각 Donwstream task마다 $\Delta$와 같은 크기의 다른 Parameters인 $\Delta \Phi$를 학습해야한다 → 지나친 Cost 발생

• LoRA는 Parameter 증가량인 $\Delta \Phi$를
  훨씬 작은 크기의 Parameters Set인 $\Theta$( $<< \Phi_0$ ) 로 encoded된 $\Delta \Phi(\Theta)$를 학습한다.
• $\Delta \Phi$를 찾는 것이 곧 $\Theta$를 Optimize하는 것
• 기존 Parameters의 0.01% 정도

---

AREN’T EXISTING SOLUTIONS GOOD ENOUGH?

• 이전엔 크게 2가지 방법
  • Adpater Layers를 더한다
  • Input Layer Activations를 Optimize (?)
• Large-Scale and Latency-Sensitive에서 한계가 있다.

Adapter → Inference Latency

• Transformer block에 2개의 Adapter Layers를 더하거나
  Block당 1개에 LayerNorm을 함께 더한다
• Layers를 가지치거나 멀티테스크 세팅을 사용하새 Overall Latency를 줄일 수 있다
• 하지만 Adapter Layers에서 발생하는 추가적인 연산을 피할 수 없다
• Large Neural Netowrks는 Hardware Parallelism에 의존하기에 Adapter Layers를 순차적으로 처리해야하고, 이는 Latency 상승을 야기한다.
  • 특히 모델을 공유해야할 때 악화

• Prefix Tuning은 학습가능한 Parameters에서 성능이 비단조적으로 변화하기 때문에 최적화 어렵다.

---

Our Method

• LoRA는 딥러닝 모델의 모든 Dense Layers에 적용 가능하지만 본 논문에선 오직 Transformer Language Models에 집중한다

LOW-RANK-PARAMETRIZED UPDATE MATRICES

• NN에는 행렬곱을 하는 Full-rank( row == col ) Dense Layers가 많다
• Pre-trained Language Model은 Low Intrinsic Dimension(고유 차원)을 가지고 더 작은 subspace에 random projection을 하더라도 효율적으로 학습할 수 있다
  • 즉, 대부분의 중요한 features를 유지하기 때문에 성능도 유지
• 이에 기반해, Adaptation동안 Weights update 할 때도 Low Intrinsic Rank를 가진다.
• $W_0 + \Delta W = W_0 + BA$
  • $W_0(d*k)$ : Pre-trained Weight Matrix
  • $B=d*r, A=r*k$
  • $r<<\min(d,k)$
  • $W_0$는 Freeze, A,B는 학습가능 parameters.
• Forward Pass : $h= W_0x+\Delta W_x = W_0x + BAx$
  • $W_0, \Delta W$는 같은 input(x)에 곱해지고 coordinate-wise하게 합해진다.
  • 초기화 시: $A$ = Random Gaussaian, $B$ = 0 ➡ $\Delta W = BA = 0$
  • $\Delta Wx$는 $\frac{alpha}{rank}$ 로 scale

• 다른 task로 switch할 때 $BA$를 빼주고 새로운 $B^`A^`$를 더해주면 되는데, 이는 거의 메모리 소요가 없다 → No Additional Inference Latency

Applying LoRA to Transformer

• LoRA는 학습가능한 Parameters 줄이기 위해 사용
• Transformer에는 Self-Attention Module 4개, MLP module 2개
• 이 때 오직 Attention Weight에만 적용하고 MLP는 Freeze → Simplicity와 parameter-efficiency를 위해
  • 다른 Layer에 적용하는 것은 추후 연구에

Benefits

• Memory와 저장공간 사용량 감소
  • VRAM 1.2TB → 350GB
  • Checkpoint 350GB → 35MB
• Deploy될 때 훨씬 더 적은 Cost로 task를 바꿀 수 있다

Limitations

• 추가적인 Inference Latency를 줄이기 위해 A,B를 W에 Absorb하면, Single Forward Pass에서 A와 B가 다른 task에 대한 input을 batch 하는 것이 쉽지 않다

---

Empirical Experiments

• 존재하는 Weight Matrices와 대응하는 Rank Decomposition Matrices를 더한다
• 본 논문에서는 Simplicity를 위해 $W_q , W_v$에만 LoRA를 적용했다
• $\Theta=$ 2 X LoRA를 적용한 Matrices의 수 X Layer 차원 크기 X Rank

다른 방법과 비교 결과
GPT-2 medium (M) and large (L) with different adaptation methods on the E2E NLG Challenge

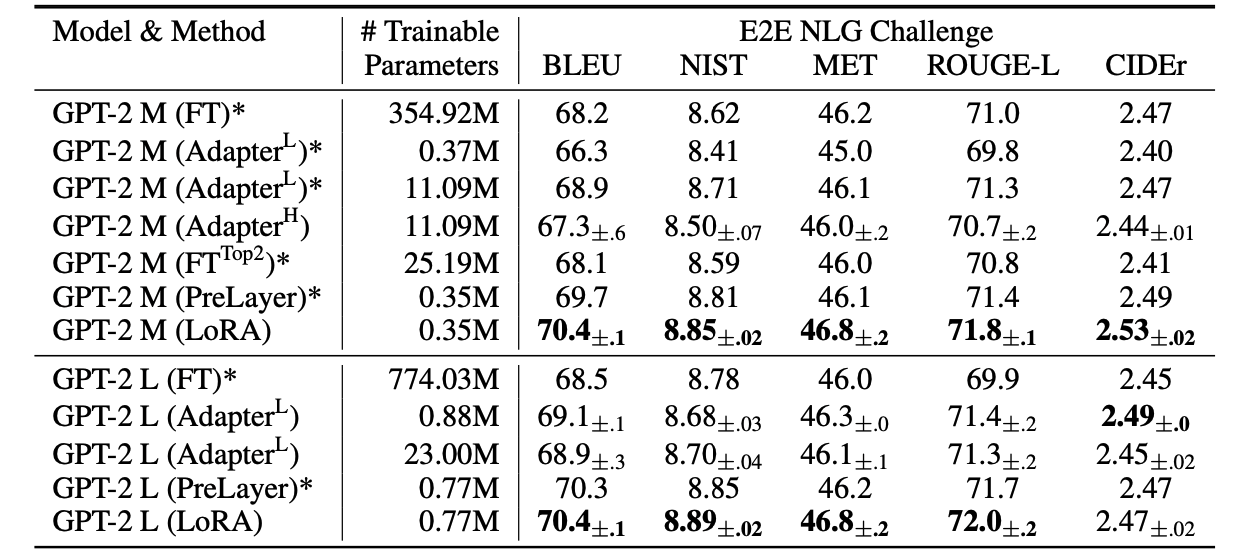
Performance of different adaptation methods on GPT-3 175B

---

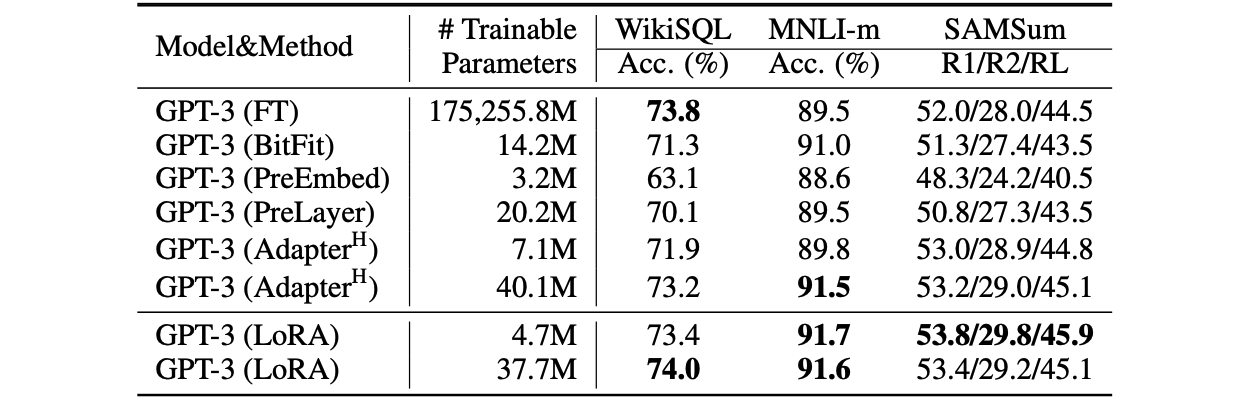
Related Works

Transformer Language Model
Prompt Engineering and Fine-Tuning
Parameter-Efficient Adaptation
Low-Rank Structures in Deep Learning

• 많은 머신러닝 문제가 특정한 Intrinsic Low-Rank structure를 가진다.
• 특히 거대 모델을 사용한 딥러닝 Task의 경우 will enjoy low-rank properties after training(?)
• 하지만 본 논문 이전까지 low-rank update를 고려하지 않았다

---

UNDERSTANDING THE LOW-RANK UPDATES

• Low-Rank Structure로 Hardware로 인한 장벽을 없애
  • 다양한 실험을 병렬적으로 진행 가능
  • 기존 weight에 대한 Update weight 더 잘 해석 가능

해당 질문에 답변할 수 있다

• Which subset of weight matrices in a pre-trained Transformer should we adapt to maximize downstream performance?
  • 본 논문에서는 오직 Self-Attention Module만 고려했다
  • $W_q, W_v$에 adapting하는게 Best
  • 한 종류 Matrices에 큰 Rank 적용하기보다 여러 Matrices에 적용하는 것이 좋다
• Is the “optimal” adaptation matrix ∆W really rank- deficient? If so, what is a good rank to use in practice?
  • r이 매우 작아도 (1 or 2) 충분히 좋은 성능가진다 & r을 증가시켜도Supspace가 더 의미있진 않다
    ➡ $\Delta W$가 매우 작은 Intrinsic Rank 가진다
• What is the connection between ∆W and W ? Does ∆W highly correlate with W ? How large is ∆W comparing to W?
  • $\Delta W$는 $W$와 강한 상관관계
  • ∆W only amplifies directions that are not emphasized in W
    ➡ 즉 low-rank adaptation matrix는 보통 Pre-trained 모델에서 강조되지 않지만 Downstream task에는 필요한 features를 Amplify

---

Conclusion and Future Works

• 거대한 언어 모델을 Fine-tuning하는 비용은 매우 비싸
• LoRA를 사용해서 높은 model quality를 유지하면서 Inference Latency와 Sequnce Length(?)를 줄인다
• 서비스로 사용할 때 대부분의 모델 parameters를 공유하며 빠르게 task-switching이 가능하다
• Transformer Language Models뿐만 아니라 Dense Layers를 가진 모든 Neural Networks에 적용가능하다

• 다른 adapation 방법과 결합
• $\Delta W$ 뿐만 아니라 $W$도 rank-deficient할 수 있다

---

Questions After Review

• Q. LoRA는 어디서 Inspired?

  • A. over-parametrized models in fact reside on a low intrinsic dimension 라는 개념을 이전 논문에서 차용했고 이를 실제 FT에 적용하는 아이디어는 본 논문이 처음

• Q. LoRA의 핵심 개념은?

  • A. change in weights during model adaptation also has a low “intrinsic rank" 즉 가중치의 변화 또한 Low Intrinsic Rank를 가진다고 가정한다

• Q. 왜 Transformer의 Attention Module에만 적용했을까?

  • A. 그 부분이 가장 연산적으로 어렵고 비싸기 때문. 또한 이것이 key component of SOTA models인 경우가 많기 때문이다

• Q. Stable Diffusion FT하는데 어떻게 사용?

  • A. Denoising Unet의 Cross Attention Moduel(query ≠ key = value)에 적용했다

---

※ 출처 및 참고
LoRA Paper : Low-Rank Adaptation of Large Language Models(https://arxiv.org/pdf/2106.09685.pdf)
LoRA Github : https://github.com/microsoft/LoRA
Hugging face/peft Github : https://github.com/huggingface/peft