Regression

회귀라고도 합니당

Regression toward the mean
- Sir Francis Galton

어떤 데이터들이 크거나 작더라도, 전체적으로 봤을 때 전체 평균으로 되돌아 간다는 통계적 원리를 설명한 것이라고 합니당. 이걸 줄여서 Regression(회귀)라고 합니당.

Linear Regression

데이터를 가장 잘 대변하는 직선의 방정식 찾기

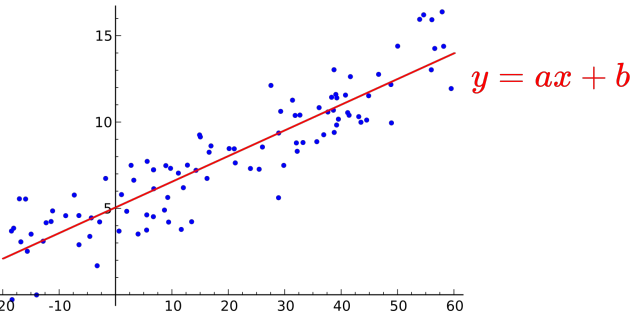
파란색 점을 데이터라고 하면, 이 데이터 전체를 잘 대변하는 직선을 찾는 것을 선형 회귀Linear Regression이라고 합니당.

직선의 기본 형식은 y = ax + b로 a는 기울기, b는 y 절편입니당. 선형 회귀Linear Regression는 이 a와 b를 구해 적절한 직선을 찾는 것이라고 보면 됩니당.

Hypothesis

가설 함수라고도 불려요

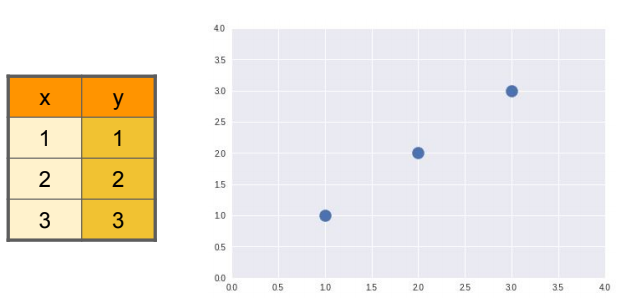
다행히도 전 수학을 열심히 해서(ㅎ) 그림을 보면 어떻게 선을 그어야 저 점데이터을 전체적으로 잘 대변할 수 있을지 보입니당

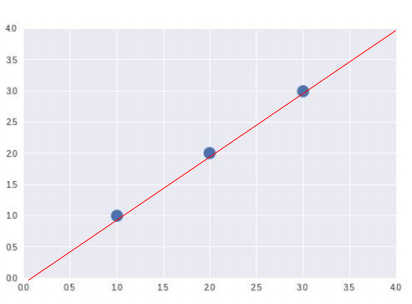
바로 이 모든 데이터를 대변하는 적절한 함수(여기선 직선의 방정식이겠죠?)를 가설함수Hypothesis Function라고 합니당

하지만 우리 컴퓨터는 점데이터만 보고 바로 저렇게 선을 못 그어요 ㅠ
따라서 우리는 학습을 통해 컴퓨터가 선을 정할 수 있게 해줘야 합니당.
즉, 직선 함수의 a와 b를 스스로 구할 수 있게 해야 합니당

이제부터 a를 W라 칭하게 됩니당. 가중치라는 의미가 있어용.

Cost Function

우선 얼마나 정확, 아니 오차가 존재하는지 알아야 합니다

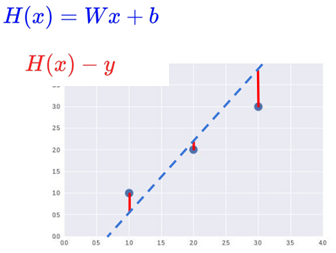
파란색 점선 가설 함수Hypothesis Function가 있습니당. 빨간색 선은 점데이터와 가설 함수Hypothesis Function의 차를 나타냅니당.

가설 함수Hypothesis Function 점데이터에 잘 대변할수록 각 값들은 0으로 수렴하게 됩니당. 그렇게 되면 그만큼 오차가 줄어든다는 의미가 됩니당.

이 오차를 평균을 내면 그만큼 전체적으로 얼마나 오차가 적은지 알 수 있게 됩니당.

이처럼 가장 적은 오차의 가설함수를 도출하기 위해 사용되는 함수를 비용 함수Cost Function(또는 손실 함수Loss Function)이라고 합니당

제곱을 해줍니다

근데 여기서 그대로 끝내기엔 오차의 평균을 내기가 어렵습니당. 왜냐하면 오차 값이 음수일수도 있거든용.

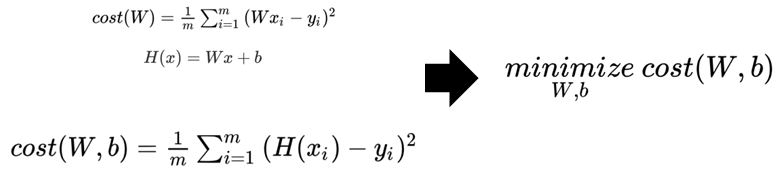
그래서 이 빨간색 선의 값을 제곱해줘서 그런 문제를 해결하면서 동시에 작은 수치에 오차 값에도 민감하게 반응하도록 만들어주었습니당. 이러한 비용 함수Cost Function를 평균 제곱 오차Mean Squared Error(MSE)라고 합니당.

그리고 이 수치를 최소화Minimize하는 W와 b를 찾는 것이 머신러닝의 목표가 됩니당