추천화 시스템 07. 유사도 개념 이해하기

추천 시스템에선 기존 유저나 아이템의 평점을 기반으로 추천을 수행한다고 했습니당.

무분별하게 성향이 다른 녀석들도 같이 사용한다면 좋은 결과를 예측할 수 없다고 해서 유사도를 통해 이를 보완한다고 했어용.

그럼 유사도의 종류와 이에 대해서 알아보기로 하시졉

Cosine Similarity

$cos(\theta) = cos(X, Y) = \frac{X \cdot Y}{\lvert X \rvert\lvert Y \rvert} = \frac{sum_{i=1}^{N} X_{i}Y_{i}}{\sqrt{sum_{i=1}^{N} X_{i}^{2}}\sqrt{sum_{i=1}^{N} Y_{i}^{2}}}$

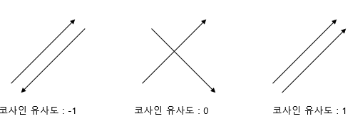
• 주어진 두 벡터 X, Y에 대한 각도를 이용하여 구할 수 있는 유사도
• 직관적으로 두 벡터가 가리키는 방향이 얼마나 유사한지를 의미
  • 두 벡터 방향이 비슷할 수록 1에 가까움
  • 방향이 정반대일 수록 -1에 가까움
• 두 벡터의 차원은 같아야 한다는 전제에 진행해용
• 가장 많이 쓰이는 유사도입니당

Mean Squared Difference Similarity

• MSD & MSC 유사도(아이템)

$msd(u,v) = \frac{1}{\lvert I_{uv} \rvert} \cdot \sum_{i \in I_{uv}}(r_{ui} - r_{vi})^{2}, \text{msdSim}(u,v) = \frac{1}{msd(u,v) + 1}$

• MSD & MSC 유사도(유저)

$msd(i,j) = \frac{1}{\lvert U_{ij} \rvert} \cdot \sum_{u \in U_{ij}}(r_{ui} - r_{uj})^{2}, \text{msdSim}(u,v) = \frac{1}{msd(i,j) +1}$

• 추천시스템에서 가장 많이 사용되는 유사도
• 각 기준(유저, 아이템)에 대한 점수의 차이를 계산하며, 유사도는 유클리드 거리에 반비례합니다.
• 분모에 1을 더하는 이유는 분모가 0이 되는 것을 방지Smoothing

해당 유사도는 Surprise 라이브러리에서 제공된다고 합니당!

Jaccard Similarity

$J(A,B) = \frac{\lvert A \cap B \rvert}{\lvert A \cup B \rvert} = \frac{\lvert A \cap B \rvert}{\lvert A \rvert + \lvert B \rvert - \lvert A \cap B \rvert}$

• 주어진 집합 A, B에 대한 집합의 개념을 사용한 유사도
• Cosine, Pearson과 달리 길이가 달라도 이론적으로 유사도를 구할 수 있어용
• 두 집합이 얼마나 유사한 아이템을 공유하고 있는가를 나타냅니당
  • 두 집합이 가진 아이템이 모두 같으면 1
  • 두 집합이 겹치는 아이템이 하나도 없으면 0
• 실제로 잘 안쓰인다고 합니당

Pearson Similarity

$pearsonSim(X,Y) = \frac{sum_{i=1}^{N} (X_{i} - \bar{X})(Y_{i} - \bar{Y})}{\sqrt{sum_{i=1}^{N} (X_{i} - \bar{X})^{2}}\sqrt{sum_{i=1}^{N} (Y_{i} - \bar{Y})^{2}}}$

• 주어진 벡터 X, Y에 대해서 각 벡터를 표본평균으로 정규화한 뒤, cosine 유사도를 구한 값
• (X와 Y가 함께 변하는 정도) / (X와 Y가 따로 변하는 정도)
• 1에 가까우면 양의 상관관계, 0에 가까우면 서로 독립, -1에 가까울 수록 음의 상관관계를 나타냅니다.