NLP Tutorial (2) - 손실 함수와 최적화

이로운·2025년 6월 5일

AI Foundation model NLP Robotics machine learning

NLP_tutorial

목록 보기

2/8

손실 함수(Loss function)

손실 함수라는 키워드는 굳이 AI나 컴퓨터 비전 관련 전공자가 아니어도, 로보틱스 관련 공부를 해봤다면 들어봤거나 특정 함수의 결과물을 산출하기 위해 설계 해봤을 것이다. 손실 함수, 목적 함수(Objective Function), 비용 함수(Cost function)이란 키워드로 불리기도 하는데, 엄연히 구분하자면 목적 함수는 함수값의 결과를 최대값 혹은 최소값으로 최적화하는 함수를 말하며, 비용 함수는 전체 데이터에 대해 오차를 계산하는 함수를 말한다. 굳이 따지자면, 목적 함수가 최상위의 키워드이고 그 아래에 비용 함수, 그리고 그 아래에 손실 함수가 있다고 생각하면 된다.

손실 함수의 명확한 뜻은 실제값과 예측값 사이의 차이가 발생했을 때, 오차가 얼마인지 계산하는 함수를 말한다. 직관적으로 말하자면 "얼마나 다른가"를 나타내는 함수이다. 이를 수식으로 표현하자면,

\mathcal{L}(y, \hat{y})

보통 이런 형태로 작성하며, 여기서 $y$ 는 실제값, $\hat{y}$ 는 예측값을 말한다. 신경망은 실제값과 예측값을 통해 계산된 오차값을 최소화하는 방향으로 학습이 진행된다. 가장 대표적으로, 회귀(Regression) 문제에서 자주 쓰이는 Mean squared error (평균 제곱 오차)의 경우

\mathcal{L}_{MSE} = \frac{1}{n} \sum^{n}_{i=1}{(\hat{y}_i - y_i)^2}

이렇게 표현된다. 만약, 특정 최적화 문제에서 위 함수를 손실 함수로 쓴다면, 오차의 방향은 제곱이 되어 희석되니 방향이 아닌 크기만을 고려하여 최적화를 해나가기 위해 사용될 것이며 절대값을 취하지 않는 이유는 제곱을 적용하면 오차가 큰 값을 더 크게 작용시킬 수 있게 할 수 있기에 오차의 간극을 빠르게 줄여나갈 수 있다.

또 하나 자주 언급되는 함수로는 교차 엔트로피 함수가 있다. 앞서 소개된 평균 제곱 오차는 연속형 변수에 사용되는 손실 함수이지만, 이산형 변수에는 교차 엔트로피 함수가 더 적합하다. 따라서, Classification 문제에서 종종 채택된다. 수식은 아래와 같다.

CE(y, \hat{y}) = -\sum_j{y_i \log{\hat{y}_j}}

예를 들어, 고양이와 강아지를 분류하는 문제에서 입력된 이미지는 고양이라고 가정하자. 그리고 모델이 산출한 확률은 고양이에 대해 0.6, 강아지에 0.4라고 하고 실제 확률은 고양이 1, 강아지 0이다. 이때 수식을 통해 계산하면, $-\log{0.6}$ 값으로 0.51이라는 결과값이 산출된다.

최적화(Optimization)

최적화란 키워드도 비단 학습 분야 뿐만 아니라 많은 곳에서 사용되는 키워드이다. 여기서는 목적 함수의 결과값을 최적화하는 변수를 찾는 알고리즘을 의미한다. 손실 함수에서 인공 신경망은 오차값을 최소화하여 학습 데이터에 대한 가설의 정확도를 높이는 방향으로 학습이 진행되는 것을 알아보았다. 그렇다면 최적화 과정에서, 빠르게 실제값과 가까운 예측값으로 도달하기 위해 어떤 전략을 펼쳐야할까? 간단하게, 미분의 개념을 생각해보자.

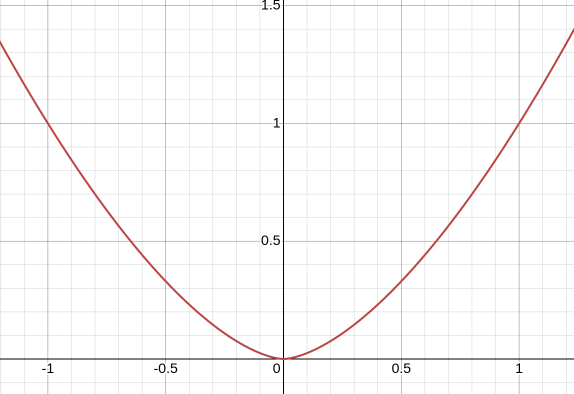
예로, 이러한 가중치-오차 그래프가 있다고 가정하자. 결국, 학습의 목표는 오차가 0이 되는 가중치를 찾는게 목표이고, 그 가중치는 사전에 몰랐다고 할 때, 우리는 특정값을 시작으로 기울기가 0이 되는 시점까지 가중치를 옮겨가며 도달했을 때가 곧 최적의 가중치라고 보면 될 것이다. 그리고, 현재 시작점에서 양의 방향으로 이동해야 하는지, 음의 방향으로 이동해야 하는지, 얼마나 이동해야 하는지를 결정하기 위해, 그 유명한 경사 하강법(Gradient descent) 알고리즘을 사용한다.

W_0 = \mathrm{Initial value}

W_{i+1} = W_i - \alpha\nabla f(W_i)

위 수식은 경사 하강법이 적용되는 수식으로, 초기값에 대해 다음 가중치를 찾는데 여기서 기울기 $\nabla f()$ 가 고려되며 기울기가 0인 방향으로 학습이 진행된다. 이때, 학습률 $\alpha$ 가 가중치 결과를 조정하는데 기여한다. 아래에서 갱신 방법의 수식을 살펴보자. 우선 가설과 손실 함수는 아래와 같이 정의되었다고 하자.

\hat{Y}_i = W_i \times x + b_i

MSE(W,b) = \frac{1}{n}\sum^n_{i=1} (Y_i - \hat{Y}_i)^2

가중치를 갱신을 위해 $W$ 에 대해 편미분을 진행하면, 아래와 같은 일반형 식을 도출할 수 있다.

W_{i+1} = W_i - \alpha \times E[(\hat{Y}_i - Y_i) \times x]

결국 학습률 $\alpha$ 는 다음 가중치를 향한 변화량을 결정하는 키이다. 만약 적절하지 못한 학습률을 설정하면 너무 많은 반복이 필요하거나 최적의 해를 찾지 못하는 문제를 발생시킬 수 있다. 위 그래프는 단순 Parabolic한 형태기에 큰 문제가 없을 수 있지만, 아래 가중치-오차 그래프를 예시로 다시 살펴보자.

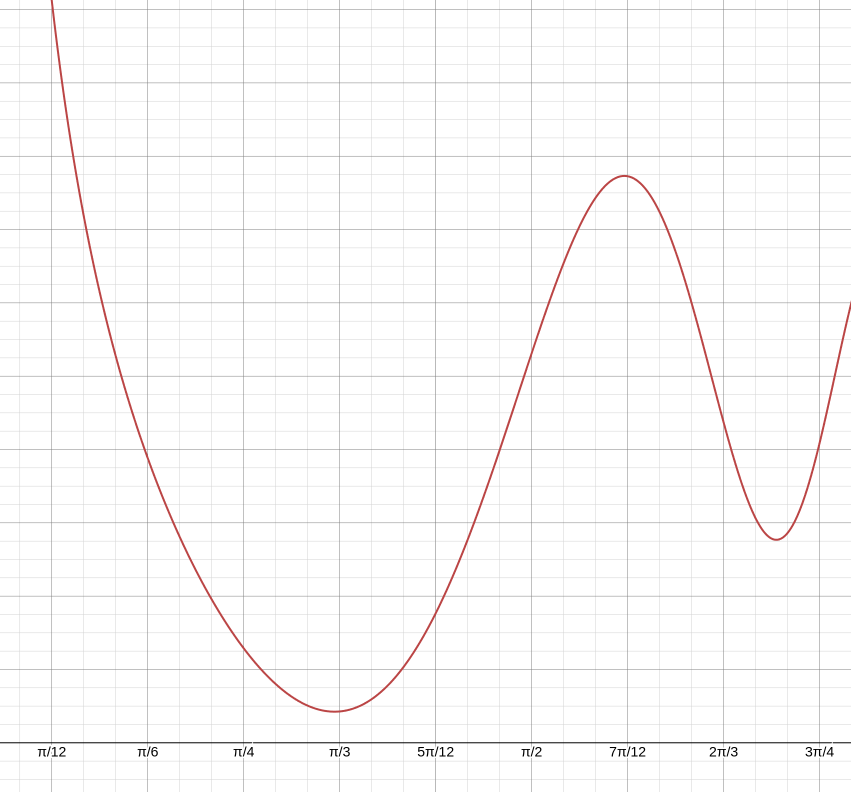
위 그래프는 두 개의 기울기가 0이 되는 지점을 가진다. 하지만, 분명, 더 최적인 점은 존재한다. 이때, 최소값이 아닌 다른 극소값으로 최적화되는 것을 'Local Minima'에 빠진다고 표현을 하기도 하며, 학습률을 너무 낮게 잡으면 이렇게 지역적 최소값을 넘어가지 못하고 빠질 수 있다.

학습에 사용하는 데이터의 형태나 가설, 손실 함수에 따라 적합한 최적화 알고리즘을 선택하는 능력이 요구된다. 경사 하강법이 가장 대표적인 방법이긴 하나, 모멘텀(Momentum), Adaptive Gradient, Adam (Adaptive Moment Estimation) 등의 기법이 있다.

Pytorch 실습

신경망 패키지를 활용하여 간단한 선형 회귀 함수 모델을 도출해보자.

import torch
from torch import optim

x = torch.FloatTensor([[1], [2], [3], [4], [5], [6], [7], [8], [9], [10], [11], [12], [13], [14], [15]])
y = torch.FloatTensor([[0.94], [1.98], [3.02], [4.06], [5.10], [6.14], [7.18], [8.22], [9.26], [10.30], [11.34], [12.38], [13.42], [14.46], [15.50]])

우선 이러한 임의의 데이터셋을 기반으로 진행하자.

weight = torch.zeros(1, requires_grad=True)
bias = torch.zeros(1, requires_grad=True)
learning_rate = 0.01

torch.zeros 메서드로 0을 갖는 텐서를 생성하고, 크기는 1로 설정하며 requires_grad 매개변수를 설정하는데, requires_grad는 모든 텐서에 대한 연산을 추적하며 역전파 메서드를 호출해 기울기를 계산하고 저장한다 (쉽게 말해, 자동 미분 기능의 사용 여부다.).

optimizer = optim.SGD([weight, bias], lr=learning_rate)

이후 최적화 방식을 선언한다. 여기선 확률론적 경사 하강법 (Stocastic Gradient Descent) 방식을 채택하는데, SGD는 일반적인 경사 하강법만 달리 일부 데이터만 계산하여 빠르게 최적화 값을 찾는 방식이다.

for epoch in range(10000):
  hypothesis = x * weight + bias
  cost = torch.mean((hypothesis - y) ** 2)
  
  optimizer.zero_grad()
  cost.backward()
  optimizer.step()
  
if (epoch + 1) % 1000 == 0:
    print(f'Epoch {epoch + 1:04d}/{10000}, Cost: {cost.item():.6f}, Weight: {weight.item():.6f}, Bias: {bias.item():.6f}')

이후 에폭(Epoch)과 가설 그리고 손실함수를 설정한다. 에폭은 신경망에서 순전파와 역전파 과정 등 모델 연산을 전체 데이터세트가 1회 통과하는 것을 말하며, 여러 에폭을 반복해 모델을 학습시킨다, 순전파는 입력 데이터를 기반으로 신경망을 따라 입력층부터 출력층까지 차례대로 연산을 거친 후 추론하는 결과를 말하며, 역전파는 오차가 최소화되도록 가중치를 수정하는 것을 말한다. 에폭값 또한 적절히 설정할 필요가 있다. 에폭이 너무 큰 경우, 과대적합(Overfitting)이 발생할 수 있으며 너무 작으면 과소적합(Underfitting)이 발생한다.

그리고 optimizer.zero_grad() 메서드는 optimizer 변수에 포함시킨 매개변수들의 기울기를 0으로 초기화하고, cost.backward()는 역전파 수행 메서드이다. 그리고 optimizer.step()은 가중치와 편향을 최적화 함수에 반영하는 메서드이다. 이제 결과를 확인하자.

Epoch 1000/10000, Cost: 0.000001, Weight: 1.039782, Bias: -0.097754
Epoch 2000/10000, Cost: 0.000000, Weight: 1.039998, Bias: -0.099975
Epoch 3000/10000, Cost: 0.000000, Weight: 1.040000, Bias: -0.099998
Epoch 4000/10000, Cost: 0.000000, Weight: 1.040000, Bias: -0.099998
Epoch 5000/10000, Cost: 0.000000, Weight: 1.040000, Bias: -0.099998
Epoch 6000/10000, Cost: 0.000000, Weight: 1.040000, Bias: -0.099998
Epoch 7000/10000, Cost: 0.000000, Weight: 1.040000, Bias: -0.099998
Epoch 8000/10000, Cost: 0.000000, Weight: 1.040000, Bias: -0.099998
Epoch 9000/10000, Cost: 0.000000, Weight: 1.040000, Bias: -0.099998
Epoch 10000/10000, Cost: 0.000000, Weight: 1.040000, Bias: -0.099998

출력 결과를 통해, 특정 값으로 각 변수들이 수렴하는 것을 확인할 수 있다.

이번엔 신경망 패키지를 활용한 실습을 해보자.

import torch
from torch import optim
from torch import nn

x = torch.FloatTensor([[1], [2], [3], [4], [5], [6], [7], [8], [9], [10], [11], [12], [13], [14], [15]])
y = torch.FloatTensor([[0.94], [1.98], [3.02], [4.06], [5.10], [6.14], [7.18], [8.22], [9.26], [10.30], [11.34], [12.38], [13.42], [14.46], [15.50]])

model = nn.Linear(1,1)
criterion = nn.MSELoss()
optimizer = optim.SGD(model.parameters(), lr=0.001)

for epoch in range(10000):
  output = model(x)
  cost = criterion(output, y)
  
  optimizer.zero_grad()
  cost.backward()
  optimizer.step()
  
  if (epoch + 1) % 1000 == 0:
    print(f'Epoch [{epoch + 1}/10000], Cost: {cost.item():.6f}, Model : {list(model.parameters())}')

여기선 모델을 선형 변환 클래스를 이용하여 구현하였고, 손실 함수론 평균 제곱 오차를 선택한다.
결과를 확인하고 위와 비교해보자.

Epoch [1000/10000], Cost: 0.044520, Model : [Parameter containing:
tensor([[1.0831]], requires_grad=True), Parameter containing:
tensor([-0.5438], requires_grad=True)]
Epoch [2000/10000], Cost: 0.018191, Model : [Parameter containing:
tensor([[1.0675]], requires_grad=True), Parameter containing:
tensor([-0.3837], requires_grad=True)]
Epoch [3000/10000], Cost: 0.007433, Model : [Parameter containing:
tensor([[1.0576]], requires_grad=True), Parameter containing:
tensor([-0.2813], requires_grad=True)]
Epoch [4000/10000], Cost: 0.003037, Model : [Parameter containing:
tensor([[1.0512]], requires_grad=True), Parameter containing:
tensor([-0.2159], requires_grad=True)]
Epoch [5000/10000], Cost: 0.001241, Model : [Parameter containing:
tensor([[1.0472]], requires_grad=True), Parameter containing:
tensor([-0.1741], requires_grad=True)]
Epoch [6000/10000], Cost: 0.000507, Model : [Parameter containing:
tensor([[1.0446]], requires_grad=True), Parameter containing:
tensor([-0.1474], requires_grad=True)]
Epoch [7000/10000], Cost: 0.000207, Model : [Parameter containing:
tensor([[1.0429]], requires_grad=True), Parameter containing:
tensor([-0.1303], requires_grad=True)]
Epoch [8000/10000], Cost: 0.000085, Model : [Parameter containing:
tensor([[1.0419]], requires_grad=True), Parameter containing:
tensor([-0.1194], requires_grad=True)]
Epoch [9000/10000], Cost: 0.000035, Model : [Parameter containing:
tensor([[1.0412]], requires_grad=True), Parameter containing:
tensor([-0.1124], requires_grad=True)]
Epoch [10000/10000], Cost: 0.000014, Model : [Parameter containing:
tensor([[1.0408]], requires_grad=True), Parameter containing:
tensor([-0.1079], requires_grad=True)]

결론적으로 위와 유사한 weight와 bias를 얻었지만 다른 것을 확인할 수 있다.

이로운

Robotics Engineer / https://www.linkedin.com/in/roun-lee-5503382b6/

이전 포스트

NLP Tutorial (1) - Pytorch 기초

다음 포스트