NLP Tutorial (3) - 활성화 함수

이로운·2025년 6월 6일

AI Deep Learning NLP activation function machine learning

NLP_tutorial

목록 보기

3/8

활성화 함수(Activation function)

손실 함수만큼 학습에서 중요하게 결정해야 할 요소는 활성화 함수이다. 활성화 함수는 신경망의 각 노드(뉴런)이 입력 신호를 받은 뒤 "어떤 값을 출력할지" 결정하는 은닉층 활성화 함수를 말한다. 활성화 함수는 가중치와 편향으로 이루어진 노드를 선형에서 비선형으로 갱신하는 역할을 한다.

왜 비선형 함수가 필요한가?에 대해 먼저 말하자면, 우리가 특정 데이테와 결과 사이의 관계, 즉 '모델'을 잘 표현하기 위해선 선형 변환만으론 아무리 심층 구조를 갖더라도 결국 선형 모델이다. 예를 들어, 특정 모델을 위한 여러 변수 중에선, 어떤 변수는 더 많은 가중치를 가져야 할 것이고, 어떤 변수는 비교적 덜 활성화 되어야할 필요성이 있다. 결론적으로, 활성화 함수는 데이터 값을 정해진 수식에 따라 변환하여 입력값에 대한 출력값을 비선형으로 변환 및 비선형성을 추가하여 신경망이 더 복잡한 패턴을 학습할 수 있도록 하는 역할을 한다.

참고로 비선형 활성화 함수는 보편 근사 정리(https://ko.wikipedia.org/wiki/%EB%B3%B4%ED%8E%B8_%EA%B7%BC%EC%82%AC_%EC%A0%95%EB%A6%AC)에 따르면, 단 한 층의 은닉층과 활성화 함수의 조합만으로도 적절한 근사를 이뤄낼 수 있게 된다.

이진 분류

이진 분류는 규칙에 따라 입력된 값을 두 그룹으로 분류하는 작업을 말한다. 이진 결과를 분류하기에 논리 회귀(Logistic Regression) 또는 논리 분류(Logistic Classification)이라고도 부른다. 이진 분류기에 결과를 0~1 범위로 예측해야하며, 이때 시그모이드(Sigmoid) 함수와 같은 활성화 함수를 주로 사용한다.

Sigmoid(x) = \frac{1}{1+e^{-x}}

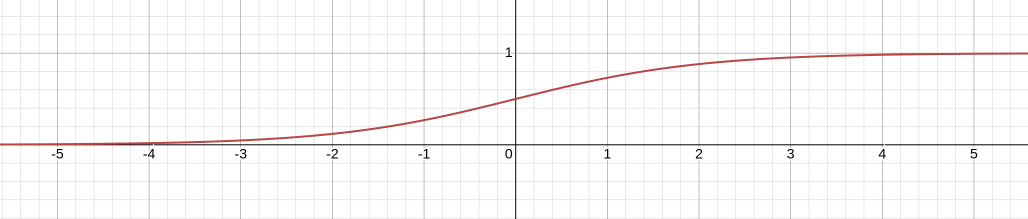
위는 시그모이드 함수의 식과 그래프로, x의 계수에 따라 경사를 결정한다. 학습 중 은닉층에서 도출한 결과가 다시 시그모이드 함수를 통해 나온 출력값이 0.5보다 낮으면 거짓으로 분류하며 크면 참으로 분류한다.

이진 분류 실습

우선 이 임의 데이터셋으로 이번 실습을 진행한다.
혹시 만약 마땅한 데이터셋이 없으시다면, 아래 코드로 만들면 OK

import numpy as np
import pandas as pd

def generate_binary_classification_csv(
    file_path: str,
    n_samples_per_class: int = 500,
    mean_diff: float = 2.0,
    random_seed: int = 42
):
    """
    이 함수는 이진 분류용 CSV 파일을 생성합니다.
    - 클래스 0: 평균 (0, 0), 공분산 행렬 I
    - 클래스 1: 평균 (mean_diff, mean_diff), 공분산 행렬 I
    - 최종 데이터는 두 클래스를 합쳐서 무작위로 섞은 후 저장합니다.

    Parameters:
        file_path (str): 생성할 CSV 파일 경로
        n_samples_per_class (int): 클래스당 샘플 개수 (기본값: 500)
        mean_diff (float): 클래스 1의 평균이 (mean_diff, mean_diff)인 점
        random_seed (int): 난수 시드 (기본값: 42)
    """
    np.random.seed(random_seed)

    # 클래스 0 데이터 (평균: (0,0))
    class0_features = np.random.randn(n_samples_per_class, 2) + np.array([0, 0])
    class0_labels = np.zeros(n_samples_per_class, dtype=int)

    # 클래스 1 데이터 (평균: (mean_diff, mean_diff))
    class1_features = np.random.randn(n_samples_per_class, 2) + np.array([mean_diff, mean_diff])
    class1_labels = np.ones(n_samples_per_class, dtype=int)

    # 두 클래스를 병합
    features = np.vstack((class0_features, class1_features))
    labels = np.concatenate((class0_labels, class1_labels))

    # 인덱스를 섞어서 데이터 순서 섞기
    indices = np.arange(features.shape[0])
    np.random.shuffle(indices)
    features = features[indices]
    labels = labels[indices]

    # Pandas DataFrame으로 변환
    df = pd.DataFrame(features, columns=['feature1', 'feature2'])
    df['label'] = labels

    # CSV 파일로 저장
    df.to_csv(file_path, index=False)
    print(f"CSV 파일이 생성되었습니다: {file_path}")

if __name__ == "__main__":
    # 예시 실행: 현재 디렉토리에 'binary_data.csv' 파일 생성
    generate_binary_classification_csv("binary_data.csv")

위 코드로 얻어진 샘플 데이터로 이진 분류기를 만들어보자.

import torch
import pandas as pd
from torch import nn, optim
from torch.utils.data import DataLoader, Dataset, random_split

class CustomDataset(Dataset):
  def __init__(self, csv_file):
    df = pd.read_csv(csv_file)
    self.x1 = df.iloc[:, 0].values
    self.x2 = df.iloc[:, 1].values
    self.y = df.iloc[:, 2].values
    self.length = len(df)
    
  def __getitem__(self, idx):
    x = torch.tensor([self.x1[idx], self.x2[idx]], dtype=torch.float32)
    y = torch.tensor(self.y[idx], dtype=torch.float32)
    return x, y
  
  def __len__(self):
    return self.length
  
class CustomModel(nn.Module):
  def __init__(self):
    super().__init__()
    self.layer = nn.Sequential(
      nn.Linear(2, 1), # 입력 차원 2(데이터 특징 개수), 출력 차원 1
      nn.Sigmoid()
    )
  
  def forward(self, x):
    x = self.layer(x)
    return x
  
dataset = CustomDataset("../binary_data.csv")
dataset_size = len(dataset)

train_size = int(0.8 * dataset_size)
validation_size = int(dataset_size * 0.1)
test_size = dataset_size - train_size - validation_size

train_dataset, validation_dataset, test_dataset = random_split(dataset, [train_size, validation_size, test_size])

train_dataloader = DataLoader(train_dataset, batch_size=32, shuffle=True, drop_last=True)
validation_dataloader = DataLoader(validation_dataset, batch_size=4, shuffle=True, drop_last=True)
test_dataloader = DataLoader(test_dataset, batch_size=4, shuffle=True, drop_last=True)

device = "cuda" if torch.cuda.is_available() else "cpu"
model = CustomModel().to(device)
criterion = nn.BCELoss().to(device)
optimizer = optim.Adam(model.parameters(), lr=0.001)

for epoch in range(10000):
  cost = 0.0
  
  for x, y in train_dataloader:
    x, y = x.to(device), y.to(device)
    
    optimizer.zero_grad()
    output = model(x)
    loss = criterion(output, y.unsqueeze(1))  # y를 (batch_size, 1) 형태로 변환
    loss.backward()
    optimizer.step()
    
    cost += loss
    
  cost = cost / len(train_dataloader)
  
  if (epoch + 1) % 1000 == 0:
    print(f'Epoch [{epoch + 1}/10000], Cost: {cost.item():.6f}, Model : {list(model.parameters())}')
    
with torch.no_grad():
  model.eval()
  for x, y in validation_dataloader:
    x, y = x.to(device), y.to(device)
    
    print("inputs:", x)           # 입력(features) 출력
    print("labels:", y)           # 정답(label) 출력
    output = model(x)
    loss = criterion(output, y.unsqueeze(1))  # y를 (batch_size, 1) 형태로 변환
    print(f'Validation Loss: {loss.item():.6f}')
    
    print("outputs:", output)     # 모델 출력
    print(output >= torch.FloatTensor([0.5]).to(device))
    print("---------------------------")

위는 간단히 구현된 이진 분류기 전체 코드이고, 주요 라인별로 살펴보자.

class CustomModel(nn.Module):
  def __init__(self):
    super().__init__()
    self.layer = nn.Sequential(
      nn.Linear(2, 1), # 입력 차원 2(데이터 특징 개수), 출력 차원 1
      nn.Sigmoid()
    )

Module 클래스를 상속받아 사용자 정의 모델을 정의하고, Sequential을 활용하여 레이어 층을 구성한다. 아래엔 순차적으로 실행될 모듈을 적어주는데, 여기선 입력 데이터 차원이 2, 그리고 출력 차원은 1로 정의하며, 시그모이드 함수를 적용한다.

criterion = nn.BCELoss().to(device)

모델 구성 이후엔 이진 교차 엔트로피 오차 함수를 적용한다. 이진 교차 엔트로피 클래스는 비용 함수로 criterion 인스턴스에서 순전파를 통해 나온 출력값과 실제값을 비교하여 오차를 계산한다.

inputs: tensor([[ 2.4600,  1.3223],
        [ 2.1685,  3.3176],
        [ 1.2816,  2.8949],
        [ 0.2450, -0.5069]], device='cuda:0')
labels: tensor([1., 1., 1., 0.], device='cuda:0')
Validation Loss: 0.019278
outputs: tensor([[0.9646],
        [0.9979],
        [0.9750],
        [0.0135]], device='cuda:0')
tensor([[ True],
        [ True],
        [ True],
        [False]], device='cuda:0')

코드를 작동하면 이런 식으로 출력이 나올 것이다. 출력에서 확인할 수 있듯, 입력된 데이터에 대해 예측값이 산출되고, 그 예측값에 대해 다시 정해진 임계값 0.5를 기준으로 분류가 되는 것을 확인할 수 있다.

다양한 활성화 함수

앞서 소개했듯, 좋은 학습을 위해선 네트워크에 비선형성을 추가해야하고, 이를 위해 다양한 활성화 함수가 사용된다. 정말 많은 함수가 있지만, (작성자 기준) 많이 사용되면서도 수식적으로 생소한 함수들을 몇 개 소개해보고자 한다.

(1) 하이퍼볼릭 탄젠트 함수(tanh)

Tanh(x) = \frac{e^x - e^{-x}}{e^x + e^{-x}}

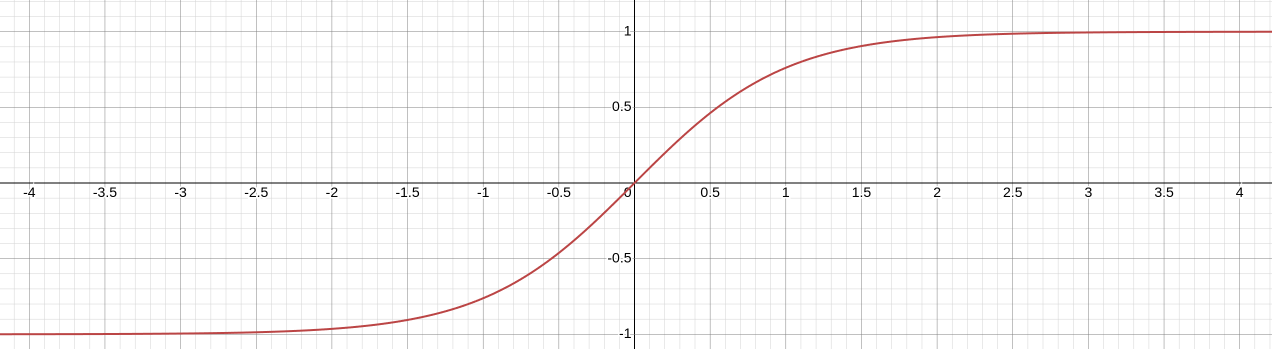
하이퍼볼릭 탄젠트 함수(Hyperbolic tangent function)은 위에서 소개한 시그모이드 함수와 유사한 형태를 지니지만, 출력값의 중심이 0이다. 또한, 출력값이 -1~1 범위를 가지므로, 시그모이드 함수에서 발생하지 않는 음수 값을 반환할 수 있다는 장점이 있다. 그래서 출력값은 더 넓고 다양한 형태를 활성화할 수 있고, 이는 곧 기울기 소실이 비교적 덜 발생한다는 것을 의미한다. 하지만, 시그모이드 함수와 마찬가지로, 입력값이 4보다 큰 경우, 출력값이 1에 계속 수렴하므로 동일하게 기울기 소실이 발생한다.

(2) ReLU 함수

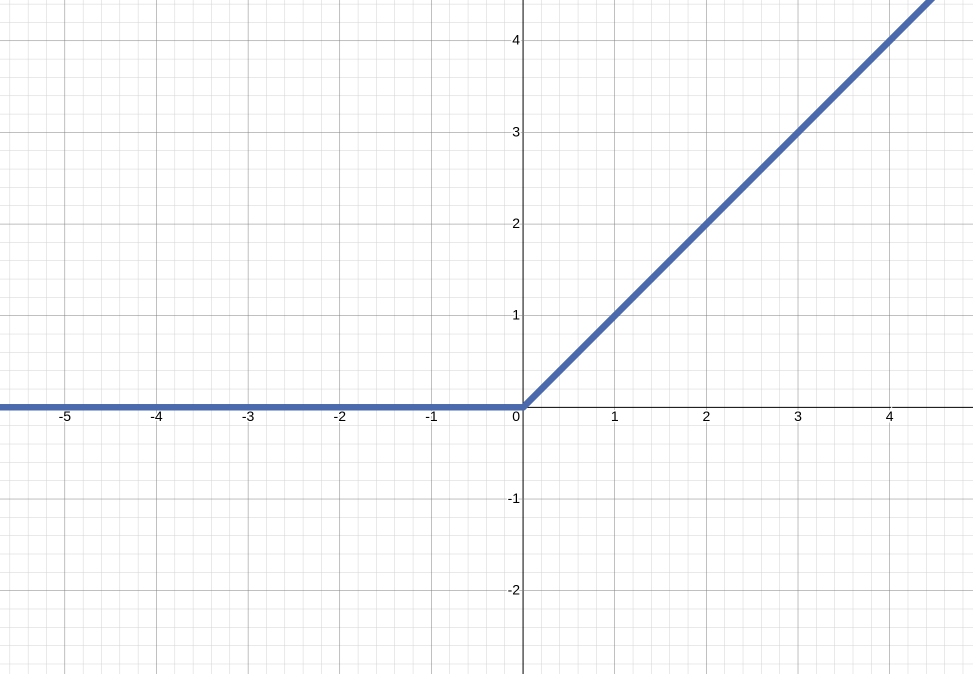
ReLU(x) = \begin{cases} x & if \; x > 0 \\ 0 & else: otherwise \end{cases}

ReLU (Rectified Linear Unit Function)는 0보다 작거나 같으면 0을 반환하며 0보다 크면 선형 함수에 값을 대입하는 구조를 갖는다. ReLU 함수는 선형 함수에 대입하므로 입력값이 양수라면 출력값이 제한되지 않아 기울기 소실이 발생하지 않으며, 수식 또한 매우 간단해 전파 과정에서 연산이 매우 빠르다는 장점이 있으나, 입력값이 음수인 경우 항상 0이어서 가중치나 편향이 갱신되지 않을 수 있다는 단점이 있다.

(3) PReLU

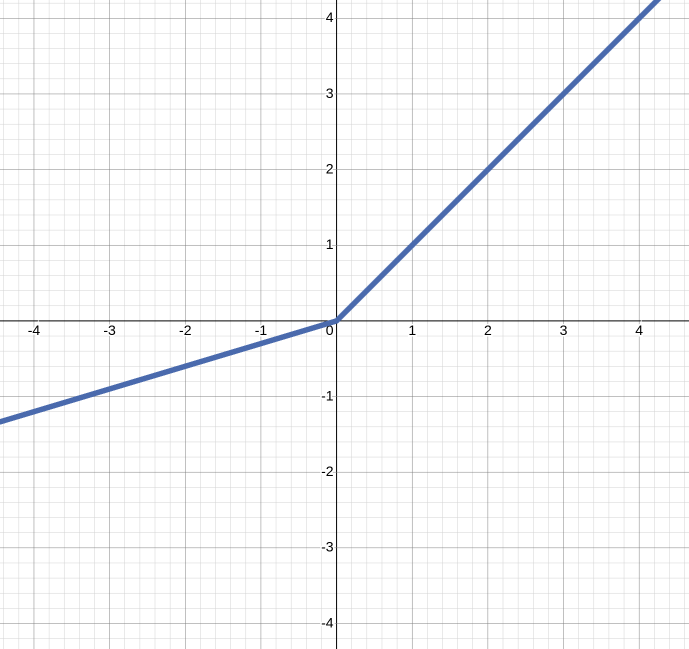
PReLU(x) = \begin{cases} x & if \; x > 0 \\ a \times x & else: otherwise \end{cases}

PReLU (Parametric Rectified Linear Unit Function)은 음수 영역의 기울기 값을 고정값이 아닌 학습을 통해 갱신되는 값으로 간주한다. ReLU를 사용할 때, 가중치의 합이 음수가 되면 해당 노드는 값을 갱신하지 않은 채로 남게되는데 이를 죽은 뉴런(Dying ReLU)라고 한다. 이를 방지하기 위한 함수 중 하나이다.

(4) ELU

ELU(x) = \begin{cases} x & if \; x > 0 \\ a \times (e^x -1) & else: otherwise \end{cases}

ELU (Exponential Linear Unit Function)는 지수 함수를 사용하여 부드러운 곡선의 형태를 갖는다. 기존 ReLU 함수가 x=0에서 끊어지는 형태를 가지는 것과 달리, 음의 기울기에서 비선형 구조를 가져 입력값이 0이 되는 경우에도 출력값이 급변하지 않아 경사 하강법의 수렴 속도가 비교적 빠른 장점이 있으나, 더 복잡한 연산을 진행하여 학습 속도 자체는 느려진다. 하지만 ELU 함수는 데이터의 복잡한 패턴과 관계를 학습하는 네트워크 능력을 향상시키는 데 도움이 될 수 있다.

(5) Softmax

p_k = \frac{e^{z_k}}{\sum^n_{i=1} e^{z_i}}

소프트맥스 함수는 차원 벡터에서 특정 출력값이 $k$ 번째 클래스에 속할 확률을 계산한다. 위 수식과 함께 설명하자면, $z_k$ 는 $k$ 번째 클래스에서 출력된 로짓(logit)이고 이를 지수화 함으로써 양수가 되고, 이를 전체 로짓의 exponential의 합으로 나누어 항상 0~1 사이로 매핑되게 한다. 클래스에 속할 확률을 계산하므로 은닉층이 아니라 출력층에서 사용되며 확률적 해석이 가능하다는 장점이 있지만, (클래스가 많다면) 계산 비용이 기본적으로 높은 함수이다.