NLP-Tutorial (5) 퍼셉트론

퍼셉트론

퍼셉트론(Perceptron)은 인공 신경망의 한 종류로, 신경 세포(Neuron)가 신호를 전달하는 구조와 유사한 방식으로 구현되었다.

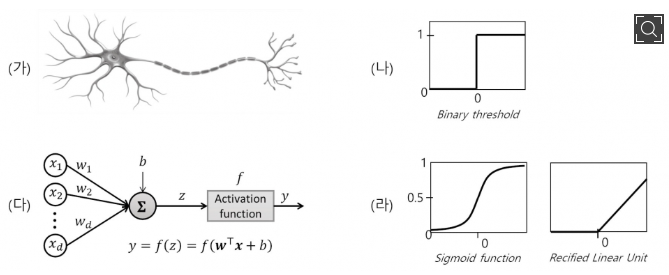신경세포를 모방한 퍼셉트론의 구조(출처 : 포항공대신문)

생물학적 신경망은 가지돌기(Dendrite)가 외부의 신경 자극을 받아 신경세포체에서 가중 압력을 받고 이를 기반으로 신호를 전달한다. 전달되는 신호는 축삭을 통해 다른 신경 세포로 최종 신호를 전달하고, 이때 시냅스(Synapse)라는 연결 부위를 통해 신호를 전달하며 세기도결정된다.

퍼셉트론도 이와 유사하다. 입력값을 받고 연산을 진행하여 임계값보다 크면 전달하고, 작으면 전달하지 않는다. 다시 말하자면, 퍼셉트론은 TLU(Threshold Logic Unit) 형태를 기본으로 하며, 계단 함수 형태의 함수를 적용하여 0과 1 사이 혹은 -1과 1사이 값을 출력하는 모델을 의미한다.

단층 퍼셉트론

단층 퍼셉트론(Single Layer Perceptron)은 하나의 계층을 갖는 모델을 의미한다. 입력을 통해 데이터가 전달되고 입력값은 각각의 가중치와 함께 노드에 전달되며, 입력값과 가중치를 곱한 값이 다시 활성화 함수에 전달된다. 활성화 함수에서 출력값이 계산되고, 이 값을 손실 함수에 실제값과의 차이를 활용해 가중치를 변경한다. 아래는 이 과정을 모델 구조로 시각화한 것이다.

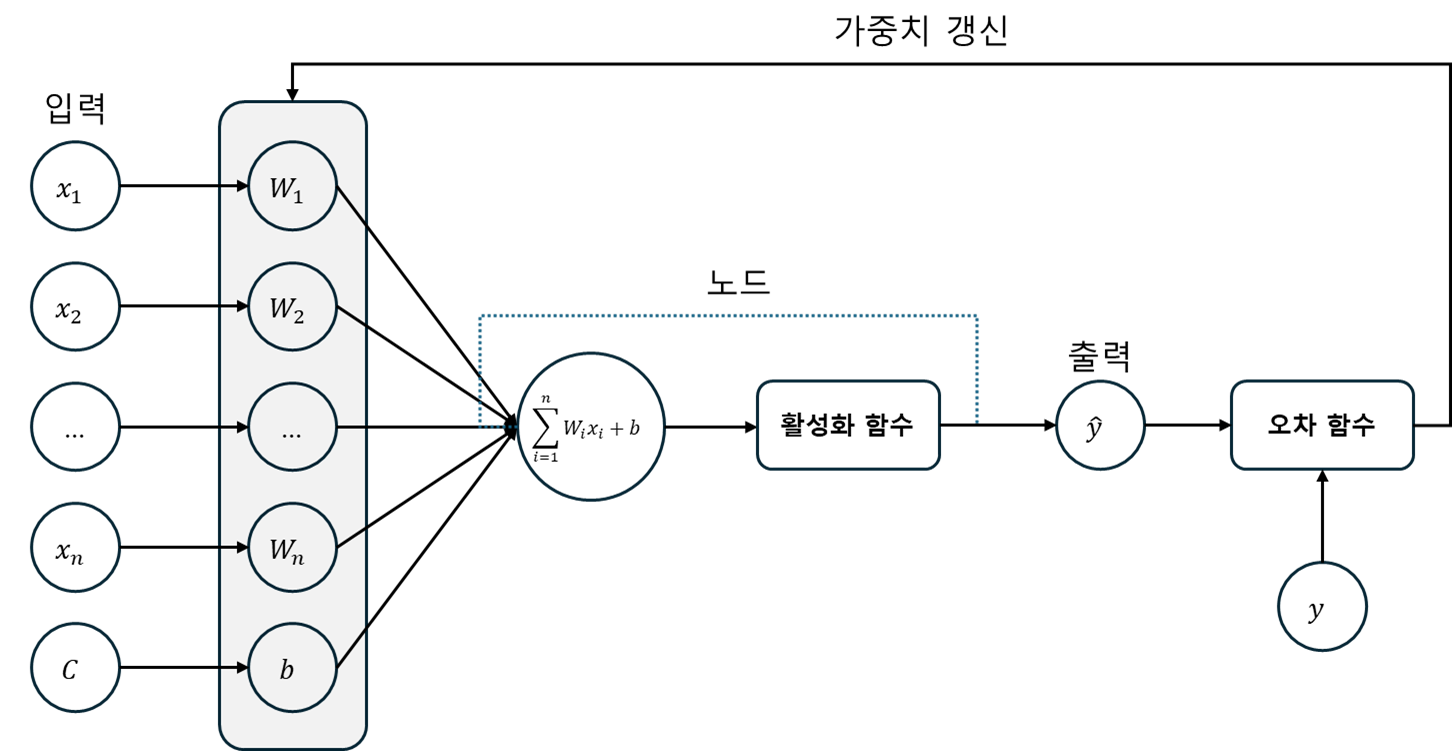
그러나, 단층 퍼셉트론 만으론 한계가 존재한다. 단층 퍼셉트론은 단순 AND, OR 게이트와 같은 구조는 쉽게 구현할 수 있다. 비유하자면, 단층 퍼셉트론 만으론 2차원 좌표계 상에 한 선을 긋는 것은 잘할 수 있다. 아래 예시처럼,

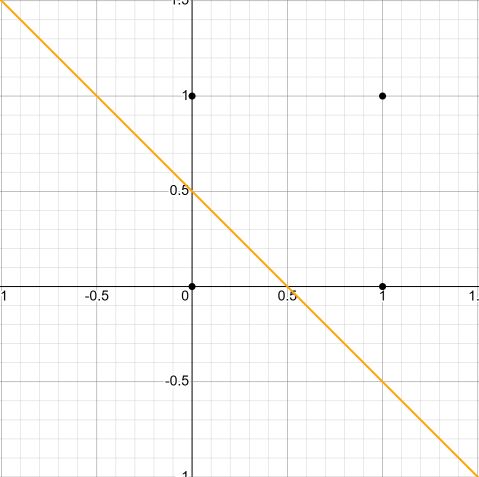
(0,0) (1,1) (0,1) (1,0) 네 점이 있고, OR 연산을 구현하면, (0,0)과 나머지로 분류할 수 있을 것이다. 이는 한 선만으로도 분류할 수 있다.

하지만 XOR 연산은 한 선으로 어떻게 구현할 수 있을까? (0,0)과 (1,1)이 같은 그룹으로 묶이고, (1,0)과 (0,1)이 묶여야 하는데, 한 선으론 할 수 없다. 최소 두 선이 필요하다.

이러한 문제를 위해, 우리는 다층 퍼셉트론을 활용한다.

다층 퍼셉트론

다층 퍼셉트론(Multi-Layer Perceptron, MLP)은 단층 퍼셉트론을 여러 개 쌓아 은닉층을 생성한다. 그리고 이 은닉층이 2개 이상 연결되면 우리는 비로소 심층 신경망(Deep Neural Network, DNN)이라 부른다. 은닉층이 늘어날수록, 더 복잡한 구조의 문제를 해결할 가능성이 크다.

단층 퍼셉트론 VS 다층 퍼셉트론 실습을 통한 비교

먼저 단층 퍼셉트론을 구현하고, XOR을 학습 시킨 뒤 제대로 모델이 생성되는지 확인해보자.

만약 XOR 데이터셋이 마땅히 없다면, 이걸로 생성한 후 진행한다.

import numpy as np
import pandas as pd

def generate_xor_boolean_csv(
    file_path: str,
    n_rows: int = 200,
    random_seed: int = 42
):
    """
    이 함수는 총 n_rows개의 행을 가진 CSV 파일을 생성합니다.
    - x1, x2: True 또는 False (무작위)
    - y: x1 XOR x2 결과 (True/False)
    Parameters:
        file_path (str): 생성할 CSV 파일 경로
        n_rows (int): 생성할 행 개수 (기본값: 200)
        random_seed (int): 난수 시드 (기본값: 42)
    """
    np.random.seed(random_seed)
    
    # x1, x2 무작위 Boolean 생성
    x1 = np.random.choice([False, True], size=n_rows)
    x2 = np.random.choice([False, True], size=n_rows)
    
    # XOR 결과
    y = np.logical_xor(x1, x2)
    
    # DataFrame 생성
    df = pd.DataFrame({
        'x1': x1,
        'x2': x2,
        'y': y
    })
    
    # CSV로 저장
    df.to_csv(file_path, index=False)
    print(f"CSV 파일이 생성되었습니다: {file_path}")

if __name__ == "__main__":
    generate_xor_boolean_csv("xor_boolean_data.csv")

이제 단층 퍼셉트론을 구현해보자.

import torch
import pandas as pd
from torch import nn
from torch import optim
from torch.utils.data import DataLoader, Dataset

class CustomDataset(Dataset):
    def __init__(self, csv_file):
        df = pd.read_csv(csv_file)
        self.x1 = df.iloc[:, 0].values
        self.x2 = df.iloc[:, 1].values
        self.y = df.iloc[:, 2].values
        self.length = len(df)

    def __getitem__(self, idx):
        x = torch.tensor([self.x1[idx], self.x2[idx]], dtype=torch.float32)
        y = torch.tensor(self.y[idx], dtype=torch.float32)
        return x, y

    def __len__(self):
        return self.length
      
class CustomModel(nn.Module):
    def __init__(self):
        super().__init__()
        self.layer = nn.Sequential(
            nn.Linear(2, 1),  # 입력 차원 2(데이터 특징 개수), 출력 차원 1
            nn.Sigmoid()
        )

    def forward(self, x):
        return self.layer(x)
      
train_dataset = CustomDataset("../xor_boolean_data.csv")
train_dataloader = DataLoader(train_dataset, batch_size=32, shuffle=True, drop_last=True)

device = "cuda" if torch.cuda.is_available() else "cpu"
model = CustomModel().to(device)
criterion = nn.BCELoss().to(device)
optimizer = optim.Adam(model.parameters(), lr=0.001)

for epoch in range(10000):
  cost = 0.0
  for x, y in train_dataloader:
      x, y = x.to(device), y.to(device)

      optimizer.zero_grad()
      output = model(x)
      loss = criterion(output, y.unsqueeze(1))  # y를 (batch_size, 1) 형태로 변환
      loss.backward()
      optimizer.step()

      cost += loss
      
  cost = cost / len(train_dataloader)
  
  if (epoch + 1) % 1000 == 0:
      print(f"Epoch [{epoch + 1}/10000], Cost: {cost:.3f} ")
      
with torch.no_grad():
  model.eval()
  
  inputs = torch.FloatTensor([[0, 0], [0, 1], [1, 0], [1, 1]]).to(device)
  outputs = model(inputs)
  
  print("XOR Predictions:")
  print(outputs)
  print(outputs <= 0.5)

class CustomModel(nn.Module):
    def __init__(self):
        super().__init__()
        self.layer = nn.Sequential(
            nn.Linear(2, 1),  # 입력 차원 2(데이터 특징 개수), 출력 차원 1
            nn.Sigmoid()
        )

단층이기에, 위처럼 단 하나의 레이어만 생성한다.

이제 이걸 실행하고 결과를 출력하면 아마

Epoch [1000/10000], Cost: 0.693 
Epoch [2000/10000], Cost: 0.693 
Epoch [3000/10000], Cost: 0.692 
Epoch [4000/10000], Cost: 0.693 
Epoch [5000/10000], Cost: 0.693 
Epoch [6000/10000], Cost: 0.694 
Epoch [7000/10000], Cost: 0.693 
Epoch [8000/10000], Cost: 0.692 
Epoch [9000/10000], Cost: 0.692 
Epoch [10000/10000], Cost: 0.693 
XOR Predictions:
tensor([[0.4896],
        [0.4910],
        [0.4786],
        [0.4800]], device='cuda:0')
tensor([[True],
        [True],
        [True],
        [True]], device='cuda:0')

이런 식으로 나올 것이다. Cost가 거의 일정히 유지되는 것을 볼 수 있는데, 이는 XOR 문제 자체를 단층으론 해결할 수 없다는 증거이다. 그리고, 테스트를 위해 모델의 값을 입력하여도 전부 True를 반환하여 제대로 분류하지 못함을 보여준다. 이제, 간단히 층을 하나만 추가해보자

class CustomModel(nn.Module):
    def __init__(self):
        super().__init__()
        self.layer1 = nn.Sequential(
            nn.Linear(2, 2),  # 입력 차원 2(데이터 특징 개수), 출력 차원 1
            nn.Sigmoid()
        )
        self.layer2 = nn.Sequential(
            nn.Linear(2, 1),  # 입력 차원 2(이전 레이어 출력), 출력 차원 1
            nn.Sigmoid()
        )

    def forward(self, x):
        x = self.layer1(x)
        x = self.layer2(x)
        return x

그리고 결과를 다시 보면

Epoch [1000/10000], Cost: 0.463 
Epoch [2000/10000], Cost: 0.368 
Epoch [3000/10000], Cost: 0.351 
Epoch [4000/10000], Cost: 0.356 
Epoch [5000/10000], Cost: 0.347 
Epoch [6000/10000], Cost: 0.357 
Epoch [7000/10000], Cost: 0.342 
Epoch [8000/10000], Cost: 0.345 
Epoch [9000/10000], Cost: 0.349 
Epoch [10000/10000], Cost: 0.344 
XOR Predictions:
tensor([[0.0083],
        [1.0000],
        [0.4784],
        [0.4784]], device='cuda:0')
tensor([[ True],
        [False],
        [ True],
        [ True]], device='cuda:0')

예상 못한 상황이 발생했다. Cost가 어느정도 내려가는 것은 맞으나, 결과가 좋지 않다. 이는 마침 다음 장에 다룰 내용과 연관 있으니, 다음 장에서 다루겠다.

결과 개선만 하자면, 위의 데이터셋 생성에서 200행 설정값을 400행까지 늘려보자. 그리고 그 데이터셋으로 다시 코드를 실행시켜보면

Epoch [1000/10000], Cost: 0.188 
Epoch [2000/10000], Cost: 0.003 
Epoch [3000/10000], Cost: 0.000 
Epoch [4000/10000], Cost: 0.000 
Epoch [5000/10000], Cost: 0.000 
Epoch [6000/10000], Cost: 0.000 
Epoch [7000/10000], Cost: 0.000 
Epoch [8000/10000], Cost: 0.000 
Epoch [9000/10000], Cost: 0.000 
Epoch [10000/10000], Cost: 0.000 
XOR Predictions:
tensor([[8.5054e-10],
        [1.0000e+00],
        [1.0000e+00],
        [7.1441e-10]], device='cuda:0')
tensor([[ True],
        [False],
        [False],
        [ True]], device='cuda:0')

아마 이런 식으로 결과가 나올 것이다. Cost가 0으로 수렴하였고, 주어진 문제를 정확히 분류해냈다. (참고로, 이 문제에선 괜찮지만, Cost가 0으로 조기 수렴하는 것이 마냥 좋은건 아니다. 다음 장에서 설명할 예정이다.)

그럼 아까 단층 퍼셉트론 문제에서도 데이터셋 늘리면 되는거 아니야? 라고 질문할 수 있으니 동일한 400행 데이터로 다시 단층 퍼셉트론을 실행시키면

Epoch [1000/10000], Cost: 0.689 
Epoch [2000/10000], Cost: 0.691 
Epoch [3000/10000], Cost: 0.690 
Epoch [4000/10000], Cost: 0.689 
Epoch [5000/10000], Cost: 0.689 
Epoch [6000/10000], Cost: 0.688 
Epoch [7000/10000], Cost: 0.688 
Epoch [8000/10000], Cost: 0.690 
Epoch [9000/10000], Cost: 0.689 
Epoch [10000/10000], Cost: 0.690 
XOR Predictions:
tensor([[0.5646],
        [0.5523],
        [0.4998],
        [0.4873]], device='cuda:0')
tensor([[False],
        [False],
        [ True],
        [ True]], device='cuda:0')

아니라는 것을 확인할 수 있다!