NLP Tutorial (6) - 과대적합과 과소적합

이로운·2025년 6월 21일

NLP_tutorial

목록 보기

6/8

과대적합(Overfitting)과 과소적합(Underfitting)

과대적합과 과소적합은 머신러닝 과정에서 자주 발생하는 문제다. 과대적합은 모델이 훈련 데이터에서는 우수하게 예측하지만, 새로운 데이터에 대해선 제대로 하지 못하는 경우를 말한다. 즉 모델이 훈련 데이터에만 적합하게 학습된 경우를 발한다. 과소적합은 반대로 훈련 데이터에 대해서도 성능이 안좋고, 새로운 데이터에서도 성능이 안좋은 말한다. 그림으로 나타내자면 아래와 같다. 과대적합의 경우, 그림과 함께 다시 말하자면, 학습 데이터에서만 너무 딱 맞게 학습이 되어, 그림과 같이 엄격히 구분하나 새로운 데이터에선 제대로 하지 못하는 것을 말한다.

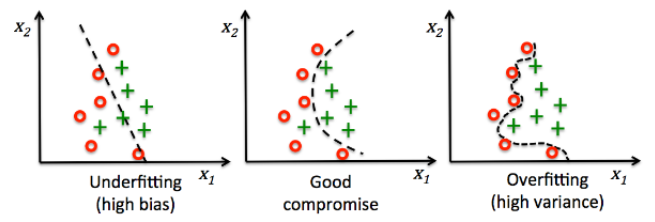
(이미지 출처 : https://opentutorials.org/module/3653/22071)

원인?

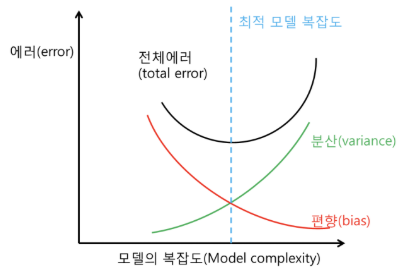(이미지 출처 : https://soobarkbar.tistory.com/21)

원인은 다양하다. 일단은 단순하게, 모델의 구조가 너무 단순해 제대로 학습 데이터의 특징을 살리지 못한 경우가 있다. 모델은 분산과 편향 간의 적절한 균형을 갖추어야 하는데, 분산이 너무 높으면 동일한 데이터에 대해서도 추정치에 대한 변동이 커지며, 편향이 커지면 추정치가 항상 일정된 값을 갖게될 확률이 높다. 모델이 복잡해질수록 분산은 커지고 편향은 작아지므로, 본인의 목적에 맞는 모델을 적절히 설계하는 것이 중요하다. 당연한 말이지만, 적절한 학습 데이터와 학습 횟수도 중요하다.

해결 방법

1. 데이터 수집

과대적합과 과소적합 모두 모델이 훈련 데이터를 제대로 학습하지 못하는 경우다. 과대적합은 훈련 데이터를 너무 적합하게 학습해 문제가 발생하고, 과소적합은 훈련 데이터를 제대로 학습하지 못해 발생한다. 따라서, 새로운 추가적 훈련 데이터를 준비하여 노이즈를 학습하지 않으면서 일반적인(General) 규칙을 찾을 수 있게 학습 데이터 수를 확보한다.

2. Feature engineering

신규 데이터 수집이 어렵다면, 기존 훈련 데이터에서 변수나 특징을 추출하여 Feature를 더 작은 차원으로 축소한다.

3. 배치 정규화

모델에 배치 정규화(Batch normalization)를 적용해 모델 성능과 안정성을 향상시킨다. 모델의 계층마다 평균과 분산을 조정해 내부 공변량 변화를 줄여 과대적합을 방지한다.

4. 가중치 초기화

가중치 초기화는 모델의 매개변수를 최적화하기 전에 가중치 초기값을 설정하는 과정을 말한다. 학습 시 기울기가 매우 작아지거나 커지는 문제를 발생할 수 있다. 적절한 초기 가중치를 설정하면, 과대적합 문제를 방지할 수 있다.

5. 정칙화(Regularization)

모델의 정칙화를 적용해 목적 함수에 패널티를 부과하는 방법이다. 모델을 일부 제한해 과대적합을 방지하며 정칙화에는 학습 조기 중단, L1 Regularization, L2 Regularization, Dropout 등이 있다.

하나씩 더 자세히 알아보자.

배치 정규화(Batch normalization)

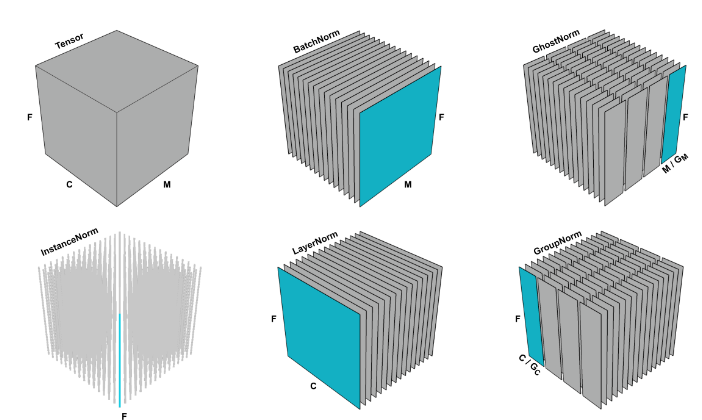
이미지 출처 : (https://velog.io/@osk3856/Batch-vs-Layer-Noramlization)

배치 정규화는 내부 공변량 변화(Internal covariate shift)를 줄여 과대적합을 방지하는 것을 말한다. 일반적으로, 학습할 때 입력값을 배치 단위로 나눠 학습을 진행하는데, 상위 레이어의 매개변수가 갱신될 때마다 현재 레이어에 전달되는 데이터의 분포도 변화한다.

각 계층은 배치 단위의 데이터로 인해 계속 변화되는 입력 분포를 학습해야 하기 때문에 신경망의 성능과 안정성이 낮아져 학습 속도가 느려진다. 이렇게 내부 공변량 변화랑 레이어마다 입력 분포가 변경되는 현상을 말한다. 변화가 발생하면 다음 은닉층으로의 전달값이 균일해지지 않아 가중치가 제대로 갱신되지 않고, 일정한 값으로 수렴하기 어려워지며 일반화가 어려워지며 느려진다. 반면 정규 배치화 적용 시 이미지 분류 모델에서 배치 정규화 적용 시 14배 더 적은 학습으로도 동일한 정확도를 달성할 수 있다는 장점이 있다.

상단의 그림은 배치 정규화 외에도 특징 맵을 3차원 시각화 했을 때 정규화가 수행되는 방식을 보여준다. 한 블록을 이미지나 텍스트 데이터라 한다면, 차원(F)은 이미지 데이터의 크기 혹은 어휘 사전의 크기를 말하고, 채널(C)의 경우 이미지 데이터의 채널이나 시간 간격을 의미한다.

배치 정규화는 위 그림에서 미니 배치(M)에서 계산된 평균 및 분산을 기반으로 레이어의 입력을 정규화하는 것을 말하며, 레이어 정규화는 이미지 데이터 전체가 아닌 채널별로 정규화 하는 것을 말한다. 배치 정규화는 일반적으로 CNN이나 MLP와 같은 문제를 다룰 때 사용한다.

계층 정규화는 미니 배치 단위가 아니라 채널 축으로 계산되는 방식을 말하고, 일반적으로 자연어 처리나 순환 신경망, 트랜스포머 기반 모델에서 주로 사용된다.

인스턴스 정규화는 채널과 샘플을 기준으로 정규화를 하며, 각 샘플에 대해 개별적으로 수행되므로 입력이 다른 분포를 갖는 작업에 적합하며 GAN이나 Style transfer 모델에서 주로 사용되고, 그룹 정규화는 채널을 N개의 그룹으로 나누고 정규화를 수행한다.

네 가지 방법 중 배치 정규화에 대해서만 간략히 수식으로 알아보자.

y_i = \frac{x_i - E[X]}{\sqrt{Var[X]+\epsilon}} * \gamma + \beta

$x_i$ 는 입력값을, $y_i$ 는 배치 정규화가 적용된 결과값이다. $E[X]$ 는 산술 평균을, $Var[X]$ 는 분산을 의미한다. $X$ 는 전체 모집단을 의미하며 이는 곧 미니 배치의 은닉층 출력값이다. $\epsilon$ 은 분모가 0이 되는걸 방지하고자 추가된 아주 작은 미소값이다.

그리고 여기서 $\gamma, \beta$ 가 학습 가능한 매개변수로, 활성화 함수에서 발생하는 음수의 영역을 처리할 수 있게 값을 조절하는 스케일(Scale) 값과 시프트(Shift) 값이다.

X_1 = [-0.6577, 0.7392, 0.2432]

X_2 = [-0.5797, 0.2145, 0.5662]

X_3 = [0.636, 1.523, 0.322]

텐서의 초기값이 이렇게 형성되었다고 하자. 먼저, $X_1$ 의 값에 배치 정규화를 적용해보자.

E[X] = (-0.6577 + 0.7392 + 0.2432) / 3 \eqsim 0.1082

Var[X] \eqsim 0.3343

이제 위에서 소개한 배치 정규화 수식을 적용하면 출력 $y_1$ 은 -1.3246이란 값을 출력할 것이다. 동일한 과정에 대해 모든 값을 정규화하면

Y_1 = [-1.3246, 1.0912, 0.2334]

Y_2 = [-1.3492, 0.3077, 1.0415]

Y_3 = [-0.3756, 1.3685, -0.9930]

이제, 코드 상의 결과와 비교해보자.

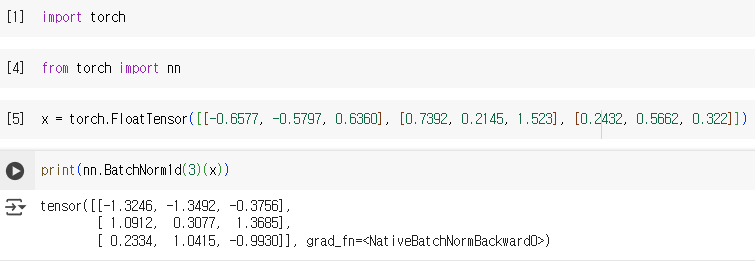
(평소엔 Ubuntu VScode 환경에서 작업하는데, 오늘은 윈도우 Colab에서 해보았다.)

위에서 계산한 결과와 일치함을 확인할 수 있다.

이렇게 값으로만 보면 "그래서 이 달라진 값이 뭘 의미하는데?"라고 할 수 있다. 그러나, 배치 정규화는 이런 간단한 과정만으로도 큰 힘을 발휘한다.

비유적으로 설명하자면, 공장의 조립라인과 비슷하다. 공장의 조립라인이 퀄리티 좋은 하나의 제품을 만들려면, 각 생산 라인에서 나온 결과물끼리 Fit하게 맞아 들어가야한다. 하지만, 어느날 출력물이 들쭉날쭉하다면, 결국 좋은 제품을 만들긴 쉽지 않을 것이고 시간도 오래 걸릴 것이다.

여기서 각 조립라인을 레이어, 결과물을 출력값, 그리고 제품 간의 일관성을 Internal Covariate Shift와 연계하여 생각하면, 이해가 될 것이다.

가중치 초기화

가중치 초기화는 모델의 초기 가중치 값을 설정하는 것을 말한다. 모델 매개변수에 적절한 초기값을 설정하면, 기울기 폭주/소실 문제를 방지할 수 있으며 수렴 속도 또한 향상시킬 수 있다. 가중치 초기화 방법엔 상수 초기화, 무작위 초기화, Xavier 초기화, Kaiming & He 초기화, 직교 초기화 등이 있으며, 이 중 Kaiming He와 직교 초기화에 대해서 소개한다.

카이밍 허(Kaiming He) 초기화
(여담이지만, 사람 이름이다.) 카이밍 허 초기화는 균등 분포나 정규 분포를 사용하여 가중치를 초기화 하는 방법이다.

W = \mathcal{U}(-a, a)

a = gain \times \sqrt{\frac{3}{fan_{in}}}

W = \mathcal{N}(0, std^2)

std = \frac{gain}{\sqrt{fan_{in}}}

카이밍 허 초기화는 현재 레이어의 입력 수( $fan_{in}$ )를 기반으로 각 노드의 출력 분산이 입력 분산과 동일하도록 가중치를 초기화한다. 일반적으로 카이밍 허 초기화 방법은 ReLU 계열 활성화 함수에서 사용되는데, ReLU가 입력 분산의 일부만 전달한다는 특성을 보정하여 깊은 신경망 구조에서도 출력 분산을 일정히 유지하게끔 하고, 이는 죽은 뉴런 문제를 최소화한다.

직교(Orthogonal) 초기화
직교 초기화는 SVD(Signular value decomposition)를 활용해, 자기 자신을 제외한 나머지 모든 열, 행 벡터와 직교이면서 동시에 단위 벡터인 행렬을 만드는 방법을 말하며, LSTM(Long short term memory), GRU(Gated Recurrent Units)와 같은 순환 신경망에서 자주 사용된다.

그 이유를 수식과 함께 살펴보자.

A ~ \mathcal(0,1)^{m \times n}

A = U\Sigma V^{\top}

W = \begin{cases} U_{:,1:n,} & m >= n \\ V_{:,1:m,} & m < n \end{cases}

W^{\top}W = I_n

$W$ 가 이렇게 결정되는데, RNN은 동일한 가중치를 여러 번 곱하기에, 행렬에 따라 기울기 소실(폭주) 문제가 심화된다. 반면 직교 초기화는 고유값이 모두 1인 직교 행렬을 사용해, 순(역)전파 시 신호 크기를 늘 보존한다.

정칙화

정칙화는 모델 학습 시 발생하는 과대적합 문제를 방지하기 위해 사용되는 기술로, 손실 함수에 패널티를 부여하는 방법이다. 과대적합은 모델이 학습 데이터를 통해 일반화된 것이 아닌 암기해버린 것으로, 데이터의 노이즈까지 학습할 때 발생한다. 정칙화는 이러한 노이즈에 강건하고 일반화된 모델을 구축하기 위해 사용하는 방법이다. 정칙화를 적용하면, 학습 데이터 내 작은 차이점에 대해 덜 민감해져 모델의 분산 값이 낮아진다. 종류에는 L1 Regularization (Lasso Regularization), L2 Regularization (Ridge Regularization), Dropout 등이 있다.

L1 Regularization
$L_1 = \lambda * \sum^n_{i=0} |w_i|$
이름에서도 알 수 있듯, L1 Norm ( $||X||_1$ ) 방식으로 정칙화를 한다. L1 놈은 벡터 또는 행렬값의 절대값의 합을 나타내는데, L1 정칙화는 손실 함수에 이 값을 추가하는데, 이러면 모델은 가중치 절대값의 합도 최소가 되는 방향으로 학습이 진행된다. 이는 곧, 모델 학습 시 값이 크지 않은 가중치들은 0으로 수렴하게 되어 예측에 필요한 특징 수가 줄어든다. 사용 시엔, 위 수식에서 $\lambda$ 로 정의된 규제 강도를 잘 설정해야 하는데, 0에 가까울수록 효과가 없고, 너무 크면 많은 특징을 0으로 만들어서 과소적합 문제에 노출될 것이다.
L2 Regularization
$L_2 = \lambda * \sum^{n}_{i=0} |w^2_i|$
L2 정칙화는 L2 놈을 이용하여 규제를 추가하는데, 방식은 L1 자체와 같다. 하지만, L2 놈은 하나의 특징만이 도드라지는 문제를 방지하는 것에 의미를 둔다. L2 정칙화는 L1 정칙화와 달리 가중치 값들을 0으로 만드는 것이 아니라, 모든 가중치를 작게 만들기 때문이다.
Dropout

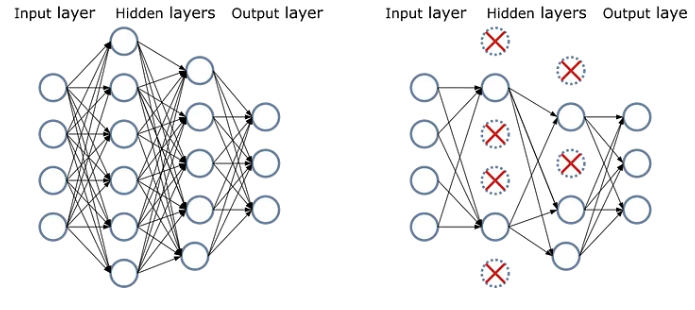
(이미지 출처 : https://vitalitylearning.medium.com/understanding-dropout-a-key-to-preventing-overfitting-in-neural-networks-21b28dd7c9b1)
드롭 아웃은 모델의 훈련 과정에서 위 그림처럼 일부 노드를 일정 비율로 제거하거나, 0으로 설정해 과대적합을 방지하는 방법이다. 과대적합을 발생시키는 이유 중 하나는 노드 간 동조화(Co-adaptation) 현상이다. 동조화란 모델 학습 중 특정 노드의 가중치나 편향이 큰 값을 갖게 되면 다른 노드가 그 값을 갖는 노드에 의존하게 되는 것을 말한다.
하지만, 모든 노드를 사용해 학습을 하지 않으므로 데이터세트의 크기가 크지 않다면 효과를 얻기 힘들며, 오히려 불균일한 학습을 일으킨다. 그러므로, 드롭아웃은 충분한 데이터셋과 깊은 모델일 때 사용하는 것이 탁월하다.