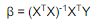1. LinearRegression(선형 회귀)란?
통계학에서 선형 회귀는 종속 변수 y와 한 개 이상의 독립 변수 X와의 선형 상관 관계를 모델링하는 회귀분석 기법이다. 한 개의 설명 변수에 기반한 경우에는 단순 선형 회귀, 둘 이상의 설명 변수에 기반한 경우에는 다중 선형 회귀라고 한다.
위키피디아 발췌
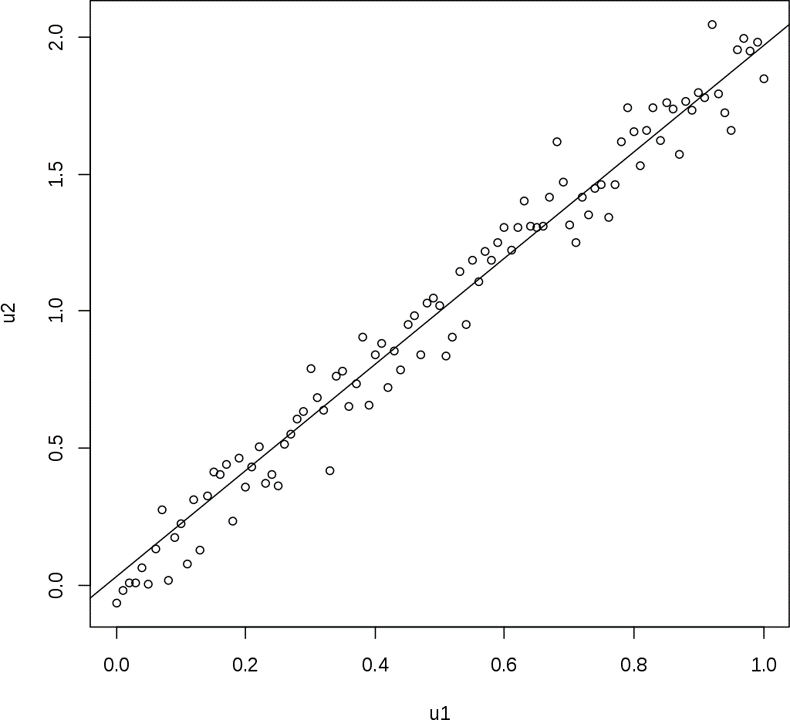
2. 회귀 분석
회귀 분석을 통해 상관계수를 넘어서 더 많은 정보를 얻을 수 있습니다.
기존 상관계수를 통해 두 연속형 변수의
- 관계 유무
- 관계 방향성
- 관계 강도
를 알 수 있었다면 회귀분석을 통해서는 추가적으로
- X(독립변수)를 이용해 Y(종속변수)를 추정할 수 있음
- X를 이용해 Y를(Y의 변동성) 설명할 수 있음.
2번 특징을 더 자세히 알아보면, Y의 개별 데이터가 모두 다를 때(변동성이 있을 때) 이 변동성을 X를 통해 설명할 수 있다는 의미입니다. X와 Y의 관계를 설명할 수 있다면, X를 통해 Y를 추정할 수 있으므로 사실상 1번과 2번은 같은 의미이며 어디에 초점을 두느냐에 따라 달라집니다.
정리하자면
- Linear Regression은 어떠한 독립 변수들과 종속 변수 간의 관계를 예측할때, 그 사이 관계를 선형 관계(1차 함수)로 가정하고, 모델링하는 지도 학습 알고리즘입니다.
- Linear Regression은 보통, 인자와 결과 간의 대략적인 관계 해석이나, 예측에 활용됩니다.
- Linear Regression은 확률 변수를 수학적 함수의 결과인 변수(모델링 결과값)으로 연결해준다는데, 그 의미가 큽니다.
- Linear Regression은 변수의 수에 따라, 다음과 같이 구분
- 선형 회귀 분석 : 변수 1개와 종속 변수 간의 선형 관계 모델링은 단순
- 다중 선형 회귀 분석 : 독립 변수 여러 개와 종속 변수 간의 선형 관계 모델링
3. 단순 선형 회귀 모델
위는 단순 선형 회귀의 수식으로,
: 독립변수
: 가중치(weight)
: 편향(bias)
으로 w와 b를 통해 x와 y는 다양한 직선을 표현할 수 있게 됩니다.
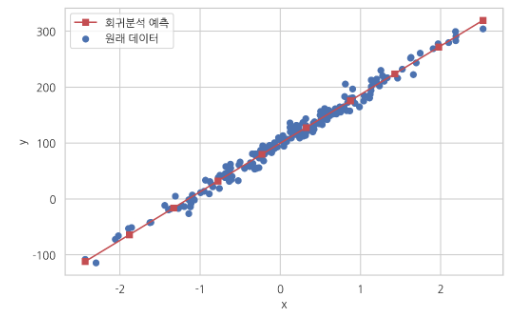
앞서 얘기했던 Y의 변동성을 X를 통해 설명하고자 한다면 적절한 w와 b를 선정해야 합니다. 그렇다면 가장 적절한 w와 b는 어떻게 선정할까요? 바로 오차, 학습, 평가를 통해 최적의 w, b를 선정할 수 있습니다.
오차
데이터에서 x와y의 관계를 w와 b를 이용하여 식을 세우는 일을 가설이라고 합니다. 이때 가설로부터 얻은 예측값의 오차를 계산하는 식을 세우고, 이 식의 값을 최소화하는 최적의 와 를 찾아냅니다.
이때 예측값에 대한 오차에 대한 식을 목적 함수(Objective function) 또는 비용 함수(Cost function) 또는 손실 함수(Loss function) 라고 합니다.
Linear Regression의 Residual(잔차)
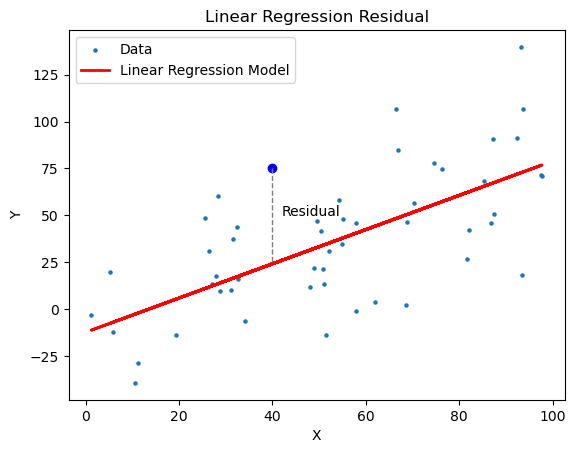
Linear Regression에서 종속 변수는 관찰의 결과인 확률변수이기 때문에, 오차(error)를 포함합니다. 오차를 알기 위해서는, 모델링을 위한 인자와 종속 변수 간의 모든 경우의 수를 학습해야하지만, 현실적으로 불가능하기에 Linear Regression에서는 오차를 사용하지 않고, 표본집단(학습데이터)으로 학습된 모델의 예측값과 실제 관측값 사이의 차이인 잔차(residual) 개념을 사용합니다.
Linear Regression 학습
이러한 잔차 값을 제곱하고 모두 더한 것을 잔차제곱합(RSS)라고 합니다.
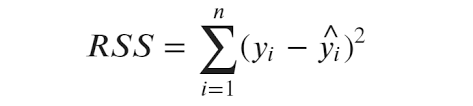
: i번째 데이터의 실제 종속 변수 값
: 데이터의 예측값
잔차 제곱합이 작다는 것은 실제 값과 회귀 모델로 예측한 값의 차이가 작음을 의미하며 오차가 작을수록 선형 회귀 모델이 데이터를 잘 표현한다고 볼 수 있습니다.
P.S. RSS의 평균을 Mean Squared Error (MSE)라고 하며, 이 또한 많이 사용됩니다.
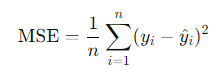
그렇기에 Linear Regression의 모델 추정을 위해서, RSS을 최소화하는 최소제곱법(OLS)을 사용합니다.
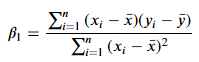
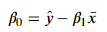
이 외에 기울기 하강법을 이용할 수도 있습니다.
Linear Regression 평가
평가를 위해서는 결정계수(coefficient of determination) 개념을 활용합니다.
결정 계수는 회귀 분석에서 모델이 얼마나, 실제 데이터를 잘 예측하는지를 나타내는 지표입니다.
- SST (Total Sum of Squares): 종속 변수 y와 그 평균값 ȳ 간의 차이를 제곱하여 모두 더한 값
- SSR (Residual Sum of Squares) : 종속변수 y에서 모델 추정값 간 차이를 제곱하여 모두 더한 . (잔차의 총합)
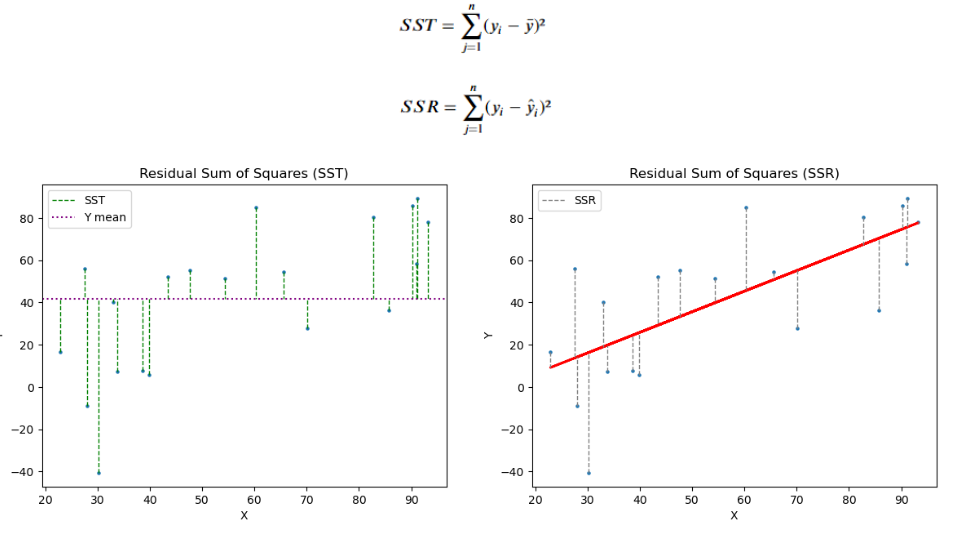
- : 결정 계수
- 결정 계수는 전체 오류(분산 개념) 중, 모델로 설명 가능한 오류의 범위의 비중을 뺀 비중으로, 1에 가까울수룩 일반적으로 예측력이 좋다고 해석합니다.
- 결정 계수가 대략적인 모델의 적합성을 파악할 수 있지만, 절대적인 지표는 아닙니다.
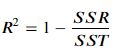
3. 다중 선형 회귀 모델
집의 매매 가격(종속변수)이 위치, 방의 개수 등 다양한 요인(독립변수)들로 결정된다면 이를 다중 선형 회귀 분석이라고 합니다.
다중 선형 회귀 분석에서는 최소제곱법을 이용하여, 회귀 계수 행렬을 다음과 같이 추정할 수 있습니다.