앞으로의 여정
공부를 하면서, 이번년도가 지나가기 전에 내가 하고싶었던 프로젝트를 꼭 완성하고싶다는 생각이 갑자기 들었다. 내가 하고 싶은 프로젝트는 pixel2style2pixel로 사람 얼굴 -> 애니메이션 과 애니메이션 -> 사람 얼굴로 바꾸는 필터를 만드는 것과 MuseGAN을 이용하여 AI로 노래를 만드는 것이다. 그래서 이번 글에서는 이 두 프로젝트를 진행하기 위해서 가장 기본이 되는 Generative Adversarial Networks(GAN)을 리뷰해보도록 하겠다. GAN 논문의 이름은 "Generative Adversarial Nets"이다.
생성(Generative),적대적(Adversarial)??
이 GAN이라는 네트워크에서는 두 개의 모델이 있는데, 바로 생성자(Generator)와 판별자(Discriminator)이다. 생성자와 판별자의 관계는 화폐 위조자와 위조 화폐를 탐지하려는 경찰로 표현할 수 있다.

생성자와 판별자의 관계를 위조자와 경찰로 표현한 그림
화폐 위조자가 처음에는 돈을 제대로 위조하지 못해 경찰이 위조 지폐를 쉽게 구분하지만, 가면 갈수록 더욱 화폐 위조자의 기술이 발전하여 지폐를 위조한다. 화폐 위조자는 진짜 같은 위조 지폐를 만들어 경찰을 속이고(Generator), 경찰은 진짜 지폐와 위조 지폐를 구분하기 위해 노력한다(Discriminator). 생성자와 판별자가 대립하며 학습이 진행하기 때문에 Generative(생성적) Adversarial(적대적)이라는 이름을 쓴것이다. 그렇다면 궁금한 점이 생긴다. 판별자의 모델은 우리가 많이 배워온 분류 모델이라 특별한게 없을 것 같은데, 생성자의 모델은 무엇일까??
Adversarial Net
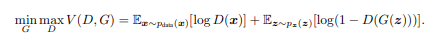
위의 수식은 GAN 모델 손실함수의 수식이다.
생성자(Generator)
D(Discriminator)는 G(Generator)가 만든 가짜 이미지에는 0을 출력하고 진짜 데이터는 1을 출력해야한다. G는 D가 G가 만든 가짜 이미지에 대해 1을 출력하게 해야하는데, G는 D가 데이터를 얼마나 잘 구분하는 지는 상관 없기 때문에 위의 수식에서 아래 그림의 부분은 제외해도 상관이 없다.
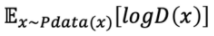
하지만 D(G(z))는 1이 출력이 되게 해야한다. 왜냐하면 G(z)는 G가 만든 가짜 이미지이고, D(G(z)) = 1이 된다는 것은 D가 G가 만든 가짜이미지에 잘 속아 넘어갔다는 것을 의미하기 때문이다. 그런데 여기서 의문점이 든다. D(G(Z)) = 1이 되면 log(1-1) = log0이 된다는 것인데 고등학생인 나는 log를 배운적은 있어도 log0은 처음본 것 같았다! 그래서 구글링을 해보았더니 log0은 정의되지 않았거나 음의 무한대라는 사실을 알게 되었다. 아하! 그렇다면 G의 목적은 V(D, G)가 최소가 되도록 해야하기 때문에 G가 원하는 결과가 나온다는 사실을 알 수 있다.
판별자(Discriminator)
D는 G가 만든 가짜 이미지에는 0을 출력하고 진짜 데이터에는 1을 출력해야 한다. 그래서 D(x) = 1이 나와야하고, D(G(Z)) = 0이 나와야한다. 그렇다면 log1이 된다. 엥? log1은 0이 아닌가?? 0이 왜 최대지?? 나도 처음에는 0이 왜 최대인지 궁금했었다. x값이 0~1이기 때문에 log1의 값이 최대라는 사실!! 그래서 D가 원하는 최적의 상황은 logD(x)나 log(1-D(G(Z)))의 값이 모두 0이 되는 것이다. 그래서 D는 0에 가까운 숫자로 가는 것을 MAX라고 하고, G는 최대한 낮은 숫자로 가야하기 때문에 MIN이라 수식에 적혀있는 것이다.
학습 방법
뭐...판별자야 우리가 그동안 공부해온 많은 모델이 판별자이니 그렇다 쳐도, 생성자를 결합한 network를 어떻게 학습시키냐에 대한 궁금증이 있었다. 논문에서는 2개의 망을 번갈아 가며 학습시키는 방법을 권장하였는데, 생성자(G)를 고정시킨 상태에서 K만큼 D를 학습시키며 다음은 판별자(D)를 고정시킨 상태에서 G를 훈련시켜 내쉬 평형 상태에 이를 때 까지 반복하는 방법이다.
내쉬 평형(Nash Equilibrium)
존 내쉬(John Forbes Nash, Jr)
미국의 천재 수학자 존 내쉬(1928~2015)가 발표한 게임이론의 중추적인 개념으로 존 내쉬는 이 공로를 인정받아 노벨 경제학상을 수상한다. 내쉬 평형은 각자가 상대방(경쟁자)의 대응에 따라 최선의 선택을 하고, 자신의 선택을 바꾸지 않는 균형상태를 말한다. 더욱 더 자세한 이론은
게임이론과 내쉬균형에 자세히 나와있다.
그래서 GAN에 내쉬 평행 이론이 나오는 까닭이 무엇이냐면 G와 D가 서로의 판단을 고려하여 최적을 하는 상태에 와야 G가 제대로 된 이미지를 생성한다고 할 수 있기 때문에 내쉬 평형에 이를 때까지 반복을 하는 것이다. 이런 평형상태에 이를 때 까지 반복하는 K는 실험자가 실험을 해가면서 결정을 해야한다.
마무리
내 목표의 첫단추를 꿰맬 수 있어서 기쁘고, GAN의 부족한 점을 보완해서 GAN에서 파생된 많은 모델들이 나를 기다리고 있다고 하니 기쁘기도하고 두렵기도 하다. 더욱 더 노력하는 인공지능 개발자가 되어야겠다고 다짐했다.


