[AI] Gradient Descent(경사하강법)

정의

경사하강법(Gradient Descent)은 1차 근삿값 발견용 최적화 알고리즘이다. 기본 개념은 함수의 기울기(경사)를 구하고 경사의 절댓값이 낮은 쪽으로 계속 이동시켜 극값에 이를 때까지 반복시키는 것이다.
wikipedia.org

경사하강법에 대한 아주 직관적인 예시를 들어보자면 이렇다. 당신이 하늘도 보이지 않을만큼 울창한 숲을 헤메고 있다고 했을 때, 가장 높은 산 봉우리에 오르고 싶다면 어떻게 해야할까? 답은 간단하다. 눈에 보이는 곳에서 가장 가파른 경사를 오르다 보면, 언젠가 가장 높은 산봉우리에 오를 수 있을 것이다. 물론 이 경우는 경사상승법(Gradient Ascent)이고, 하강법은 반대로 가장 낮은 곳을 찾아가는 과정이다.

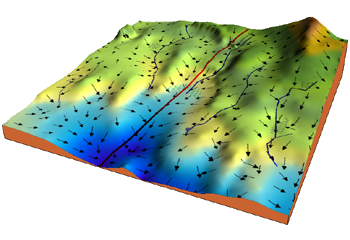
이미지 출처 : ML Glossary

머신러닝에서 쓰이는 이유

우리는 보통 함수의 최솟값을 찾고자 할 때, 미분계수를 구함으로써 찾곤 한다(컴퓨터를 사용하는 것이 아닌 그냥 수학 문제를 풀 때). 컴퓨터에서 해당 방법을 사용하지 않는 이유는 다음과 같다.

• 실제 분석에서(특히, 딥러닝 알고리즘을 활용하는 경우) 보게 되는 함수들은 형태가 굉장히 복잡해서 미분계수와 그 근을 계산하기 어려운 경우가 많음
• 미분계수 계산 과정을 컴퓨터로 구현하는 것보다, 경사하강법을 구현하는 것이 훨씬 쉬움
• 데이터의 양이 매우 큰 경우 경사하강법과 같은 순차적인 방법이 계산량 측면에서 훨씬 효율적

공식 유도

경사하강법은 함수의 기울기(=gradient)를 이용해서 함수의 최소값 일 때의 $x$값을 찾기 위한 방법이다. 기울기가 양수인 경우는 $x$ 값이 증가할수록 함수 값도 증가하고, 반대로 음수인 경우에는 $x$ 값이 증가할수록 함수 값이 감소한다. 그리고 기울기 값이 크다, 기울기가 가파르다는 것은 최소값으로부터 거리가 멀다는 뜻이다.

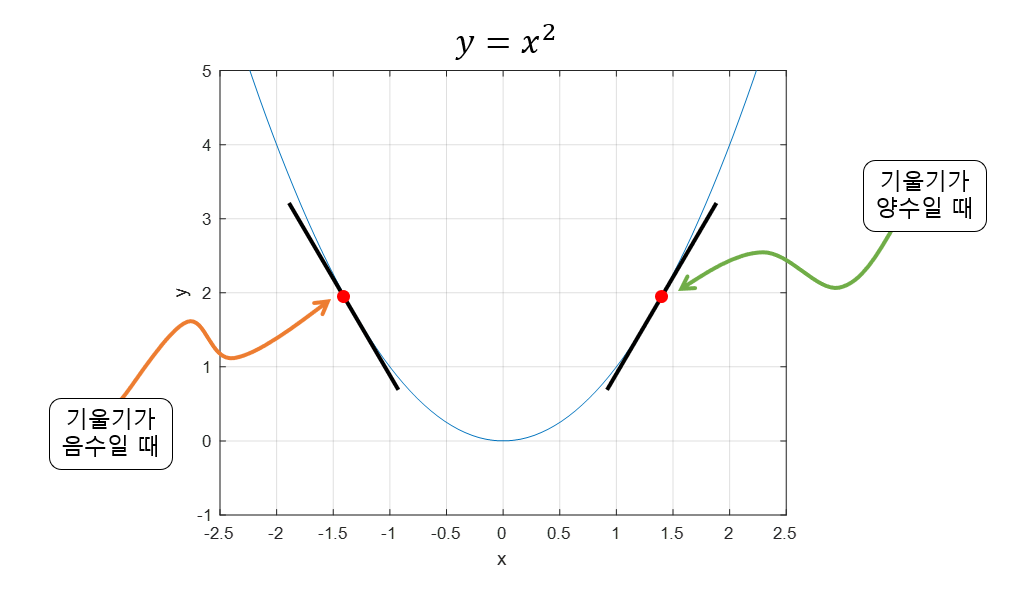
이미지 출처 : 공돌이의 수학정리노트

이 점을 이용해서 기울기가 양수라면 음의 방향으로 $x$를 옮기면 되고, 기울기가 음수라면 양의 방향으로 $x$를 옮기면 된다.

• 이를 공식으로 옮기면 다음과 같다.
  $(1)\qquad x_{i+1} = x_i - 이동거리 \times 기울기의\space부호$
  
  

식 (1)에서 기울기의 부호는 알 수 있지만, 이동 거리는 어떻게 구해야 할까?
미분 계수(=기울기=gradient)는 극소값에 가까워질수록 값이 작아진다. 따라서, 이동거리에는 미분 계수와 비례하는 값을 이용한다. 그럼 극소값에서 멀 때는 많이 이동하고, 극소값에 가까울 때는 조금씩 이동할 수 있다.

• 이렇게해서 유도되는 최종 공식은 다음과 같다.
  $(2)\qquad x_{i+1} = x_i - \alpha\frac{df}{dx}(x_i)$

  $\alpha=step\space size(hyperparameter)$

Step size(= $\alpha$)

적절한 step size 선택은 매우 중요하다. Step size가 큰 경우 이동 거리가 커지므로 빠르게 수렴할 수 있다는 장점이 있지만, 최소값으로 수렴되지 못 하고 함수값이 발산할 여지가 있다.
한편, step size가 너무 작으면 발산하지는 않겠지만, 최소값을 찾는데 너무 오래 걸릴 여지가 있다.

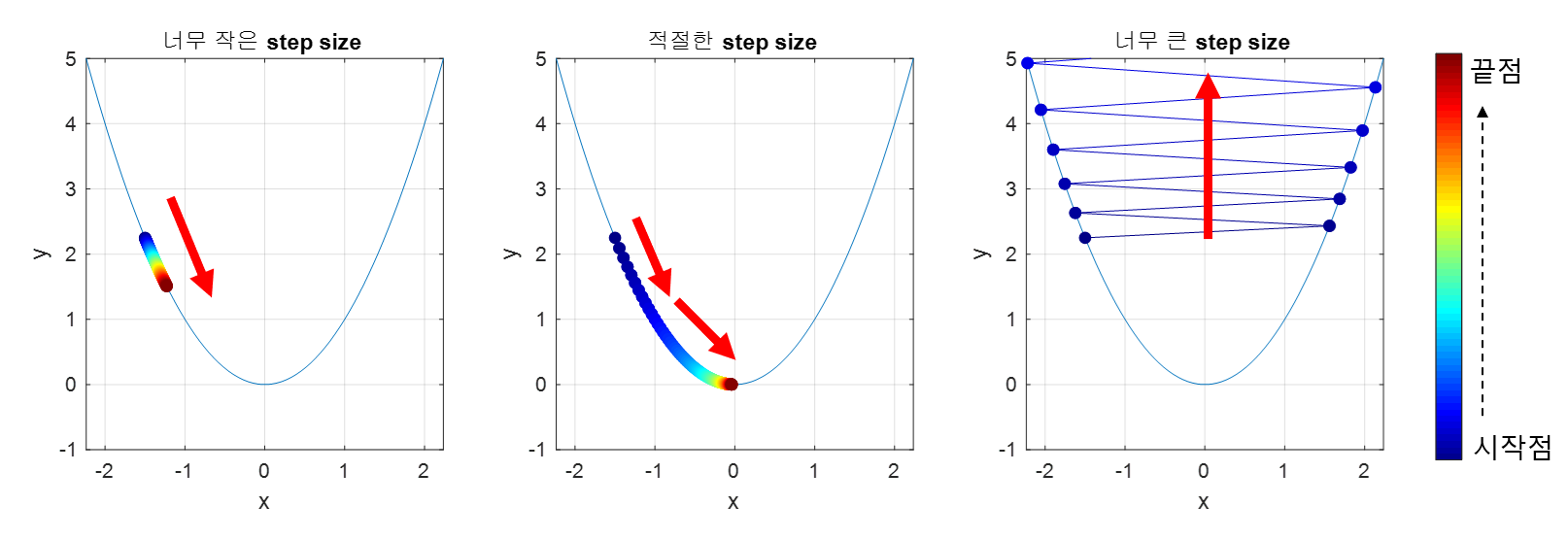
이미지 출처 : 공돌이의 수학정리노트

Local minima

경사하강법의 또 다른 문제는 local minima이다. 우리가 찾고 싶은 건 global minima(함수 전체에서의 최소값)이지만, 어떤 경우에는 local minima에 빠져 벗어나지 못 하는 상황이 발생한다.

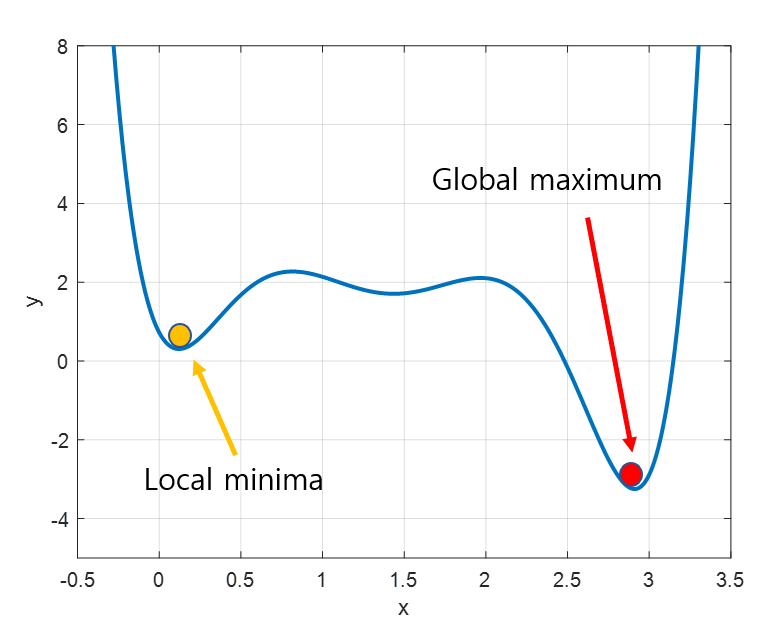
이미지 출처 : 공돌이의 수학정리노트

하지만 최근에는 실제로 딥러닝이 수행될 때, local minima에 빠질 확률이 거의 없다고 한다.
위의 그래프는 가중치(w)가 1개인 모델이지만 실제 딥러닝 모델에서는 w가 수도 없이 많고, 그 수 많은 w가 모두 local minima에 빠져야 w 업데이트가 정지된다. 이론적으로 거의 불가능에 가까운 일이므로, 사실상 local minima는 고려할 필요가 없다는 것이 중론이다.