
모델이 학습 데이터에 과적합되는 현상은 모델의 일반화 성능을 떨어트리는 주요 원인이다. 이번 포스팅에서는 과적합을 막는 몇가지 방법들에 대해서 알아보고자 한다.
1. 데이터 규모
데이터 규모가 작은 경우, 모델은 작은 규모의 데이터에 대해서 모든 특징(패턴, 노이즈 등)을 학습해버리기 때문에 쉽게 과적합 현상이 발생할 수 있다. 그러므로 데이터 규모를 늘려서 과적합 현상을 피해야 된다.
만약, 데이터의 양이 적은 경우에는 일반적으로 데이터에 대해서 증강(Augmentation)을 적용한다. 여기서 증강이란, 기존 데이터에 대해서 약간의 변형을 줄 수 있는 처리를 수행하는 것을 의미한다. 예를 들어, 노이즈를 추가하거나 이미지 데이터의 경우에는 Flip, Crop, Histogram Equalization 등이 있고, 자연어의 경우에는 번역 후 재번역을 통해 새로운 데이터를 만드는 역번역(Back Traslation)등이 있다.
2. 모델 규모
일반적으로 모델의 규모(깊이, 너비)가 클수록 과적합 현상의 발생 확률이 높다. 왜냐하면, 모델의 규모가 크다는 의미는 결국 모델의 저장 용량이 크다는 의미이고, 이는 데이터에 대해서 모두 학습할 가능성이 높다는 의미이기 때문이다. 따라서, 모델의 규모(Capacity)를 줄이는 것이 과적합 현상을 방지하는데 도움이 될 수 있다.
3. 가중치 규제(Regularization)
모델의 규모가 작다는 의미는 저장할 수 있는 가중치(파라미터)가 적기 때문에 높은 성능을 기대하기 어렵다. 이와 반대로 모델의 규모가 크면 위에서 언급한 것과 같이 과적합 문제가 발생한다. 가중치 규제(Regularization)은 복잡한 모델에 대해서 과적합 문제를 피하기 위해 사용하는 방법이다.

가중치 규제는 크게 L1 Regularization과 L2 Regularization이 있다. 여기서, λ는 Regularization의 정도를 결정하는 하이퍼 파라미터이다. 만약, λ의 값이 크다면 해당 항은 모델의 학습보다는 규제에 중점을 둔다는 의미로 해석할 수 있다. 왜냐하면, λ가 매우 크면 해당 항의 가중치는 0이거나 0에 매우 가까운 값이어야하기 때문이다.
한편, 위의 두 규제 식을 보면 공통적으로 손실 함수를 최소화하면서 가중치의 값들이 작아져야 한다. 즉, 가중치는 손실 함수를 최소화하도록 최적화 되면서, 가중치들의 절대 값 합 또한 최소여야 된다. 이에 따라 특정 가중치들은 0이거나 0에 가까운 값들을 가질 확률이 높다. 이 의미는 해당 가중치와 연결된 Feature(특성)는 중요하지 않다는 뜻이다.
L2 Regularization은 L1과 달리 가중치들의 제곱 합을 최소화하므로 가중치 값이 0보다는 0에 가까운 값들을 가지는 경향이 있다. 이에 따라 일반적으로 L1 Regularization은 어떤 Feature가 유용한 지 판단할 때 주로 사용하고, 실제 학습하는 상황에선 L2 Regularization이 주로 사용된다.
Regularization은 정규화란 뜻도 있지만, Machine Learning에서는 정규화는 주로 Normalization으로 표현한다. 이와 관련해서, 추후에 언급할 Batch Normalization, Layer Normalization 등이 있다.
4. 드롭 아웃(Dropout)
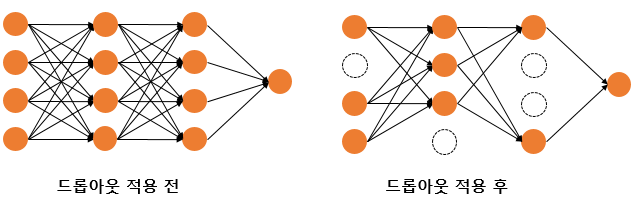
드롭 아웃은 쉽게 말해서 학습하는 동안 랜덤으로 모델 레이어의 일부 노드를 사용하지 않는 것을 의미한다. 단, 실제 추론(Inference)시에는 모델의 모든 레이어를 사용한다.
학습 시에 일부 레이어의 노드들을 랜덤으로 사용하지 않기 때문에 특정 노드의 가중치들이 집중되는 것을 막을 수 있고, 앙상블의 효과 또한 가질 수 있게 되면서 과적합을 막을 수 있게 된다.



