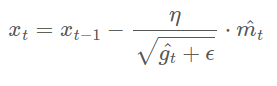옵티마이저(Optimizer)는 손실 함수의 결과값을 최소화 할 수 있는 최적화된 파라미터를 찾는 알고리즘을 의미한다. 역전파(Backpropagation)를 수행한 뒤, 손실 함수에 대한 각 파라미터(가중치)의 편미분 값을 이용한 식(옵티마이저)을 통해 파라미터를 최적화한다.

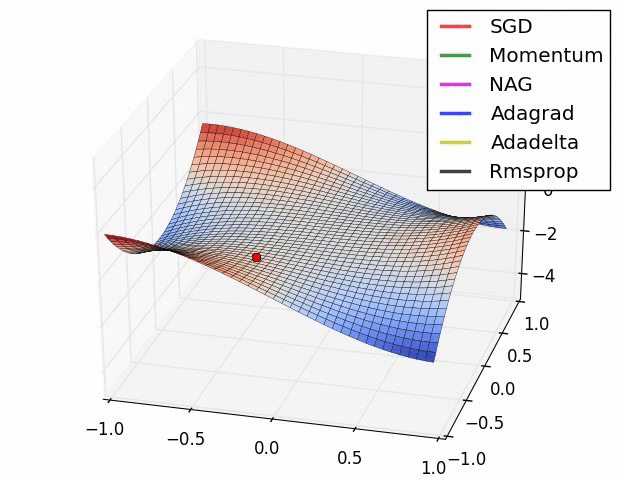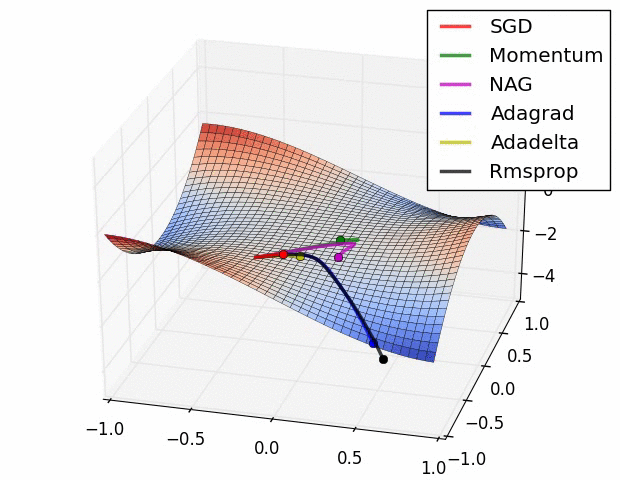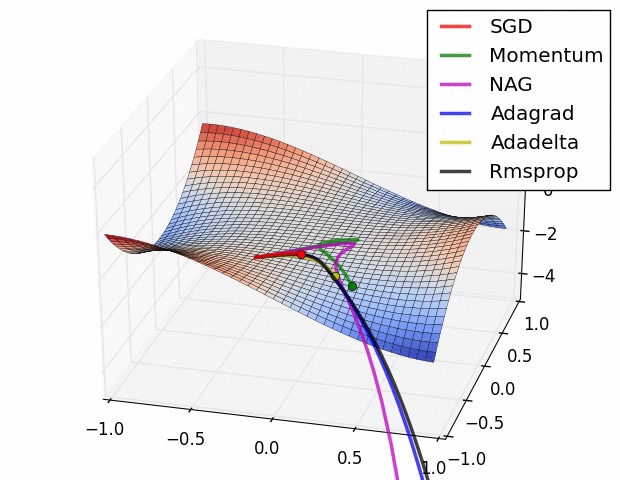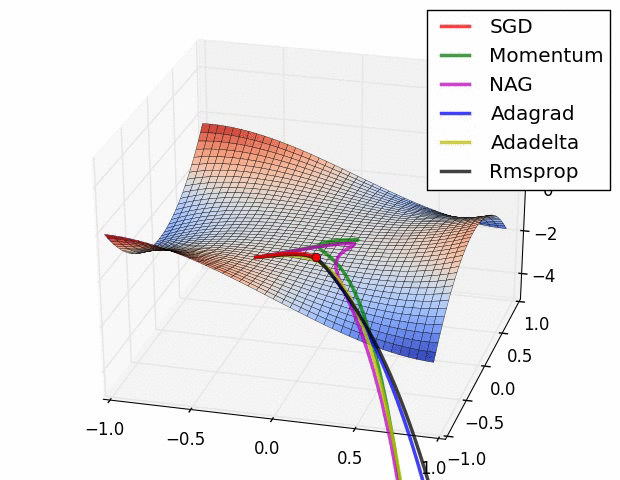
위와 같이 손실 함수의 그래프에 대해서 옵티마이저의 종류에 따라 모델의 최적화하는 과정이 달라지게 된다. 각 옵티마이저의 어떤 특성으로 인해 이러한 차이가 발생하는지 이번 포스팅에서 알아보고자 한다.

---

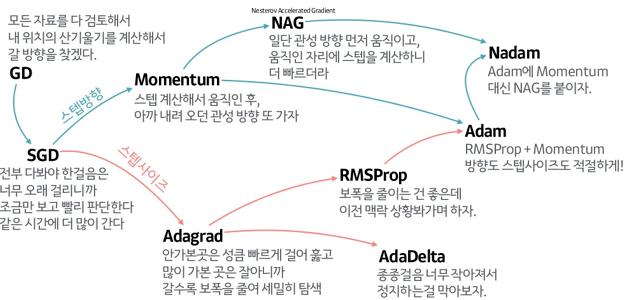
1. GD(Gradient Descent)

GD는 경사하강법으로도 불리며, 가장 기본이 되는 Optimizer이다. Loss Function에 대한 각 가중치(파라미터)의 기울기(Gradient)를 점점 감소하는 방향으로 업데이트하여 극솟값을 찾는다.

식은 다음과 같다.

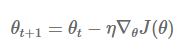
머신러닝 문제들은 대부분 비선형(non-linear)의 열린 형태(open form) 함수로 해결해야 된다. 또한 닫힌 형태(closed form)의 함수로 문제를 해결할 수 있다고 해도 수 많은 파라미터로 인해 학습하는 시간이 매우 오래 걸린다. 따라서, 한번에 머신러닝 문제를 해결할 수 있는 함수를 정의하기 어려우므로 옵티마이저들은 대부분 Step별로 가중치들을 업데이트한다.

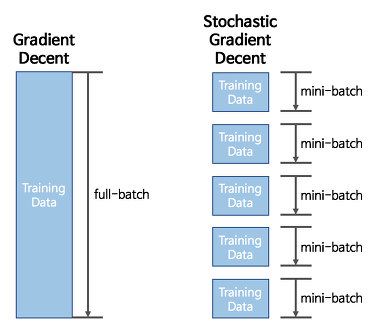
한편, 경사하강법은 데이터 셋 전체에 대해서 Loss Function을 계산하고 역전파를 통해 가중치를 업데이트 해야되기 때문에 데이터 셋의 크기가 큰 경우에는 학습 시간이 오래걸리는 문제점이 있다.

---

2. SGD(Stochastic Gradient Descent)

SGD는 전체 데이터셋을 탐색하지 않고, Mini Batch 단위로 데이터 셋을 탐색하여 가중치를 업데이트한다. 이로 인해 GD에 비해 가중치 업데이트 속도가 더 빠르고 학습 시간이 단축되는 장점이 있다.

한편, 경사 하강법은 다음과 같은 상황들로 인해 학습하는 과정에 문제가 발생할 수 있다.

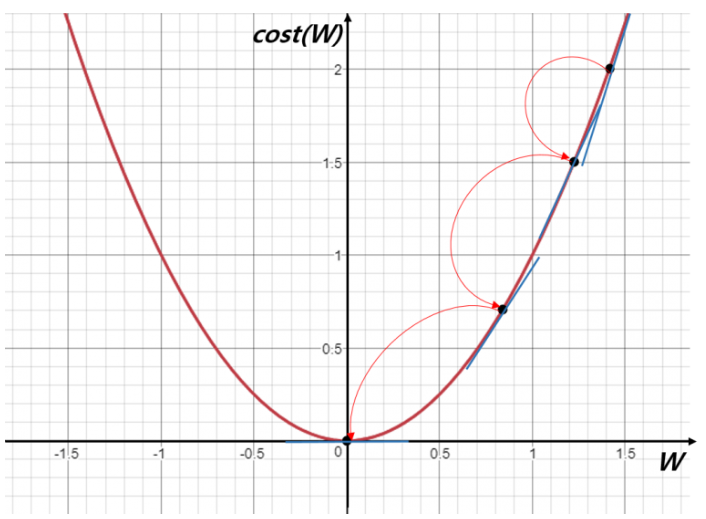
1. Local Mumimum

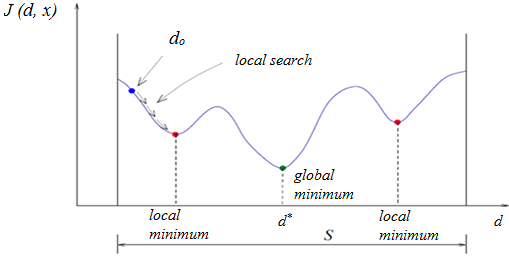
경사 하강법은 예를 들어 위와 같은 상황에서 local minimum에 수렴하고 가중치가 학습되지 않아서 global minimum을 찾지 못하고 최적 가중치를 얻지 못하게 된다.

2. Saddle Point

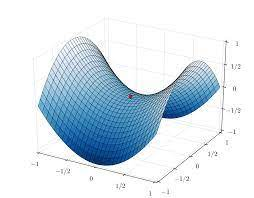
또한 위와 같이 Saddle Point 상황에서는 가중치의 업데이트 위치에 따라 극솟값이 극댓값으로 처리되어 가중치의 업데이트가 더 이상 진행되지 않는 문제점이 발생한다.

---

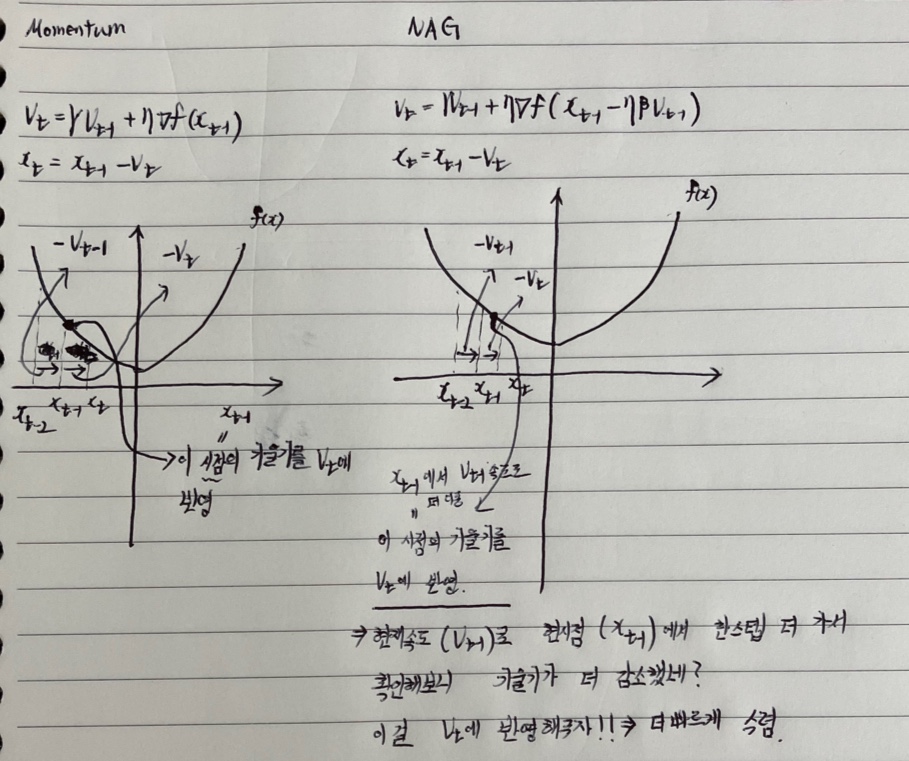
3. Momentum

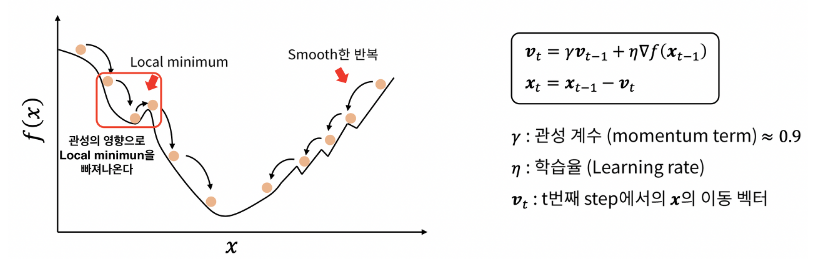
Momentum은 SGD에 관성 개념을 포함시킨 옵티마이저이다. 이전 Step에서의 가중치 이동벡터를 가중치 업데이트에 반영함으로써 손실 함수의 기울기가 0에 수렴하는 Local Minimum으로부터 벗어날 수 있게 된다.

단, 이동 벡터 $v_{t}$가 포함되면서 메모리가 추가적으로 필요하게 된다.

---

4. NAG(Nesterov Accelerated Gradient)

NAG는 Momentum을 응용한 방법으로, 다음 Step의 관성을 현재 지점($x_{t}$)의 기울기가 아닌 현재 관성을 통해 이동한 지점($x_{t}$-$\gamma \beta v_{t}$)의 기울기를 보고 결정하는 방식이다. 이 방법을 통해 다음 지점의 기울기 변화를 파악하고 다음 Step의 관성($v_{t+1}$)을 조절할 수 있게 된다.

---

5. AdaGrad(Adaptive Gradient)

AdaGrad는 학습의 진행 정도에 따라 학습률을 조율하는 옵티마이저이다. $g_{t}$는 누적해서 가중치의 기울기 제곱을 더해서 얻은 값이다. 학습을 진행할 수록 $g_{t}$값이 커지면서 학습률이 낮아지고 가중치의 변화량이 줄어들면서 세밀한 학습이 가능해진다.

단, $g_{t}$의 경우 한번 값이 커지면 계속해서 커지기 때문에 학습을 오래 진행하게 되면 학습률이 0에 점점 수렴하여 학습이 이뤄지지 않는 문제점이 있다.

---

6. RMSProp

RMSProp는 AdaGrad의 Learning Rate 제어 문제를 해결하기 위해 제안된 방법이다. 먼저, AdaGrad에서는 t-1 Step까지의 모든 Gradient를 제곱하여 더해줬지만, RMSProp은 지수이동평균(EMA, Exponential Mean Average)를 적용하면서 사용할 Gradient 수를 특정 window 사이즈인 w로 제한하여 Learning Rate 값을 제어했다.

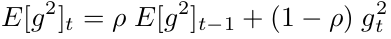
여기서, E는 기댓값을 의미하고 이는 곧 확률 평균을 의미한다.

---

7. AdaDelta

AdaDelta도 AdaGrad의 문제를 개선하기 위해 제안된 방법이다. 저자는 AdaGrad의 두 가지 문제를 지적했다.

1. Learning Rate 제어

2. Hyperparameter Learning Rate

AdaDelta는 Learning Rate 제어를 하기 위해 RMSProp과 동일하게 분모에 지수이동평균을 적용했다. 여기서, E는 확률 평균을 의미하고 기울기들의 제곱 합 형태로 표현되므로 저자는 RMS로 간략하게 표현했다.

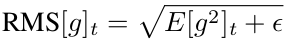
이를 통해 다음과 같이 가중치 업데이트 값을 구할 수 있다.

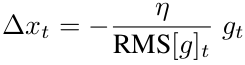
한편, 논문의 저자는 기존 SGD, Momentum, AdaGrad와 같은 옵티마이저들은 손실 함수에 대한 가중치 기울기와 가중치 단위가 서로 맞지 않다고 주장했다.

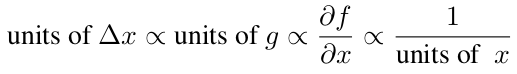
이와 대조적으로 Hessian 행렬을 사용하는 Neton's method과 같은 Second Order Method들은 가중치 x에 맞는 unit을 가진다고 주장했다.

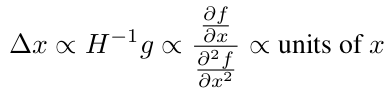
이로부터 위에서 언급한 가중치 업데이트 값의 형태로 수식을 맞추기 위해 식을 다음과 같이 수정했다.

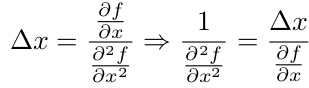
최종적으로 AdaDelta는 다음과 같이 가중치 업데이트 값을 얻을 수 있고, 이 값을 $x_{t}$에 더해줌으로써 가중치를 업데이트한다.

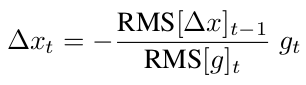
결국 AdaDelta는 Hyper Parameter Learning Rate를 사용하지 않아도 되는 장점이 있게 된다.

---

8. Adam(Adaptive Moment Estimation)

Adam은 딥러닝에서 가장 보편적으로 사용되는 옵티마이저로써, Momentum과 RMSProp을 합친 개념이다.

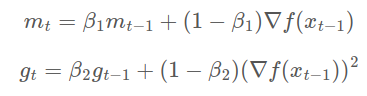
$m_{t}$와 $g_{t}$는 각각 Momentum과 RMSProp 개념에 관한 Adam 수식이다. Momentum 식에서 $m_{t-1}$와 Gradient간의 지수이동평균을 계산하여 $m_{t}$를 구하는 부분이 부분이 약간 수정되었다. 여기서, $\beta_{1}$과 $\beta_{2}$는 각각 0.9, 0.999로 설정했을 때 좋은 결과를 얻었다고 저자가 밝혔다.

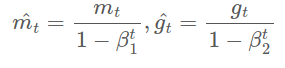
처음 학습을 시작할때는 $m_{t-1}$와 $g_{t-1}$의 값은 0이므로 $m_{t}$값과 $g_{t}$값은 Gradient에 각각 (1-$\beta_{1}$)와 (1-$\beta_{2}$)가 곱해진 값으로 업데이트 방향이 결정된다. 이 때, (1-$\beta_{1}$)와 (1-$\beta_{2}$)는 작은 값이기 때문에 $m_{t}$와 $g_{t}$ 값이 0이 될 확률이 높다. 이에 따라 학습이 진행되지 않는 문제가 발생한다. 이를 방지하기 위해 위의 식을 통해 초깃값이 0으로 편향되는 문제를 보정한다. 또한, 학습이 어느 정도 진행되면 t 값이 커지면서 1-$\beta^{t}$ 값이 1에 가까워지면서 이 보정 효과를 제어할 수 있다.

최종적으로 보정된 Momentum과 RMSProp값을 적용하여 위와 같이 가중치 업데이트 식을 구할 수 있다. 여기서, 저자는 학습률을 0.001로 설정했을 때 좋은 성능을 얻었다고 밝혔다.