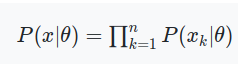1. 우도란?

일반적으로 우도(가능도, Likelihood)는 관측값이 어떤 모수로부터 나왔는지에 대한 적합성을 평가하는 측도이다.

모수와 관측된 확률변수를 각각 $\theta$와 $x_{k}$로 표현하면, 우도 함수는 다음과 같이 일반화 할 수 있다. 여기서, $x_{k}$는 같은 확률분포에서 독립된 확률변수를 나타내므로 각 우도의 곱으로 표현할 수 있다.

---

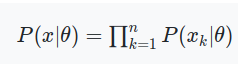
2. 최대 우도 추정

최대 우도 추정(Maximum Likelihood Estimation)은 파라미터 $\theta$ = ($\theta_{1}$, ..., $\theta_{m}$)와 확률변수이자 표본 데이터 x = ($x_{1}$, ..., $x_{n}$)으로 구성된 확률밀도 함수 P(x | $\theta$)에서 최댓 기댓값(우도)을 나타내는 파라미터 $\theta$를 찾는 방법을 의미한다.

여기서, 손실함수로 정의하기 위해 우도 함수에 대해서 다음 두가지 연산을 추가로 적용했다.

1. log

1) 가우시안 분포나 베르누이 분포 식은 지수 함수 형태로 존재한다. 이는 연산량의 증가를 유발하게 된다. 따라서, 로그를 분포 식에 적용하면 지수 항이 상쇄하게 되어 일반 다항식 형태로 표현하여 단순화 시킬 수 있다.

2) 우도 함수는 확률의 곱 형태로 구성되어 있다. 확률은 항상 1보다 작은 값이므로 연쇄적으로 곱하게 되는 경우 우도가 매우 작은 값이 되어 언더플로우 현상이 발생하게 된다. 따라서, 로그 연산을 적용하여 곱이 아닌 우도의 합 형태로 구성하여 언더플로우 문제를 해결할 수 있다.

2. negative

최대 우도 추정은 결국 최대 우도를 얻을 수 있도록 하는 파라미터를 구하는 방법이므로 모델은 우도 값이 최대가 되도록 학습한다. 따라서, 손실함수의 형태로 표현하기 위해 negative를 취해서 최소화 문제로 변형한다.

---

3. Negative Log Likelihood 활용

Negative Log Likelihood를 손실함수로 사용하는 경우에 우도함수를 특정 확률분포로 정의하여 사용하여 분류, 회귀 등의 Task에 자유롭게 적용할 수 있다.

3.1 회귀

3.2 이진 분류

3.3 다중 분류

---

4. KL-Divergence와 우도

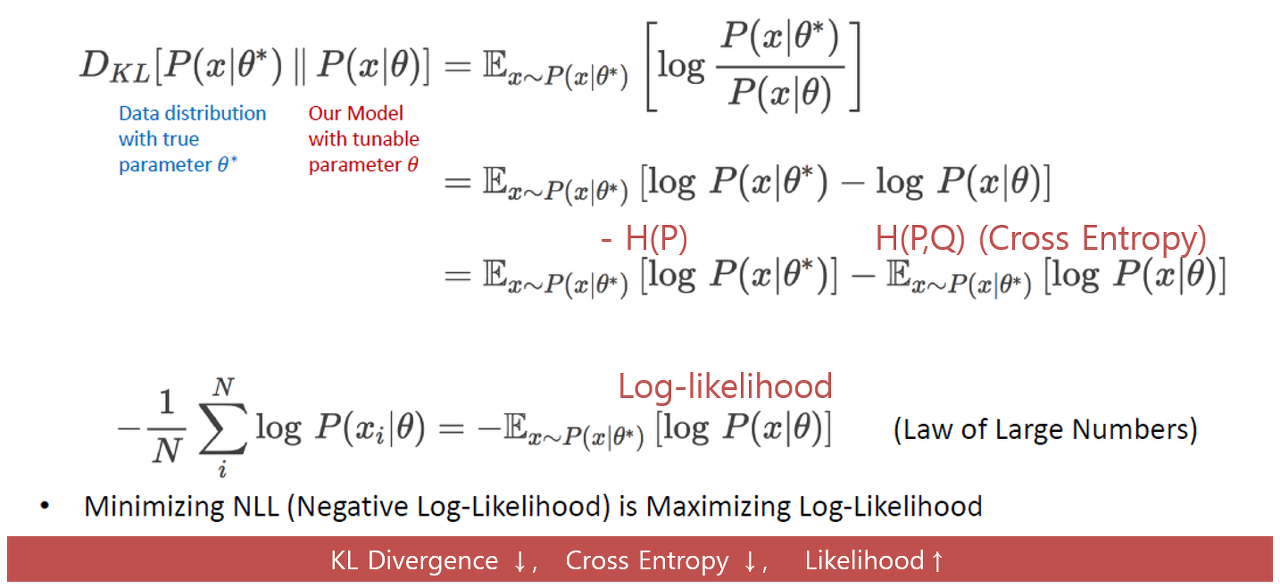
우도는 앞서 포스팅했던 KL-Divergence에 적용할 수 있다. KL-Divergence 식에서 확률분포를 우도 함수로 정의하고 식을 전개하면, Cross Entropy를 Negative Log Likelihood에 관한 수식으로 구할 수 있게된다. 따라서, Negative Log Likelihood를 최소화하게 되면, Cross Entropy 값은 작아지고, KL Divergence 값 또한 줄어들면서 최적 파라미터 $\theta$로부터 이상적인 확률분포를 얻을 수 있다는 점이다.