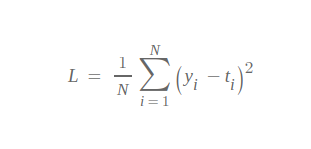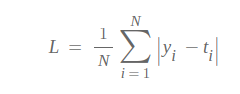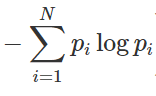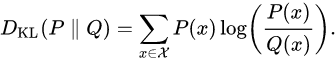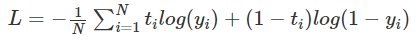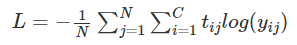손실 함수란, 실제 값과 모델 예측값 사이의 오차를 계산하는 함수이다. 인공지능은 손실 함수를 계산하여 이 값을 최소화하는 방향으로 학습하게 되므로 모델 학습에서 중요한 역할을 한다.
1. MSE(Mean Square Error)
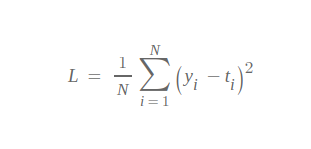
MSE 함수는 회귀(Regression)에서 흔히 사용되는 손실 함수이다. 여기서, N은 데이터 수에 해당하고 , 는 각각 실제 값과 모델 예측값을 의미한다.
2. MAE(Mean Absolute Error)
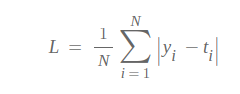
MAE 함수 또한 회귀(Regression)에서 흔히 사용되는 손실 함수이다. 식은 MSE 함수와 유사한데, 실제 값과 모델 예측값 사이의 Error를 계산하기 위해 제곱이 아닌 절대값을 취한다는 차이점이 있다.
3. Cross Entropy
3.1 정보량(Information)
정보이론에서는 확률이 낮을수록, 어떤 정보일지 불확실하다고 표현하며 이때 '정보가 많다' 혹은 '엔트로피가 높다'고 표현한다. 여기서, 정보량은 불확실한 정도를 의미하고 f(x) = -logP(x)으로 표현할 수 있다.
예를 들어, 어떤 사건의 확률이 매우 높다고 가정하면 우리는 실제로 이 사건이 발생했을 때 크게 영향을 받지 않는다. 이와 반대로 어떤 사건의 확률이 매우 낮은 상황에서 사건이 발생하면 우리는 크게 영향을 받게 되고, 훨씬 유용한 정보를 우리에게 제공하게 된다. 이로 인해 정보량은 확률에 반비례하다고 볼 수 있다.
3.2 엔트로피(평균 정보량, Entropy)
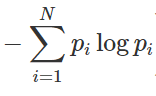
엔트로피는 어떤 상태에서의 '불확실성' 또는 어떤 사건이 발생했을 때 얻을 것으로 기대되는 '평균 정보량'을 의미한다.
3.3 KL-Divergence(Kullback Leibler Divergence)
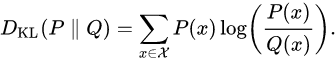
KL-Divergence는 상대 엔트로피라고 부르기도 하며, 하나의 확률분포 P가 다른 기준 확률 분포 Q와 얼마나 다른지를 측정한 통계적 거리의 한 유형이다.
또한 KL-Divergence는 어떠한 확률분포 P가 있을때, 그 분포를 근사적으로 표현하는 확률분포 Q를 P 대신 사용할 경우에 발생하는 엔트로피 변화를 의미한다. 따라서, 원래 확률분포 P가 가지는 엔트로피 H(P)와 확률분포 Q로 변경시에 발생한 엔트로피 H(P,Q)의 차로 표현하면 다음과 같다.
확률분포 Q를 이상적 확률분포 P로 근사화하는 과정을 모델이 학습하는 과정으로 표현할 수 있다. 그리고 위의 수식으로보면 를 최소화하는것은 Cross Entropy를 최소화 하는것과 같으므로 Cross Entropy를 Loss Function으로 사용할 수 있다.
3.4 BCE(Binary Cross Entropy)
BCE는 이진 분류기에서 주로 사용되는 Loss Function이다. BCE는 2개의 클래스에 대한 Loss를 계산하는데, 특정 하나의 클래스 확률은 1-다른 클래스 확률과 같기 때문에 다음 식으로 표현할 수 있다.
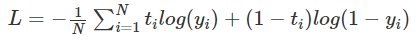
BCE는 멀티레이블 분류에도 사용되는데, 여기서 멀티레이블이란 여러 클래스가 중복으로 존재하는 경우를 의미한다. 즉, 하나의 대상에 대한 예측 결과가 1인 클래스가 여러개로 존재할 수 있고, 각 클래스 별 확률이 서로 독립적이므로 Activation Function은 Sigmoid를 사용한다.
3.5 Cross Entropy
Cross Entropy는 멀티 클래스 분류에 주로 사용되며 식은 다음과 같다.
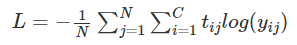
여기서 N과 C는 각각 데이터 수와 클래스 수를 의미한다. 각 클래스 별 확률이 서로 종속적이므로 Activation Function은 Softmax를 사용한다.
Vision AI Engineer