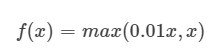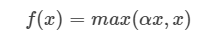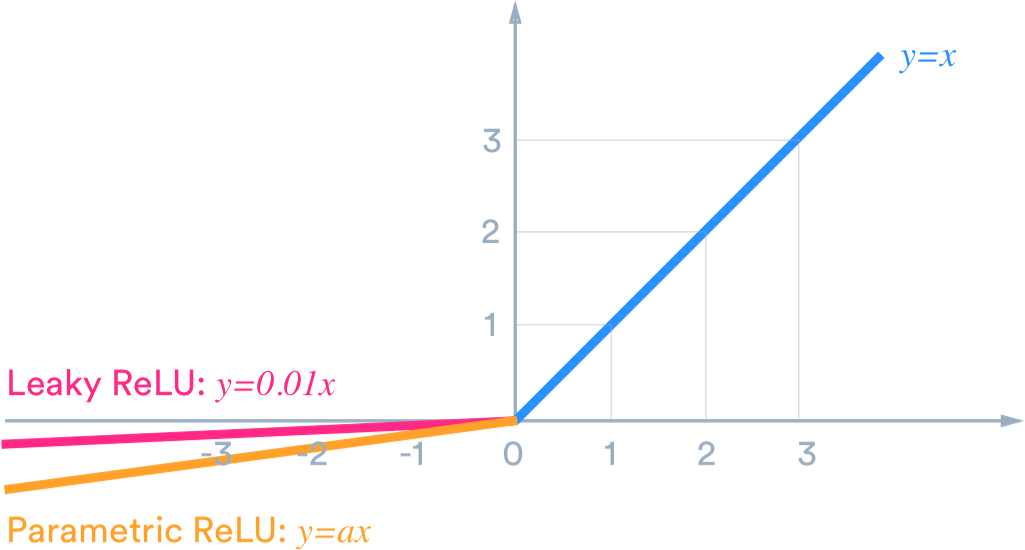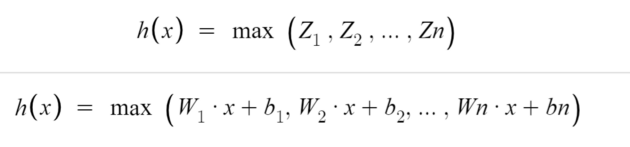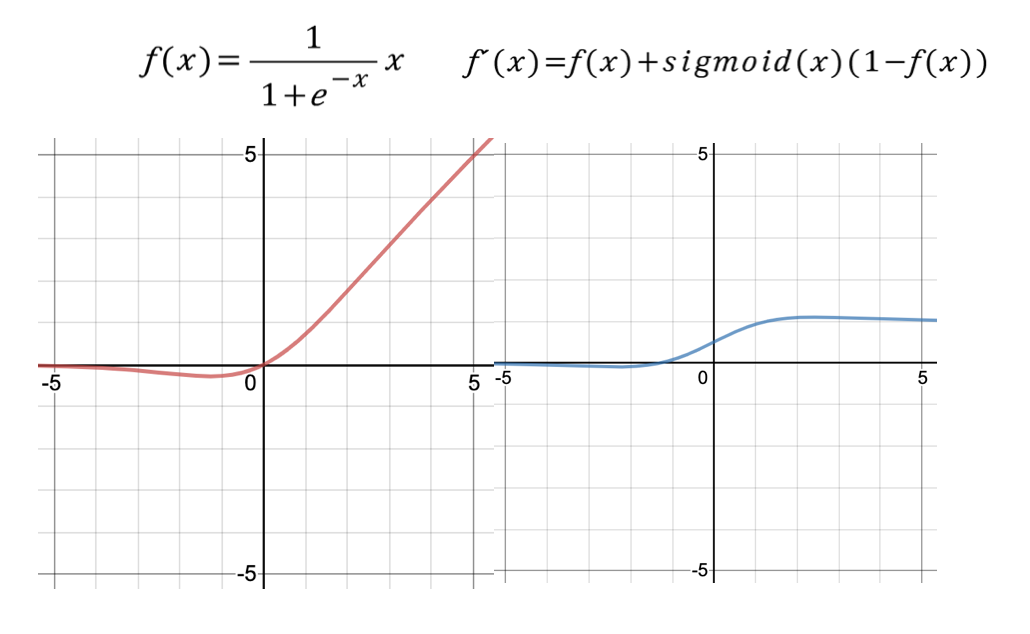1. ReLU
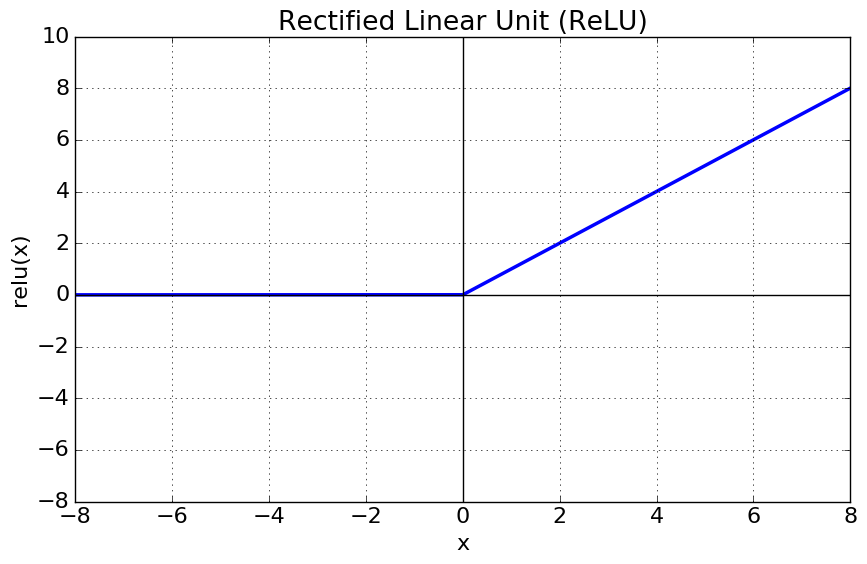
ReLU 함수는 0보다 큰 값을 그대로 출력한다. 매우 간단한 수식을 가지지만, 다음과 같은 특징들을 가지면서 많이 사용된다.
1. 연산 비용이 크지 않고, 구현이 간단하다.
Sigmoid나 tanh 함수는 exp 연산이 필요하지만, ReLU 함수는 비교 연산 하나만 사용되므로 연산 비용이나 구현이 간단하다. 이로 인해 학습이나 추론시에 더 유리하다는 장점이 있다.
2. Gradient Vanishing/Exploding 문제를 유발하지 않는다.
입력 값이 0보다 큰 경우에는 Gradient가 1로 유지되기 때문에, Gradient Vanishing/Exploding 문제를 유발하지 않는다.
ReLU는 위와 같은 강력한 장점을 가지고 있지만, 한편으로 다음과 같은 문제점이 존재한다.
1. 입력 값이 0이하 인 경우에는 Gradient가 0이 되면서 다시 활성화되지 않고 죽는 Dying ReLU 현상이 발생하게 된다.
2. 0이상의 입력값에서는 ReLU 역시 출력값과 미분값이 양수이기때문에 Zig Zag 현상이 발생한다.
2. Leakly ReLU
Dying ReLU 현상을 해결하기 위해 0 이하인 경우에도 값을 가질 수 있도록 설계한 활성화 함수이다. Leakly ReLU 식은 다음과 같다.
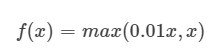
3. PReLU
Leakly ReLU와 거의 유사하지만, 새로운 파라미터를 추가하여 0 이하에서 활성화 함수의 기울기를 학습할 수 있도록 한다.
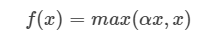
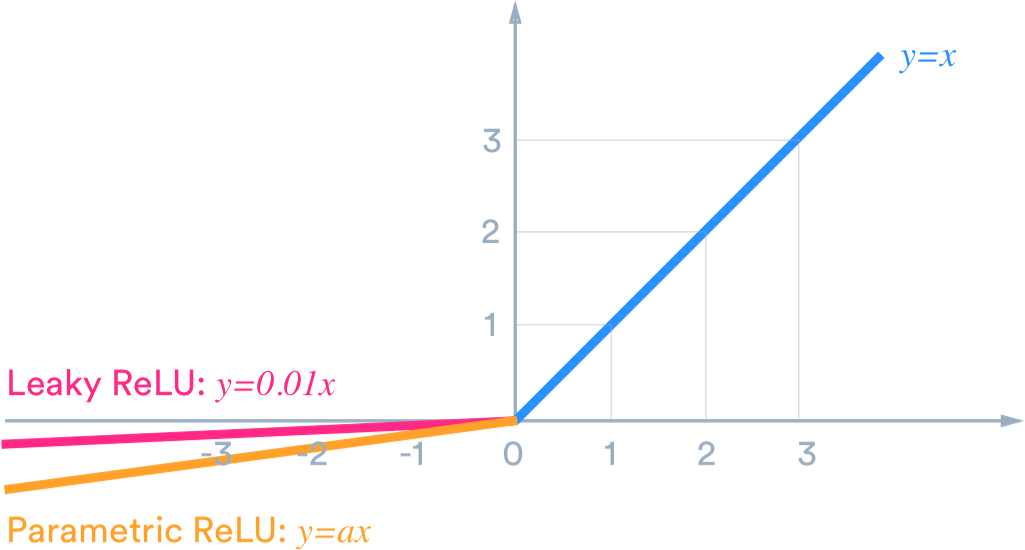
4. ELU
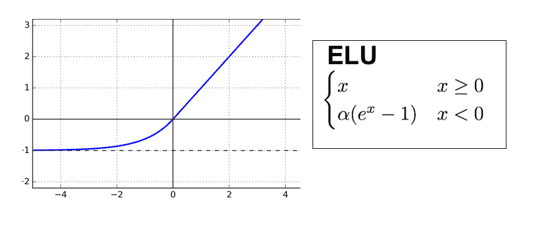
Sharp Point인 0에서 미분이 가능하도록 설계되었고, 0 이하의 입력값들이 -1로 수렴하는 형태의 활성화 함수이다. 출력 값은 거의 Zero-Centered이며, Dying ReLU를 해결할 수 있다.
단, ELU의 경우 exp 연산이 포함되기 때문에 되고 일정 이하의 값에서는 기울기가 0에 수렴하게 되어 Gradient Vanishing 문제가 발생할 수도 있다.
5. Maxout
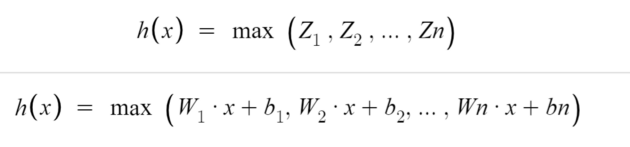
Maxout 함수는 모델에 의해 학습된 활성화 함수이다. 단일 Maxout Unit은 임의의 볼록 함수에 대한 Pixel-wise Linear Approximation(PWL)를 만든다고 볼 수 있다. 위의 수식에서 n은 미리 지정된 값이고, n개의 선형 함수를 통한 임의의 볼록 함수에 대한 근사를 의미한다.
단, Maxout 함수는 최댓값을 선택하는 max 함수를 사용하므로 볼록 함수만을 근사할 수 있다.
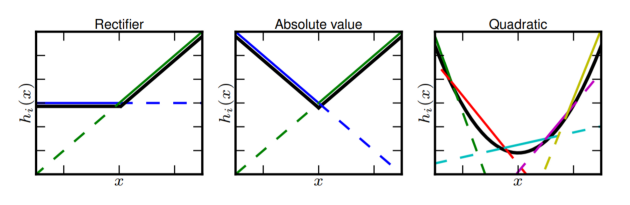
예를 들어 ReLU의 경우에는 max(0,x)와 같이 0과 x라는 선형 함수를 통해 표현할 수 있고, 절대 함수는 max(-x, x)와 같이 -x와 x라는 선형 함수를 통해 표현할 수 있다. 그리고 4개의 선형 함수의 조합을 통해 이차 함수를 근사화 할 수 있다.
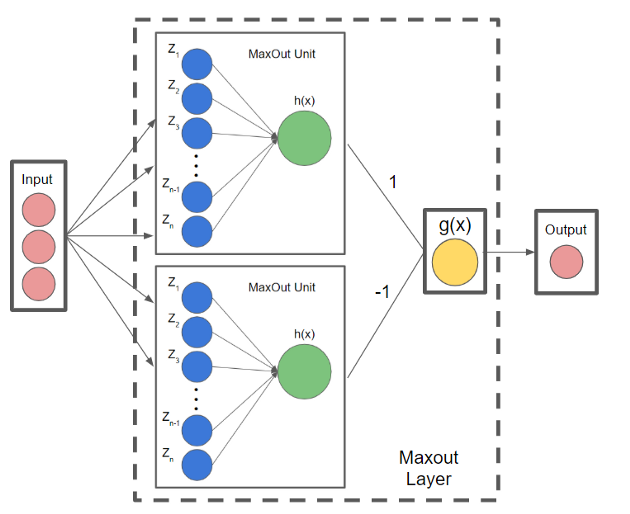
또한, Maxout Unit은 위와 같이 여러개로 구성할 수 있다.
Maxout 함수는 결론적으로 학습을 통해 최적 활성화 함수를 구할 수 있으며, 기존 ReLU이외의 다른 활성화 함수의 문제점을 해결할 수 있다. 한편, 각 Unit 별로 Linear 노드가 많아질수록 최적 활성화 함수의 형태를 표현하여 높은 정확도를 얻을 수 있지만, 노드 수에 비례하여 파라미터 수가 증가하므로 노드를 제한해야 한다.
6. Swish
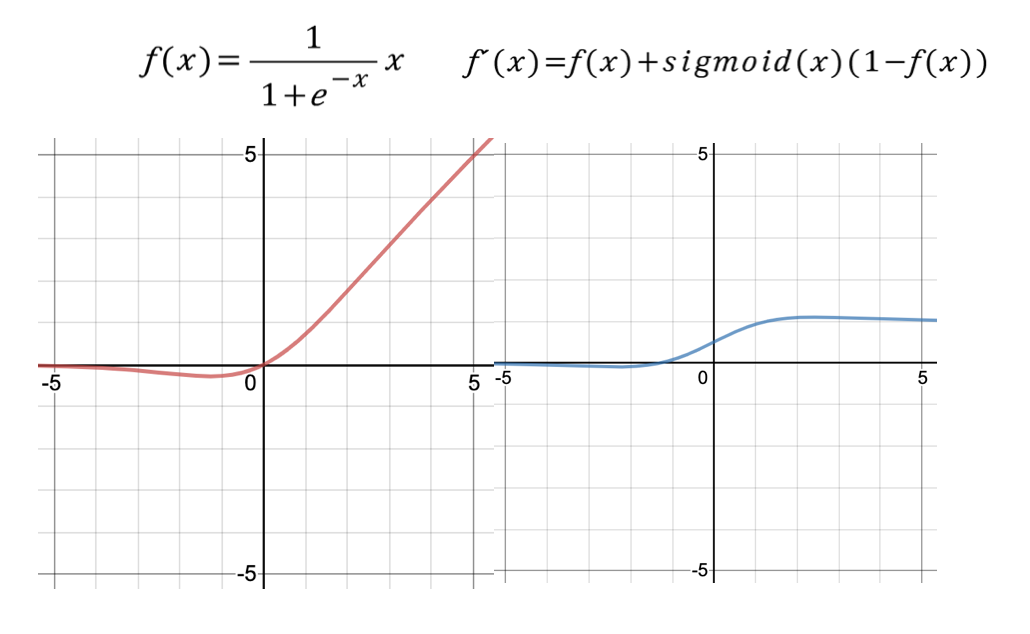
Swish는 ReLU를 대체하기 위해 구글에서 제안한 활성화 함수이다. 식은 위와 같이 Sigmoid 함수에 x를 곱함으로써 ReLU와는 다르게 음수에서도 어느 정도의 값을 가짐으로써 Non monotonicity의 특징을 가진다. 그리고 깊은 레이어를 가진 모델을 학습할 때 ReLU보다 더 좋은 성능을 보인다고 한다.
Vision AI Engineer