SPVNAS(EECV, 2020)

Outdoor Scenes

Outdoor Scenes은 다음과 같은 특징이 있다.
먼저 Light Detection And Ranging(LiDAR) 센서를 이용해서 주로 데이터를 얻는데 아래의 그림과 같이 생겼다. 센서를 통해서 얻어지는 데이터는 찍은 위치에서 멀어질수록 데이터가 희미해지는 특징이 있다. 그리고 찍힌 포인터들이나 공간적 영역이 굉장히 넓다. 그래서 Indoor Scenes에서 사용되던 Point Transformer 혹은 PointNet++와 같은 모델을 바로 적용시키기엔 너무 무겁다.

이러한 특징으로 Voxel을 사용한다. 복셀은 Volume과 Element의 합성어로 굉장히 넓은 영역을 효과적으로 처리하는데 많이 사용되고 있다.
LiDAR Point의 경우, 기본적으로 Sparse & Irregular한 Point Clouds이기에 복셀로 만드는 과정이 필요한데, 그 과정을 Voxelization이라고 한다.
일반적으로 복셀은 정육면체를 사용하여 Sparse & Regular하게 만든다.

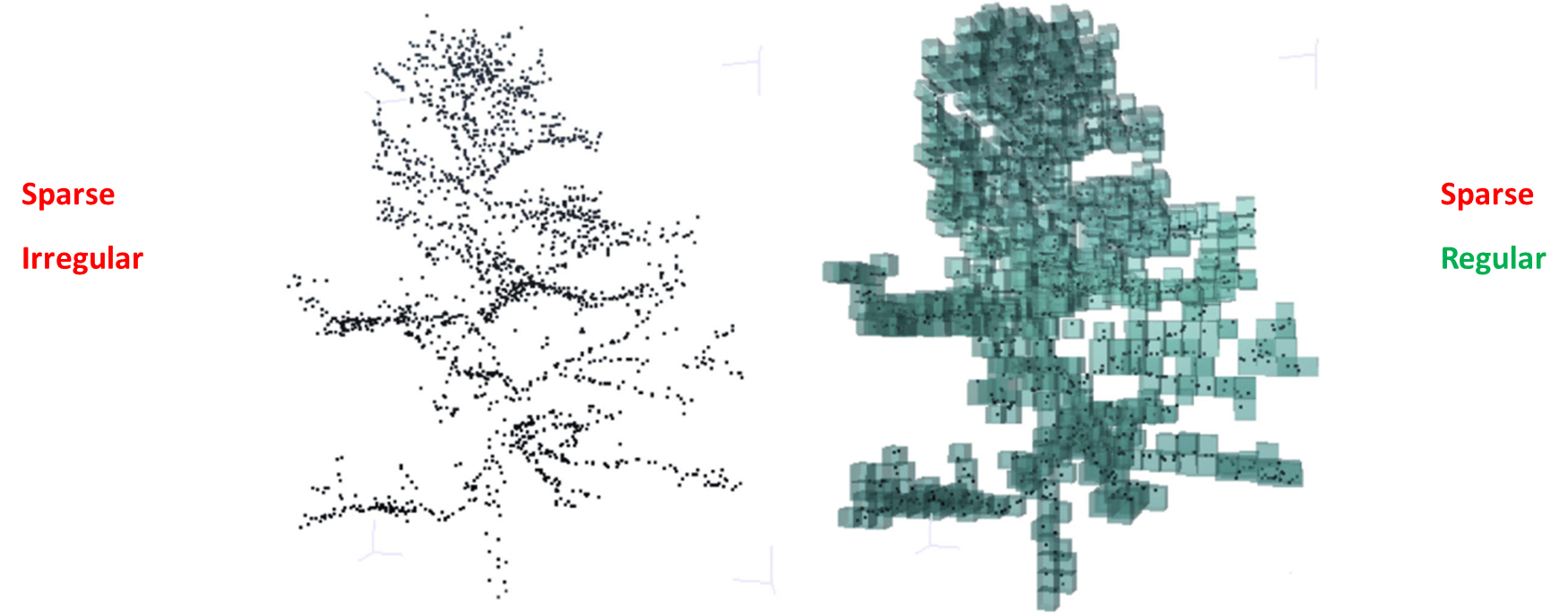
이렇게 Regular하게 만든 복셀 그리드는 Convolution 연산을 쉽게 할 수 있게 된다.
일반적으로 2D처럼 연산을 하게 되면 빈공간이 너무 많아 필요없는 연산이 많아지게 된다. 그래서 제안된 것이 Submanifold Sparse Convolution이다. Output에서 정보가 있는 위치만 찾아서 Convolution 연산을 진행하는 것이다.
그리고 Output이 Input과 동일한 Sparsity가 필요하지 않은데, 그것을 Generalized Sparse Convolution이라고 한다. Output Sparsity를 기준으로 정보가 있는 복셀이 주변에 있는지 찾는 과정이 더해지게 된다.
이 두가지의 차이점은 정적(Static)인지 다이나믹(Dynamic)인지에 달렸다.

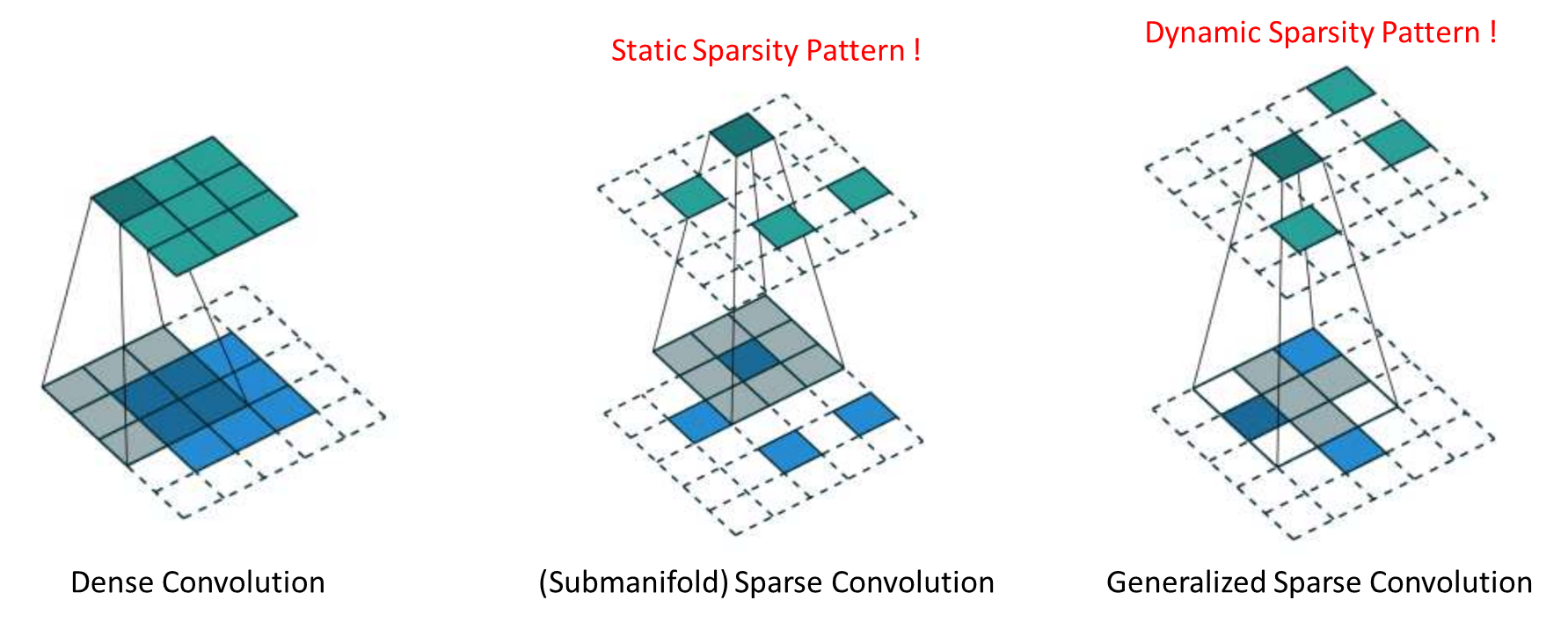
Sparse Convolution

Sparse Convolution 연산이 어떻게 진행되는지 보자.
아래와 같이 Point Clouds가 입력이 되면 PointNet과 같이 xyz 좌표를 sharded MLP를 통해 Symmetric function을 거쳐 Global feature를 만들게 된다면, LiDAR와 같은 경우에는 Point가 굉장이 많은 데이터를 처리하기에 너무 무겁다.

그래서 먼저, Sparse Convolution을 사용하면 아래와 같이, voxelization을 통해서 Sparse voxel grid로 만든다.

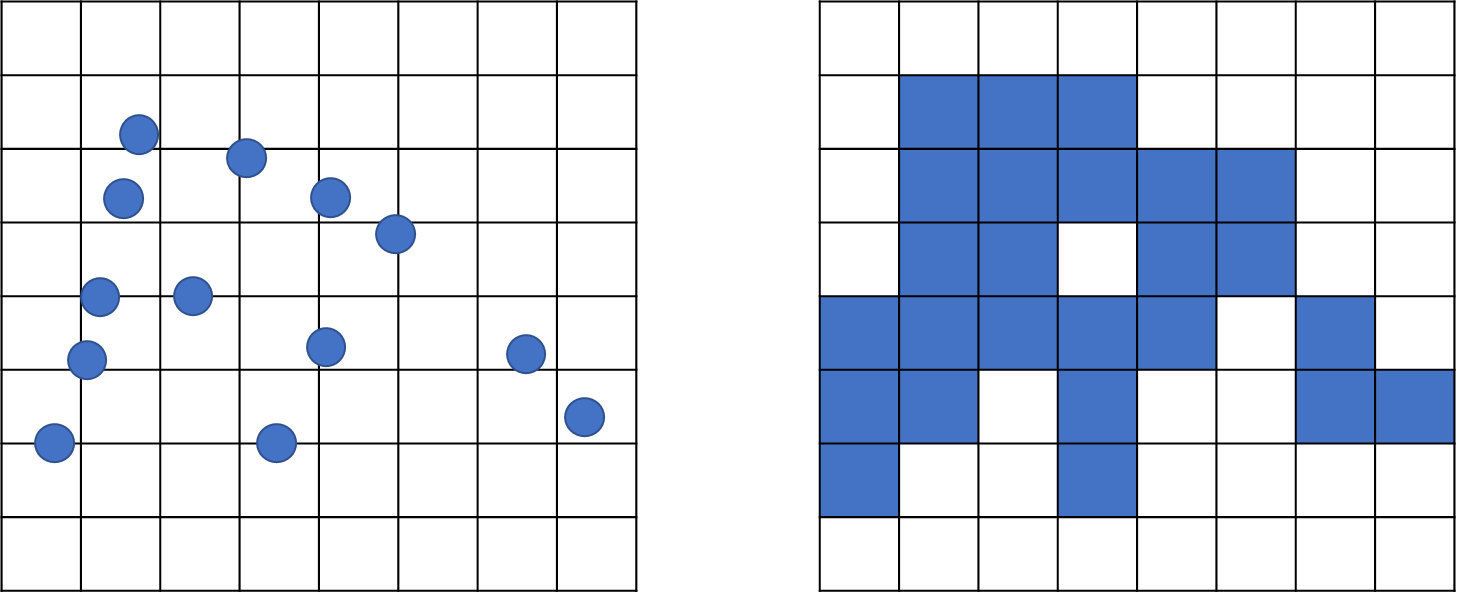
그 다음, 각 복셀에서 주변 point를 찾고 Colvolution을 수행하게 된다.
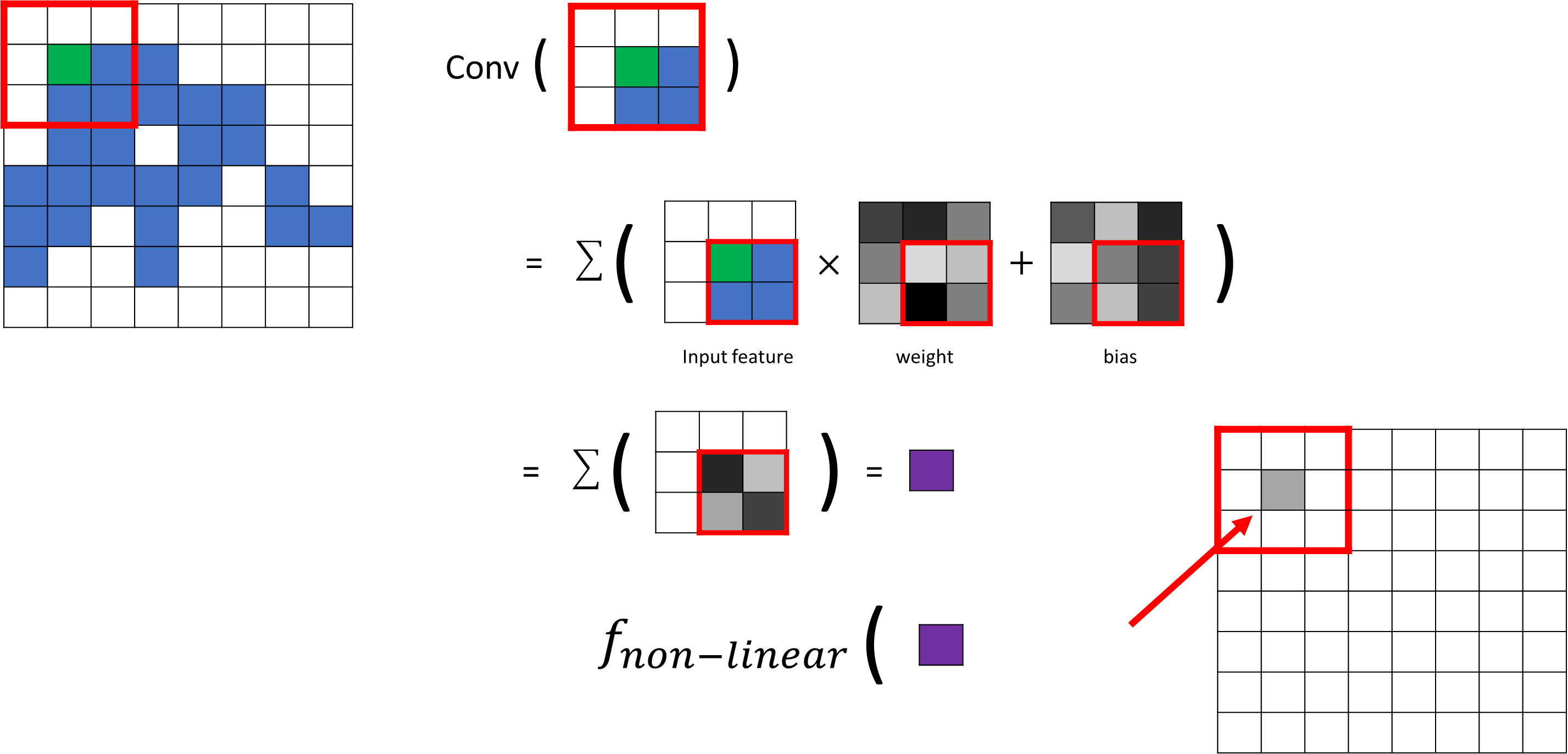
아래의 그림의 초록색 위치에서 데이터가 있는 복셀이 있는지 먼저 찾고, 미리 정의되어 있는 kennel shape에 따라서 각각의 위치에 weights과 bias와 연산이 이루어진다.
기존의 Convolution과는 달리 Sparse Convolution은 데이터가 있는 부분에서만 연산을 수행하게 된다. 그리고 summation을 통해서 Output을 내뱉는다.
그 다음 Output을 활성함수를 통과하게 되면 최종적인 Output feature가 수행되게 된다.

Efficient Neighbor Search with Hash Table

hash table을 사용하여 데이터가 있는 위치를 빠르게 찾는다.
아래의 그림과 같이 Input data가 있다면 Quantized를 하게 되면 인티져 값들로 각각의 위치를 표현할 수 있게 되고, 이 인티져값을 이용하여 Hash table을 만들 수 있다. 인티저는 하나의 Hash key가 되고 그 key에 해당하는 Index를 저장한다.

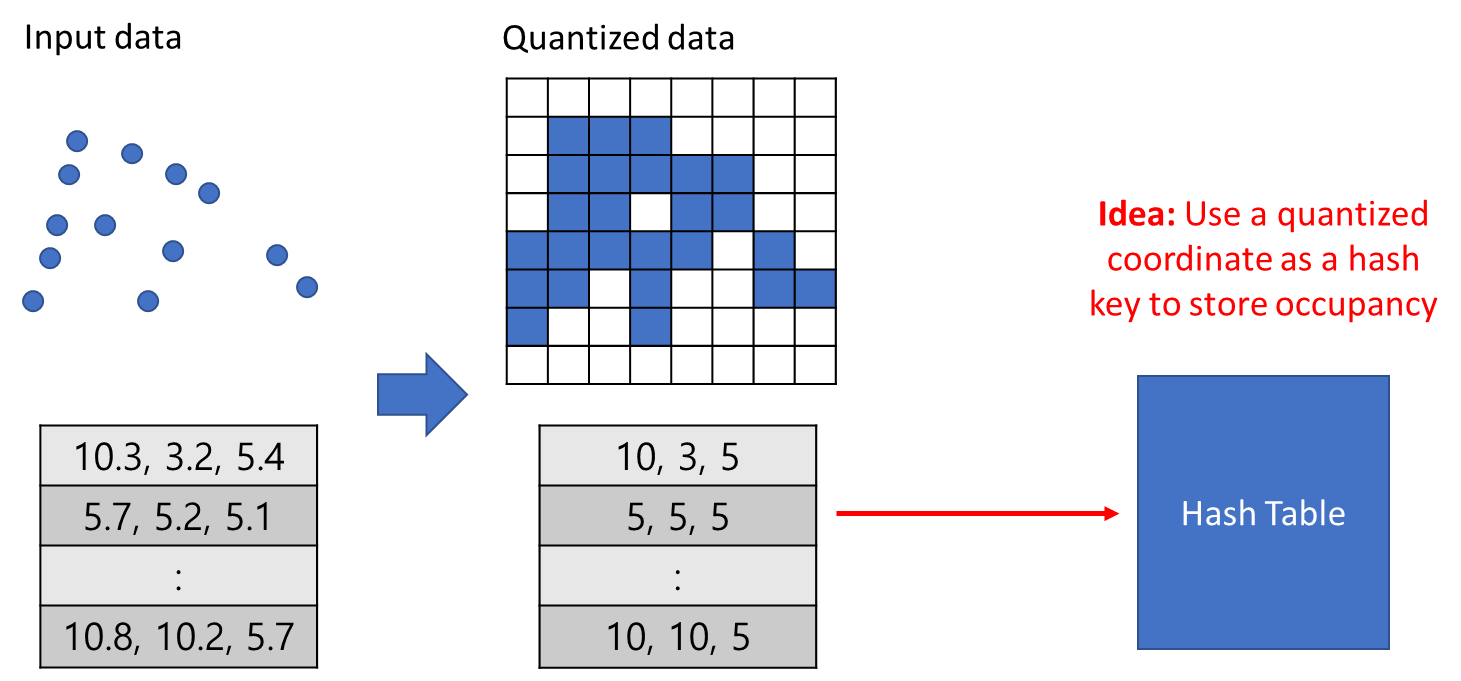
예로 아래와 같이 Quantized data에서 (5, 5, 5)라는 복셀 근처에 존재하는 복셀은 무엇인지 kennel shape에 따라서 후보군 Query를 만들 수 있고 이 Query가 Hash table에 있는지 없는지 확인하여 찾게 된다.

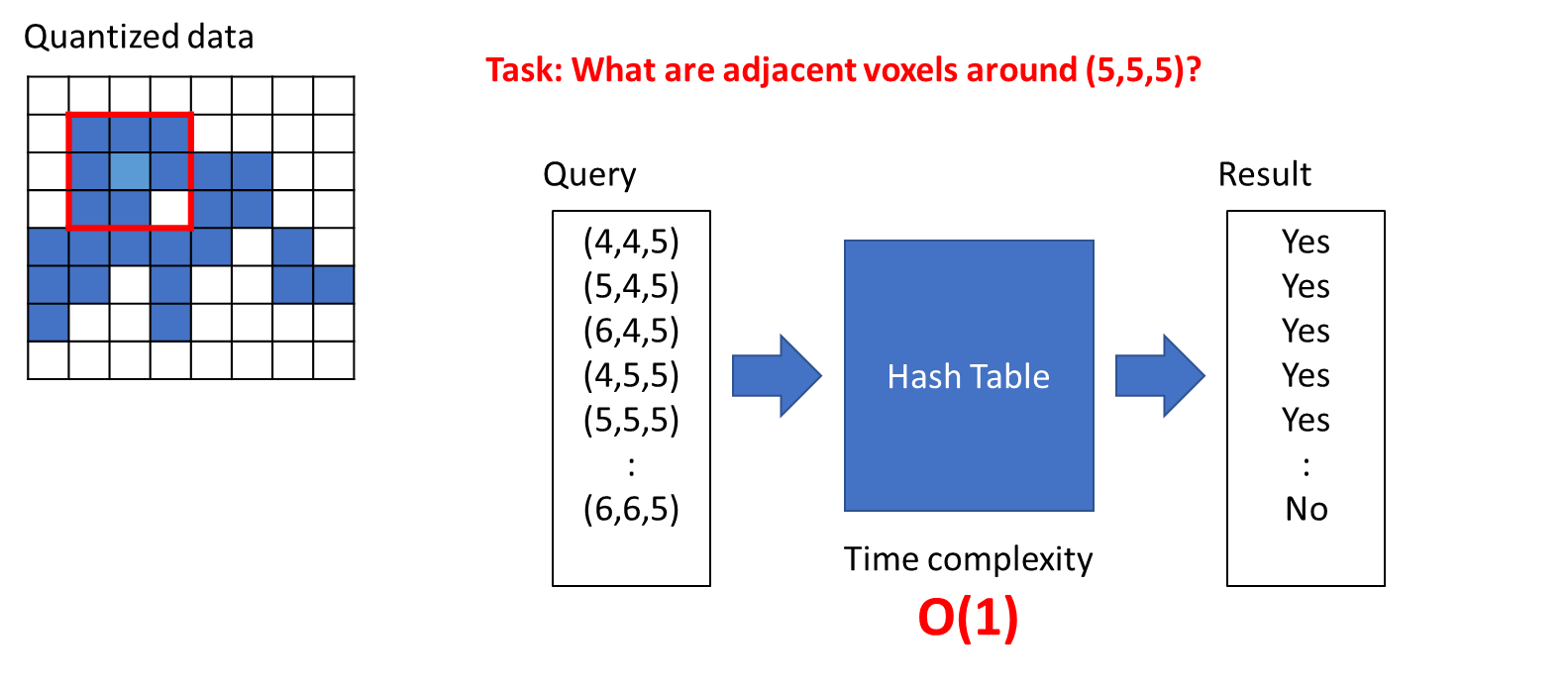
Voxelization을 수행하게 되면 아무래도 detail이 없어지는 단점을 가지지만 수행 속도가 빨라진다는 장점을 가지게 된다. Image로 보자면 고화질에서 저화질로의 변화가 예라고 볼 수 있다. 그래서 정확도 측면에서는 다소 떨어지는 모습을 가지고 있다.
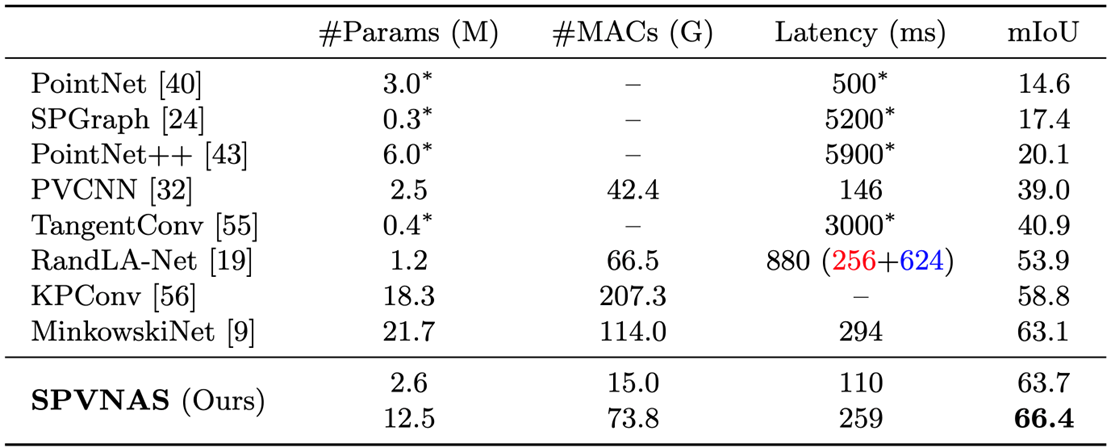
아래의 표에서 그 차이점을 표현하였는데, Point-based와 Voxel-based의 단점을 보완한 새로운 Operation이 바로 SPVNAS다. SPVNAS는 복셀과 Input-point cloud를 모두 사용하는데, 메모리는 사용량은 올라가지만 주변 데이터를 찾을 때 복셀을 이용하기 때문에 빠르게 찾을 수 있고, 정확도 측면에서도 Voxelization을 통해 잃게 되는 위치의 정확도 측면을 Point 기반의 방법으로 보완하여 복셀 기반보다는 좋은 성능을 가지게 된다.

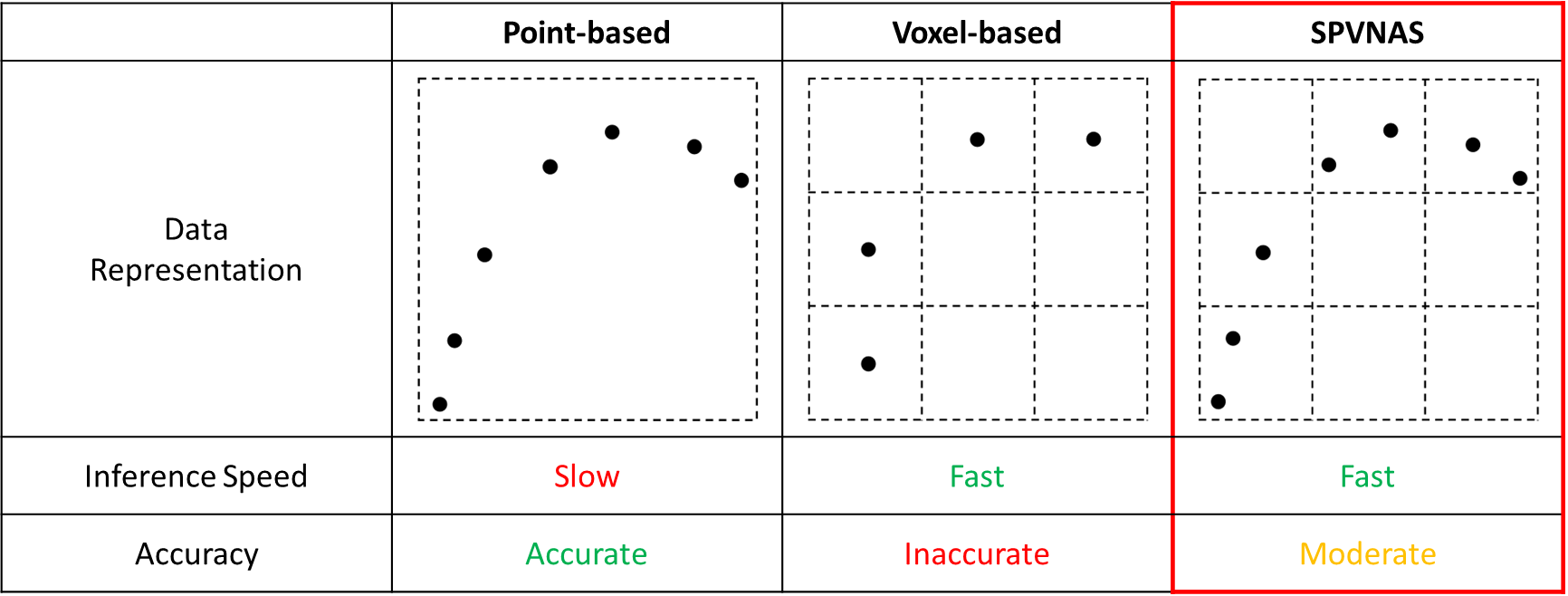
SPVNAS

SPVNAS에서 가장 중요하다고 볼 수 있는 것은 Sparse Point Convoution이라는 새로운 Operation이다.
그리고 여기에서 Efficiency를 조금 증가시키기 위해 NAS를 제안한다.

아래의 그림에서 알 수 있듯이, 형상이 드러나지 않는다는 단점을 가지고 있다. 그래서 classes를 구분하는데 있어서 어려움을 지닌다. 그렇기 때문에 Point Voxel Convolution이라는 제안이 기존에 있었다.

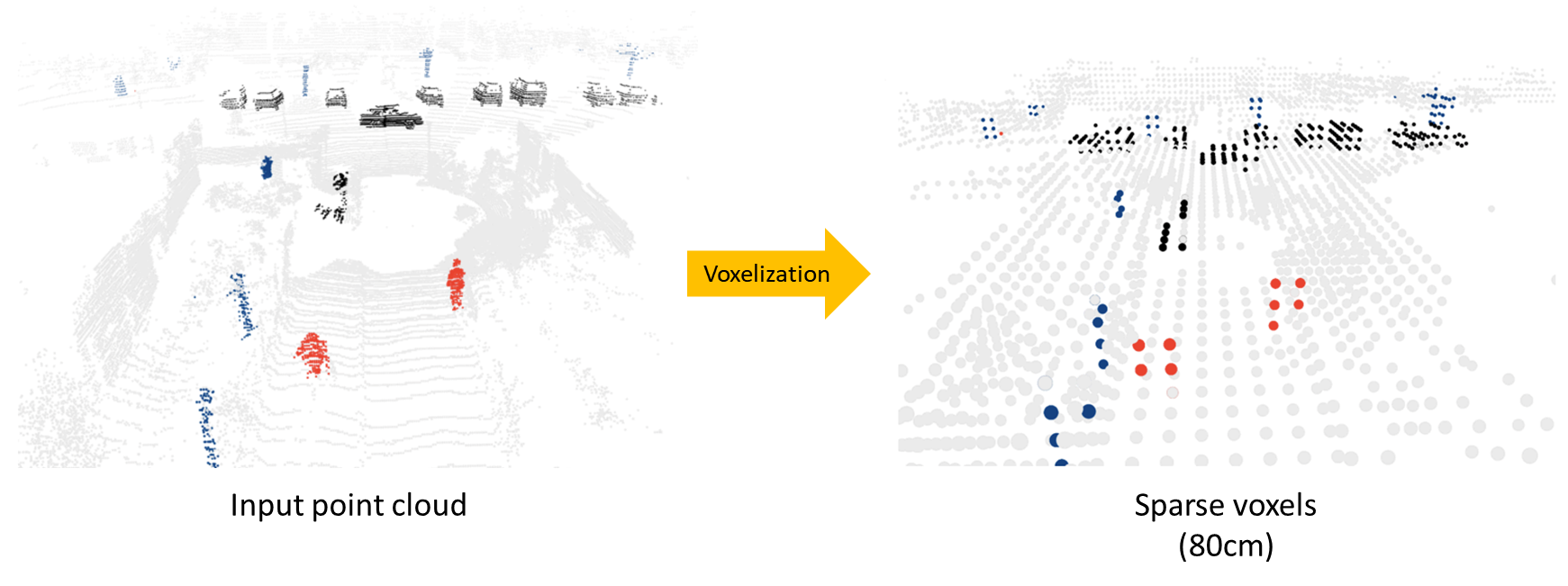
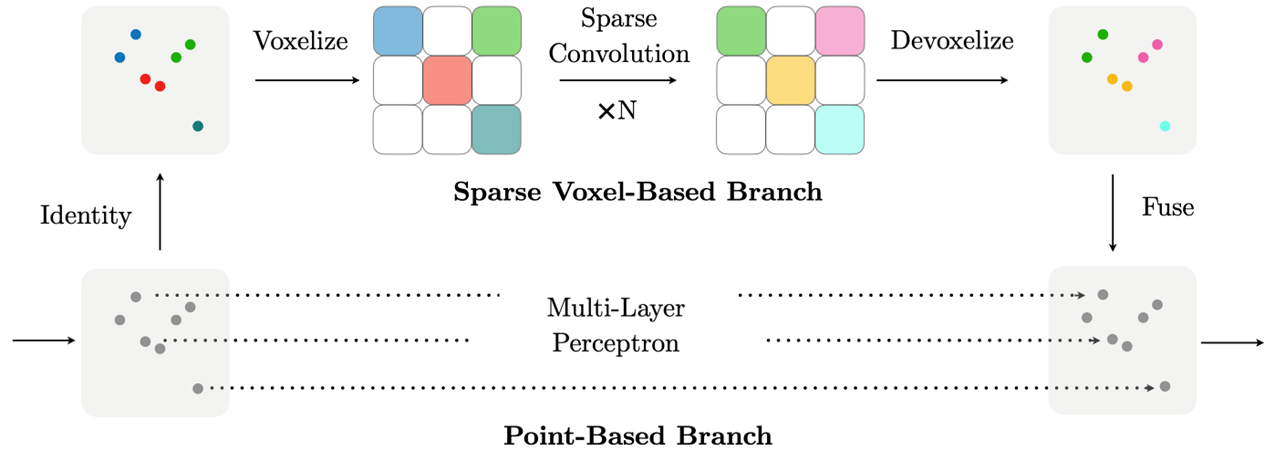
Point Voxel Convolution(PVConv, NeurlPS2019)은 복셀을 사용하기에 효율적이긴 하지만 Dense voxel grid를 사용한다. Dense voxel grid의 경우에는 모든 공간에 데이터가 있다는 전자하에 연산을 하기에 매우 느리다. 이에 반해서 Sparse는 데이터가 있는 공간이 굉장히 적기 때문에 연산이 빠르다.
그럼에도 불구하고 Voxelization을 통해서 연산을 하기에 하나하나의 point의 이웃 데이터를 찾아 연산을 하는 것보다는 빨랐기 때문에 Inference Speed가 빠르다.
순서는 아래와 같은데, MLP과정 이후 Neighbor Search가 없기에 매우 느린 연산 구간은 없다. 그리고 마지막에 voxel feature와 point feature를 합쳐서 최종 Output을 내뱉는다.

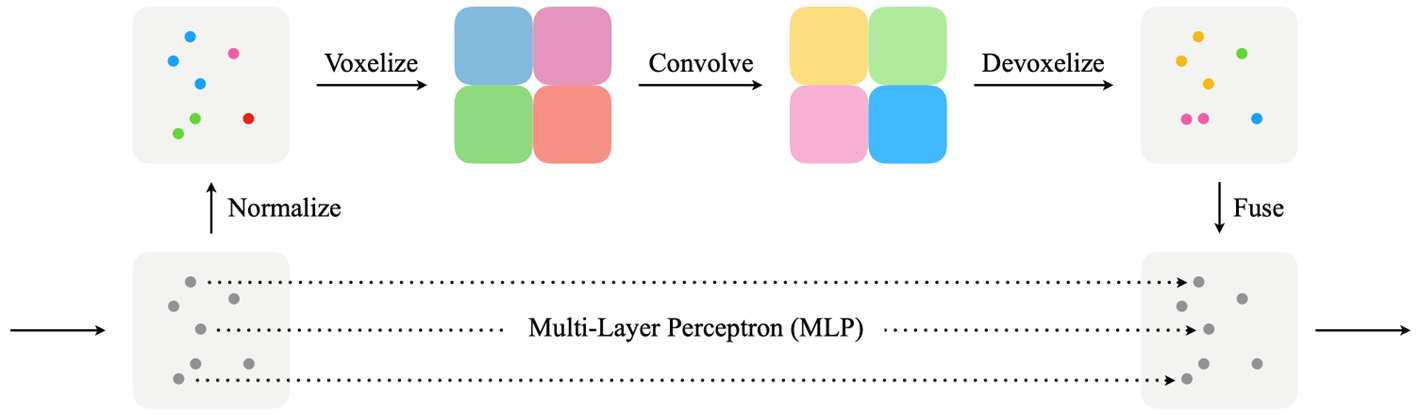
SPVConv는 PVConv에서 Sparse만 추가가 된 버전이다.
그래서 SPVNAS는 Sparse Convolution을 잘 이해하고 적용하는 것이 중요하다고 볼 수 있다.

NAS(Network Architecture Search)

NAS를 간단히 보면, 먼저 사람이 정해놓은 Search Space가 있고 Search Space를 탐색할 Search Strategy를 정한다. 그 후에 Search Strategy 통해서 찾은 아키텍쳐를 찾고 performance를 측정한다. 그리고 performance를 리워드로 사용하거나 이 performance를 기준으로 다른 Search Strategy에서 새로운 아키텍쳐를 찾아내는 방법을 반복한다.

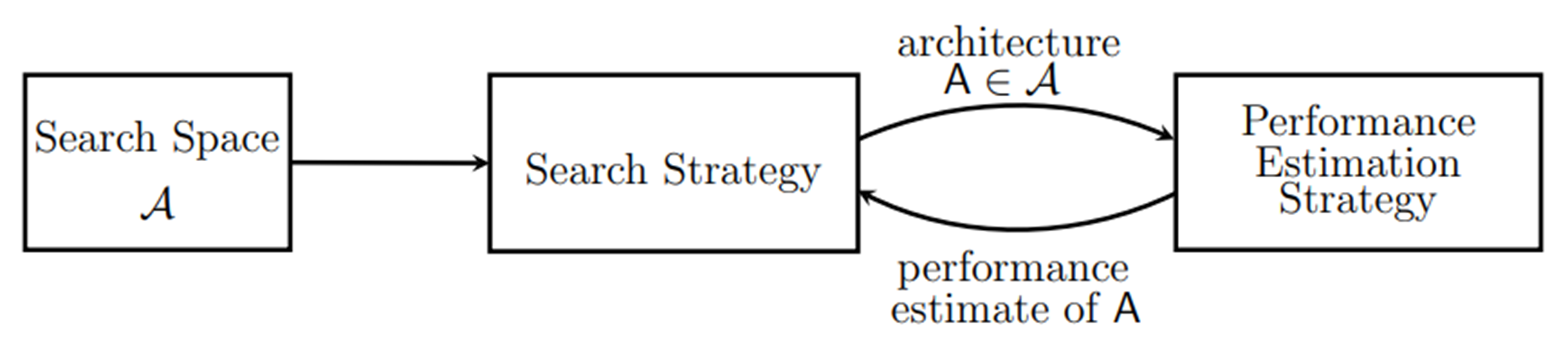
매우 많은 하이퍼 파라미터들을 조정하면서 가장 성능이 좋거나 문제 해결에 맞는 원하는 모델을 찾는 방법이다.

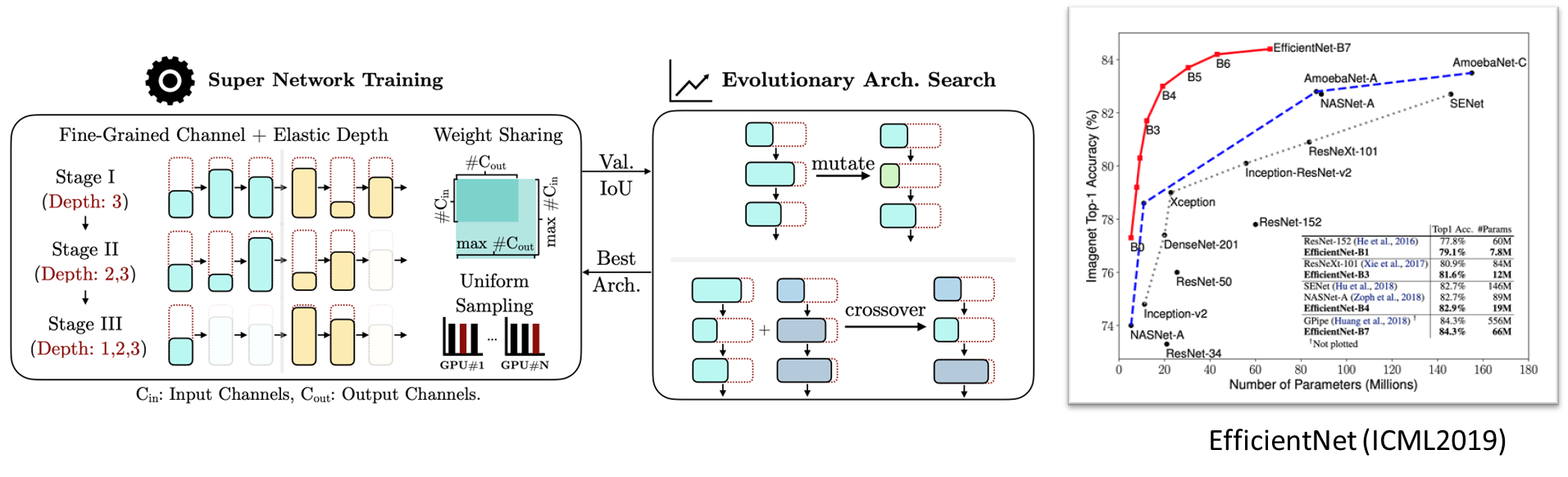
Results

SPVNAS Architecture

SPVNAS Architecture는 torch_scatter와 MinkowskiEngine이라는 모듈을 사용하여 구현을 한다. 그래서 새로운 environment를 생성하여 진행하는 것을 추천한다.

torch_scatter는 Voxelization된 feature를 구하는데 유용하게 사용된다. 버전을 잘 맞춰 모듈을 사용할 수 있도록 한다.
그리고 Sparse Convolution을 제공하는 라이브러리들이 있다. 그 중에서 MinkowskiEngine을 사용하기로 한다.

Coordinate Hashing

Hash table을 구성하는 Hash key를 만드는 과정이다.
복셀이 (N, 3) N개의 3차원으로 입력이 되고, N개의 3차원을 하나의 Hash key를 내뱉는다.

def ravel_hash(voxel_indices):
    # 1. Find the maximum value of each axis.
    max_index = np.max(voxel_indices, axis=0).astype(np.uint64) + 1
    
    # 2. Hashing(xyz에 따른 값을 일렬로 펼치기)
    keys = np.zeros(len(voxel_indices), dtype=np.uint64)
    for d in range(voxel_indices.shape[1] - 1): # dimension
        keys += voxel_indices[:, d]
        keys *= max_index[d + 1]
    keys += voxel_indices[:, -1]
    
    return keys

Voxelization

Voxelization은 voxel size가 입력이 되면 그 입력 공간을 직육면체의 그리드로 나누는 과정이다.
origin은 후에 복원할 때 필요할 수도 있다.

def voxelize(points, voxel_size):
    # 1. Make all the coordinates positive
    origin = np.min(points, axis=0)
    points = points - origin # 양수값으로
    
    # 2. Make the voxel indices and hash keys
    voxel_indices = np.floor(points / voxel_size).astype(np.uint64)
    keys = ravel_hash(voxel_indices)
    
    # 3. Find the unique voxel indices and the mappings.
    _, unique_mapping, inverse_mapping = np.unique(keys, return_index=True, return_inverse=True)
    unique_voxel_indices = voxel_indices[unique_mapping]
    
    return origin, unique_voxel_indices, unique_mapping, inverse_mapping

torch_scatter를 사용하여 voxel features만들기

N = 100
C = 4 # the dimension of point-wise features
l = 1. # voxel size

points = torch.randn(N, 3)
features = torch.randn(N, C)

# First, voxelize the points.
origin, voxels, unique_map, inverse_map = voxelize(points.numpy(), l)
M = len(voxels)
print(f"[voxelization] {N} points -> {M} voxels")

# Then, calculate voxel features.
# Option 1: MaxPool
voxel_features, _ = torch_scatter.scatter_max(features, torch.from_numpy(inverse_map), dim=0, dim_size=M)
print(voxel_features.shape)

# Option 2: AvgPool
voxel_features = torch_scatter.scatter_mean(features, torch.from_numpy(inverse_map), dim=0, dim_size=M)
print(voxel_features.shape)

>
[voxelization] 100 points -> 53 voxels
torch.Size([53, 4])
torch.Size([53, 4])

Sparse Tensor & Convolution

Sparse Tensor는 좌표와 좌표에 해당하는 feature를 하나의 Tensor값을 가지고 있는 sparse voxel grid를 표현한다.
MinkowskiEngine을 사용하여 Sparse Tensor를 생성해 본다.
batch size는 oxel size가 1이기에 하나의 batch size인 0을 가지고, 뒤의 나머지 3개는 points의 xyz와 동일하다.

N1 = 100
C = 4 # the dimension of point-wise features
l = 1. # voxel size

points = torch.randn(N, 3)
features = torch.randn(N, C)

# Make a TensorField (setup for sparse quantization). You can consider this as a point cloud
tfield = ME.TensorField(
    features=features,
    coordinates=ME.utils.batched_coordinates([points / l], dtype=torch.float32)
)
# TensorField -> Sparse Tensor
stensor = tfield.sparse()

print(stensor)
>
SparseTensor(
  coordinates=tensor([[ 0, -3,  0, -1],
        [ 0,  0, -1,  1],
        [ 0,  0, -1, -1],
        [ 0, -2,  0,  2],
        [ 0, -1, -2, -1],
        [ 0,  0,  0, -1],
        [ 0,  0, -1,  0],
        [ 0,  0, -2, -2],
        [ 0,  0, -2,  0],
        [ 0, -1, -1, -2],
        [ 0, -2,  0,  0],
        [ 0,  0,  0,  1],
        [ 0, -1,  0,  0],
        [ 0, -1, -2, -2],
        [ 0, -2, -1, -1],
        [ 0,  0,  0,  2],
        [ 0, -1, -2,  0],
        [ 0, -1,  0, -1],
        [ 0,  0,  0,  0],
        [ 0,  0,  1,  0],
        [ 0, -1, -1,  1],
        [ 0, -2,  0, -1],
        [ 0, -1, -1, -1],
        [ 0,  0, -2, -1],
...
	TensorField [1, 1, 1, ]:	CoordinateFieldMapCPU:100x4
	algorithm=MinkowskiAlgorithm.DEFAULT
  )
  spatial dimension=3)
Output is truncated. View as a scrolla

Sparse Convolution은 2D conv와 비슷한 형태로 되어 있다.
아래의 예를 보자.

# MinkowskiEngine 사용 (input, output, kernel_size, stride, dimension)
sparse_conv = ME.MinkowskiConvolution(C, 2*C, kernel_size=3, stride=1, dimension=3)

out_stensor = sparse_conv(stensor)

print(out_stensor.C.shape) # voxel indices: batch_idx + ijk
print(out_stensor.F.shape) # voxel features: 2*C
print(out_stensor)
>
torch.Size([46, 4])
torch.Size([46, 8])
SparseTensor(
  coordinates=tensor([[ 0, -3,  0, -1],
        [ 0,  0, -1,  1],
        [ 0,  0, -1, -1],
        [ 0, -2,  0,  2],
        [ 0, -1, -2, -1],
        [ 0,  0,  0, -1],
        [ 0,  0, -1,  0],
        [ 0,  0, -2, -2],
        [ 0,  0, -2,  0],
        [ 0, -1, -1, -2],
        [ 0, -2,  0,  0],
        [ 0,  0,  0,  1],
        [ 0, -1,  0,  0],
        [ 0, -1, -2, -2],
        [ 0, -2, -1, -1],
        [ 0,  0,  0,  2],
        [ 0, -1, -2,  0],
        [ 0, -1,  0, -1],
        [ 0,  0,  0,  0],
        [ 0,  0,  1,  0],
        [ 0, -1, -1,  1],
        [ 0, -2,  0, -1],
...
	[1, 1, 1, ]->[1, 1, 1, ]:	cpu_kernel_map: number of unique maps:27, kernel map size:592
	algorithm=MinkowskiAlgorithm.DEFAULT
  )
  spatial dimension=3)

Sparse Point-Voxel Convolution(SPVConv)

위의 함수와 모듈을 사용하여 SPVConv를 구현해본다.

class SPVConv(nn.Module):
    def __init__(self, in_channels, out_channels, kernel_size):
        super(SPVConv, self).__init__()
        self.in_channels = in_channels
        self.out_channels = out_channels
        self.kernel_size = kernel_size
        
        # voxel branch (sparse convolution)
        self.sparse_conv = ME.MinkowskiConvolution(in_channels, out_channels, kernel_size=kernel_size, dimension=3)
        # point branch (shared MLP)
        self.mlp = nn.Sequential(
            ME.MinkowskiLinear(in_channels, out_channels, bias=False),
            ME.MinkowskiBatchNorm(out_channels),
            ME.MinkowskiReLU(True),
            ME.MinkowskiLinear(out_channels, out_channels)
        )
        
    def forward(self, tfield: ME.TensorField):
        # 1. Voxelization
        stensor = tfield.sparse()
        
        # 2. Feed-forward: voxel branch and point branch
        out_stensor = self.sparse_conv(stensor)
        out_tfield = self.mlp(tfield)
        
        # 3. Devoxelize the output sparse tensor to fuse with the output tensor field.
        interp_features, _, interp_map, interp_weights = ME.MinkowskiInterpolationFunction().apply(
            out_stensor.F, out_tfield.C, out_stensor.coordinate_key, out_stensor.coordinate_manager
        )
        
        # 4. Fuse the outputs.
        out = out_tfield.F + interp_features
        
        return out