1) linear model

1-1) equation

선형 모델은 다음과 같이 weighted sum of input features에 constant인 bias term이 더해진 형태를 갖는다.

• $y_{pred}$ : predicted value
• $n$ : feature들의 수
• $x_i$ : $i$번째 feature value
• $\theta_j$ : $j$번째 model parameter
• $\theta_0$는 bias term이며 여기에 곱해지는 $x_0$은 항상 1이다.

위 방정식을 vectorized form으로 나타내면 다음과 같다.

• $\mathbf{\theta}$ : model의 parameter vector
• $\mathbf{x}$ : instance의 feature vector
• $h_{\theta}$ : hypothesis function

머신러닝에서 벡터는 종종 column vector로 나타낸다. 만약 $\mathbf{\theta}$와 $\mathbf{x}$가 column vector라 하면, 두 벡터의 dot product는 prediction $y_{pred}=\theta^T\mathbf{x}$와 같게 된다.

1-2) training a linear model

선형 모델을 학습시킨다는 건 training set에 맞도록 모델의 파라미터를 찾아나가는 것을 의미한다. 그렇다면 모델이 training set에 적합한지 어떻게 판단할까? 이 책에서는 regression model의 성능을 측정할 때 가장 일반적인 방법은 Root Mean Square Error (RMSE)라고 한다. 그러므로 RMSE 값을 구하고, 이 오차값을 최소화하는 $\mathbf{\theta}$를 찾아야 한다.

그런데 RMSE를 구하는 것보다는 이와 같은 결과를 낼 수 있는 Mean Square Error (MSE)를 구하여 최소화하는 계산이 더 간단하므로, 비용함수로 MSE를 이용한다.

선형 회귀 모델을 학습시키는 방법에는 두 가지가 있다. 차례대로 살펴보자.

• a direct "closed-form" equation: training set에 적합한 모델 파라미터를 직접적으로 구하는 방법
  *closed-form equation: 수학적인 해를 단순히 유한한 수의 기본 연산을 통해 구할 수 있는 형태로 표현된 수식
• an iterative optimization approach (Gradient Descent): training set에 대한 비용함수의 크기를 최소화하는 모델 파라미터를 점진적으로 찾아나가는 방법

2) Normal Equation

2-1) normal equation

비용함수를 최소화하는 $\mathbf{\theta}$를 직접적으로 구하는 방법으로, closed-form equation이 있다고 했다. 이를 Normal Equation이라고 한다.

• $\mathbf{\hat{\theta}}$ : 비용함수를 최소화하는 $\mathbf{\theta}$
• $X$ : training set
• $\mathbf{y}$ : 타깃 값을 담은 벡터

선형적인 분포를 가지는 데이터를 임의로 만든 후, normal equation을 이용하여 $\mathbf{\theta}$를 구하고, 이를 이용해 새로운 값을 예측해보자.

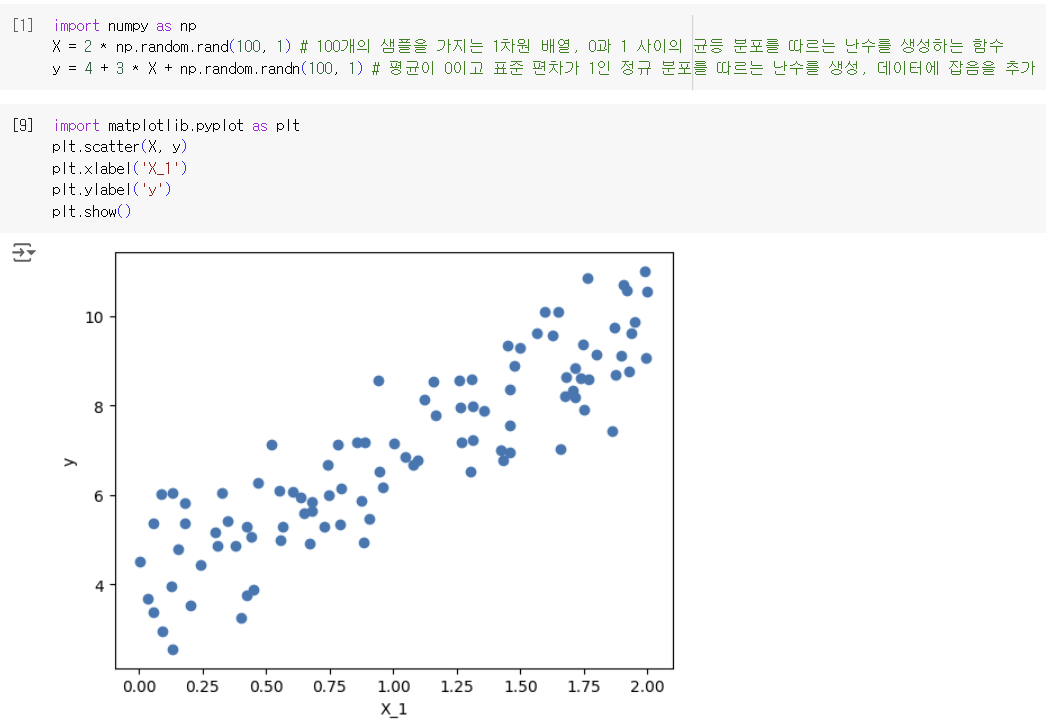
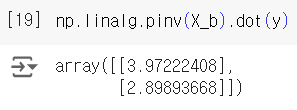
학습 데이터에 절편항을 추가하고, X_b와 y를 normal equation에 넣어 $\mathbf{\theta}$를 구했다. 정답값은 4와 3이지만, gaussian noise 때문에 3.97, 2.89로 나온듯하다.

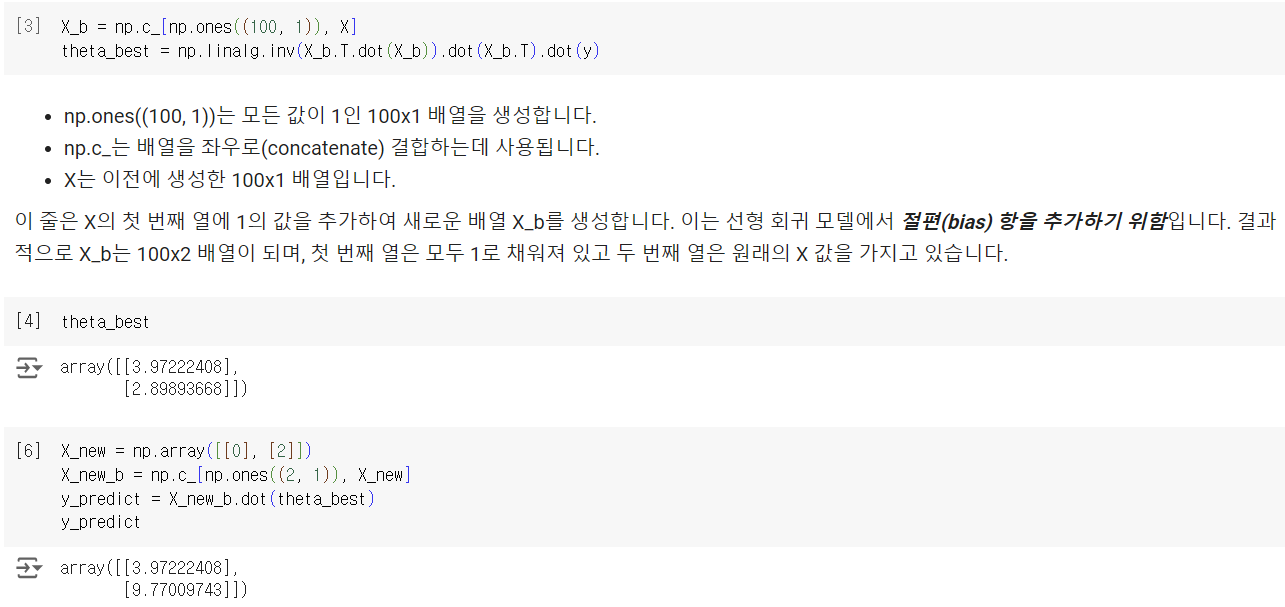
새로운 데이터 포인트를 만들어 $\mathbf{\theta}$를 이용하여 예측값을 구한 뒤 모두 합쳐서 시각화하였다.

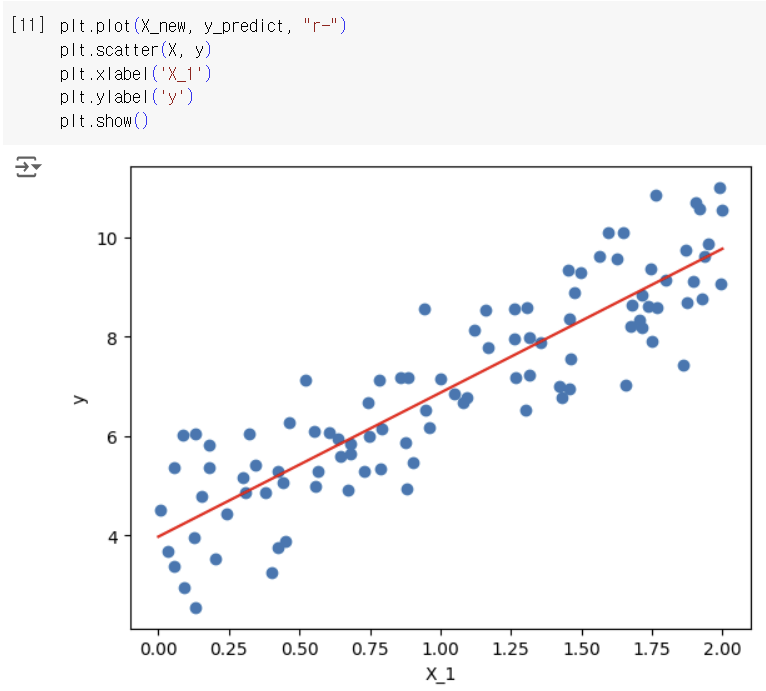
code update!

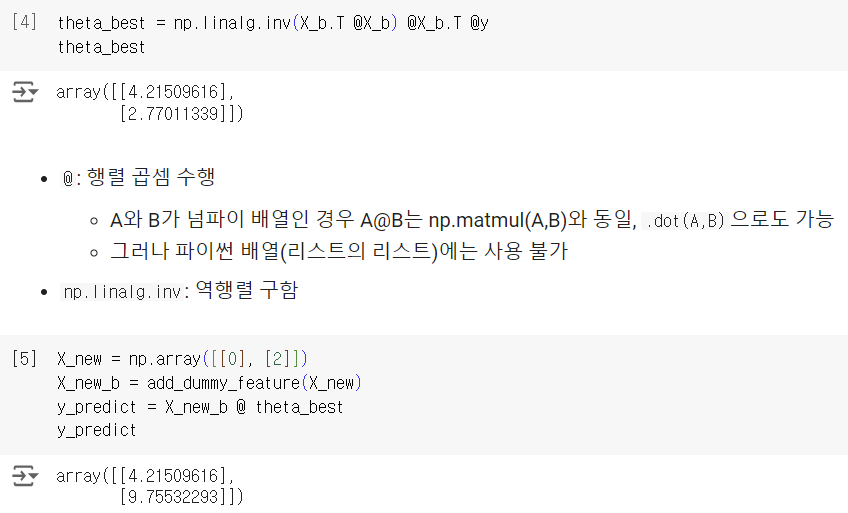
2-2) linear regression using scikit-learn

scikit learn에 있는 LinearRegression 클래스를 이용할 수도 있다. 물론 이 방법은 closed-form equation이 당연히 아니지만, 책에서는 normal equation과 사이킷런의 LinearRegression 함수의 성능을 비교해보고자 넣은 것 같다.

LinearRegression 클래스는 scipy.linalg.lstsq()(손실함수: least squares) 함수를 기반으로 한다. 그러므로 이 함수 역시 오차함수를 최소화하는 best theta $\mathbf{\theta}$를 구할 수 있다. scikit-learn 참고

이 방법은 코드의 길이에서 알 수 있듯 더 간략하며, $X^TX$가 not invertible(=singular)한 경우와 같은 엣지 케이스들을 잘 다룰 수 있다.

normal equation과 다르게 LinearRegression은 $\mathbf{\theta}=X^+ \mathbf{y}$를 계산한다. $X^+$는 $X$의 pseudoinverse이고, 수학적으로는 singular value decomposition(SVD)를 이용하여 계산 가능하고, 코드로는 np.linalg.pinv()를 이용하여 구할 수 있다. pseudoinverse of a matrix 참고

2-3) computational complexity

정규 방정식은 $(n+1)\times(n+1)$ 크기의 $X^TX$의 역행렬을 계산한다. 역행렬을 계산하는 계산 복잡도는 일반적으로 $O(n^{2.4})$~ $O(n^3)$다. 사이킷런의 LinearRegression 클래스가 사용하는 SVD의 계산 복잡도는 약 $O(n^2)$다. 정규 방정식과 SVD는 모두 특성 수(n)가 많아지면 매우 느려지지만, 훈련 세트의 샘플 수에 대해서는 선형적으로 증가한다.(X를 mxn 행렬이라고 할 때, $X^TX$는 $(n\times m)(m\times n)=(n\times n)$ 크기의 행렬이 되므로 샘플 수는 역행렬의 계산 복잡도를 증가시키지는 않고 dot product의 양만 선형적으로 증가시킴. 반면 특성이 2배가 되면 시간 복잡도는 지수적으로 커짐)
*n: 특성 수, m: 샘플 수

정규 방정식이나 다른 알고리즘으로 학습된 선형 회귀 모델의 예측은 매우 빠르다. 예측 계산 복잡도는 샘플 수와 특성 수에 선형적이기 때문이다.

그러나 메모리 공간보다 훨씬 큰 훈련 데이터를 학습하는 경우 시간이 매우 오래걸릴 수 있기에, 더 빠르게 학습시키는 방법으로 "GD"를 소개한다.

3) Gradient Descent

손실함수의 크기를 최소화하는 모델 파라미터를 점진적으로 찾아나가는 방법.

구체적인 내용은 이 블로그를 참고해주세요! ➡️SGD

출처: Hands-On Machine Learning by Aurelien Geron
수정 24.09.30.