Classification Performance Metric

결과에 대한 분석은 매우 중요하다.

Classification 문제에서 모델의 성능 평가에 주로 사용되는 AUC의 개념에 대해 알아보자. 특히 이 개념은 Medical 분야에서 임상 결과나 딥러닝 모델 결과의 성능 평가에서는 빠질 수 없는 개념이므로 잘 알아두도록 하자.

먼저 AUC 값을 구하기 위해서 알아야하는 기본적인 통계 값들에 대해 충분히 이해하고 있어야 한다. 모델의 출력과 decision, 그리고 그 decision의 분류에 대해 알아보고 AUC값이 어떻게 도출되는지, 그것이 어떠한 의미를 갖는지 이해해보자.

ROC-CURVE

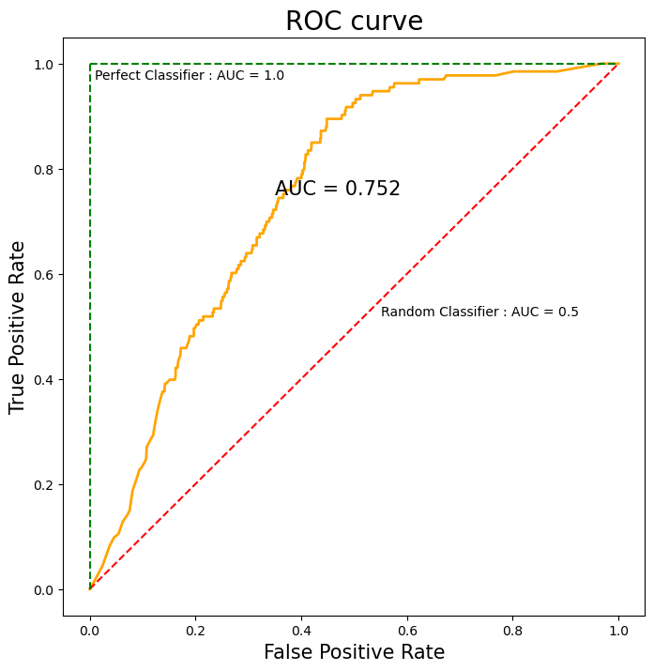
결론부터 이야기하자면 Receiver Operating Characteristic(ROC) curve는 위의 그림과 같이 False Positive Rate를 x축으로, True Positive Rate를 y축으로 하는 그래프이다.

ROC curve는 모든 임계값에 대해 분류 모델의 판단에 대한 결과를 보여주는 그래프인데, 이 임계값은 모델의 판단 기준을 의미하므로 다양한 판단 기준에서 모델의 성능을 전부 표시해놓은 그래프라고 할 수 있다.

이 때, ROC curve의 아래 면적을 Area Under ROC Curve(AUC)라고 한다. AUC가 높다는 것은 모든 임계값에 대해 전체적으로 분류 모델의 성능이 높다는 것을 의미하고, 주어진 task를 아주 잘 수행하고 있다는 것을 의미하고, 이때 그래프는 좌상단으로 치우쳐진다. 반면 분류 모델의 성능이 좋지 않을수록 그래프는 우하단으로 치우쳐지며, $y=x$의 ROC curve는 random classifier와 같다.

이제 대략적으로 이 개념이 무엇을 의미하는지 알았으므로, 이 그래프의 x축(TPR), y축(FPR)이 무엇을 의미하는지, 분류 모델이 각각의 임계값에서 성능이 정해진다는 것이 무슨 의미인지 알아보자.

Confusion Matrix

Confusion Matrix(혼동 행렬)은 모델의 분류 결과를 보여주는 행렬로 하나의 판단 기준(임계값)에서 정해진다. 말 그대로 모델의 혼동 정도를 파악할 수 있으며, 대략적인 모델의 성능을 예측할 수 있다. 혼동 행렬은 아래의 그림과 같이 어떠한 데이터 집단에 대해 실제 값과 예측 값의 분포로 이루어진다. 여기서 말하는 value은 어떤 결과값 자체라기보다는 정해진 임계값에서 모델이 1(positive) 또는 0(negative)으로 판단한 데이터의 갯수를 의미한다. 혼동 행렬로부터 다양한 통계값이 도출된다.

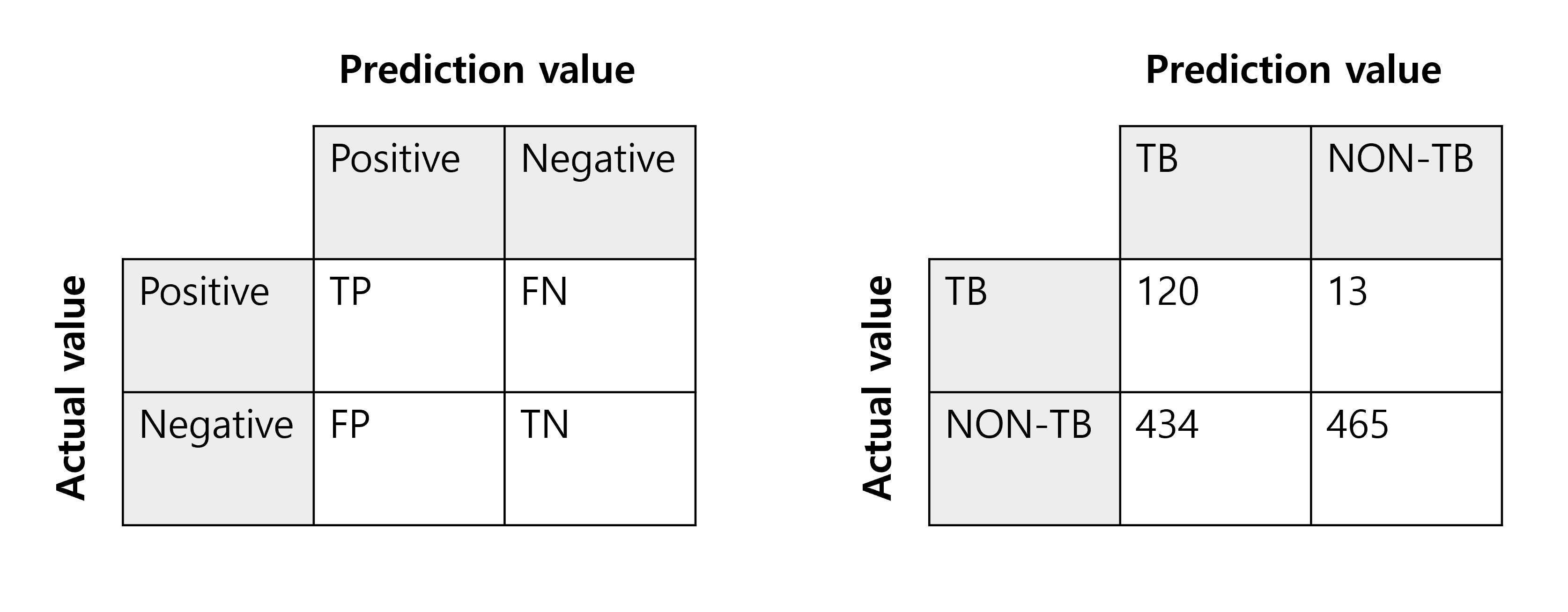
• True Positive(TP) : Positive data를 Positive라고 잘 예측한 케이스
• True Negative(TN) : Negative data를 Negative라고 잘 예측한 케이스
• False Positive(FP) : Negative data를 Positive라고 잘못 예측한 케이스
• False Negative(FN) : Positive data를 Negative라고 잘못 예측한 케이스

TP, TN은 데이터의 실제값을 올바르게 예측한 케이스이고, FP, FN은 데이터의 실제값을 잘못 예측한 케이스이다.

어떤 분류 모델이 병원에 내원한 환자들에 대해 폐 결핵을 가진 환자인지 아닌지 진단하는 경우를 생각해보자. 어떠한 임의의 기준값을 통해 양성 혹은 음성 결과를 정한 진단 결과는 위의 오른쪽 혼동 행렬과 같다. (여기서 실제값(actual value)은 이미 정해져 있는 절대적인 정답(ground truth)이다.)

이 병원에 내원한 환자 1032명 중 실제 결핵균을 가지고 있는 환자는 133명이었고, 결핵균을 가지고 있지 않은 환자는 899명이었다. 모델은 실제 결핵균을 가진 환자 133명 중 120명이 결핵균을 가지고 있을 것이라 예측했고, 13명은 정상 환자일 것이라고 예측했다. 반면 실제 결핵균을 가지고 있지 않은 환자 899명 중 465명을 정상 환자로 잘 구분하였고, 434명을 결핵균이 있을 것이라고 예측하였다.

실제로는 결핵균이 없지만 결핵균이 있는 것으로 예측한 FP가 많다는 것을 알 수 있다.

여기서 파생되는 몇 가지 개념을 알아보자.

• Accuracy(정확도)
  정확도는 주어진 데이터를 얼마나 잘 예측하는지를 나타내는 지표이다. 즉, positive를 positive로, negative를 negative로 잘 예측한 비율을 의미한다.

  $Accuracy = \frac{TP+TN}{TP+TN+FP+FN} = \frac{120+465}{120+465+434+13}=0.567$

• Precision(정밀도)
  정밀도는 모델이 Positive라고 하는 그룹이 있을 때, 이중 실제 positive를 얼마나 잘 예측했는가를 나타내는 지표이다.

  $Precision = \frac{TP}{TP+FP} = \frac{120}{120+434} = 0.217$

• Recall(재현도)
  재현도는 실제값이 positive인 그룹에서 얼마나 모델이 이를 잘 검출해낼 수 있는가를 나타내는 지표이다.

  $Recall = \frac{TP}{TP+FN} = \frac{120}{120+13} =0.902$

• F1 score
  F1 score는 정밀도와 재현율의 조화평균으로 하나의 수치로 나타낸 것으로, 데이터의 positive, negative 비율이 불균형한 상황에서 정확도보다 더 나은 성능 평가를 할 수 있다.

  $F1\;score = \frac{2*Precision*Recall}{Precision+Recall} = 0.350$

Medical statistics

물론 위의 몇 가지 개념도 결과를 잘 해석할 수 있는 중요한 지표이지만, 의학 분야에서는 혼동 행렬을 바탕으로 비슷한 개념을 sensitivity(민감도), specificity(특이도) 등의 개념으로 주로 설명한다.

• Sensitivity(민감도)
  민감도는 실제 질병이 있는 환자군에서 양성으로 잘 예측한 비율이다. 재현율과 구하는 방법이 같고, 이는 관심이 있는 클래스를 얼마나 잘 구별해내는 가에 대한 지표로, 분류 모델의 실용성과 관련이 있다.
  $Sensitivity = \frac{TP}{TP+FN} = \frac{120}{120+13} =0.902$
• Specificity(특이도)
  특이도는 실제 질병이 없는 환자군에서 음성으로 잘 예측한 비율이다. 이는 민감도와 정 반대의 개념이 된다.
  $Specificity = \frac{TN}{TN+FP} = \frac{465}{465+434} =0.517$

• Positive Prediction Value(양성예측도)
  양성예측도는 양성으로 예측된 환자군에서, 실제로 환자가 양성인 비율이다. 정밀도와 구하는 방법이 같다.
  $PPV = \frac{TP}{TP+FP} = \frac{120}{120+434} = 0.217$
• Negative Prediction Value(음성예측도)
  음성예측도는 음성으로 예측된 환자군에서, 실제로 환자가 음성인 비율이다.
  $NPV = \frac{TN}{TN+FN} = \frac{465}{465+13} = 0.973$
• Positive Likelihood ratio(양성우도비)
  양성우도비는 실제로 질병이 있을 때, 예측 결과가 양성인 경우와 실제로 질병이 없을 때, 예측 결과가 양성인 경우의 비율을 의미한다.
  $Positive\;Likelihood\;ratio=\frac{sensitivity}{1-specificity} = \frac{0.902}{1-0.517} = 1.867$
• Negative Likelihood ratio(음성우도비)
  음성우도비는 실제로 질병이 있을 때, 예측 결과가 음성인 경우와 실제로 질병이 없을 때, 예측 결과가 음성인 경우의 비율을 의미한다.
  $Negative\;Likelihood\;ratio=\frac{1-sensitivity}{specificity} = \frac{1 - 0.902}{0.517} = 0.189$
• Prevalance(유병률)
  유병률은 대상 집단에서 질병이 발생하는 비율을 의미하며, 모델의 성능보다는 대상 집단 내에서 해당 질병이 얼마나 드문지를 나타낼 수 있는 지표이다.
  $Prevalance = \frac{TP+FN}{TP+TN+FP+FN} = \frac{120+13}{120+465+434+13} = 0.129$

Decision Threshold

이제 medical field에서 주로 사용되는 분류 모델의 성능 지표에 대해 알아보았으므로, 모델의 예측값과 판단, 그리고 성능에 대해 이해할 수 있다.

지금까지 다룬 모든 성능 지표들은 하나의 판단 기준, 임계점에 대해 정의되는 값이다. 의사가 어떤 환자에 대해 질병이 있는지 없는지 판단을 내릴 때의 자신만의 기준점이 있듯이, 분류 모델도 positive(1)과 negative(0)을 정하기 위해 판단 기준이 있다. 분류 모델은 어떠한 데이터가 주어졌을 때, 이것이 양성일 확률을 출력하고, 이는 0에서 1 사이의 값을 가진다. 이때 주어진 확률값에 대해 이를 positive로 판단을 내릴지, negative로 판단을 내릴지는 threshold의 설정에 달렸다고 할 수 있다. 예를 들어 분류 모델이 하나의 데이터가 positive일 확률을 0.9로 산출하였다 하더라도 threshold가 0.95로 설정되어있다면 이 테스트 데이터는 negative로 판단된다.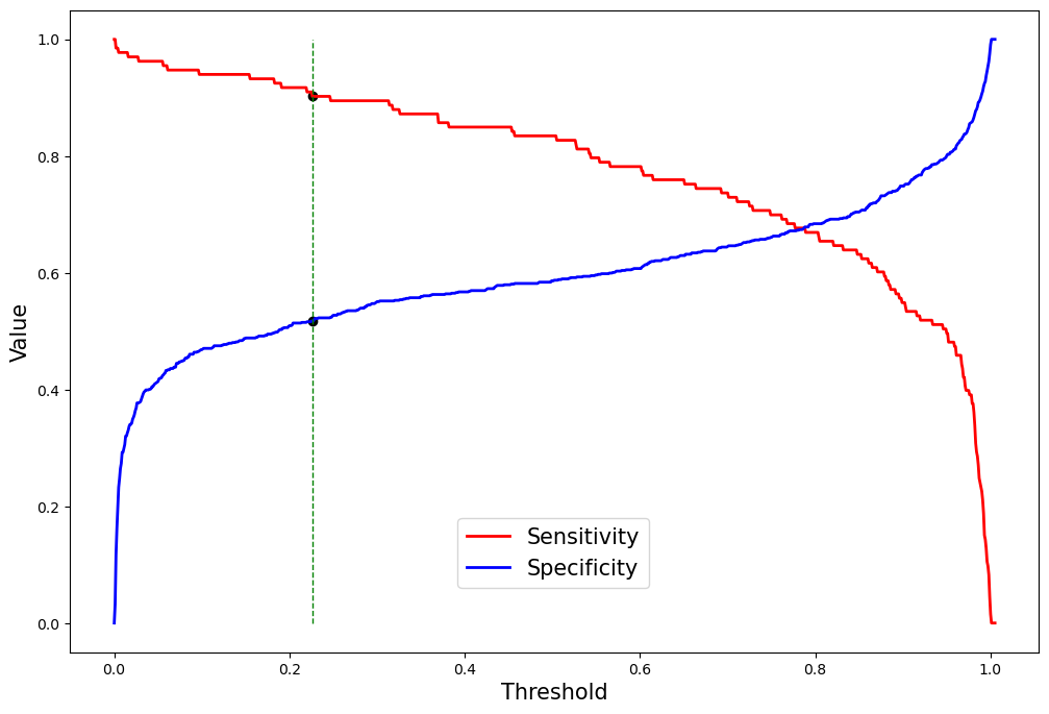

위의 그래프는 결핵 환자에 대한 분류 모델의 판단 기준(threshold)에 따른 sensitivity와 specificity의 변화추이를 나타낸 것이다. 초록색 점선은 현재 설정된 임계점 0.226 (위에서 구한 혼동행렬이 이 판단 기준을 통해 구해진 것)에서 sensitivity(0.902)와 specificity(0.512)를 나타내고, 모든 임계점에 대해 각각의 sensitivity와 specificity를 구할 수 있다.

sensitivity와 specificity는 서로 반비례의 관계에 있기 때문에, sensitivity가 높아지면 specificity가 낮아지고, sensitivity가 낮아지면 specificity가 높아진다.

그러므로 사용자가 원하는 조건에 맞게 적당한 threshold를 선정하여 분류모델을 활용하는 것은 매우 중요한 작업이다. WHO(World Health Organization)에서 요구하는 결핵 분류 CAD(Computer Aided Detection) 모델의 성능은 sensitivity 0.9 기준 specificity 0.7이다. 위의 그래프 또한 sensitivity 0.9일 때의 threshold에 맞춰진 상태이고, 이 때 specificity는 0.512였다. 아직 한참 부족한 모델이다..

AUC

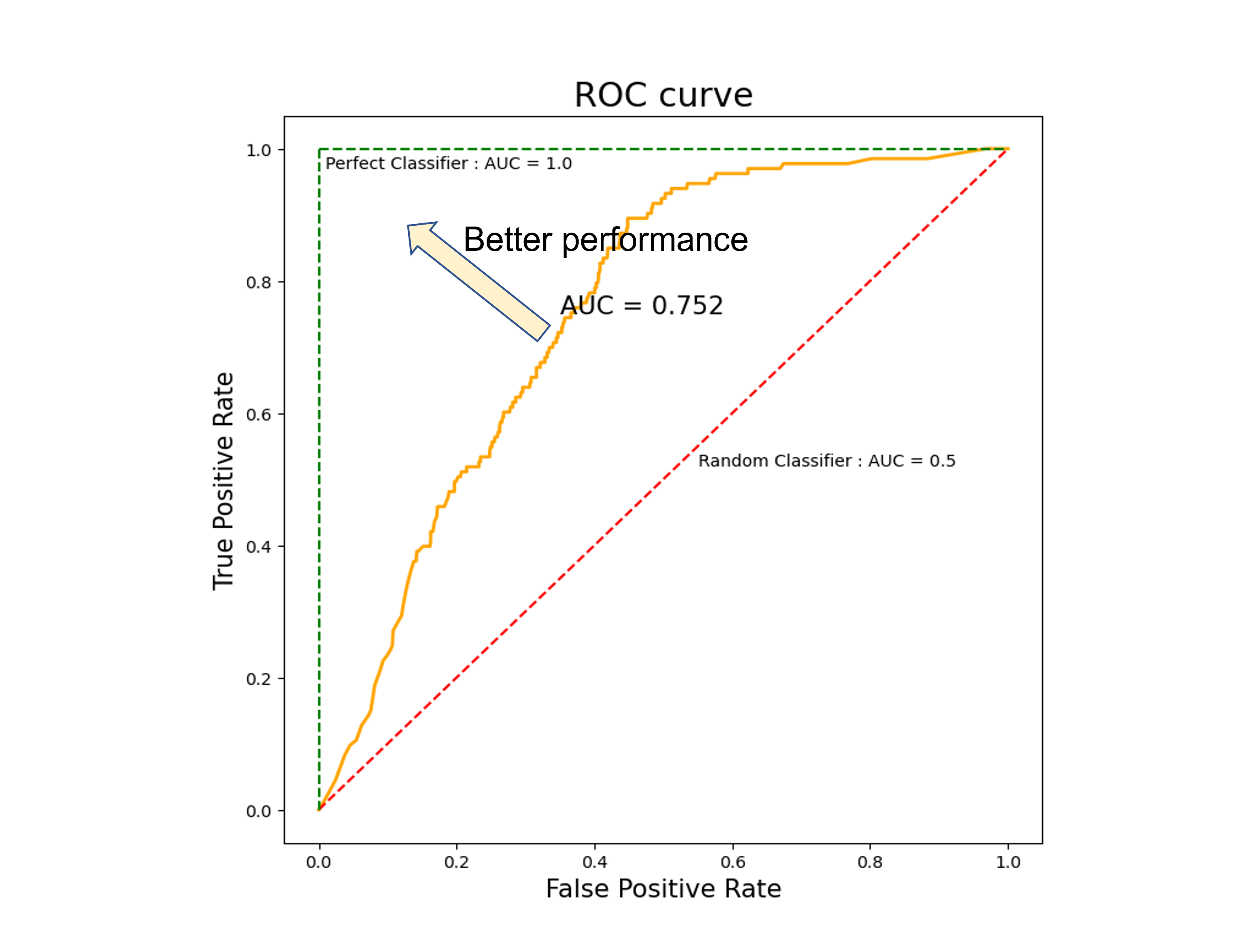
다시 ROC-Curve로 돌아와서, x축(TPR)과 y축(FPR)를 살펴보자.

• True Positive Rate(TPR)
  실제 질병이 있는 환자군에서 양성으로 잘 예측한 비율로, 민감도(sensitivity)와 같은 개념이다.
• False Positive Rate(FPR)
  실제 질병이 없는 환자군에서 양성으로 잘못 예측한 비율로, 1-특이도(specificity)와 같은 개념이다.

TPR은 높을수록 좋은 수치이고, FPR은 낮을수록 좋은 수치라고 할 수 있다.

Sensitivity와 specificity는 반비례 관계에 있다고 하였으므로, TPR(sensitivity)와 FPR(1-specificity)는 비례 관계에 있다. 예를 들어, 분류 모델이 모든 환자를 결핵이라고 판단한다고 하자. (threshold = 0) 이때, sensitivity는 1, specificity는 0이고, TPR = 1, FPR = 1이 될 것이다. 반면에 분류 모델이 모든 환자를 정상으로 판단한다고 하면, (threshold = 1) sensitivity는 0, specificity는 1이고, TPR = 0, FPR = 0이다.

즉, threshold가 0에서 1로 바뀌어가면서 모든 threshold에서 TPR과 FPR를 구해 plot하면, ROC curve는 (1,1)에서 (0,0)를 잇는 그래프가 된다.

모델의 성능을 판단할 때, 우리는 sensitivity와 specificity가 둘 다 높기를 바란다.

위에서 언급했듯이 이 두 값은 반비례 관계에 있으므로, FPR(1-specificity)가 낮을 때, TPR(sensitivity)가 높다는 것이 sensitivity와 specificity가 둘 다 높다는 것을 의미한다. threshold가 0에서 점점 높아질수록 positive로 예측되는 데이터의 갯수가 적어지므로, TPR과 FPR은 동시에 작아질 수 밖에 없다. 하지만 FPR가 줄어드는 정도보다, TPR가 줄어드는 정도가 더 작다면 FPR가 작은 경우에도 TPR가 높을 수 있을 것이다. 그리고 그것은 ROC curve가 좌상단으로 많이 치우쳐질수록 좋은 분류 성능을 갖는 모델이라는 것을 의미한다.

AUC는 ROC curve 아래 면적을 의미한다. ROC curve가 좌상단으로 치우쳐질수록 분류 성능이 좋은 모델이므로, 그래프 아래 면적이 클수록 분류 성능이 좋은 모델이라는 것을 의미한다. 정리하자면 AUC는 분류 모델의 모든 판단 기준(threshold)에서 specificity와 sensitivity 관점에서 전체적인 성능을 수치화 한것으로 생각할 수 있다. 모든 threshold에서 대상군을 완벽하게 분류해낼 수 있다면 ROC curve는 초록색 점선과 같은 그래프가 될 것이므로 분류 모델이 가질 수 있는 최대의 AUC는 그 때 아래 면적인 1이 될 것이다. 반면에 분류 모델이 무작위로 결과를 내도록 만들어졌다면 FPR이 감소함에 따라 TPR이 즉각적으로 감소하는, (1,1)과 (0,0)을 잇는 직선이 될 것이고, 이 때 AUC는 0.5가 된다.

Discussion

또 다른 관점으로는 AUC를 positive example의 probability의 distibution이 negative example의 probability distribution보다 높은 정도를 수치화한것으로도 생각할 수 있다. 이진 분류에서 positive example의 output probability가 negative보다 더 높게 나와야 좋다는 것은 아주 당연한 이야기긴 하다.

완벽한 분류기에서는 모든 positive example의 output probability가 모든 negative example의 probability보다 높다. 반면 random 분류기에서는 두 probability distribution이 완전히 겹쳐있게 된다.

그러므로 CNN을 기반으로 추출한 feature vector를 이용해 분류하는 모델의 경우, AUC는 추출한 feature의 clustering 정도를 의미할수도 있다.