Convolutional Neural Network

신희준·2022년 10월 29일

Background Knowledge

목록 보기

6/12

Computer vision에서 Deep learning을 사용할 때, 필수적으로 알아야하는 CNN에 대해서 알아보자.

1. Convolution

(1) LTI system

시스템은 어떤 input에 대해 response하여 동작하는 장치이다. 여기서 반응을 output으로 생각하면 된다. 신호처리에서는 시스템을 filter 혹은 kernel이라고 볼 수 있다. (쉬운 이해를 위해 discrete signal 가정)

y(n) = F(x(n))

n은 time step을 나타낼 수도, 공간 상의 좌표를 나타낼 수도 있다.

LTI system은 이 시스템이 아래의 두 가지 특성을 가질 때를 의미한다.

Linear system : superposition & scaling 만족
$y_1(n) = F(x_1(n)), \; y_2(n) = F(x_2(n))$ $F(a_1x_1(n)+a_2x_2(n)) = a_1F(x_1(n)) + a_2F(x_2(n)) = a_1y_1(n) + a_2y_2(n)$
Time-Invariant system
$y(n) = F(x(n))$ $y(n-n_0)=F(x(n-n_0))$

우리는 이 system을 구하고자 하는데, 이때 꼭 필요한 개념이 impulse signal이다.

Impulse signal은 $n=0$ 일 때만 크기가 1이고, 나머지에선 크기가 0인 신호이다.

\delta[n] = \begin{cases} 1,\;if\;n=0\\ 0,\;if\;x\ne0 \end{cases}

Impulse function은 sifting property를 가지고 있어서 특정 값을 골라낼 수가 있다.

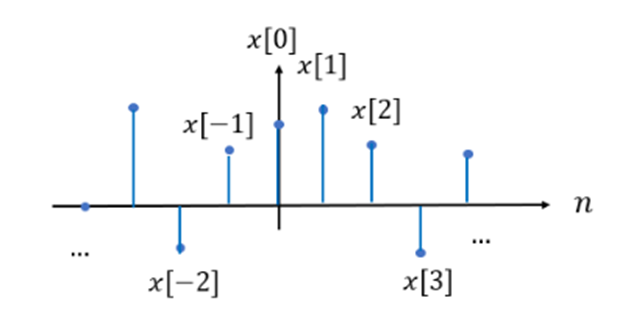
예를 들어, 위와 같은 discrete time signal $x(n)$ 에서, $x(2)$ 신호만을 추출하고자 하면 $x(2)\delta(n-2)$ 를 사용할 수 있다.

즉, $x(n)$ 을 모두 표현하고자 한다면 아래와 같이 할 수 있다.

x(n) = ... + x(-2)\delta(n+2) + x(-1)\delta(n+1) + x(0)\delta(n) + ...

=\sum_{k=-\infty}^{\infty}x(k)\delta(n-k)

어떠한 DT singal도 shifted $\delta(n)$ 의 합으로 표현될 수 있다.

이제 아래와 같은 LTI system이 있다고 해보자.

y(n)=H\{x(n)\} = H\{\sum_{k=-\infty}^{\infty}x(k)\delta(n-k)\}

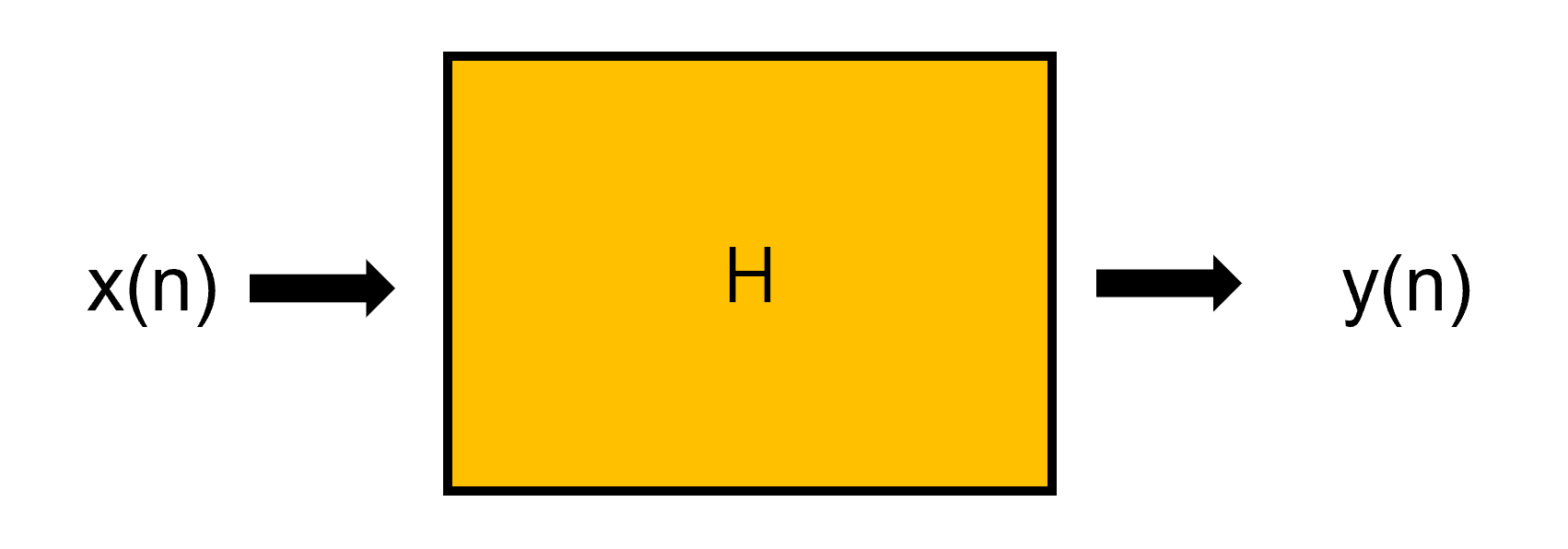
H가 linear하다면 superposition과 scaling이 가능하므로,

y(n)=H\{x(n)\} = \sum_{k=-\infty}^{\infty}H\{x(k)\delta(n-k)\} \quad \because superposition

y(n)=H\{x(n)\} = \sum_{k=-\infty}^{\infty}x(k)H\{\delta(n-k)\} = \sum_{k=-\infty}^{\infty}x(k)h_k(n) \quad \because scaling

여기서 $h_k(n)$ 은 impulse response function으로, unit impulse function이 LTI system의 input으로 들어갔을 때의 출력 값을 의미한다. $h_k(n) = h(n-k)$

결론적으로 LTI system은 다음과 같이 쓸 수 있다.

\underset{output\;signal}{\underline{y(n)}} = \sum_{k=-\infty}^{\infty}\underset{input\; signal}{\underline{x(k)}}\cdot\underset{impulse\;response}{\underline{h_k(n)}}

y(n) \overset{def}{=} x(n) * h(n) \quad \gets convolution

여기서 convolution의 정의가 나온다. LTI 시스템에서는, 임펄스 반응이 그 시스템을 완벽히 설명할 수 있으며, LTI 시스템의 출력은 시스템의 임펄스 반응과 입력의 convolution이다. 즉, convolution은 LTI 시스템에서 입력과 출력 사이의 mapping을 의미한다.

LTI system은 곧 filter라고 했으므로, LTI system의 impulse response는 시스템 그 자체로, 필터를 설계한다는 것은 impulse response $h(n)$ 을 결정하는 것이다. Impulse response는 그러므로 어떤 입력에 대해 원하는 출력이 나오도록 설계가 되어야 한다.

(2) Convolution의 특성

출처 : https://en.wikipedia.org/wiki/Convolution

이제 convolution 연산의 특성에 대해 더 알아보자. 위에서 알아본 convolution을 continuous signal에 대해서 표현하려면 합에서 적분으로 바뀌면 된다. 임의의 $f$ signal과 $g$ signal의 합성곱은 다음과 같이 쓸 수 있다.

(f*g)(t)=\int_{-\infty}^{\infty}f(\tau)g(t-\tau)d\tau

이는 하나의 함수 $g$ 를 $y$ 축 대칭 이동 시키고, $t$ 만큼 대칭이동 시킨 함수와 $f$ 함수와 곱한 결과를 $f$ 의 모든 x값에 대해 전부 다 적분한 것을 의미한다.

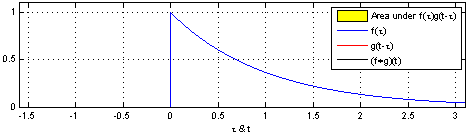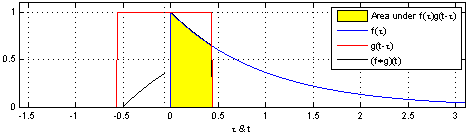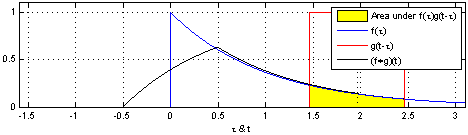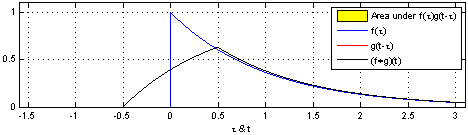출처 : https://en.wikipedia.org/wiki/Convolution

Convolution 연산은 교환 법칙, 결합 법칙, 분배 법칙이 성립한다.

Convolution은 Fourier Transform과도 관련이 있다. (Convolution Theorem)

Convolution $(f*g)(t)=\int_{-\infty}^{\infty}f(\tau)g(t-\tau)d\tau$
Fourier Transform $\mathcal F\{f(t)\}=\int_{-\infty}^{\infty}f(t)e^{-j2\pi ut}dt$

$f$ 와 $g$ 의 convolution을 fourier transform하면, 각 함수를 fourier transform하고 곱하는 것과 같다. 즉, 시간(공간) 영역에서 convolution이 주파수 영역에서의 곱셈과 같다는 것이다.

\mathcal F\{(f*g)(t)\}=\int_{-\infty}^{\infty}[\int_{-\infty}^{\infty}f(\tau)g(t-\tau)d\tau]e^{-j2\pi ut}dt

\mathcal F\{(f*g)(t)\}=\int_{-\infty}^{\infty}f(\tau)[\int_{-\infty}^{\infty}g(t-\tau)e^{-j2\pi ut}dt]d\tau

\int_{-\infty}^{\infty}g(t-\tau)e^{-j2\pi ut}dt=\mathcal F\{g(t-\tau)\}=\mathcal F\{g(t)\}e^{-j2\pi u\tau} \;이므로\\ \quad \because x(t) \Leftrightarrow X(w), \;x(t-a) \Leftrightarrow e^{-j2\pi ua}X(w) \quad : \;fourier\; transform\; transition

\mathcal F\{(f*g)(t)\}=\mathcal F\{g(t)\}\int_{-\infty}^{\infty}f(\tau)e^{-j2\pi u\tau}d\tau

\mathcal F\{(f*g)(t)\}=\mathcal F\{g(t)\}\mathcal F\{f(t)=G(u)F(u)

(3) 2-D convolution

이제 이미지를 처리하기 위한 2차원으로 확장해볼 수 있다. 독립 변수 2개의 함수로 표현되는 신호 $x([m,n])$ 을 2차원 신호라고 하고, 인덱스는 공간상의 위치를 의미한다.

LTI system에서 1D-convolution으로 나아갔듯이, Linear Shift-invariant(LSI) system에서 2D-convolution으로 나아갈 수 있다.

Shift-Invariant $y([m,n])=H\{x[m,n]\}$ $y([m-m_0,n-n_0])=H\{x[m-m_0,n-n_0]\}$

1D와 마찬가지로, impulse signal을 통해 신호를 표현할 수 있다.

x[m,n] = \sum_{k=-\infty}^{\infty}\sum_{l=-\infty}^{\infty}x[k,l]\delta[m-k][n-l]

또한 2차원 Impulse signal를 LSI 시스템의 입력으로 가하면 Impulse response을 얻을 수 있다.

h[m,n] = H \{\delta[m,n]\}

그러면 linear system과 shift-invariant system의 특성으로 인해 다음의 2D-convolution을 정의할 수 있다.

y[m,n]=H\{x[m,n]\}=H\{ \sum_{k=-\infty}^{\infty}\sum_{l=-\infty}^{\infty}x[k,l]\delta[m-k,n-l] \}

y[m,n]= \sum_{k=-\infty}^{\infty}\sum_{l=-\infty}^{\infty}x[k,l]H\{\delta[m-k,n-l] \} \quad \because linear

y[m,n]= \sum_{k=-\infty}^{\infty}\sum_{l=-\infty}^{\infty}x[k,l]h[m-k,n-l] \quad \because time\;invariant

y[m,n]= h[m,n]*x[m,n] = \sum_{k=-\infty}^{\infty}\sum_{l=-\infty}^{\infty}x[k,l]h[m-k,n-l]

간단하게 아래의 5x5 matrix input과 3x3 filter의 convolution을 계산해보자. $h[m,n]$ 을 뒤집고, 모든 x의 index에 대해서 필터를 곱하고 더하면 결과를 얻을 수 있다.

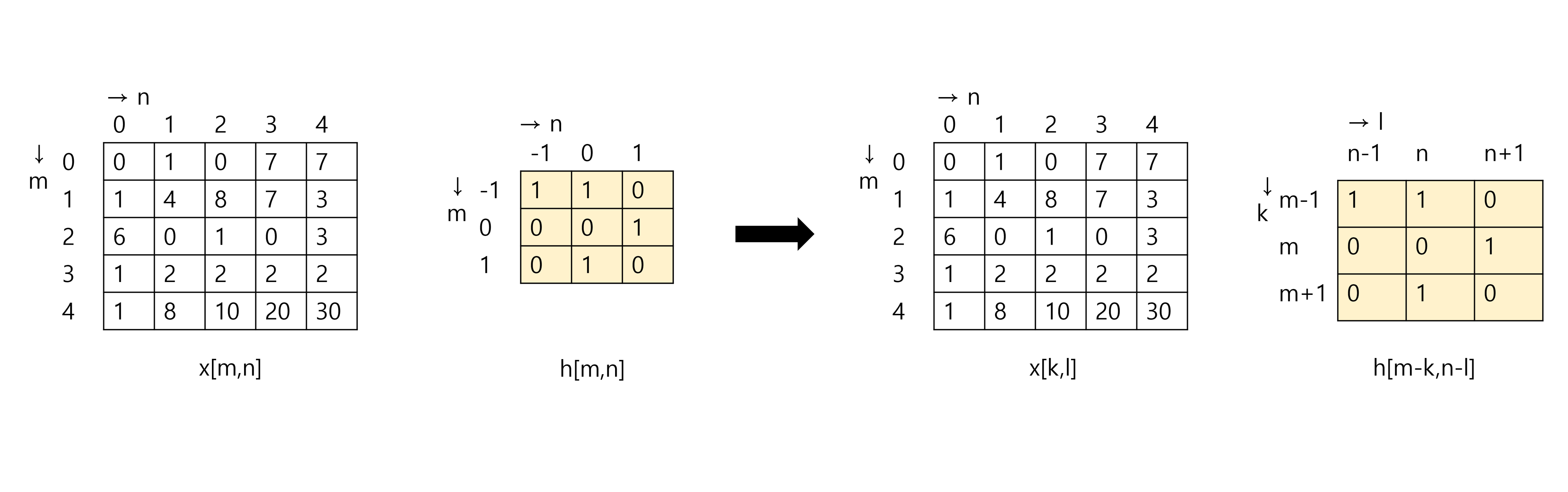
간단한 계산을 통해 구한 최종 출력 신호는 아래와 같다.

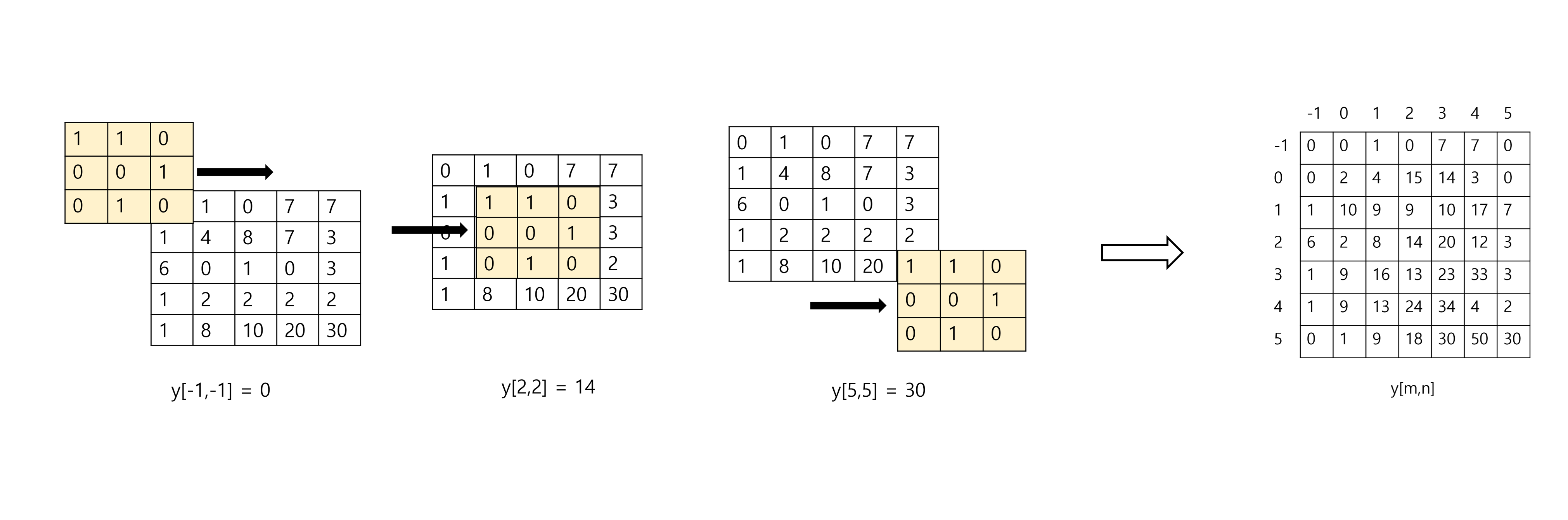
(4) Simple example

이미지 프로세싱에서 우리는 convolution을 이용해 어떤 이미지 입력을 넣었을 때, 원하는 출력을 얻고자 하고, convolution에 사용되는 필터를 설계한다는 것은 LSI 시스템의 impulse response $h[m,n]$ 을 결정하는 것과 같다고 할 수 있다.

몇 가지 간단한 필터를 이미지에 적용하여 결과를 보자.

아래는 python numpy를 이용해 구현한 convolution이다.

def convolution(x, f, stride=1, pad=0):
    """
    Image(x) : (height, width)
    Filter(f) : (height, width)
    """
    ##  데이터 shape
    h, w = x.shape
    f_h, f_w = f.shape

    # padding과 stride를 이용하여 output shape를 미리 계산할 수 있다.
    out_h = (h + 2 * pad - f_h) // stride + 1
    out_w = (w + 2 * pad - f_w) // stride + 1

    # padding : channel에는 더하지 않고, h와 w에 pad만큼 
    x = np.pad(x, [(pad, pad), (pad, pad)], 'constant')
    out = np.zeros((out_h, out_w))
    
    # h 방향(아래 방향)과 w방향(오른쪽 방향)으로 stride만큼 움직이면서
    # matrix element-wise multiplication 후 sum
    for _h in range(out_h):
        h = _h * stride
        for _w in range(out_w): 
            w = _w * stride
            out[h, w] = np.sum(x[h:h+f_h, w:w+f_w] * f)
    return out

저주파 통과 필터 : 필터의 중심점을 기준으로 주변 픽셀의 평균값을 계산

_filter = np.array([[1/10,1/10,1/10],
                   [1/10,1/10,1/10],
                   [1/10,1/10,1/10]])
img_processed = convolution(img, _filter)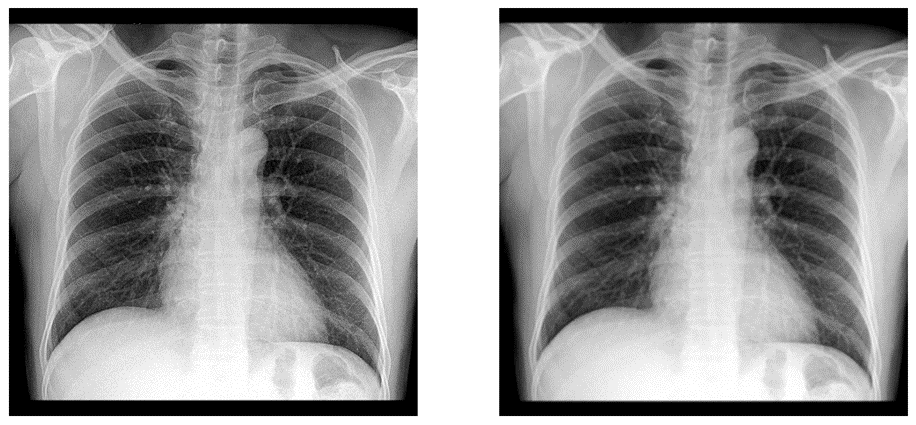

고주파 통과 필터 : 윤곽선을 추출

_filter = np.array([[1,1,1],
                    [1,-10,1],
                    [1,1,1]])
img_processed = convolution(img, _filter)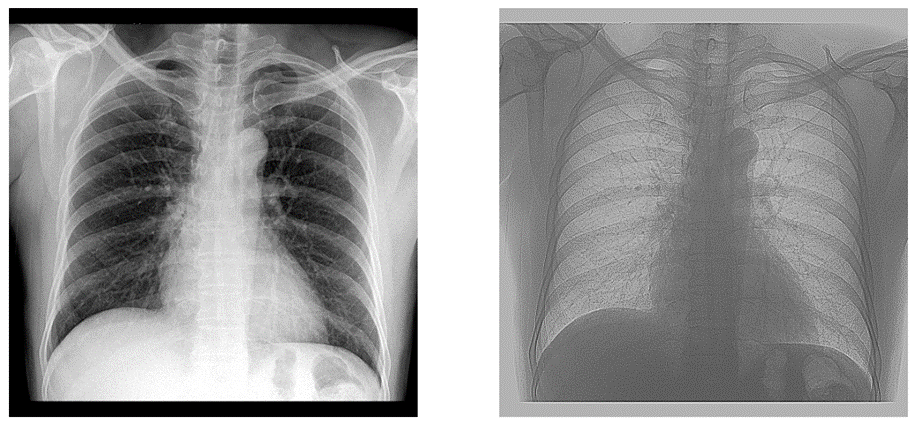

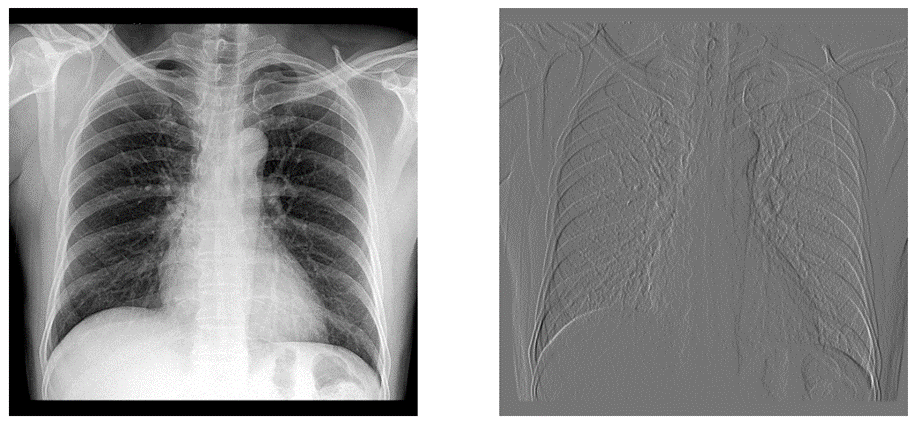
가로선 / 세로선 검출 필터: 세로 / 가로방향 픽셀 차이를 계산

_filter1 = np.array([[-1,-1,-1],
                     [0,0,0],
                     [1,1,1]])
_filter2 = np.array([[-1,0,1],
                     [-1,0,1],
                     [-1,0,1]])
img_processed = convolution(img, _filter1)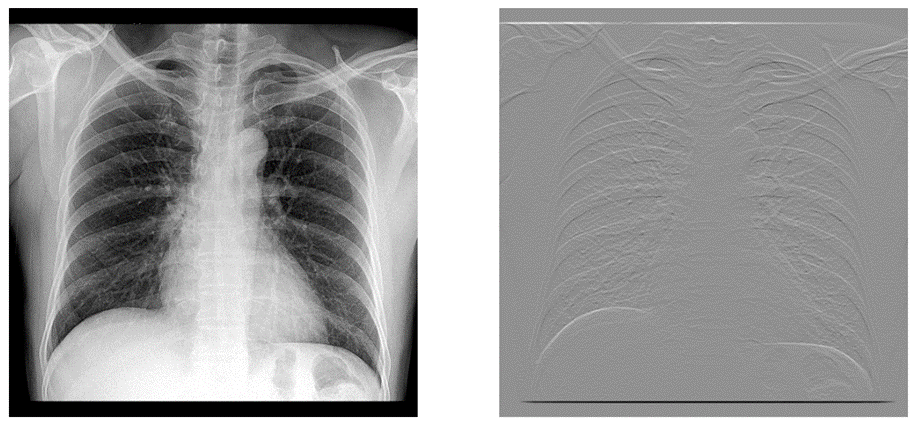

2. Convolutional Neural Network

(1) Introduction

Convolutional Neural Network는 vision deep learning에서 기본이 되는 네트워크이다. 실제로 인간이 어떤 물체를 시각적으로 인식하는 것과 유사하게, 각각의 필터가 local receptive field를 가지고 특정 패턴을 추출하도록 하고, 저수준의 패턴(edge, blob ...)을 기반으로 고수준의 패턴(texture, object ...)까지 특징을 파악하도록 설계되었다.

기존의 fully connected layer에서는 이미지 데이터를 다룰 때, (C,H,W)의 이미지 데이터를 1차원으로 펼쳐서 입력으로 사용하였다. 이렇게 할 경우, 데이터의 공간적인 정보가 사라진다는 것이 단점이 될 수 있다. 또한 하나의 특징을 추출하기 위해 (C $\times$ H $\times$ W)개의 가중치가 필요하여 연산에 대한 부담이 컸다.

반면에 CNN은 데이터의 기존의 구조를 유지시킨 상태에서 연산을 수행하므로 공간적인 정보가 다음 layer로 전달될 수 있다. 즉, 3차원 데이터(H, W, C)를 입력으로 받고, 3차원 데이터를 출력으로 하여 다음 layer로 전달한다. 추가적으로 하나의 filter가 하나의 특징을 추출하게 되므로 연산량도 크게 줄일 수 있다. (필터는 보통 작은 수용 영역을 가지므로 이미지를 flatten한 것보다 훨씬 작은 가중치를 사용할 수 있다.)

(2) Implementation

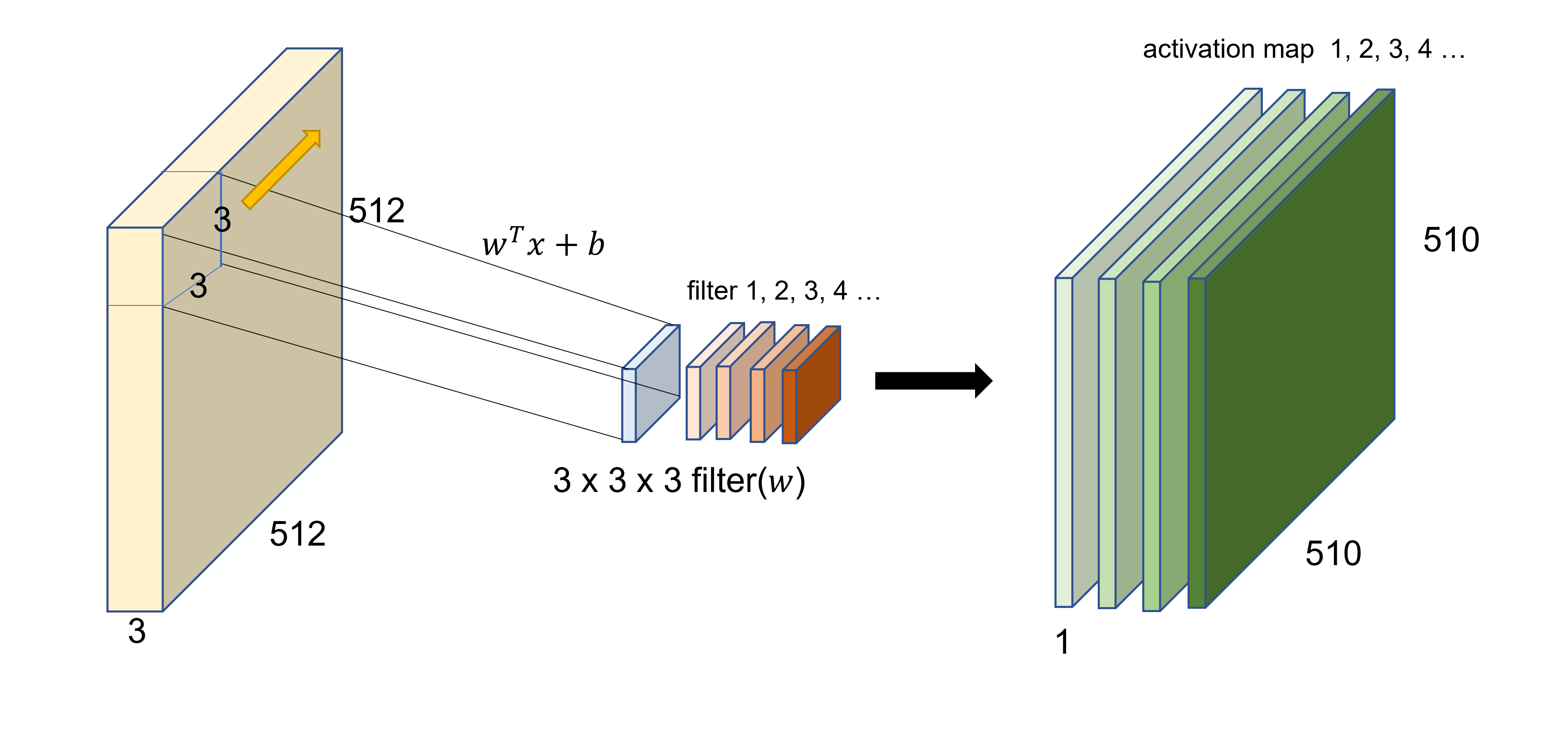
위의 그림과 같이 작은 필터를 두고, 이를 이미지에 대해 슬라이딩 시키면서 내적 연산을 하여 결과 값을 추출한다. 이때 필터의 channel은 입력값의 channel와 같은 깊이를 가져야 하며, 전체 channel 깊이에 대해 내적 연산을 하게 된다. 기본적으로 filter를 이미지 위에 겹쳐놓고 element-wise multiplication ( $w^Tx + b$ ) 한다고 생각할 수 있다. 각 channel별로 합성곱 연산을 진행하여 모두 더해주면 된다. (하나의 필터가 다수의 channel을 가지고 있다고 해서 여러 개의 feature map이 나오는 것이 아니고, 각 channel별로 다른 가중치로 연산하고 이를 모두 더해서 하나의 결과를 낸다.)

이 내적 연산은 두 벡터(텐서)가 유사할수록 더 큰 값을 출력하게 되므로, 필터는 이미지 내부에 있는 어떤 패턴을 추출(feature map extraction)하기 위해, 그 패턴과 유사한 형태의 벡터를 가지도록 학습된다고 할 수 있다.

즉, CNN layer에서 하나의 필터를 이용해 하나의 feature map (activation map)을 생성할 수 있고, 여러 개의 filter를 사용하여 여러개의 feature map을 추출해 낼 수 있다. 그러므로 우리가 지정하는 filter의 갯수를 통해 output activation map의 channel 수를 정할 수 있다.

CNN에서의 합성곱이 위에서 배운 2D-convolution과 다른 점은, 정확하게 이야기하면 여기서 사용하는 연산은 convolution이 아닌 cross-correlation이다. cross-correlation은 원래 두 신호의 유사성을 측정하는데 사용된다. 하지만 실제로 cross-correlation은 수식을 봤을 때, convolution에서 하나의 함수를 반전시키는 것 말고 다른 것이 없다. 그러므로 필터를 뒤집지 않고 이동시키며 계산한다고 볼 수 있다. CNN에서는 필터의 값을 학습하는 것이 목표이기 때문에 처음에 가중치 값을 초기화하므로, 필터를 뒤집거나 뒤집지 않거나 결과상에 차이가 없기 때문에 convolution 대신에 cross-correlation을 사용한다.

Convolution : \;y[m,n]= \sum_{k=-\infty}^{\infty}\sum_{l=-\infty}^{\infty}x[k,l]h[m-k,n-l]

Cross\;correlation : \;y[m,n]= \sum_{k=-\infty}^{\infty}\sum_{l=-\infty}^{\infty}x[k,l]h[m+k,n+l]

CNN에서 합성곱 연산을 할 때, 필터를 움직이는 간격을 stride라고 하고, 반복적으로 합성곱 연산을 할 때, 입력보다 출력이 작아지는 것을 방지하고자 이미지 밖으로 0으로 채우는 것을 padding이라고 한다.

정리하자면 하나의 layer에서 합성곱을 실행한다고 했을 때, 아래와 같은 상황을 가정하자.

Input image : $W_1$ , $H_1$ , $C_1$
Filter size : $F \times F$
Number of filters : $K$
stride : $S$
padding : $P$

결과적으로 출력 데이터의 shape과 가중치의 수는 다음과 같다.

Output feature map width : $W_2 = \frac{(W_1-F+2P)}{S} +1$
Output feature map height : $H_2 = \frac{(H_1-F+2P)}{S} +1$
Output feature map channel : $C_2 = K$
Number of learnable parameters : $F^2 \times C_1 \times K$ ( $+\;K$ , bias를 고려한다면)

(3) Properties of CNN

Vision task에서 Convolutional Neural Network를 어떠한 관점에서 이해하면 좋을지, 또한 왜 작동을 잘 하고, 많이 사용되는지 생각해보자.

머신 러닝 알고리즘은 우리가 원하는 함수를 학습하고, 학습에 사용한 데이터를 넘어 일반화하기 위하여 모델에 어떠한 Inductive Bias를 사용한다.

머신 러닝 알고리즘이 갖는 큰 문제로는 (1) 입력 데이터가 조금 바뀌었을 때 결과가 많이 바뀌는 것 (2) 데이터를 이해하고 학습하는 것이 아니고 결과와 편향을 학습하는 것이 있다. 우리는 이 경우 모델이 일반화되지 못했다고 이야기 한다. 여기서 Inductive bias는 학습 시에 만나보지 못한 데이터에 대하여 더욱 정확한 예측을 하기위해 사용하는 추가적인 가정, 즉, 모델의 일반화에 도움을 주는 가정이라고 할 수 있다.

딥러닝 모델들은 대부분 특정 데이터를 잘 다루기 위해 어떠한 가정 하에 설계가 된다. CNN은 이미지 데이터를 잘 일반화시키기 위해 이미지가 가진 특성에 따른 몇 가지 inductive bias를 포함하여 그 구조가 설계되었으며, 이로 인해 해당 task에서 좋은 성능을 보여줄 수 있는 것이다.

이미지 데이터가 가진 특성과 이에 대한 CNN의 가정에 대해 살펴보자.

(1) Stationary of statistics
어떤 데이터의 통계적 속성이 stationary하다는 것은 시간 또는 위치에 관계 없이 동일한 패턴이 반복된다는 것이다. 이미지 데이터가 stationary하다는 것은 이미지의 특정 위치에 있는 패턴이 다른 위치에서 똑같이 발견될 수 있다는 것으로 해석할 수 있다.

이미지 내부에서 우리가 원하는 물체는 서로 다른 위치에 존재할 수 있다. 각각 모양이 조금씩 다를 수 있지만 대부분 어떤 비슷한 통계적 특성을 가질 것이다. 이러한 특성을 추출하기 위해서 서로 다른 위치에 있는 물체에 대해 서로 다른 필터를 적용하는 것 보다는 하나의 필터로 공통적인 특성을 추출해낼 수 있다면 훨씬 효율적일 것이다.

Parameter sharing
CNN은 하나의 작은 필터가 이미지 위로 이동하면서 내적을 수행하는 parameter sharing의 성질을 가지고 있다. 즉, 이미지의 위치에 상관이 없이 어떠한 동일한 패턴을 추출하려는 목적을 달성하기에 하나의 파라미터 값을 이미지 전체에 공유하여 내적하는 해당 convolution 연산은 stationary 가정에 아주 잘 맞는다고 할 수 있다.
Translation Equivalance
이미지 내부의 위치와 상관없이 동일한 특징 혹은 패턴이 존재한다는 stationary가정을 바탕으로 CNN은 필터의 parameter를 공유하여 이미지 전체에 대해 하나의 feature map을 추출하기 때문에 자연스럽게 translation equivalance 특성으로 이어질 수 있다. 이는 이미지 내부에 검출하고자 하는 패턴이 바뀌면, 출력도 그대로 바뀐다는 것을 의미한다.
예를 들어 아주 잘 설계된 필터가 있어서 내가 원하는 패턴을 모두 검출할 수 있다고 하자. 그렇다면 이 패턴이 다른 곳에 위치하더라도 convolution 결과 또한 바뀐 영역의 패턴을 검출해낼 것이다.
Translation Invariance
equivalance와 invariance는 말그대로 반대의 의미를 갖기 때문에 CNN이 두 특성을 모두 가진다는 것은 조금 이상하게 들릴 수도 있다. 하지만 실제 CNN을 사용할 때 사용되는 Max-pooling기법과 activation function(softmax 등)으로 인해 translation invariance 특성, 즉 이미지 내부 어떤 물체의 위치가 바뀌어도 같은 결과를 내놓게 된다.

Translation equivalance와 Translation Invariance를 이해하기 위해 간단한 예시를 들어보자. 먼저 입력 이미지는 6x6의 이미지라고 하고, 간단한 예시로 우리가 검출하고자 하는 패턴이 아래와 같이 이미지에 포함되어있다고 해보자. (1 행의 입력 이미지는 원하는 패턴이 오른쪽 아래에, 2 행의 입력 이미지는 원하는 패턴이 왼쪽 위에 위치)

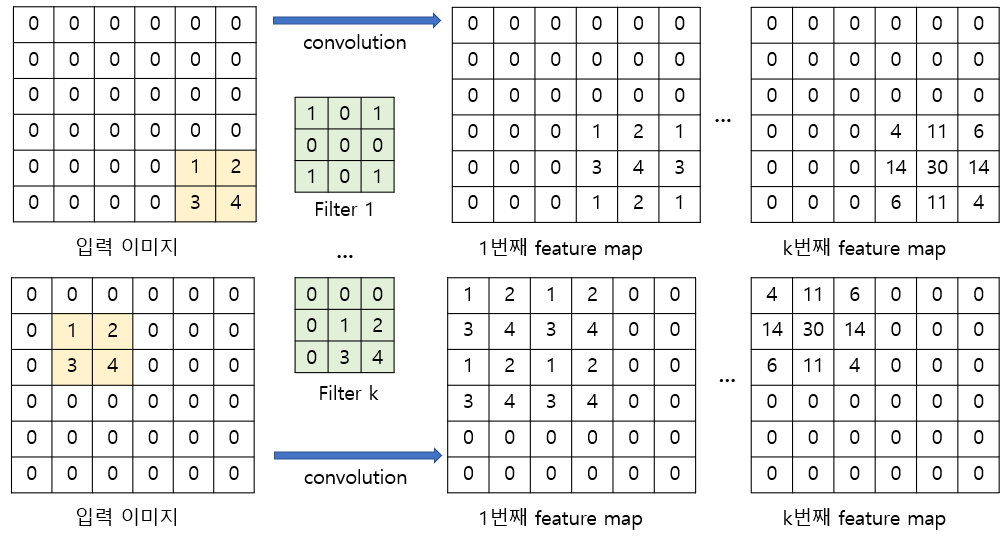
위 그림은 검출하고자 하는 패턴의 위치 바뀌었을 때, convolution의 결과가 바뀌는 equivalance를 잘 보여준다. 하지만 여러개의 필터를 사용하고, 여러 개의 class를 예측하려고 하는 일반적인 분류 문제로 확장을 해보자. CNN을 이용한 이미지 분류 문제에서는 보통 Convolution layer와 pooling layer를 통해 특징을 추출하고, 1-dimensional vector로 flatten한 뒤, fully-connected layer와 activation function을 이용해 각 class의 probability를 예측한다.

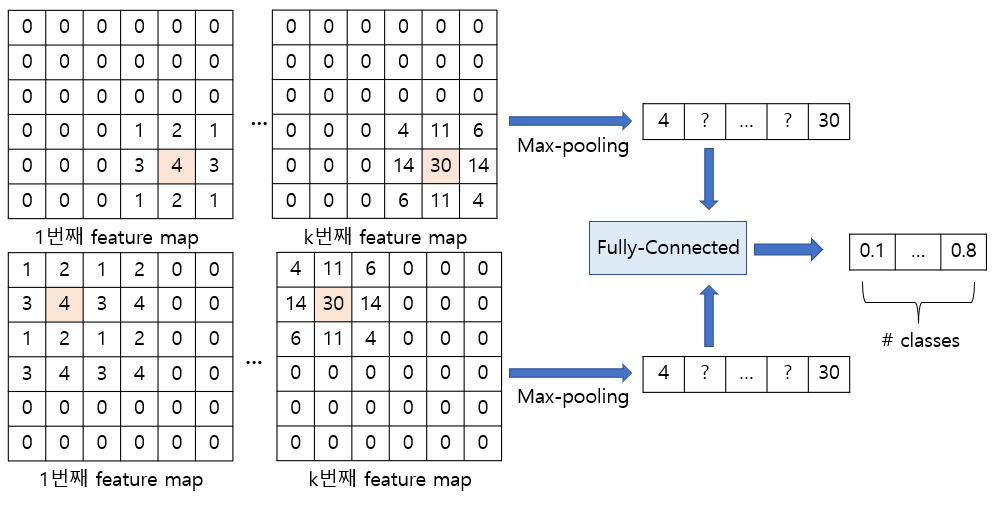
1행과 2행의 입력 이미지는 서로 다른 위치에 같은 패턴을 가지고 있었다. 이때 convolution 연산 자체는 translation equivalance하기 때문에 feature map 상에서 각 특징이 서로 다른 위치에 출력되었다. 하지만 convolution layer, max-pooling, fully-connected layer, soft-max를 거친 후, 최종 확률이 같게 도출된다는 것을 알 수 있다. 즉, CNN에서는 이미지 내부에서 찾고자하는 물체가 어디에 있던 상관없이 network의 output은 동일하게 나온다고 할 수 있고, 이를 translation invariance 특성이라고 한다.

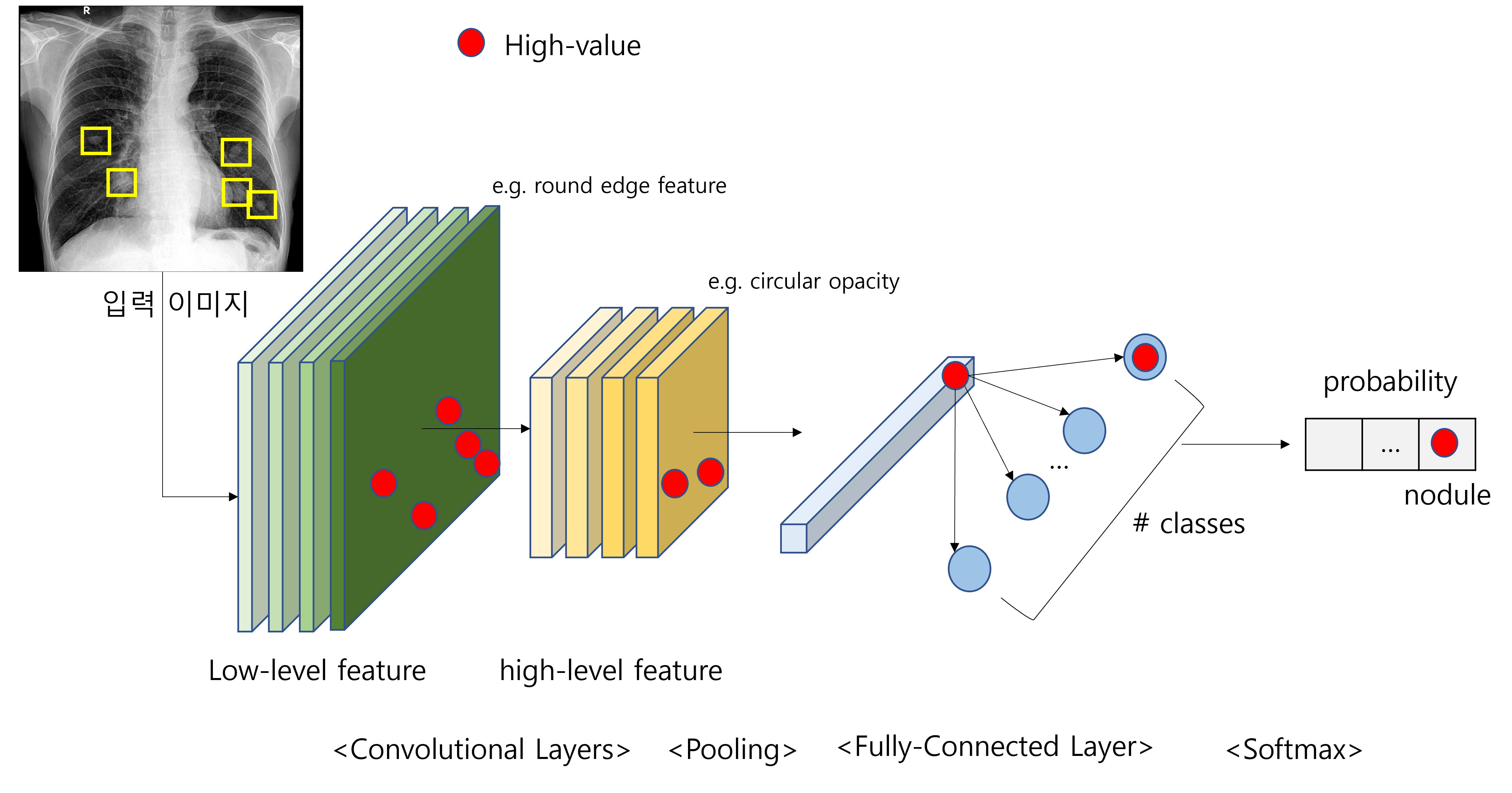
더욱 직관적인 이해를 위해 아래의 x-ray 이미지에서 폐 영역에 있는 폐 결절이 있는지 없는지 구별하는 네트워크를 생각해보자.

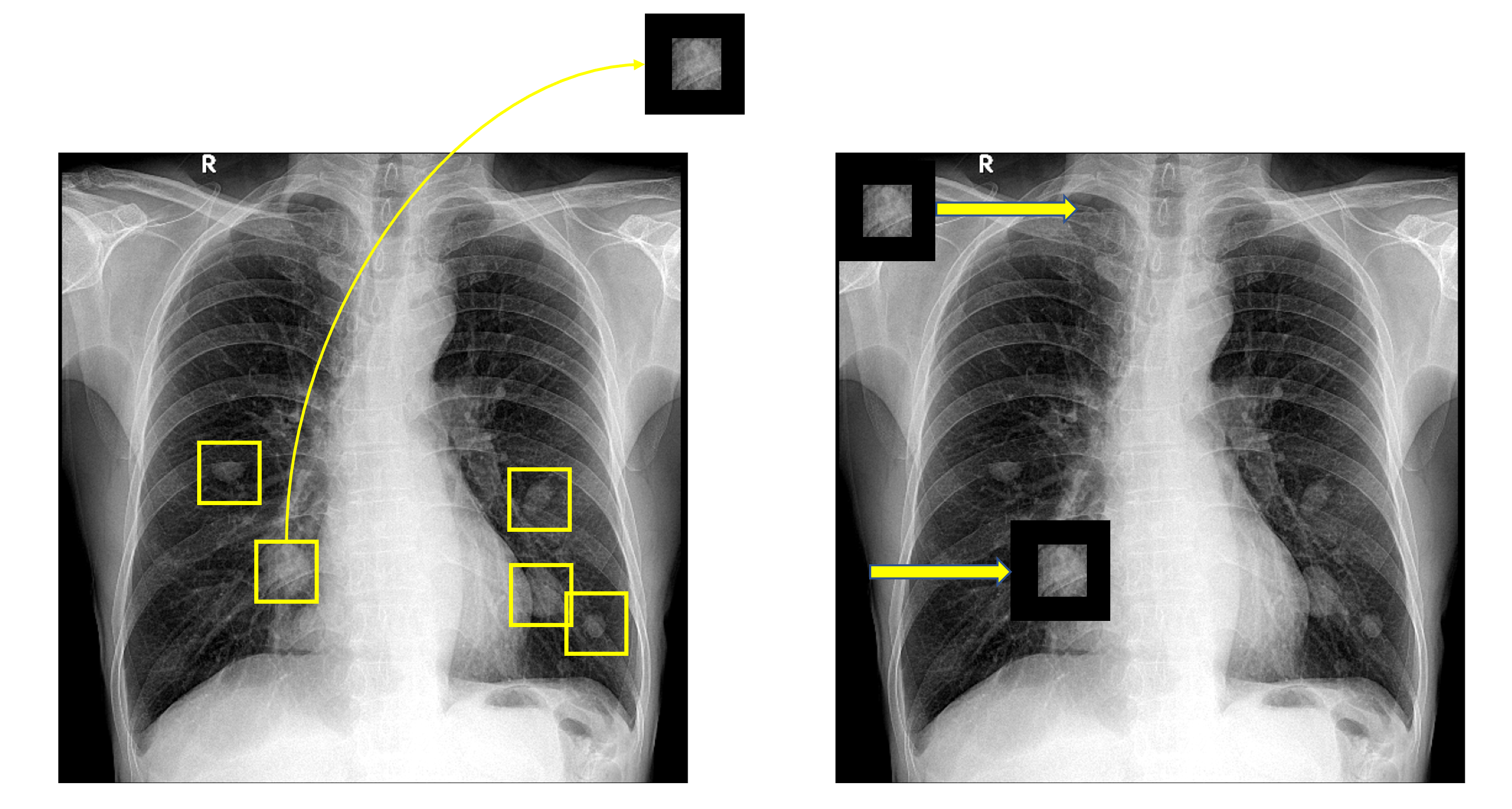
노란색 박스로 친것처럼 현재 비슷하게 생긴 몇 개의 폐 결절이 존재하는데, 이를 어떻게 검출할 수 있을까? 그림에서는 간단하게 하나의 결절과 똑같이 생긴 필터로 예시를 들었지만, 잘 설계된 필터, 즉 폐 결절을 설명할 수 있는 대표적인 필터 벡터를 가지고 있다면, 이 필터를 이미지 전체에 대해 convolution함으로써 우리는 원하는 패턴을 추출해낼 수 있을 것이다. 하지만 실제로 하나의 필터만을 이용해서 이 task를 해내는 것은 어렵고, CNN에서는 더 많은 channel과 여러 겹의 cnn layer, non linear function등을 사용하여 더 복잡한 연산을 함으로써 더욱 정교한 필터를 학습하고, 양질의 feature를 추출하여 이 작업을 해낼 수 있을 것이다.

(2) Locality of pixel dependencies
이미지의 locality라 함은 서로 가까운 pixel들끼리 더욱 관계가 있다는 것을 의미한다. 이미지는 여러 가지 특성들로 구성되며 이 특성은 이미지 전체가 아닌 local한 영역의 일부 픽셀들로 구성되므로, 픽셀들 사이의 종속 관계도 작은 영역 내부에서 정의된다는 뜻이다.

이미지의 locality 또한 CNN에서 작은 필터를 이용하여 local 영역의 특성을 추출하는 동시에, 입력 이미지 전체와 상관없이 local하게 연산이 들어가므로 convolution연산과 매우 잘 들어맞는다는 것을 알 수 있다.

Convolution의 의미와 Convolutional Neural Network의 특징에 대해 간단히 알아보았다. 다음에는 실제 네트워크에 사용되는 convolution 연산은 어떻게 발전해왔는지 살펴보려고 한다.

신희준

공부하고 싶은 사람

이전 포스트

Kernel machine basic

다음 포스트

Classification Performance Metric

1개의 댓글

김한주

2022년 11월 28일

대단한 자료 감사합니다

답글 달기