Paper : Multiplicative Fourier Level of Detail (Yishun Dou, Zhong Zheng, Qiaoqiao Jin, Bingbing Ni / CVPR 2023, Highlight)
- Motivation : Instant-NGP를 공부하다가 더 최근에 나온 연구로, Multiresolution hash encoding에 fourier feature transformation 및 combination을 더하여 더 좋은 성능을 보여줬다. Implicit Neural Representation는 Neural network 자체에 하나의 정보를 저장하는 방법으로, 이러한 정보를 어떠한 형태?로 저장하느냐에 따라 표현할 수 있는 정보의 질과 양이 천차만별인 것 같다. 글 자체를 잘 써줘서 INR의 역사를 공부하기가 참 좋았다.
Short Summary
- Feature volume based INR을 새로운 방식으로 정의
- Multi-level feature의 linear combination을 이용한 sum of sines으로 신호를 표현
- Fourier analysis가 가능했고, 더욱 나은 성능 달성
Introduction
computer graphics에서 기존의 gemertric modeliing은 signal을 grid-based format의 discrete sample에 저장하는 방식을 택했다.
그런데 이런 방식은 미분이 불가능하기 때문에 learning-based framework에 적용하기가 힘들었는데, Neural implict function (INR)이 등장하면서 이를 해결해주었다.
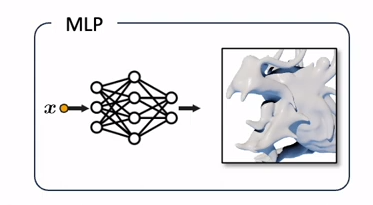
이러한 INR은 기본적으로 아래와 같이 좌표 를 받아 해당 좌표의 정보를 저장하는 방식을 택했는데,
(나는 INR의 "implicit"을 어떠한 정보를 표현함에 있어서 각 좌표 의 값을 모두 저장하는 방식이 아니라, 어떤 함수를 통해 간접적으로 표현 ()한다는 의미로 이해했다.)
이전에 계속 언급했던 것처럼 (On the Spectral Bias of Neural Networks (Nasim Rahaman, Aristide Baratin, Devansh Arpit, Felix Draxler, Min Lin, Fred A. Hamprecht, Yoshua Bengio, Aaron Courville / PMLR 2019)) INR은 low frequency spectral bias로 인해 high frequency detail을 recover하기 어렵기 때문에 NeRF 처럼 positional encoding 등을 사용하곤 했다.
NeRF 말고도 비슷한 관점으로 접근한 몇 연구들이 있는데 (SIREN, FFN, MFN, 등), 이러한 연구들은 모두 아래와 같은 비슷한 concept를 가지게 된다.
는 학습 가능한 parameter (), 는 point coordinate sinusoidal bases로 이루어진 fourier feature를 생성. (서로 다른 input coordinate가 orthogonal한 sin 함수를 만들어내고 있음)
이 feature가 MLP weight 를 통해 선형 결합되면서 output 을 출력하는 것
저자들은 이러한 approach는 다음의 문제를 가지고 있다고 지적한다.
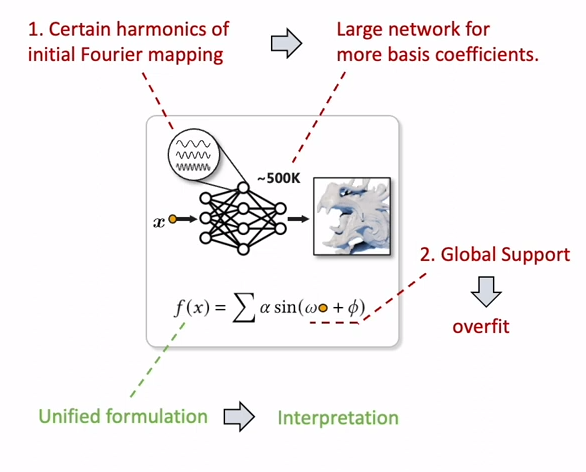
1) 여기서 training은 sinusoidal bases의 coefficient 를 배우는 것이 되는데, 이러한 basis coefficient를 모두 학습하는데는 너무 큰 network를 필요로 한다.
2) Fourier bases가 infinite global support를 가지기 때문에 overfitting되기가 쉽다. infinite global support를 가진다는 것은 각각의 base function (ex. )가 space 전체의 value에 영향을 끼친다는 것인데, 이렇게 되면 local detail change가 전체 fourier coefficient에 영향을 미치게 된다는 것이고, local small changes에 sensitive 해지면서 high-frequency noise 등에 overfitting 되기가 쉬워진다는 것이다.
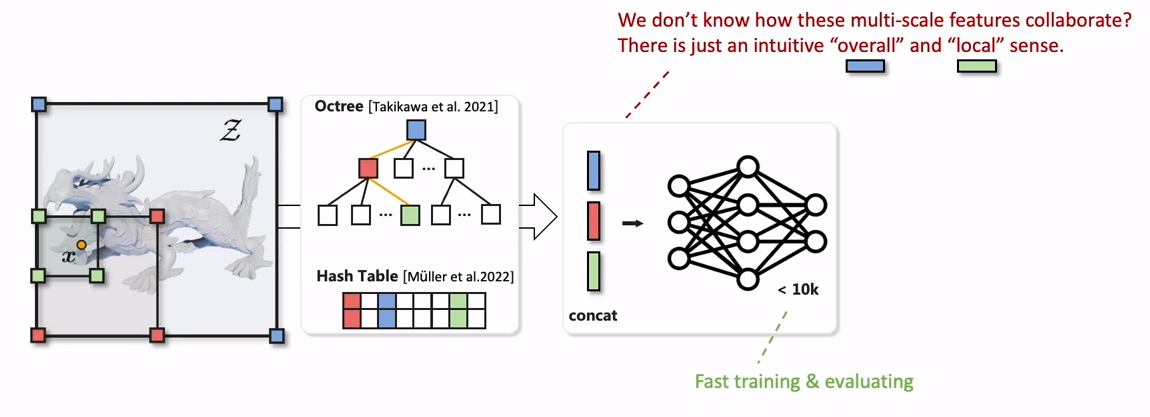
이러한 문제를 해결하기 위해서 최근에는 local-detail을 잘 학습하기 위해 multi-level feature를 사용하는 hybrid representation이 많이 사용되게 되었다. (이전 리뷰 Instant Neural Graphics Primitives with a Multiresolution Hash Encoding)
Hybrid representation은 다양한 resolution에서 정의된 feature를 query한 결과를 합쳐서 같이 input으로 사용하는 방법을 택했고, 이를 통해 overall/local detail을 같이 잘 학습할 수 있었고, 이로 인해 더 작은 MLP를 decoder로 사용할 수 있었으므로 빠른 학습이 가능했다.
하지만 이 방법같은 경우에 이러한 multi-scale feature에 대한 정보가 내부적으로 어떻게 합쳐져서 최종적인 output을 내는지 해석하기가 쉽지 않다.
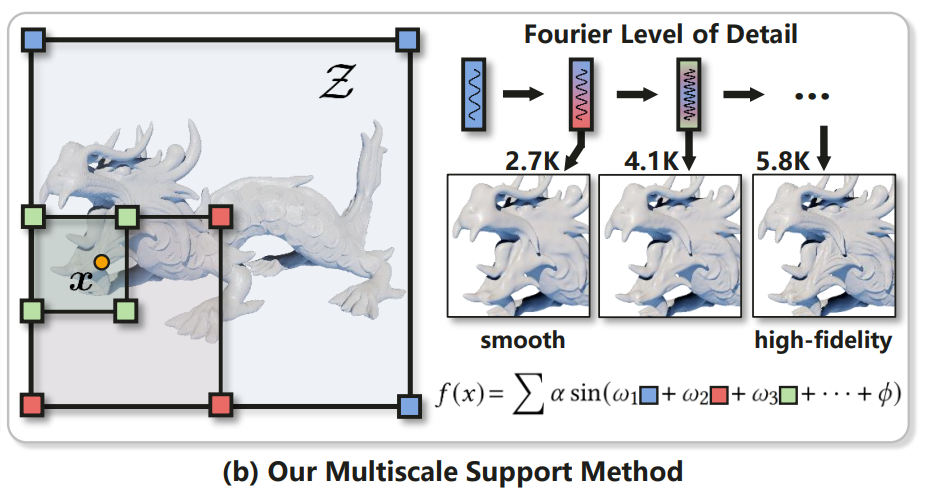
이 논문은 Hybrid representation의 장점을 모두 취하면서도, 한 단계 더 나아가 fourier basis function을 이용하여 각 LOD (Level of Detail)에 대해 frequency bandwidth의 control이 가능한 framework를 제안하였다.
즉, fourier feature를 사용하는데 있어서, 그 coordinate에 대한 표현 자체도 multi-scale feature의 interpolation으로 사용한다는 것.
이 구조는 coarse level의 smooth overall shape과 fine level의 high-fidelity detail을 아주 잘 표현할 수 있게 해준다고 한다.
- Level of Detail이란 computer graphic에서 카메라와 mesh사이의 거리 (중요도)에 따라서 mesh grid의 정밀도를 조정하는 기법을 말한다. 즉, 여기서는 frequency band limitation을 이용해 coarse level에서는 smooth하게 표현하여 computational cost를 낮추고, fine level에서는 더 detail을 집중할 수 있도록 해주는 것으로 볼 수도 있겠다.
- Random Fourier Feature는 random fourier bases를 이용해 input data를 더 높은 차원의 space로 mapping하는 정도로 이해할 수 있을 것 같다. 여러 frequency를 random sampling해가면서 kernel function의 feature space를 approximate한다. Kernel machine 공부
Method
Multiplicative Fourier Level of Detail
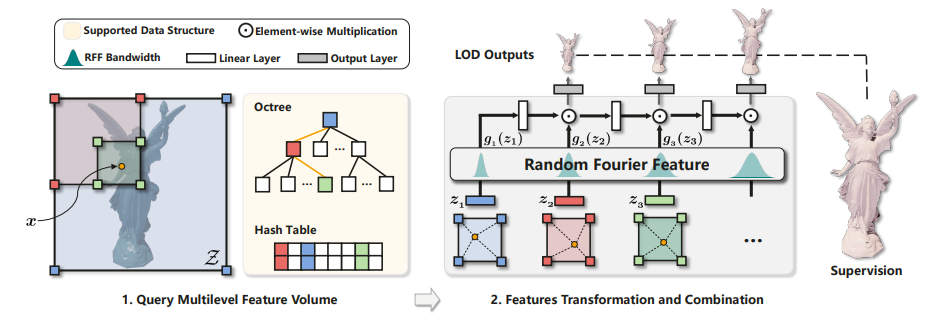
아래의 그림은 MFLOD method를 도식화한 것이다.
(1) Query Multilevel Feature Volume
MFLOD는 먼저 feature volume을 base로 하며, 이는 Instant-NGP랑 비슷한 방식으로 tree-structured multi-level feature grid (feature volume )를 정의한다.
각 Voxel은 -dimension의 learnable parameter를 갖는 8개의 corner를 포함하게 된다.
그리고 feature-volume 의 각 level 은 하나의 LOD를 의미하게 된다.
위 그림처럼 하나의 과 LOD level 이 주어지면, 가장 큰 level 1부터 까지 를 포함하는 모든 voxel 을 찾고, 각 level에서 voxel의 8개의 corner에 대해 trilinear interpolation을 해서 per-voxel shape vector 를 계산한다.
(2) Transformation and Combination
Multi-resolution feature를 뽑은 후에는 이를 합쳐줘야 하는데, 이전의 방법들은 이를 합치거나 concat해서 MLP와 non-linear activation으로 decode했다.
하지만 이 연구에서는 이전의 "aggregate-decode" paradigm을 "transform-combine"으로 대체하여 Fourier analysis에 대한 LOD representation의 강점을 부각시키려 하였다.
먼저, grid interpolation 후에 layer normalization을 해주고, 각 level의 feature는 learnable filter parameter를 이용해 sinusoidal transformation을 해준다. (Random Fourier Feature)
여기서 는 grid feature dimension이고, 은 mapping dimension
- Layernorm은 아래 그림과 같이 각 instance (input)의 feature를 모든 channel에 대해 normalize하는 방식으로 spectral manipulation을 더 잘하기 위해 사용한다고 한다.
저자들은 이런 sinusoidal filter가 자연스럽게 Random Fourier Feature representation과 연결되기 때문에 이렇게 변환된 representation을 Fourier LOD로 부른다고 한다.
그 후 각 level의 Fourier LOD를 elementwise multiplication ()과 FC layer로 이루어진 network를 통해 layer to layer로 recursive하게 combine된다.
Network의 parameter는 가 된다.
결과적으로는 각 level에 대한 output을 해당 level 전의 모든 feature를 사용하는 sum of sines로 표현할 수 있다. (coefficient , , 는 filter parameter와 network parameter로 정해지는 값)
위 식을 보면 각 level에서 개 만큼의 sine term의 합으로 표현이 되는 것을 알 수 있는데, 이는 항을 통해 의 sine terms의 수가 exponential하게 늘어나고, elementwise multiplication과 bias ()를 통해 sine term이 두 배 더 늘어난 것이다.
각 sine term이 저런식으로 표현된 것은 간단한 삼각법 계산으로 증명될 수 있다. (product of two sines can be transformed to the sum of two sines.)
즉, LOD level 의 sine term의 수는
결론적으로, 번째 level의 fourier feature가 주어지면, 이 feature는 이전의 coarse feature들과 모든 sinusoidal term에 대해 선형적으로 결합된다. 이러한 feature는 각각 multi resolution feature를 기반으로 만들어졌으므로, fine level에서는 모든 function을 활용해서 local high-frequency detail을 잘 reconstruct할 수 있게된다.
Spectrum Analysis
MFLOD에서는 initialization이 매우 중요하다고 한다.
먼저 feature volume 는 아주 작은 randomness를 가지는 uniform distribution으로 initialize한다.
Sinusoidal filter는 각 level마다 다른 bandwidth를 갖도록 initialize한다. (은 hyperparameter)
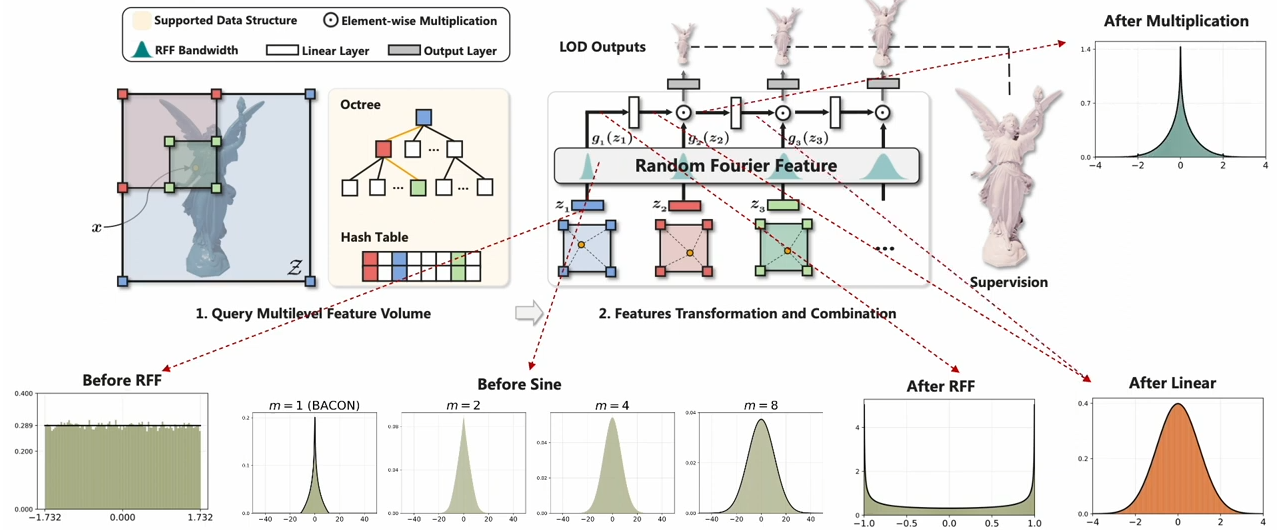
순서대로 보면, sin함수에 들어가기전에 는 uniform distribution이고, 라고 하면 일 대 의 확률밀도함수는 아래와 같다고 한다. (Bacon: Band-limited coordinate networks for multiscale scene representation <- 이거를 또 공부해야할거같다.)
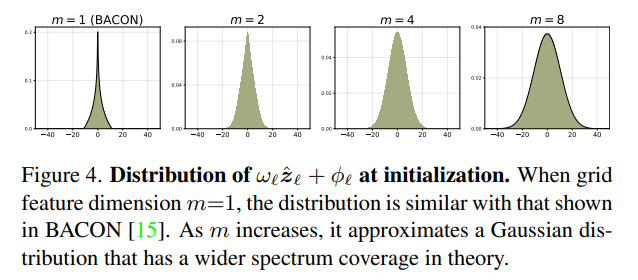
그런데 여기서 이 늘어나면, 확률 밀도가 위 분포에서 independent random variable를 추출해서 더하는 것이 되기 때문에, 중심 극한 정리에 의해 gaussian distribution이 된다. (이 논문에서는 모든 실험에 , 를 사용했다고 한다.)
그리고 그 를 sinusoidal function에 넣어주면 은 variance 0.5의 arcsine 분포로 근사된다. (그림에서 After RFF)
이제 Bacon 논문을 따라 아래와 같이 initialize하면
가 늘어남에 따라 은 standard normal distribution에 근사하고, 최종 elementwise multiplication은 arcsine 분포와 standard normal 분포의 product이다.
그렇게 계속해서 linear layer를 지나면서 또 다른 standard normal distribution을 얻게 된다.
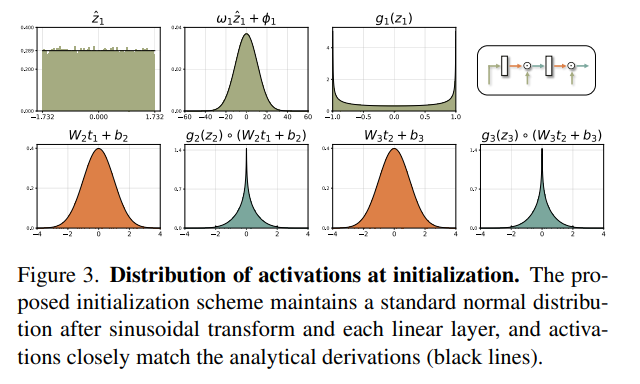
Linear transformation을 통과한 arcsine distribution의 random variable이 gaussian distribution을 가지게 되는 것이 살짝 이해가 잘 안간다. 베이컨 논문을 나중에 공부해야 잘 이해하려나
Spectrum Coverage and Inductive Bias
INR의 관점에서 inductive bias는 주로 spectrum coverage에 관련되어있다.
FFN과 같은 pure mlp 방법들은 어떤 frequency mapping 를 통해 아래 함수의 frequency support를 결정하는 등의 방법을 사용하여, target signal의 spectrum을 cover하고자 하였다.
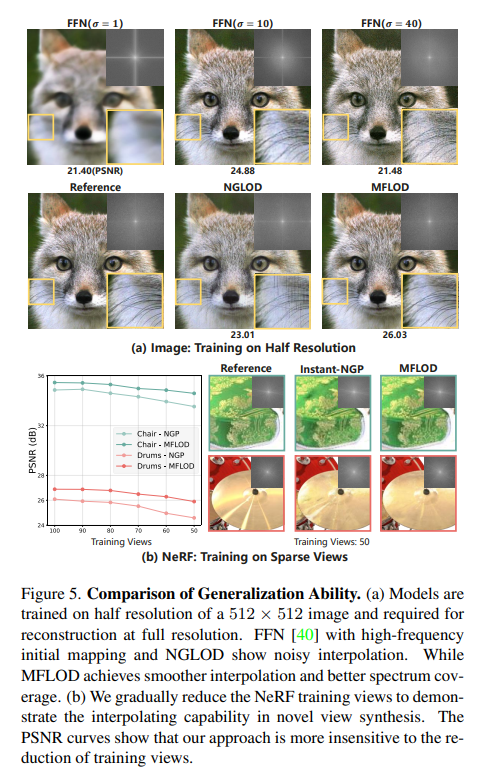
하지만 결론적으로 low frequency initial mapping 는 underfitting을 야기할 것이고, high-frequency initial mapping은 over-fitting과 noisy interpolation을 야기할 것이다.
예를 들어, target signal의 spike를 matching하기 위해서는 위 식에서 high-frequency 성분에 큰 weight를 주어야할 것이고 결과적으로 aliased reconstruction결과를 얻게 될 것이다. (periodicity of Fourier bases)
반면에 Instant-NGP같은 feature volume 방법들은 사실 spectrum의 관점에서 이해하기는 어렵지만, 직관적으로 fine level에서 local signal에 overfitting되는 단점을 가지고 있다고 볼 수 있다.
NTK for Generalization Analysis
MFLOD가 generalization 측면에서 우수한 이유를 설명하기 위해 이 논문에서는 neural tangent kernel (NTK)를 도입했다. 아래 논문에서 잘 설명되어 있는 것 같다. (나는 이해 잘 못했다.)
Fourier Features Let Networks Learn High Frequency Functions in Low Dimensional Domains (Matthew Tancik, Pratul P. Srinivasan, Ben Mildenhall, Sara Fridovich-Keil, Nithin Raghavan, Utkarsh Singhal, Ravi Ramamoorthi, Jonathan T. Barron, Ren Ng / Neurips 2020)
간단하게 설명하자면, NTK는 neural network의 학습 과정이 neural tangent kernel ()을 사용한 kernel regression과 같다는 데서 나온 개념으로,
이 내적인 어떤 kernel trick function 을 정의하면 내 모델의 예측 값 의 trajectory를 아래와 같이 표현할 수 있다.
이때, 로 정의하고 미분 방정식을 풀어주면, (일 때, training loss가 0으로 수렴하는 것도 볼 수 있다.)
Kernel 는 대부분의 overparameter case에서 positive definite 행렬이므로, 아래와 같이 표현할 수 있다. (eigenvalue decomposition하고, eigenvector의 matrix가 orthogonal하므로 )
이때, 가 rate of convergence로 해당 eigenvector 방향으로 얼마나 빠르게 수렴하는지를 나타내준다.
즉, eigenvalue가 큰 쪽으로는 빠르게 수렴하고, 작은 쪽으로는 느리게 수렴하게 된다.
보통 이미지 상에서는 eigenvalue가 큰 쪽이 바로 low frequency 영역이기 때문에, low frequency를 더 잘 배우고, high frequency를 못 배우는 것이다.
이 논문에서는 아래 그림에서 NTK의 eigenfunction이 서로 high-frequency를 가질수록 overfitting tendency를 증명하는 것이라고 한다. (의미를 연결시키는게 잘 안된다.)

Experiments and Results
이 논문에서는 3D shape representation, image fitting, novel view synthesis를 통해 MFLOD를 검증하였고, 아래의 장점을 부각시켰다.
1) Fast training & evaluation,
2) Superior quality
3) Frequency control
4) Less tendency to overfit
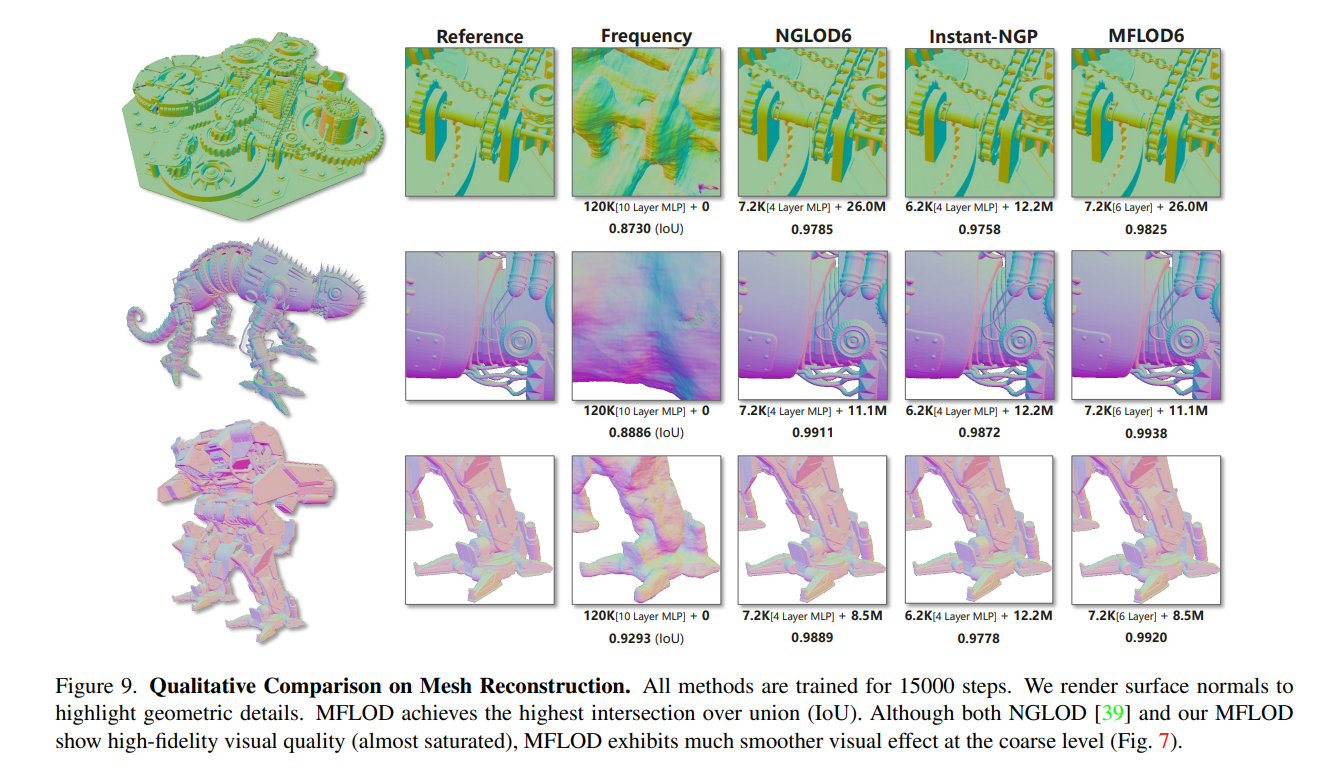
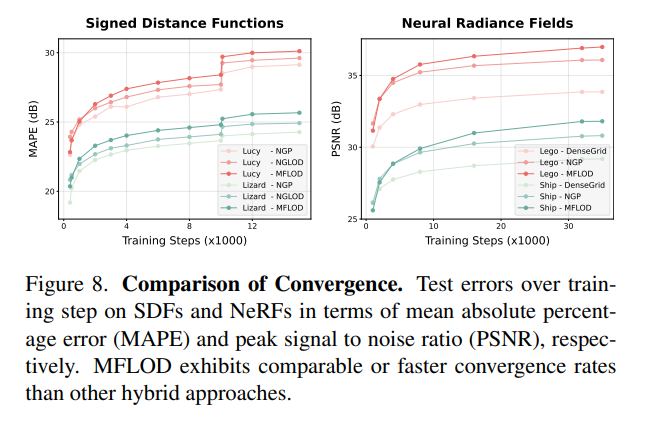
아래는 NeRF에서의 convergence rate와 qualitative result이다.

Discussion
공부할 내용이 많고, 좋은 분석을 한 논문.
논문의 내용을 다 담지는 못해서 아쉽지만 나중에 더 공부해서 정리할 예정
code release가 아직 안됬는데, 코드 보면 더 이해가 쉬울 것 같음