1) 모형 학습 목표 및 손실 함수 설정
t = 1 , . . . , T t=1,...,T t = 1 , . . . , T w t w_t w t m m m
L i k e l i h o o d = L ( θ ) = ∏ t = 1 T ∏ − m ≤ j ≤ m j ≠ 0 P ( w t + j ∣ w t ; θ ) Likelihood = L(\theta)= \prod\limits_{t=1}^{T}\prod\limits_{\substack{-m \leq j \leq m \\ j \neq 0}}P(w_{t+j}|w_t;\theta) L i k e l i h o o d = L ( θ ) = t = 1 ∏ T − m ≤ j ≤ m j = 0 ∏ P ( w t + j ∣ w t ; θ )
목표 함수 또는 손실 함수는 (average) negative log likelihood이다. 이는 조건부 최대가능도 추정법(conditional maximum likelihood estimation)을 따르는 교차 엔트로피 손실 함수(cross entropy loss function)의 하나이다.곱셈 대신 덧셈이 쉬우므로 로그 계산을 도입하고, 예측 정확도를 최대화하는 것은 손실 함수를 최소화하는 것과 같으므로 음수로 변환한다.
J ( θ ) = − 1 T log L ( θ ) = − 1 T ∑ t = 1 T ∑ − m ≤ j ≤ m j ≠ 0 log P ( w t + j ∣ w t ; θ ) J(\theta)=-\dfrac{1}{T}\log L(\theta)=-\dfrac{1}{T} \sum\limits_{t=1}^T \sum\limits_{\substack{-m \leq j \leq m \\ j \neq 0}} \log P(w_{t+j}|w_t;\theta) J ( θ ) = − T 1 log L ( θ ) = − T 1 t = 1 ∑ T − m ≤ j ≤ m j = 0 ∑ log P ( w t + j ∣ w t ; θ )
P ( w t + j ∣ w t ; θ ) P(w_{t+j}|w_t;\theta) P ( w t + j ∣ w t ; θ ) w w w c c c v w v_w v w o o o u w u_w u w
P ( w t + j ∣ w t ; θ ) = P ( o ∣ c ) = exp ( u o T v c ) ∑ w ∈ V exp ( u w T v c ) P(w_{t+j}|w_t;\theta) = P(o|c) = \dfrac{\exp(u_o^Tv_c)}{\sum\limits_{w \in V} \exp(u_w^Tv_c)} P ( w t + j ∣ w t ; θ ) = P ( o ∣ c ) = w ∈ V ∑ exp ( u w T v c ) exp ( u o T v c )
유사도를 계산하는 방법은 내적이다. 단어 벡터의 내적값이 커질수록 확률이 더 커진다는 의미가 있다.
내적값이 음이어도 이를 양으로 변환할 수 있도록 지수 함수를 취한다.
모든 단어에 대해 정규화하여 확률 분포를 만들어낸다.
이는 소프트맥스(softmax) 함수의 예시이기도 하다. 소프트맥스 함수는 임의의 실수값을 확률 분포 ( 0 , 1 ) (0,1) ( 0 , 1 )
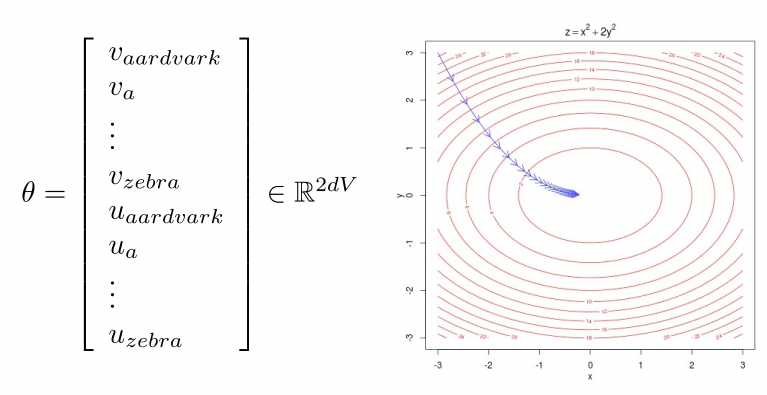
Word2Vec 모델을 훈련한다는 것은 손실 함수를 최소화하기 위해 매개변수를 조정하는 것을 의미한다. 단어 벡터가 d d d 2 V 2V 2 V d × 2 V d \times2V d × 2 V
2) 각 매개변수에 대해 편미분하여 gradient 계산
손실 함수 최소화
J ( θ ) = − 1 T log L ( θ ) = − 1 T ∑ t = 1 T ∑ − m ≤ j ≤ m j ≠ 0 log P ( w t + j ∣ w t ; θ ) J(\theta)=-\dfrac{1}{T}\log L(\theta)=-\dfrac{1}{T} \sum\limits_{t=1}^T \sum\limits_{\substack{-m \leq j \leq m \\ j \neq 0}} \log P(w_{t+j}|w_t;\theta) J ( θ ) = − T 1 log L ( θ ) = − T 1 t = 1 ∑ T − m ≤ j ≤ m j = 0 ∑ log P ( w t + j ∣ w t ; θ )
P ( w t + j ∣ w t ; θ ) = P ( o ∣ c ) = exp ( u o T v c ) ∑ w ∈ V exp ( u w T v c ) P(w_{t+j}|w_t;\theta) = P(o|c) = \dfrac{\exp(u_o^Tv_c)}{\sum\limits_{w \in V} \exp(u_w^Tv_c)} P ( w t + j ∣ w t ; θ ) = P ( o ∣ c ) = w ∈ V ∑ exp ( u w T v c ) exp ( u o T v c ) v c v_c v c
∂ ∂ v c log P ( o ∣ c ) = ∂ ∂ v c log exp ( u o T v c ) ∑ w ∈ V exp ( u w T v c ) = ∂ ∂ v c log exp ( u o T v c ) ⏟ (1) − ∂ ∂ v c log ∑ w ∈ V exp ( u w T v c ) ⏟ ( 2 ) \dfrac{\partial}{\partial{v_c}} \log P(o|c) = \dfrac{\partial}{\partial{v_c}} \log \dfrac{\exp(u_o^Tv_c)}{\sum\limits_{w \in V} \exp(u_w^Tv_c)} = \underbrace{\dfrac{\partial}{\partial{v_c}} \log \exp(u_o^Tv_c)}_{\text{(1)}} - \underbrace{\dfrac{\partial}{\partial{v_c}} \log \sum\limits_{w \in V} \exp(u_w^Tv_c)}_{\text{}(2)} ∂ v c ∂ log P ( o ∣ c ) = ∂ v c ∂ log w ∈ V ∑ exp ( u w T v c ) exp ( u o T v c ) = (1) ∂ v c ∂ log exp ( u o T v c ) − ( 2 ) ∂ v c ∂ log w ∈ V ∑ exp ( u w T v c )
(1) ∂ ∂ v c log exp ( u o T v c ) = ∂ ∂ v c u o T v c = u o \text{(1)} \space \dfrac{\partial}{\partial{v_c}} \log \exp(u_o^Tv_c) = \dfrac{\partial}{\partial{v_c}} u_o^Tv_c = u_o (1) ∂ v c ∂ log exp ( u o T v c ) = ∂ v c ∂ u o T v c = u o
(2) ∂ ∂ v c log ∑ w ∈ V exp ( u w T v c ) = 1 ∑ w ∈ V exp ( u w T v c ) ( ∂ ∂ v c ∑ x ∈ V exp ( u x T v c ) ) = 1 ∑ w ∈ V exp ( u w T v c ) ( ∑ x ∈ V ∂ ∂ v c exp ( u x T v c ) ) = 1 ∑ w ∈ V exp ( u w T v c ) ( ∑ x ∈ V exp ( u x T v c ) ∂ ∂ v c u x T v c ) = 1 ∑ w ∈ V exp ( u w T v c ) ( ∑ x ∈ V exp ( u x T v c ) u x ) \begin{aligned} \text{(2)} \space \dfrac{\partial}{\partial{v_c}} \log \sum\limits_{w \in V} \exp(u_w^Tv_c) &= \dfrac{1}{\sum\limits_{w \in V} \exp(u_w^Tv_c)} \biggl(\dfrac{\partial}{\partial{v_c}}\sum\limits_{x \in V} \exp(u_x^Tv_c) \biggr) \\ &= \dfrac{1}{\sum\limits_{w \in V} \exp(u_w^Tv_c)} \biggl( \sum\limits_{x \in V} \dfrac{\partial}{\partial{v_c}} \exp(u_x^Tv_c) \biggr) \\ &= \dfrac{1}{\sum\limits_{w \in V} \exp(u_w^Tv_c)} \biggl( \sum\limits_{x \in V} \exp(u_x^Tv_c) \dfrac{\partial}{\partial{v_c}} u_x^Tv_c\biggr) &= \dfrac{1}{\sum\limits_{w \in V} \exp(u_w^Tv_c)} \biggl( \sum\limits_{x \in V} \exp(u_x^Tv_c) u_x\biggr) \end{aligned} (2) ∂ v c ∂ log w ∈ V ∑ exp ( u w T v c ) = w ∈ V ∑ exp ( u w T v c ) 1 ( ∂ v c ∂ x ∈ V ∑ exp ( u x T v c ) ) = w ∈ V ∑ exp ( u w T v c ) 1 ( x ∈ V ∑ ∂ v c ∂ exp ( u x T v c ) ) = w ∈ V ∑ exp ( u w T v c ) 1 ( x ∈ V ∑ exp ( u x T v c ) ∂ v c ∂ u x T v c ) = w ∈ V ∑ exp ( u w T v c ) 1 ( x ∈ V ∑ exp ( u x T v c ) u x )
∂ ∂ v c log P ( o ∣ c ) = u o − 1 ∑ w ∈ V exp ( u w T v c ) ( ∑ x ∈ V exp ( u x T v c ) u x ) = u o − ∑ x ∈ V exp ( u x T v c ) ∑ w ∈ V exp ( u w T v c ) u x = u o − ∑ x ∈ V P ( x ∣ c ) u x = o b s e r v e d − e x p e c t e d \dfrac{\partial}{\partial{v_c}} \log P(o|c) = u_o - \dfrac{1}{\sum\limits_{w \in V} \exp(u_w^Tv_c)} \biggl( \sum\limits_{x \in V} \exp(u_x^Tv_c) u_x\biggr) = u_o - \sum\limits_{x \in V} \dfrac{\exp(u_x^Tv_c)}{\sum\limits_{w \in V} \exp(u_w^Tv_c)} u_x = u_o - \sum\limits_{x \in V} P(x|c)u_x = observed - expected ∂ v c ∂ log P ( o ∣ c ) = u o − w ∈ V ∑ exp ( u w T v c ) 1 ( x ∈ V ∑ exp ( u x T v c ) u x ) = u o − x ∈ V ∑ w ∈ V ∑ exp ( u w T v c ) exp ( u x T v c ) u x = u o − x ∈ V ∑ P ( x ∣ c ) u x = o b s e r v e d − e x p e c t e d
∂ ∂ u w \dfrac{\partial}{\partial{u_w}} ∂ u w ∂
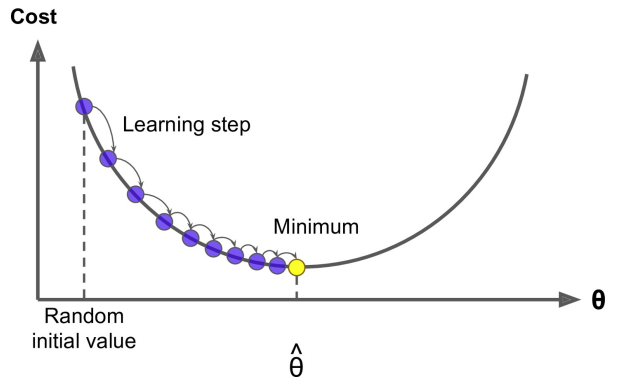
3) 경사 하강법 적용하여 손실 함수의 최솟값 계산
교차 엔트로피 함수의 경우 convexity가 보장되기 때문에 최솟값을 구할 수 있다.경사 하강법(Gradient Descent) 에서는 J ( θ ) J(\theta) J ( θ ) θ \theta θ J ( θ ) J(\theta) J ( θ )
θ n e w = θ o l d − α ∇ θ J ( θ ) \theta^{new} = \theta^{old} - \alpha \nabla_\theta J(\theta) θ n e w = θ o l d − α ∇ θ J ( θ )
while True:
theta_grad = evaluate_gradient(J, corpus, theta)
theta = theta - alpha * theta_grad
α = \alpha= α =
그런데 J ( θ ) J(\theta) J ( θ ) ∇ θ J ( θ ) \nabla_\theta J(\theta) ∇ θ J ( θ ) 확률적 경사 하강법(Stochastic gradient descent) 을 사용하는 것이 일반적이다.
while True:
window = sample_window(corpus)
theta_grad = evaluate_gradient(J, window, theta)
theta = theta - alpha * theta_grad