How to do Breusch-Pegan Test

BP test는 BF test에서 잡아낼 수 없는 것을 잡아준다.
예를 들자면, BF에서는 2개의 그룹으로 나누어 등분산성을 검정했다. 하지만 2개의 그룹의 variability는 같으나 각각의 그룹에서 또 그룹을 나눠서 생각해보면 등분산성이 깨질 수 있다. 그래서 그 대안으로 BP test를 할 수 있다.
BP test로는 다음과 같이 수행하면 된다.

위의 식에서 만약 $\mathit{\gamma}_1$이 0이 아니라면 등분산성이 깨지는 것이다.

test를 위해 SSE와 SSR값을 구하고, 가설을 다음과 같이 세운다.

$H_0 : \mathit{\gamma}_1 = 0$
$H_1 : \mathit{\gamma}_1 \not =0$

검정통계량은 다음과 같다.
$X_{BP}^2 = {{SSR^* \over 2} / ({SSE \over 2})^2}$
(귀무가설이 맞다면 검정통계량은 카이제곱분포를 따른다)

F test for Lack of Fit

lack of fit test는 항상 쓸 수 있는 test가 아니다.
반드시 특정 값들이 $X_i$에 대해 여러번 반복되어야 한다. 즉 plot 그림에서 특정 x에 대한 값이 2개 이상 나와야 한다.

그렇다면 우리는 $E(Y_i|X_i) = \bar{Y}_i$를 계산할 수 있고, 이 $\bar{Y}_i$들이 line으로 표현이 된다면 또 다시 $\mathit{\beta}_0+\mathit{\beta}_iX_i$ 로 표현할 수 있다. (simple linear regression이 된다)

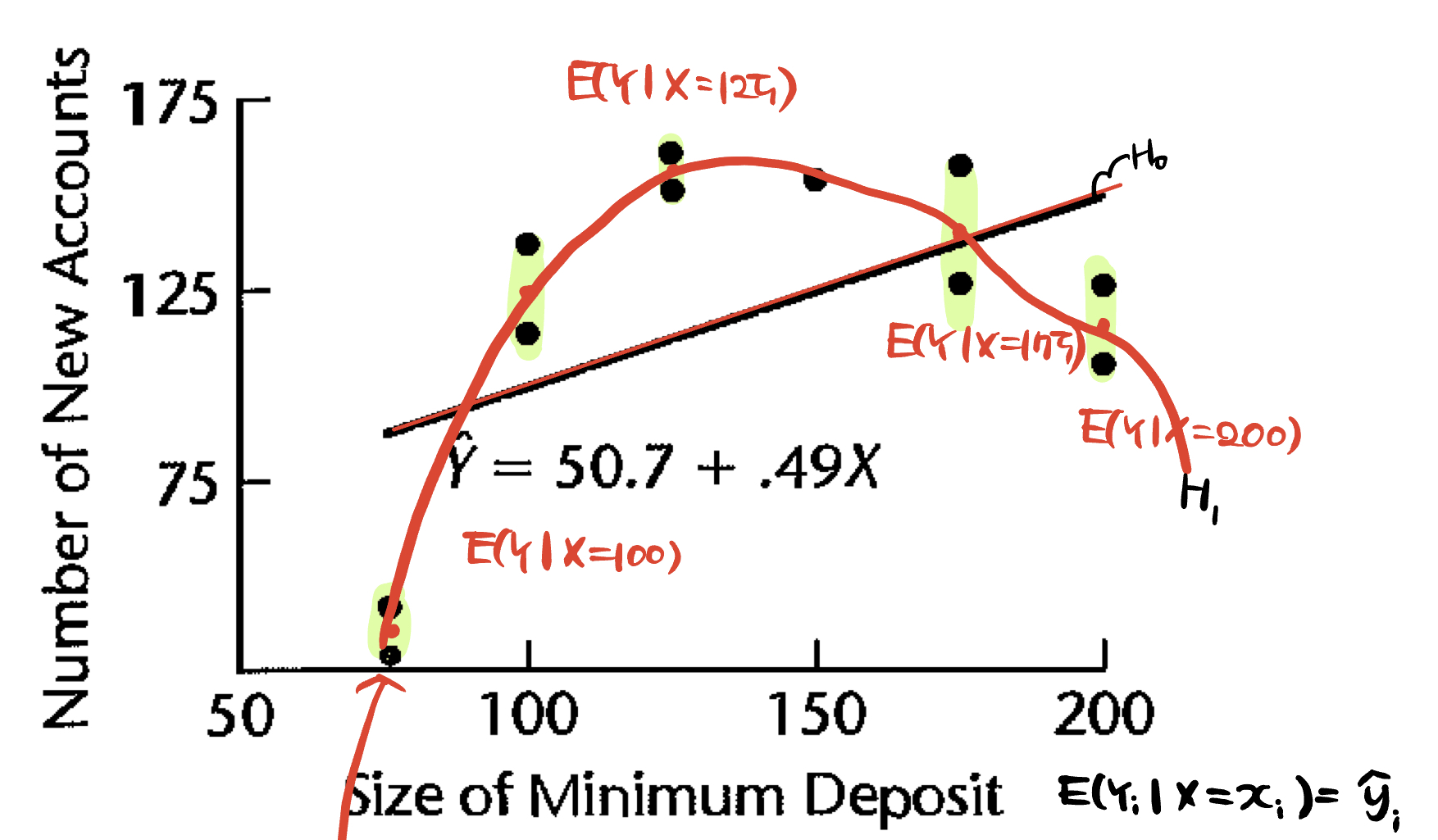
위와 같은 그림에서 확인해보면 각 $X$당 $Y$값이 여러개 있음을 보이고 있다.
가설을 다음과 같이 세워볼 수 있다.

$H_0 : E(Y_{ij}|X_{ij}) = \mathit{\beta}_0+\mathit{\beta}_1X_i$
$H_1 : E(Y_{ij}|X_{ij}) = \mathit{\mu}_i$

귀무가설은 Full model, 대립가설은 reduced model임을 확인할 수 있다. (앞의 포스팅 GLT를 참고하면 된다)

simple linear regression을 구하고, SSE와 자유도를 구하므로써 검정통계량을 구할 수 있다. 이 값들이 $SSE(R), df_R$이 된다.

$SSE(F) = \sum{\sum{(Y_{ij}-\bar{Y}_i)^2}}$
$df_F = n-c$ (여기서 c는 distinct한 $x$의 값이 된다.)
$SSE(F)$는 pure error라고도 불린다!

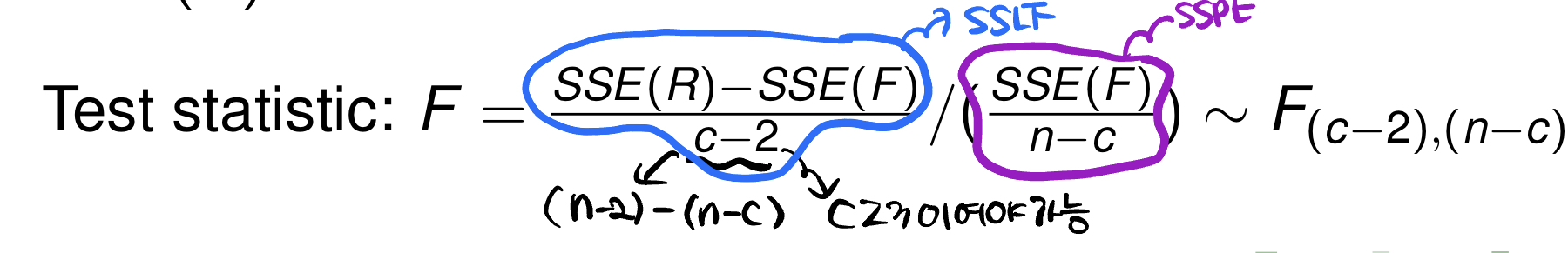
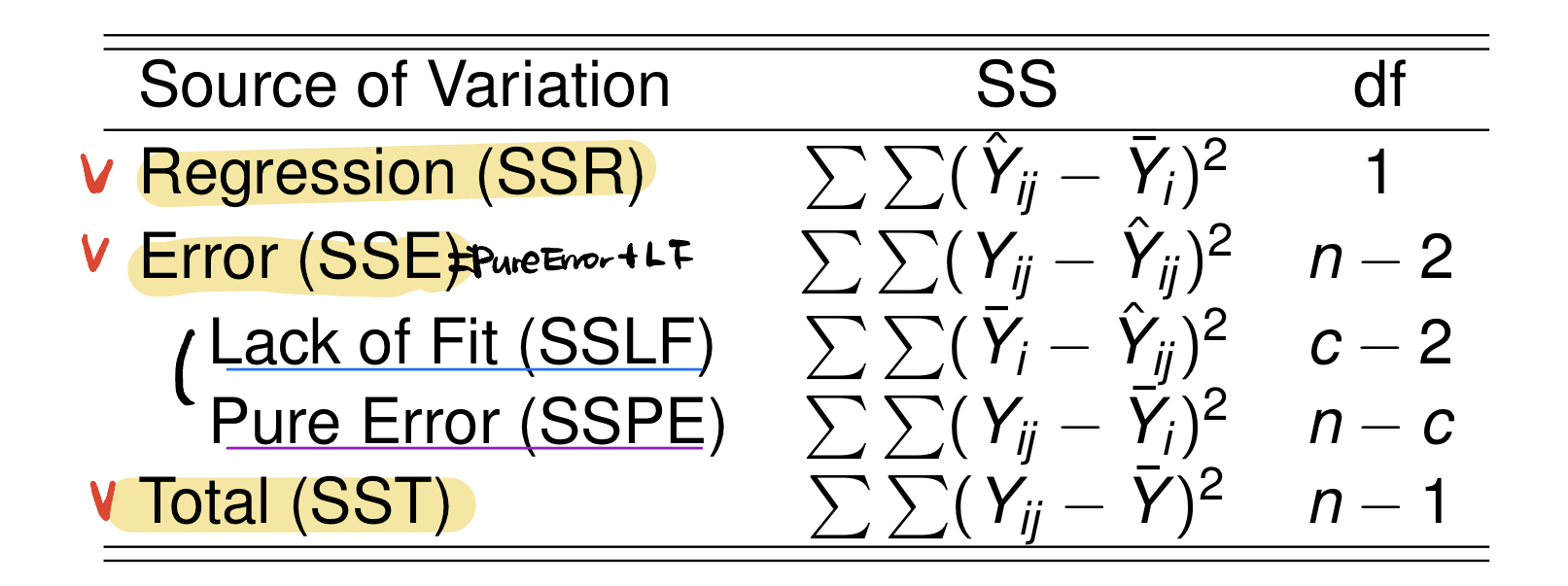
Anova Table for lack of fit

이것은 새로운 것은 아니지만 GLT에 관련한 것이다.

Transformations

도저히 구제가 안될 것 같은 상황에서는 '변환'을 써먹을 수 있다!

X transformation 예시는 아래와 같다.

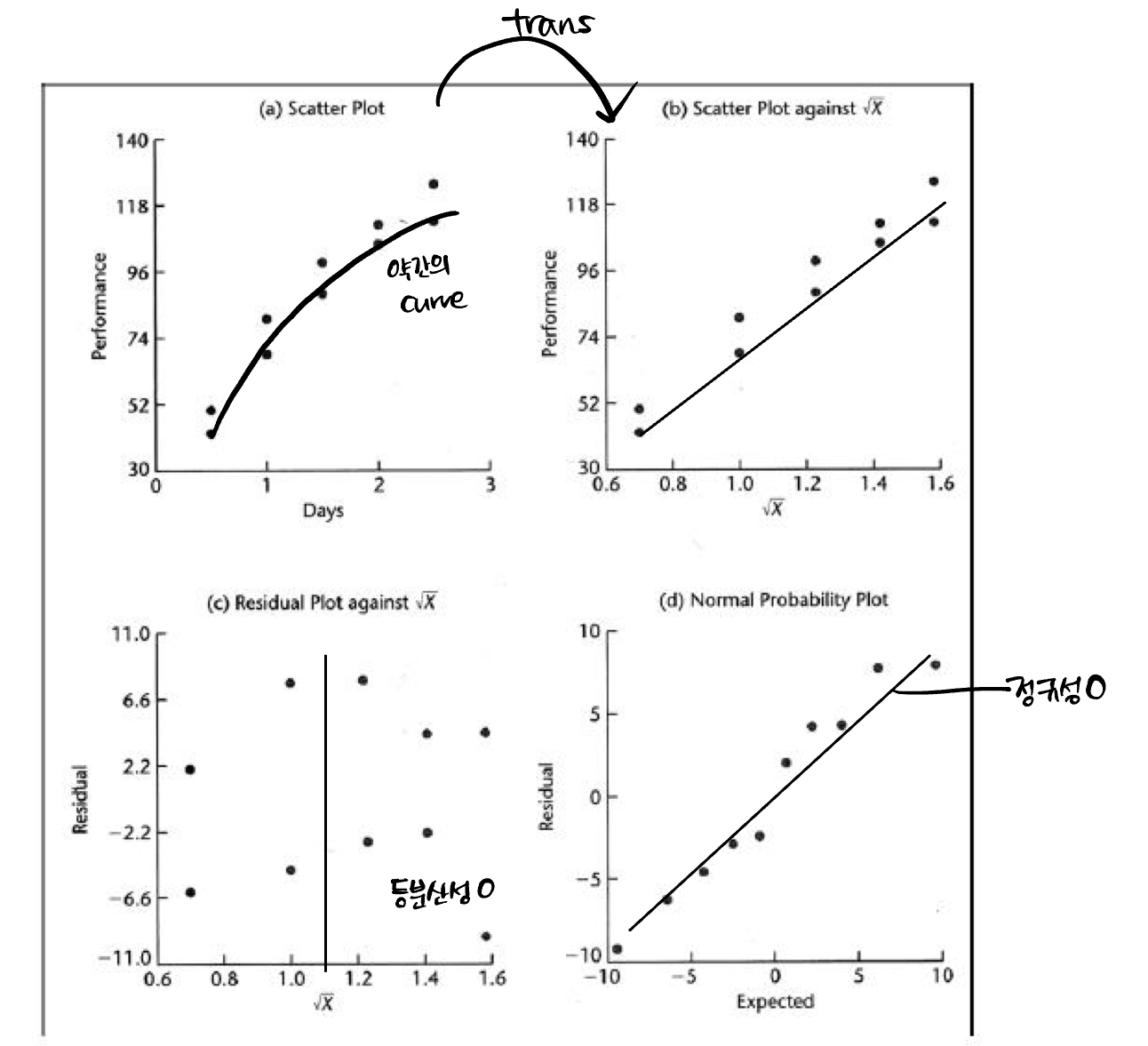
(a)번의 scatter plot을 보면 약간의 curve형태를 띄는 것을 볼 수 있다. 우리는 이것을 $\sqrt{X}$로 변환을 해주면 (b)와 같이 조금 평평해진 모습을 볼 수 있고, residual plot을 통해 정규성과 등분산성까지 확인할 수 있다.

만약 정규성과 등분산성이 깨졌다면, $Y$를 transformation 한다!
완화가 될 수도 있지만 물론 해결이 안될 수도 있다.

---

to be continued