이전 포스트를 참고하면, $X$를 transform하는 상황과 $Y$를 transform 하는 상황까지 작성을 했다!

특히 어떤 상황에서 $Y$를 transform 해야하는지 생각해보면, '정규성'이 깨졌을 때 그리고 '등분산성'이 깨졌을때 $Y$ transformation을 시도해보는 것이다.

방법은 다양하다.

• $logY$
• $\sqrt{Y}$
• ${1 \over Y}$

와 같이 transformation을 시도해보는 것이다.

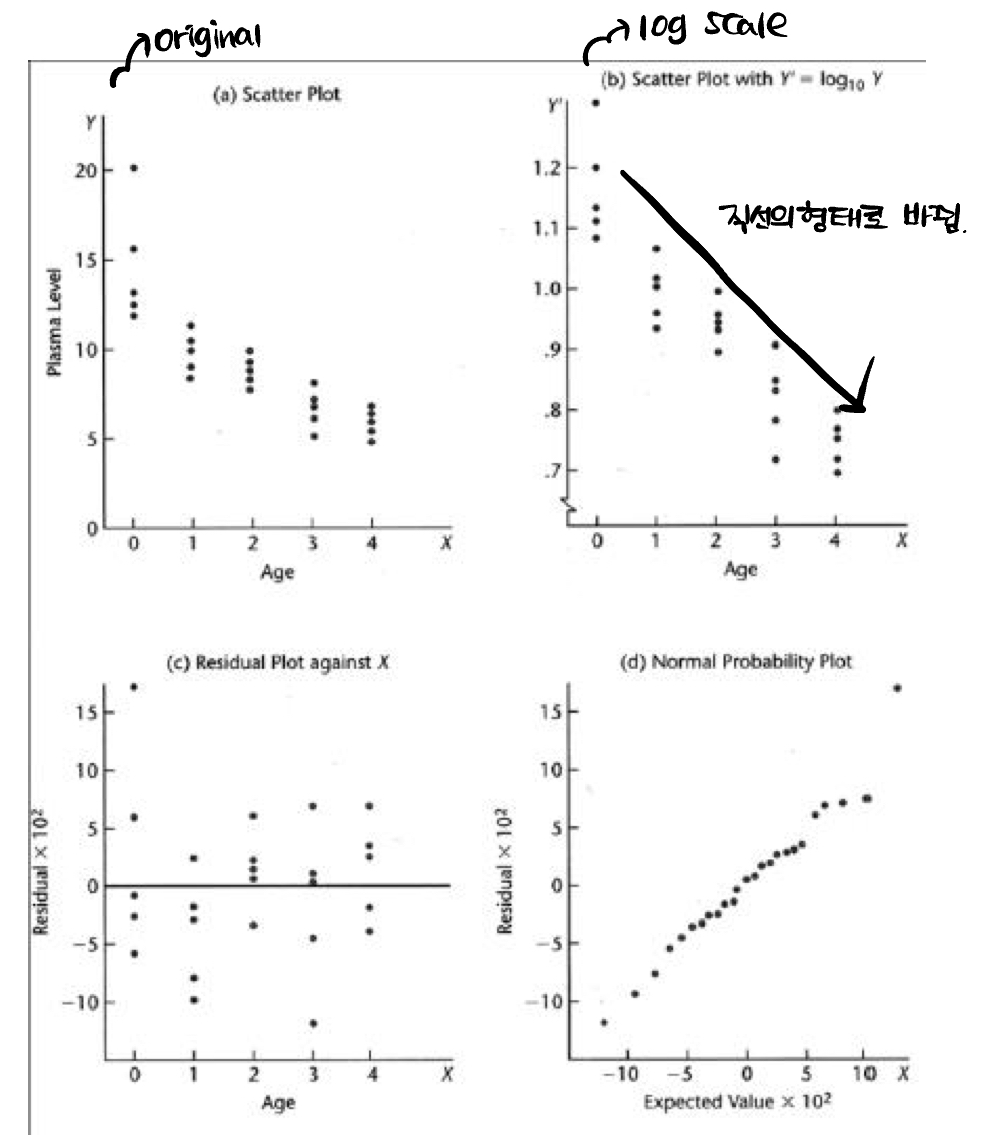
이것이 그 예시다.
(a) Plot은 original plot, (b) plot은 $logY$로의 transformation이 일어난 plot이다. original에 비교하면 그래프가 직선의 형태로 변화한 것을 확인할 수 있다. (심지어 육안으로 보기 가능)

Box-Cox transformation

위의 예시는 육안으로도 log scale이 도움이 되었다는 것을 판단할 수 있다.
하지만 일반적인 경우에서는 그림만 보고 판단하기가 매우 어렵다.
그래서 transformation form을 power로 표현하는 것이다.

위의 식이 기본 형태이다. $\mathit{\lambda}$를 조절해가며 적당한 값을 찾는 것이 Box-cox 되시겠다.

Box-cox trans, find good lambda

그렇다면 $Y_i^{\mathit{\lambda}} = \mathit{\beta}_0 + \mathit{\beta}_1X_i+\mathit{\epsilon}_i$ 를 생각해보자.
우리는 각 모수들을 SSE를 최소화하는 방법으로 찾아야한다.

하지만...
$\mathit{\lambda}$를 찾아서 값을 계산하는 것은 매우 쉬운일이 아니다...
그래서 box-cox 변환은 결국 '$\mathit{\lambda}$ 정하기 게임'이라고 생각하면 편하다.

그래서 무수히 많은 $\mathit{\lambda}$를 다 계산한 뒤 나열한다. 그리고 그 중 SSE가 가장 적은 것을 찾는다.
그리고 그 중 가장 'reasonable'한 값으로 골라주는 것이다.

왜 reasonable 이라는 단어를 사용했는지에 대해 조금 생각해볼 필요가 있다. 다음 예시를 살펴보며 생각해보자!

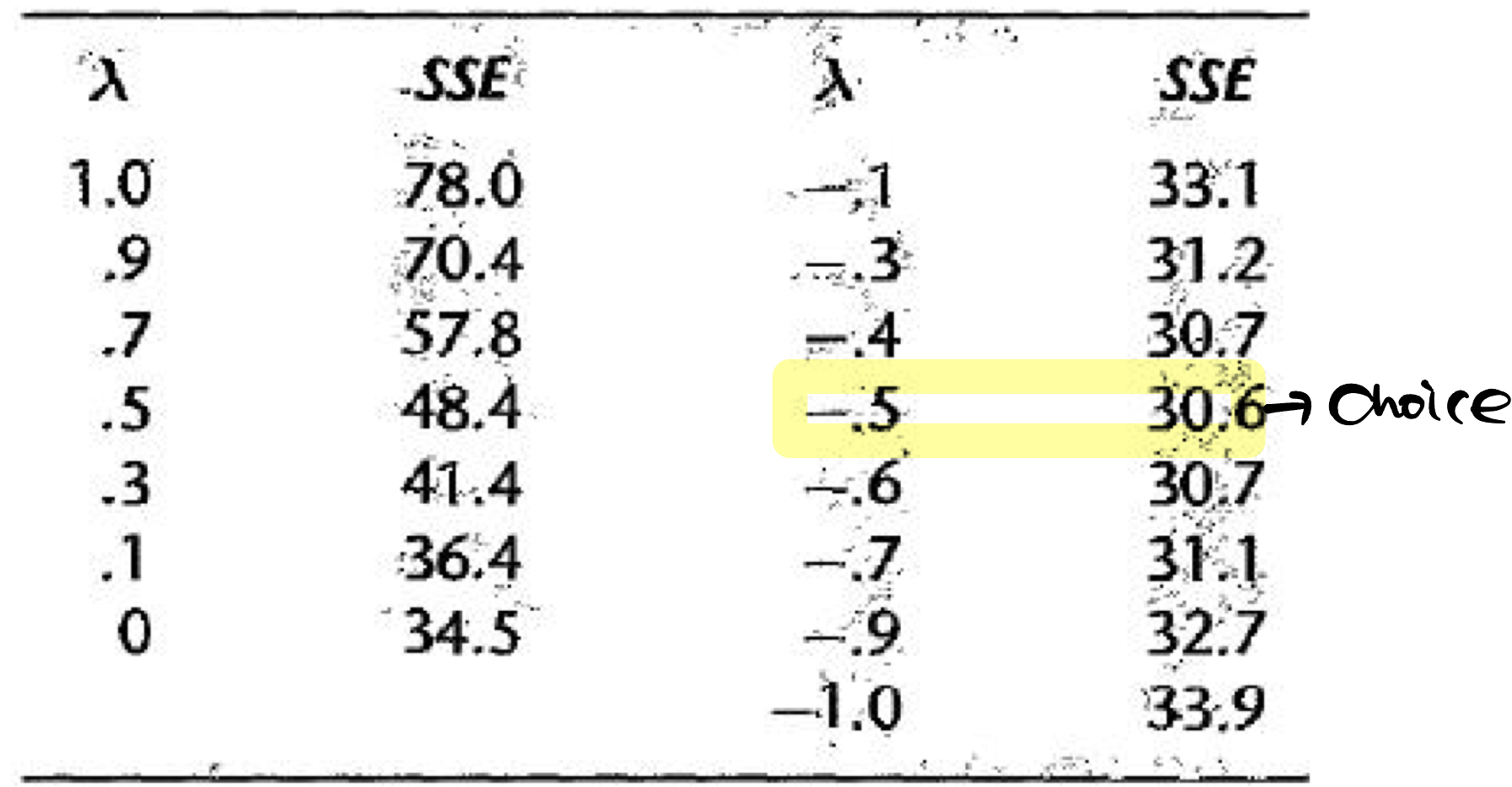
이 예시에서는 SSE가 최소인 -0.5를 선택하면 된다.
하지만 다른 예시를 생각해보자.

SSE를 최소화 하는 $\mathit{\lambda}$가 0.375였고, 그 다음이 0.5였다고 가정해보자. 우리는 $Y^{0.375}$가 나타내는 의미를 이해하지 못한다. (common sense에서 생각하면..) 그렇지만 $Y^{0.5}$가 나타내는 의미는 잘 알고 있다. 그러면 이 상황에서는 0.5를 $\mathit{\lambda}$로 택하는 것이 reasonable하다는 것이다.

그래서 결론은,

"최소의 $\mathit{\lambda}$를 찾는 것이 아닌 최적의 $\mathit{\lambda}$를 찾자!"로 바뀌는 것이다.

이것이 왜 'reasonable'이라는 단어를 썼는지에 대한 이유이다.

<정리>
1. 선형성이 깨졌을 때는 $X$를 transform 한다.
2. 등분산성이나 정규성이 깨졌을 때는 $Y$를 transform.

R에서 Box-cox 이용하고 power transform 이용해보기

### get data

ta01 <- read.table("CH01TA01.txt")
names(ta01)<-c("X","Y")


### data ordering

ord <- order(ta01$X)
ta01 <- ta01[ord,]
attach(ta01)


### lm fit

lm.ta01 <- lm(Y~X, data = ta01)
resid <- lm.ta01$resid
resid
##          14           2          17          21          11          23 
## -20.7698990 -48.4719192  42.5280808 103.5280808 -45.1739394  38.8260606 
##           3          10          18           6           5          12 
## -19.8759596 -83.8759596  27.1240404 -52.5779798  48.7200000 -60.2800000 
##          25           1           8          24           4          13 
##  10.7200000  51.0179798   4.0179798  -5.9820202  -7.6840404   5.3159596 
##          19          22           9          16          15          20 
##  -6.6840404  84.3159596 -66.3860606   0.6139394 -20.0880808 -34.0880808 
##           7 
##  55.2098990
### draw plot

plot(resid)

위와 같이 데이터를 불러와주고, lm함수를 fit한 뒤 ploting을 해준다.

하지만 뭐다? 우리는 한눈에 보는 것이 좋으므로 2by2 모양의 Plotting을 해준다. 코드는 아래와 같다.

ta01.lm <- lm(Y~X, data = ta01)
par(mfrow = c(2,2))
plot(ta01$X, ta01.lm$resid, xlab = "X", ylab="residuals")
plot(ta01.lm$fitted , ta01.lm$resid, xlab="fitted value", ylab="residuals")
qqnorm(ta01.lm$resid)
qqline(ta01.lm$resid)
plot(ta01.lm$resid)

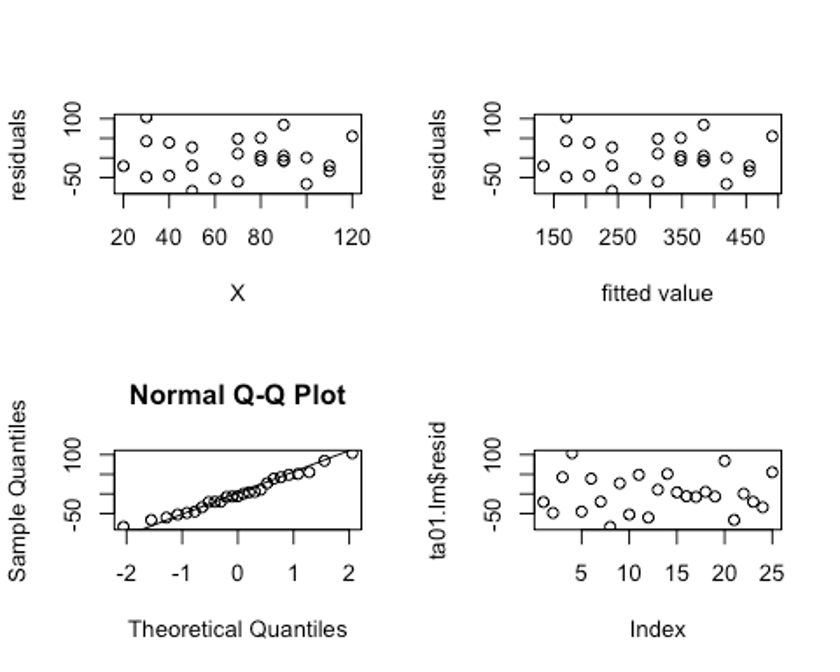
짜자잔! 한눈에 확인할 수 있는 plot 완성이다.

Box-Cox를 이용하려면, car 패키지가 필요하다.
다음과 같이 코드를 써준다.

install.packages('car')
library(car)

##### best lambda
powerTransform(ta08.lm)
## Estimated transformation parameter 
##          Y1 
## -0.06754728
p1 <- powerTransform(ta08.lm)
summary(p1)
## bcPower Transformation to Normality 
##    Est Power Rounded Pwr Wald Lwr Bnd Wald Upr Bnd
## Y1   -0.0675           1      -1.3108       1.1757
## 
## Likelihood ratio test that transformation parameter is equal to 0
##  (log transformation)
##                              LRT df    pval
## LR test, lambda = (0) 0.01136794  1 0.91509
## 
## Likelihood ratio test that no transformation is needed
##                            LRT df     pval
## LR test, lambda = (1) 2.842603  1 0.091795
boxCox(ta08.lm)

####### choose lambda (-1.xx, 1.xx) 

ta08.lm2 <- lm(Y~X, data=ta08)
par(mfrow=c(2,2))

powerTransform() 함수를 이용하고 결과 값을 변수에 넣어준 뒤 summary함수를 이용하면 나의 best power를 볼 수 있다.
또, boxCox() 함수를 이용하면 다음과 같은 그림을 화면에 띄워준다.

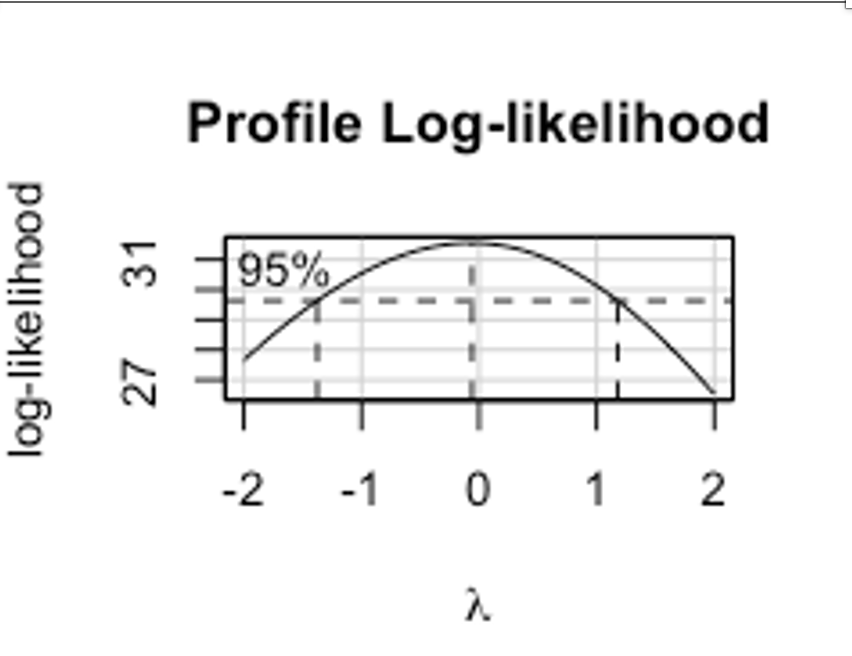
95%라 적혀있고, 그 값에 해당하는 각 $X$값 범위에 있는 $\mathit{\lambda}$를 선택하는 것이 좋다는 의미이다.

이렇게 transformation과 test에 대해 총 3번의 포스팅으로 정리했다!
다음 포스트부터는 회귀분석을 위한 Matrix에 대해 공부해볼 것이다.