2. 지도학습

지도학습은 입력과 출력 샘플 데이터가 존재, 주어진 입력으로부터 출력을 예측하고자 할 때 사용

2.1 분류와 회귀

• 분류(Classification): 미리 정의된, 가능성 있는 여러 클래스 레이블(class label) 중 하나를 예측하는 것
  -> 이진 분류(binary classification) or 다중 분류(multiclass classification)
• 회귀(regression): 연속적인 숫자(실수,부동소수점수)를 예측
  -> 출력값에 연속성이 존재

2.2 일반화, 과대적합, 과소적합

• 일반화(generalization): 모델이 처음 보는 데이터에 대해 정확하게 예측 = “훈련 세트에서 테스트 세트로 일반화(generalization)되었다”

• 알고리즘이 잘 작동하는지 확인 = 테스트 세트로 평가

• 과대적합(overfitting): 가진 정보를 모두 사용해서 너무 복잡한 모델을 만드는 것 -> 새로운 데이터에 일반화 어려움

• 과소적합(underfitting): 너무 간단한 모델이 선택되어 데이터의 면면과 다양성을 잡아내지 못하고 훈련 세트에도 맞지 않음

• 데이터 셋에 다양한 데이터 포인트가 많을수록 과대적합 없이 더 복잡한 모델을 만들 수 있음(같은 데이터 포인트를 중복하거나 매우 비슷한 데이터를 모으는 것은 도움X)

<모델 복잡도에 따른 훈련과 테스트 정확도의 변화>

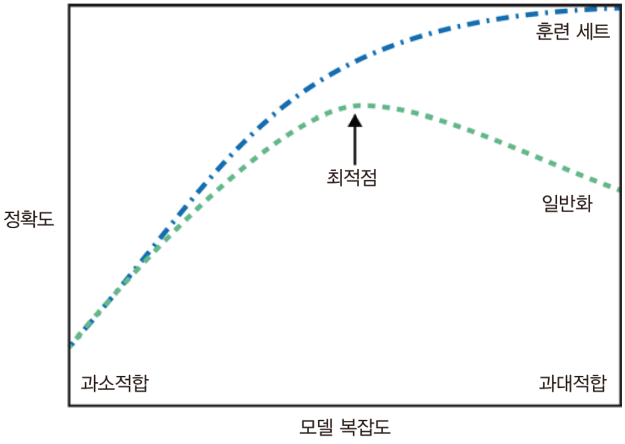
2.3 지도 학습 알고리즘

2.3.1 K-Nearest neighbors

가장 가까운 임의의 k개 이웃 분류 / 회귀

• 장점

  • 매우 쉬운 모델
  • 많이 조정하지 않아도 자주 좋은 성능

• 단점

  • 훈련 세트(특성의 수 or 샘플의 수)가 매우 크면 예측이 느려짐
  • 예측이 느리고 특성 처리 능력 부족 (이런 단점을 커버하는 모델이 선형 모델)

• 분류(Classification)

  • K-Neighbors 분류기
  • 중요한 매개 변수 = 데이터 포인트 사이의 거리를 재는 방법 and 이웃의 수

• 회귀(regression)

  • 회귀: $R^2$(결정계수)= 회귀 모델에서 예측의 적합도를 측정한 것(0 ≤$R^2$≤ 1)
  • n_neighbors 값에 따라 최근접 이웃 회귀로 만들어진 예측 비교

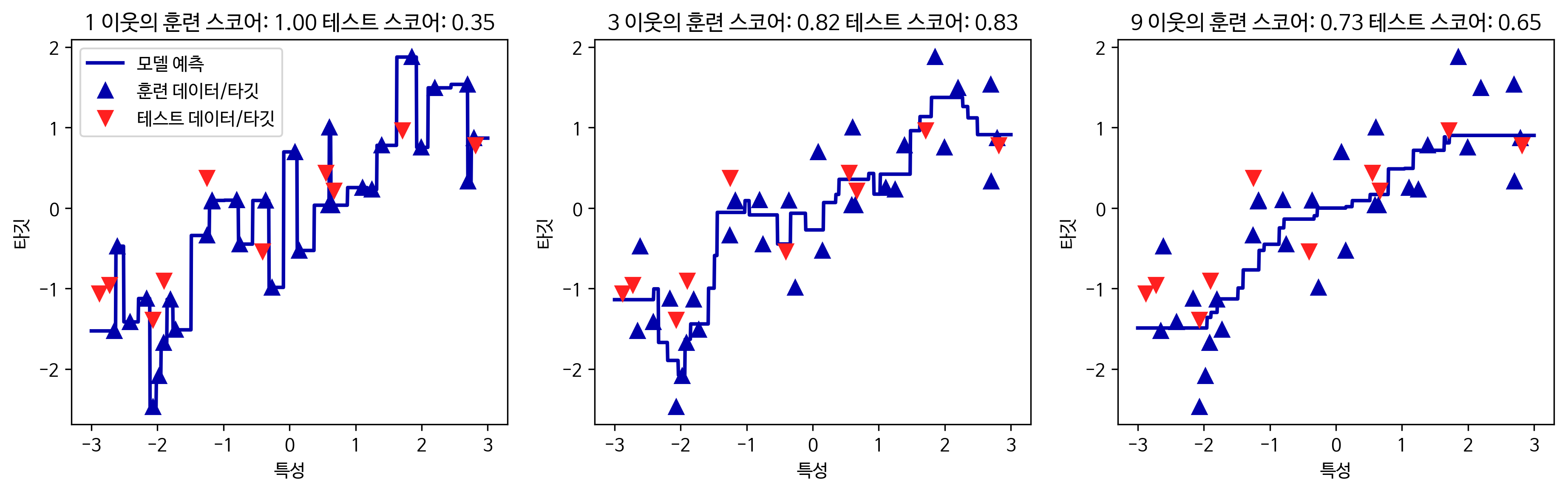
2.3.2 선형 모델

• 입력 특성에 대한 선형함수를 만들어 예측을 수행하는 모델

• 매개변수

  • 회귀모델 = α (클수록 모델이 단순)
  • SVM, Logistc = C (작을수록 모델이 단순)

• L1 regularization

  • 중요한 특성이 많지 않을 때
  • 모델의 해석이 중요한 요소일 때
  • 몇 가지 특성만 사용하도록 해당 모델에 중요한 특성이 무엇이고 효과가 어느정도인지 설명에 용이

• 장점

  • 학습 속도가 빠르고 예측도 빠름
  • 예측이 어떻게 만들어지는지 비교적 쉽게 이해
  • 샘플에 비해 특성이 많을 때 잘 작동, 다른 모델로 학습하기 어려운 매우 큰 데이터셋에 사용

회귀의 선형모델

회귀를 위한 선형 모델은 특성이 하나일 땐 직선, 두 개일땐 평면, 더 높은 차원(특성)에서는 초평면(hyperplane)이 되는 특징을 갖고 있다.

1. 선형 회귀(최소제곱법)

• 선형 회귀(linear regression) or 최소제곱법(OLS, ordinary least squares)

• 예측과 훈련 세트의 타깃 y 사이의 평균제곱오차(mean squared error) 를 최소화하는 파라미터 w와 b를 갖는다.

• 매개변수가 없는 것이 장점 -> 모델의 복잡도를 제어 할 방법이 없음

• 기울기 파라미터(w): 가중치(weight) or 계수(coefficient) -> lr객체의 coef_ 속성에 저장(실수값)

• 편향(offset) or 절편(intercept) 파라미터(b) -> intercept_ 속성에 저장(Numpy 배열)

• 훈련 데이터와 테스트 데이터 사이의 성능 차이는 모델이 과대적합되었다는 것 -> 복잡도를 제어할 수 있는 모델을 사용해야 함.

2. 리지 회귀

• 리지 회귀에서의 가중치(w) 선택은 훈련 데이터를 잘 예측하기 위해서 뿐만 아니라 추가 제약 조건을 만족시키기 위함 = 가중치의 절대값을 최소화(w의 원소가 0에 가깝게) -> 기울기를 작게

• 정규화(regularization): 과대적합이 되지 않도록 모델을 강제로 제한 (리지 회귀에서 사용하는 규제방식 = L2 regularization)

• 모델을 단순하게(계수를 0에 가깝게)하고 훈련 세트에 대한 성능 사이를 절충할 수 있는 방법 제공

• 복잡도를 낮추면 훈련 세트에 대한 성능은 나빠지지만 일반화된 모델이 됨)

• α 매개변수로 훈련 세트의 성능 대비 모델을 얼마나 단순화할지 지정(계수를 얼마나 강하게 0으로 보낼지) - α값이 커진다 = 계수가 작아진다, 모델이 단순화 된다.

• α값이 작아진다 = 계수가 커진다, 모델이 복잡해진다.(너무 낮추면 규제 효과가 없어져 과대적합, LinearRegression과 결과가 비슷해짐)

3. 라쏘 회귀

• 규제 방식 = L1 regularization, 모델에서 제외되는 특성이 생김(계수가 0이 되기도 함)

• 과소적합을 줄이기 위해서 α값을 줄여야함(max_iter(반복 실행 최대 횟수)의 기본값을 늘려야 함)

• 리지 회귀 vs 라소 회귀 : 특성이 많고 그 중 일부만 필요하다면 Lasso, 분석하기 쉬운 모델 Lasso(입력 특성 중 일부만 사용하기 때문), 보통은 리지회귀를 더 선호

• 리지회귀 vs 라쏘회귀

• L1 regularization에서는 몇몇개 가중치가 0이 됨.
• L2 regularization은 가중치를 0으로 만들지는 않지만 0에 매우 가까운 가중치는 모델에 큰 영향을 주지 않음

4. 분류형 선형모델

• 결정 경계가 입력의 선형 함수 = 선형 분류기는 차원에 따라 선, 평면, 초평면을 사용해 두 개의 클래스를 구분

• 선형 모델 학습

  • 특정 계수와 절편의 조합이 훈련 데이터에 얼마나 잘 맞는지 측정
  • 사용할 수 있는 규제가 있는지, 방법은?

• 로지스틱 회귀(Logistic regression) , 서포트 벡터 머신(support vector machine)

• L2 regularization 사용

• 규제의 강도 = 매개변수 C (C의 값이 높아지면 규제 감소, 훈련 세트에 가능한 최대로 맞추려 함 / C값을 낮추면 벡터(w)가 0에 가까워 지도록 함 )

• 알고리즘 C의 값이 낮아지면 데이터 포인트 중 다수에 맞추려 함 / C의 값을 높이면 개개인 포인트를 정확히 분류하려 노력

5. 다중 클래스 분류형 선형 모델

• 일대다 방식: 각 클래스를 다른 모든 클래스와 구분하도록 이진 분류 모델을 학습
• 클래스별 이진 분류기 생성 -> 각 클래스가 계수 벡터(w)와 절편(b)을 하나씩 갖게됨.

2.3.3 나이브 베이즈 분류기

• 각 특성을 개별로 취급해 파라미터를 학습하고 각 특성에서 클래스별 통계를 단순하게 취합

• scikit-learn에 구현된 나이브 베이즈 분류기

  • GaussianNB(연속적 데이터), BernoulliNB(이진 데이터), MultinomialNB(카운트 데이터)
    -> BernoulliNB, MultinomialNB: 텍스트 데이터 분류에 사용
    -> MultinomialNB: 클래스별 특성의 평균 계산 -> GaussianNB: 클래스별 각 특성의 표준편차와 평균 계산

• MultinomialNB, BernoulliNB: α 매개변수 -> α가 주어지면 알고리즘이 모든 특성에 양의 값을 가진 가상의 데이터 포인트를 α개수만큼 추가

• GaussianNB: 대부분 고차원인 데이터셋에 사용

• 훈련과 예측 속도가 빠르며 훈련 과정 이해하기 쉬움 - 희소한 고차원 데이터에서 잘 작동하며 비교적 매개변수에 민감하지 않음

2.3.4 결정트리

분류와 회귀 문제에 널리 사용. 결정에 다다르기 위해 예/아니오 질문을 이어나가며 학습

• 노드: 질문이나 정답을 담은 상자(마지막 노드는 리프(leaf) 라고도 함)

• 결정트리 만들기 - 순수노드(pure node): 타깃 하나로만 이뤄진 리프 노드

• 결정트리의 복잡도 제어

  • 리프노드가 순수노드가 될 때 까지 진행하면 훈련데이터에 과대적합
  • 사전 가지치기(pre-pruning): 트리 생성을 일찍 중단
  • 사후 가지치기(post-pruning) or 가지치기(pruning): 트리를 만든 후 데이터 포인트가 적은 노드를 삭제, 병합

• 결정트리 분석

  • samples: 각 노드에 있는 샘플의 수
  • value: 클래스당 샘플의 수

• 트리의 특성 중요도

  • 특성 중요도(feature importance): 트리를 만드는 결정에 각 특성이 얼마나 중요한지 평가
  • 0과 1사이의 값(0: 전혀 사용하지 않음, 1:완벽하게 타깃 클래스를 예측)
  • 특성 중요도 전체 합 = 1
  • 특성 중요도는 항상 양수, 어떤 클래스를 지지하는지 알 수 없음

• 장단점과 매개변수

  • 모델 복잡도를 조절하는 매개변수는 사전 가지치기 매개변수
  • 만들어진 모델을 쉽게 시각화
  • 데이터의 스케일에 구애 받지않음
  • 사전 가지치기를 사용함에도 과대적합되는 경향이 있어 일반화 성능이 좋지않음

2.3.5 결정트리의 앙상블

앙상블: 여러 머신러닝 모델을 연결하여 더 강력한 모델을 만드는 기법

랜덤 포레스트(random forest) 와 그레이디언트 부스팅(gradient boosting) : 분류와 회귀 모델을 구성하는 기본 요소로 결정 트리를 사용

2.3.6 랜덤포레스트

훈련 데이터에 과대적합되는 문제가 있는 결정 트리 문제를 회피할 수 있는 방법

• 서로 다른 방향으로 과대적합된 트리를 많이 만들어 그 결과의 평균을냄 -> 과대적합된 양을 줄일 수 있음

• 랜덤포레스트 구축

  • 트리의 개수를 정한다.
  • 트리를 만들기 위해 데이터의 bootstrap sample을 생성 ex) [‘a’,‘b’,‘c’,‘d’] 의 bootstrap sample -> [‘b’,‘d’,‘d’,‘c’] …
  • 만들어진 데이터 셋으로 결정 트리 생성
  • bootstrap sampling -> 랜덤포레스트의 트리가 조금씩 다른 데이터셋을 이용해 만들어지게함

• 랜덤포레스트 분석

  • 랜덤포레스트는 개개의 트리보다는 덜 과대적합되고 좋은 결정경계를 만들어준다.
  • 랜덤포레스트의 특성중요도 = 각 트리의 특성중요도를 취합하여 계산
  • ex. 다섯 개의 랜덤한 결정 트리의 결정 경계와 예측한 확률을 평균내어 만든 결정 경계

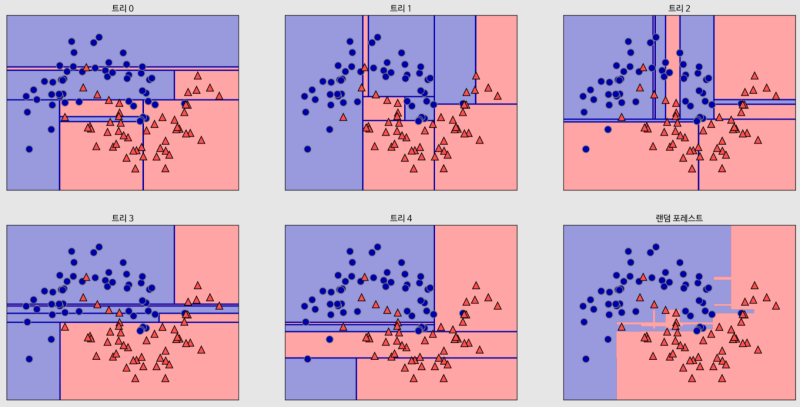
• 장단점과 매개변수
  • 매개변수 튜닝을 많이 하지 않아도 잘 작동하며 데이터의 스케일을 맞출 필요없음
  • 특성의 일부만 사용하기 때문에 결정 트리보다 깊어지는 경향
  • 같은 결과를 만들어야한다면 random_state 값을 고정
  • 텍스트 데이터와 같은 차원이 높고 희소한 데이터에 잘 작동하지 않음
  • 훈련과 예측이 느림
  • max_features: 각 트리가 얼마나 무작위가 될지 결정, 작은 값은 과대적합을 줄여줌
  • 분류: max_features=sqrt(n_features), 회귀: max_features=n_features

2.3.7 그레이디언트 부스팅 회귀 트리

• 회귀와 분류 모두 사용

• 이전 트리의 오차를 보완하는 방식으로 순차적으로 트리를 만듬(랜덤과의 차이점)

• 무작위성이 없음, 사전 가지치기 사용 - 깊지 않은 트리(1~5) 사용으로 메모리 적고 예측 빠름

• 랜덤포레스트보다 매개변수 설정에 더 민감, 잘 조정하면 높은 정확도

• learning_rate: 이전 트리의 오차를 얼마나 강하게 보정할 것인지 제어

• n_estimators를 키우면 앙상블에 트리가 더 많이 추가되어 모델의 복잡도가 커짐

• 장단점과 매개변수

  • 매개변수를 잘 조정해야하며 훈련시간이 김
  • 특성의 스케일을 조정하지 않아도 되고 이진, 연속 특성에 잘 작동
  • 매개변수: n_estimators= 트리의 개수를 지정, learning_rate= 트리의 오차 보정정도
  • n_estimators를 크게할수록 모델이 복잡하고 과대적합 가능성이 높아짐(랜덤과 차이점)
  • max_depth = 각 트리의 복잡도를 낮추는 매개변수

2.3.8 배깅, 엑스트라 트리, 에이다부스트

• 배깅(Bootstrap aggregating)
  • 중복을 허용한 랜덤 샘플링으로 만든 훈련 세트를 사용하여 분류기를 각기 다르게 학습
• 엑스트라 트리(Extra-Tree)
  • 랜덤포레스트와 비슷하지만 후보 특성을 무작위로 분할한 다음 최적의 분할을 찾음
• 에이다부스트(Adaptive Boosting)
  • 그레이디언트 부스팅처럼 약한 학습기를 사용
  • 그레이디언트 부스팅과 달리 이전의 모델이 잘못 분류한 샘플에 가중치를 높여서 다음 모델을 훈련시킴

2.3.9 커널 서포트 벡터 머신(Kernelized support vector machines)

입력 데이터에서 단순한 초평면으로 정의되지 않는 더 복잡한 모델을 만들 수 있도록 확장한 것
ex. 확장된 3차원 데이터셋에서 선형 SVM이 만든 결정 경계

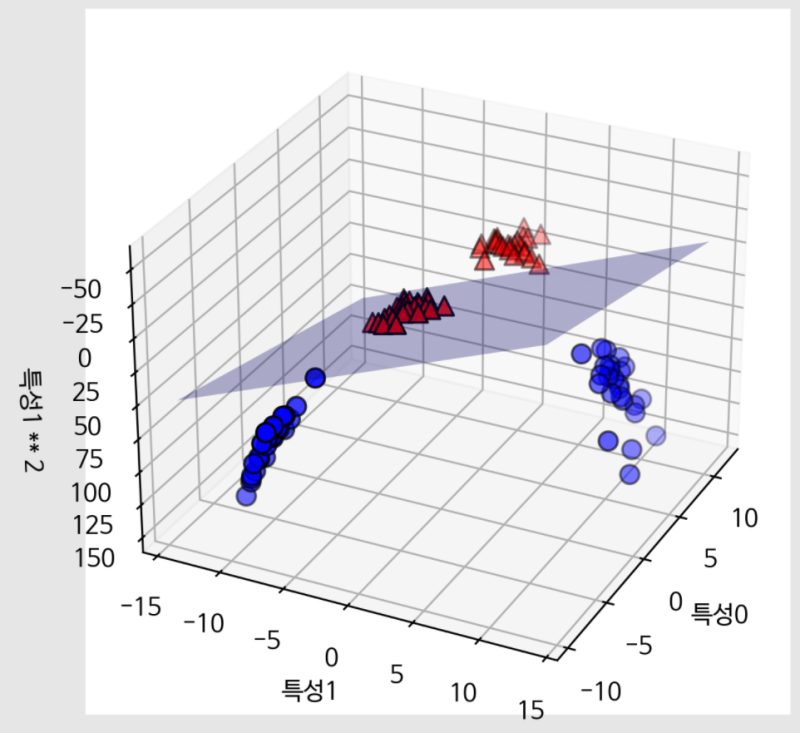
• 커널기법: 새로운 특성을 많이 만들지 않고서도 고차원에서 분류기를 학습시킴, 실제로 데이터를 확장하지 않고 확장된 특성에 대한 데이터 포인트들의 거리를 계산

• 데이터를 고차원 공간에 매핑하는 방법

  • 가우시안(Gaussian)커널: 차원이 무한한 특성 공간에 매핑
  • RBF(radial basis function)커널

• SVM 이해하기

  • 서포트 벡터(support vector): 두 클래스 사이의 경계에 위차한 데이터 포인트
  • 새로운 데이터 포인트에 대해 예측하려면 서포트 벡터와의 거리를 측정

• 데이터 포인트 사이 거리: 가우시안 커널

• 장단점과 매개변수

  • SVM은 데이터의 특성이 몇개 안되더라도 복잡한 결정 경계를 만들 수 있음
  • 샘플이 많을 때 잘 맞지 않음
  • 데이터 전처리와 매개변수 설정이 까다로움
  • 분석하기 어려움
  • 규제 매개변수 C: 어떤 커널을 사용할지 + 각 커널에 따른 매개변수

2.3.10 신경망(딥러닝)

다층 퍼셉트론(Multilayer perceptrons, MLP)

• 중간단계를 구성하는 은닉 유닛(hidden unit)

• 많은 계수(가중치=w)를 학습해야함: 각 은닉 유닛의 가중치 합 계산 후 결과에 비선형 함수(ReLU or hyperbolic tangent)를 적용

• 많은 은닉층으로 구성된 대규모 신경망 = 딥러닝

• 장단점과 매개변수

  • 대량의 데이터에 내재된 정보를 잡아내고 복잡한 모델 만들 수 있음
  • 학습이 오래걸림
  • 데이터 전처리에 주의해야함

• 신경망의 복잡도 추정

  • 중요한 매개변수: 은닉층의 개수, 각 은닉층의 유닛 수
  • 복잡도에 도움이 될 측정치 = 가중치 or 계수의 수

2.4 분류 예측의 불확실성 추정

2.4.1 결정함수

샘플 공간에서 결정 영역으로 대응/매핑시키는 함수

2.4.2 예측 확률

• 데이터에 있는 불확실성이 얼마나 값에 잘 반영되는지는 모델과 매개변수 설정
• 불확실성과 모델의 정확도가 동등 -> 모델이 보정(calibration)된 것

2.5 요약

좋은 성능 = 매개변수를 적절히 선정하는 것

• 최근접 이웃: 작은 데이터셋일 경우, 기본 모델로서 좋고 설명하기 쉬움

• 선형 모델: 첫 번째로 시도할 알고리즘, 대용량 데이터셋 가능, 고차원 데이터에 가능

• 나이브 베이즈: 분류만 가능, 선형 모델보다 훨씬 빠름, 대용량 데이터셋과 고차원 데이터에 가능. 선형 모델보다 덜 정확

• 결정 트리: 매우 빠름. 데이터 스케일 조정 필요 없음. 시각화하기 좋고 설명하기 쉬움

• 랜덤 포레스트: 결정 트리 하나보다 거의 항상 좋은 성능을 냄. 매우 안정적이고 강력함. 데이터 스케일 조정 필요 없음. 고차원 희소 데이터에는 잘 안맞음

• 그레이디언트 부스팅 결정 트리: 랜덤포레스트보다 조금 더 성능이 좋음. 랜덤 포레스트보다 학습은 느리나 예측은 빠르고 메모리를 조금 사용. 랜덤 포레스트보다 매개변수 튜닝이 필요함.

• 서포트 벡터 머신: 비슷한 의미의 특성으로 이뤄진 중간 규모 데이터셋에 잘 맞음. 데이터 스케일 조정 필요. 매개변수에 민감

• 신경망: 특별히 대용량 데이터셋에서 매우 복잡한 모델을 만들 수 있음. 매개변수 선택과 데이터 스케일에 민감. 큰 모델은 학습이 오래 걸림.

출처:Introduction to Machine Learning with Python 책을 보고 정리한 내용입니다.