- 전체보기(86)
- 알고리즘 스터디(22)
- 알고리즘(21)
- TIL(13)
- 그리디(10)
- Java(8)
- 백트래킹(5)
- 유니온 파인드(4)
- 브루트포스(4)
- 투포인터(3)
- 다익스트라(3)
- 프로그래머스(3)
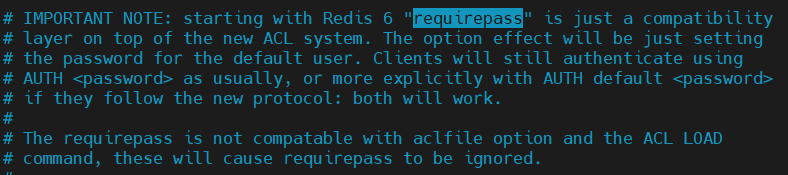
- redis(2)
- 크루스칼(2)
- mysql(2)
- 트리(2)
- env(1)
- 오류해결(1)
- Alarm(1)
- mongodb(1)
- 최소 스패닝 트리(1)
- docker(1)
- CS(1)
- 완전탐색(1)
- 부분집합(1)
- 데이터베이스(1)
- is(":checked")(1)
- C(1)
- 트러블슈팅(1)
- 백준(1)
- 프림(1)
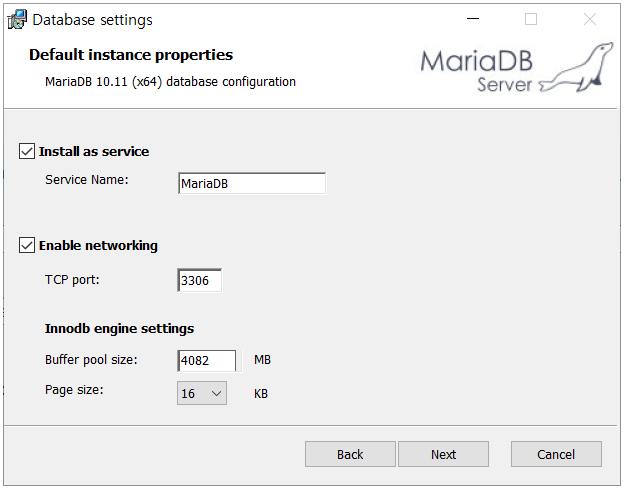
- MariaDB(1)
- 구현(1)
- 자바(1)
- Grafana(1)
- DFS(1)
- 그래프(1)
- 자바 swing(1)
- docker compose(1)
- 스프링(1)
- git(1)
- sql(1)
- 자료구조(1)
- jenkins(1)
- 플로이드워셜(1)
- DP(1)
- 벨만포드(1)
- 중복순열(1)
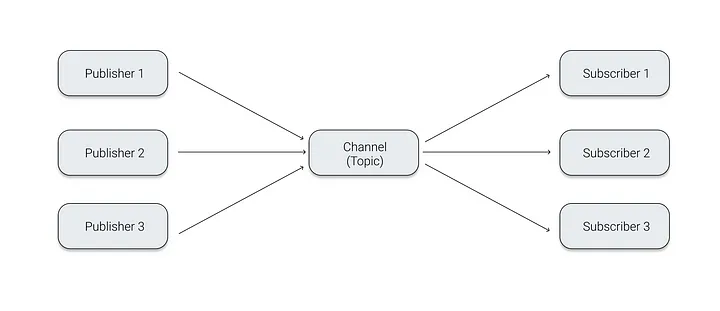
- sse(1)
- JavaScript(1)
- eclipse(1)
env.yml vs env.properties
env.properties : application.properties에 선언후 비밀키 내용을 env.properties에 통째로 입력

[JS] Node.js는 싱글스레드인가?
무료하게 앉아있는 연말... 새로운 주제를 접하게되어 정리해보려고한다.시작은 멀티쓰레드와 비동기를 동일시하는 주제에서 시작이다.결론부터 말하자면 당연히 아니다. 워낙 스레드를 이용해서 비동기/동기개념이 다뤄지고있다보니 처음 접하는 사람은 스레드를 사용해서 해당개념을 이
[Java] HashMap
문제를 풀던 도중 객체에 equals, hashcode를 왜 오버라이드하는지 알수있게하는 문제를 발견했다.해시맵의 put 작동방식은 다음과같다.먼저 같은값이 있는지 체크있으면 그곳에 값을 대입위에서는 Map<Point, Integer>으로 객체의 카운팅을 하는 맵
[SQL] DATE_ADD 등 날짜 관련 SQL
DATE_ADD 날짜 관련해서 일수를 더하고 빼는 함수이다 위 함수를 실행하면 이 나오게된다. 이는 DateFormat함수로 변환해주면 이쁘게 포장된다. DATE_SUB 자매품 DATE_SUB함수도 있다. 양식은 같다. DATEDIFF 각 날짜의 차이를 구하는

[Novelit] Aws 요금 이슈
AWS 프리티어 사용량 초과를 대비해 예산 알림을 0.01$에 설정을 해놓았었다.그라파나 세팅후 3일만에 이메일 알림이 오게 되는데...바로 그만쓰라는 무언의 압박 메세지...받자마자 든 생각이 용량 초과는 아니었을것이라는 생각이다.AWS EC2용량은 한개만 굴리기때문
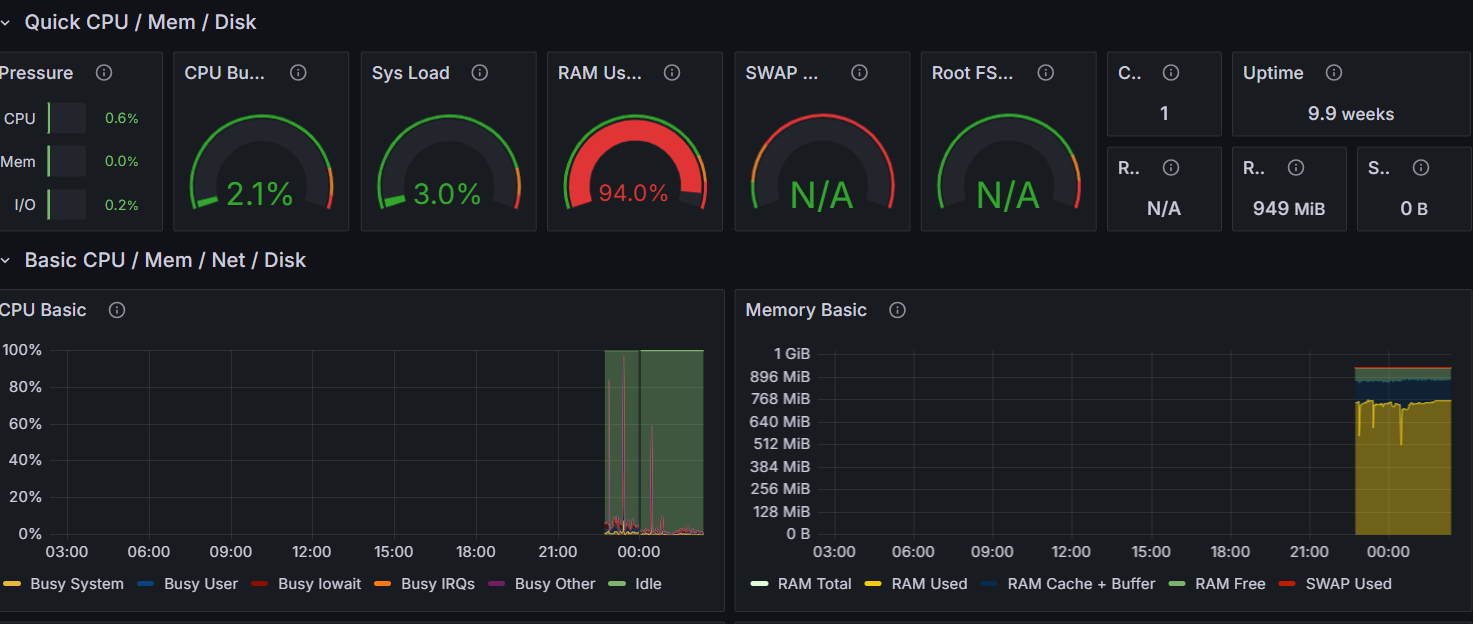
[Novelit] Grafana 관측 이슈
grafana를 구축하고 둘러보는데, 좀 큰 이슈같아 보이는것을 발견했다.job을 변경해보는데 위와같이 novelit-aws(production 서버) 에서 RAM 사용량이 94퍼가 관측된것...문제가있는지 찾아보고, 조치를 취해야겠다. 모니터링 환경을 구성하니, 확
[Java] 초기화
14500 테트로미노 문제를 풀던중 한가지 문제를 마주하였다.바로 배열의 초기화에대한것.자바에서 초기화는 다음과 같다.이 함수를 보고 여태 한 생각은 처음 메모리공간이 O(1)시간 만에 디폴드값으로 할당되는줄알았다. (부끄럽게도)하지만 테트로미노를 풀던 중,전역으로 정
[Spring Boot JPA] Audit
자동으로 시간을 넣어주는 기능.몰랐는데 spring boot에서 지원하는 기능이아니라, jpa에서 지원하는 기능이다.이걸 redis에 적어서 오류가 난듯?
[Novelit] Docker-compose에 Grafana, Node-exporter, Prometheus 설치
파일 위치를 잘 결정해야한다.volumn : 원격에서 위치 : docker 컨테이너 안에 마운트 시킬 위치.env 파일 사용을 지원하지않는다.주소는 배열안에 문자열 형식으로 넣어주어야한다.docker-compose에 잘 적어놨다면 추가 할것이 딱히 없다.
[Java] Stringbuilder
부분 문자열을 삭제하는 메소드다.startIndex를 포함하며, endIndex를 포함하지않기때문에, +1한 인덱스를 넣어준다.여기서 시험삼아서 돌려봤는데, endIndex는 문자열 길이를 초과해도, 에러를 발생시키지않는다. 이미 끝부분이 문자열의 length()까지로

[Spring] AssertionFailedError : Actual Null
서비스 테스트했을때 발생한 문제다.ProductServiceTest.classProductService.addProduct다음과같은 상황에서 테스트를 실행하면 이런 에러가 뜬다이는 stub도 잘되어있고 뭐가 문제일까하며 찾아봤는데, 객체가 저장되었는데 null값이 반환
[BE] Java Spring
1. @Embedded, @Embeddable 2. record 3. @NoArgsConstructor(access = AccessLevel.PROTECTED) 4. @Repository
힙(heap)
기본 배열로 구성편의를 위해 인덱스를 1부터 시작기본 완전 이진 트리 형태를 사용최대힙을 기준으로 설명가장 마지막 인덱스 n + 1에 삽입n + 1의 부모와 계속 비교해나가며, 값이 크면 (부모의 값이 작으면) 교환한다.