Dot product Self-attention은 Lipchitz인가?

트랜스포머에 전형적으로 쓰이는 dot-product self-attention을 생각해봅시다.

정확히는 (scaled) dot-product multihead self-attention

$x_1, ..., x_N$의 $N$-length sequence를 가정해보자(각 원소는 실수).

그러면, 아래와 같이 행렬로서 매트릭스를 표현할 수 있다(각 원소의 차원은 $D$).

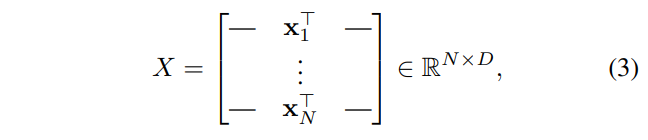
Dot-product Multihead self-attention은 실질적으로 같은 도메인끼리의 맵핑함수이다.

$\mathbb{R}^{N\times D}$ $\rightarrow$ $\mathbb{R}^{N\times D}$

특히, 위 과정을 H heads로 나누어 병렬적으로 진행하게 됩니다.

즉, $D$ 차원을 $8$개의 head로 나눈다든지..

즉, 실제로는 따지고 보면 각각의 HEAD가 아래의 매핑을 따릅니다.

$\mathbb{R}^{N\times D}$ $\rightarrow$ $\mathbb{R}^{N\times D/H}$

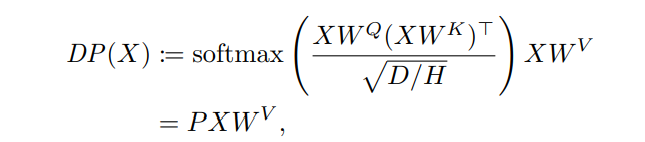
위에서 Query, Key, Value의 embedding을 책임지는 $W^{Q}, W^{K}, W^{V}$는 모두 $D\times D/H$ 차원을 같습니다.
물론 각각의 head에 대해 다르게 존재하는 parameter이며, 학습의 대상입니다.

위에서 말하는 $P$는 softmax의 output을 말합니다($N\times N$ 차원).

아무튼, soft max의 input 또한 $N\times N$이 되며, 각각의 low 차원을 따라서 softmax가 진행됩니다.

최종적인 output은 결국 모든 heads를 따라 concat되어 $N\times D$ 차원의 matrix와 $D\times D$ 차원의 가중치 $W^{O}$와 곱해져 $N\times D$ 차원의 final output $MHA_{DP}(X)$가 됩니다.

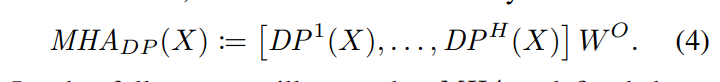
결국 위의 식은 $MHA map$이 non-trivial하다는 가정 하에 립시츠가 아니게 됩니다(왜?).

non-trivial : $W^{Q},W^{K},W^{V},W^{O}\ne 0$

특히, $MHA$ 자체는 각 head의 attention이 선형 결합(concat + matrix product)한 것에 지나지 않기 때문에, $MHA$의 각 head의 Dot-product만 립시츠가 아님을 보이면 됩니다.

---

또한, 위에서 정의한 softmax의 output $P$가 stochastic matrix인 점을 주목해봅시다.
즉, $P$의 각 원소들은 non-negative이며, row 간 합은 1이 됩니다

$X$에서 하나의 row만 떼서 생각한다면 $x_i's$, 즉 $D$차원의 token이 됩니다.

이 때, 각 $x_i's$들의 행렬 $A$에 대한 linear transformation은 사실상 $XA^{T}$로 나타낼 수 있습니다(right multiplication).
그렇기 때문에 $XW^{V}$ 또한 linear map이라 할 수 있고, 따라서 립시츠입니다.

linear $\rightarrow$ lipschitz 증명
https://math.stackexchange.com/questions/3656151/a-linear-transformation-of-mathbbrn-is-lipschitz

이 때, $f(X)=PX$에 대한 맵핑을 생각해봅시다.

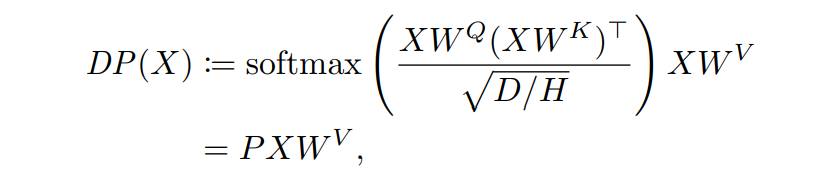
즉, 위에서 $XW^{V}=A$는 선형이므로, $PXW^{V}=PA$의 매핑을 보면 됩니다.
하지만, 모두가 알다시피 $P$는 softmax이기 때문에 그 자체로 non-linear function입니다.
즉, $f(X)=PX$는 $X$에 대한 non-linear function입니다.

---

출처

https://arxiv.org/pdf/2006.04710.pdf