[정리] GAN / DCGAN

temp·2021년 10월 31일

AI DCGAN Generative Model gan

Generative Model

목록 보기

13/30

간단히 메모한 글입니다.

주로 Generative Model(생성모델) 중에 가장 널리 쓰이는 모델로 GAN, VAE가 존재한다.

해당 모델들이 궁극적으로 추구하고자 하는 목표는 아래와 같습니다.

생성된 이미지의 질
다른이미지를 만들 수 있는 입력값

VAE에서는 ELBO, KL Divergence를 이용해 생성 이미지의 질을 높히도록 학습합니다.
또한, 가우시안 분포를 가정하고 샘플링하기 때문에 정해진 분포 내에서 다른 값을 샘플링해 이용한다면 학습 데이터와 다른 분포를 갖는 데이터 또한 생성할 수 있습니다.

KL-Divergence을 이용한 Regularization을 주는 VAE의 방법은 MLE에 비해 MNIST 쪽에선 나름 합리성이 있다지만(인간이 보기에 그럴듯한), 실질적으로 VAE의 성능은 안 좋은 단점도 분명 존재합니다.

즉, VAE는 현실적이지 못하고 블러리한 이미지를 만들곤 하는데 이에 대한 이유를 아래와 같이 추측할 수 있습니다.

평가 지표가 좋지 못하다.
- '그럴듯하다' 라는 것은 결국 인간의 주관성이 들어갈 수밖에 없습니다.
이미지의 고차원적인 정보를 결국 저차원 매니폴드에 잘 담지 못했다. 인코더의 성능이 안 좋았다거나..

GAN은 VAE와 약간 다른 접근법을 택합니다.

GAN은 DNN으로 구성한 분류기를 사용하고, 가우시안 분포에서 노이즈만을 추출해 input으로 사용했습니다.

모델의 아키텍처는 아래와 같습니다.

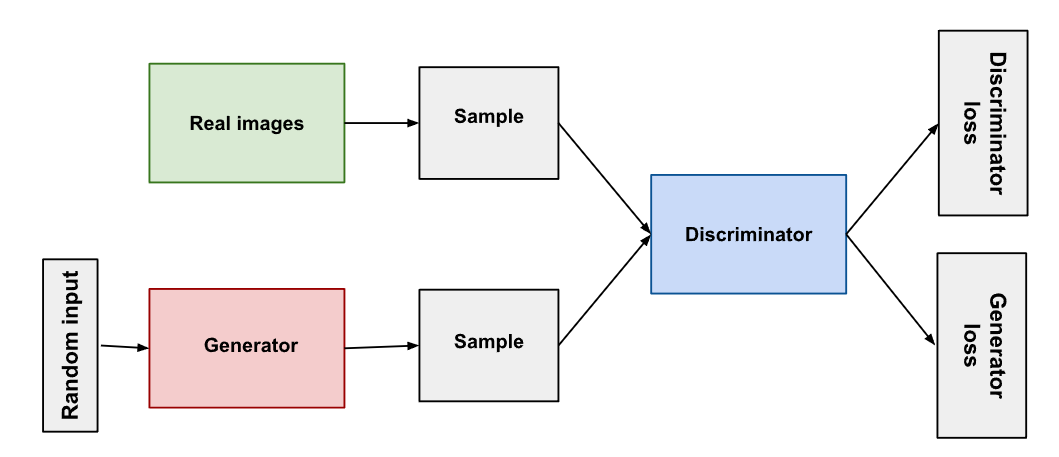
위의 그림에선 Random Input은 VAE와 다르게 실제 이미지에서 추출한 값(분포)가 아니고, 그냥 평균과 분산이 고정된 정규분포에서 추출된 노이즈입니다.

이러한 Latent vector를 받아서 이미지를 생성하게 되는데, GAN의 기본이 되는 논문에서는 FFN을 사용합니다(단순 MLP).

즉, 위처럼 그냥 Linear 층만을 사용해 latent vector를 이미지 차원 개수까지 늘립니다.

즉, $(128,)$ 차원 -> $(256, 256)$ 차원으로 만드는 것이 Generator의 역할입니다.

이게 실질적으로 어떻게 가능할까요?

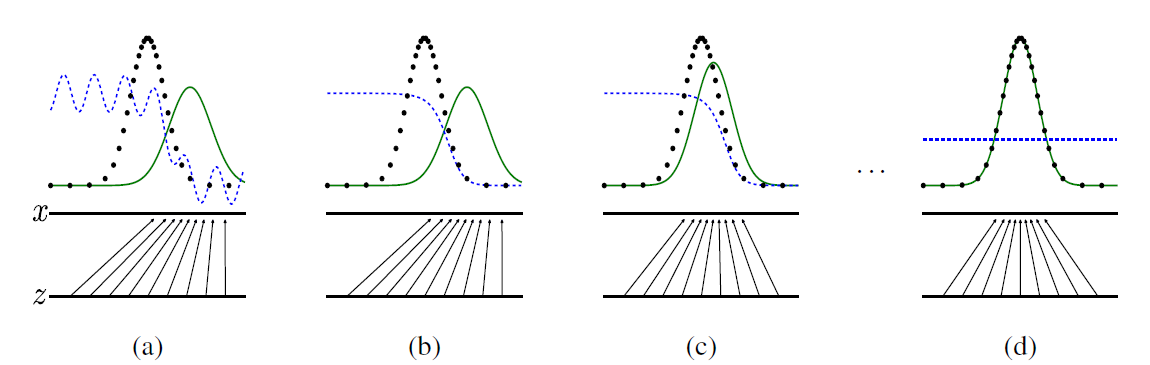
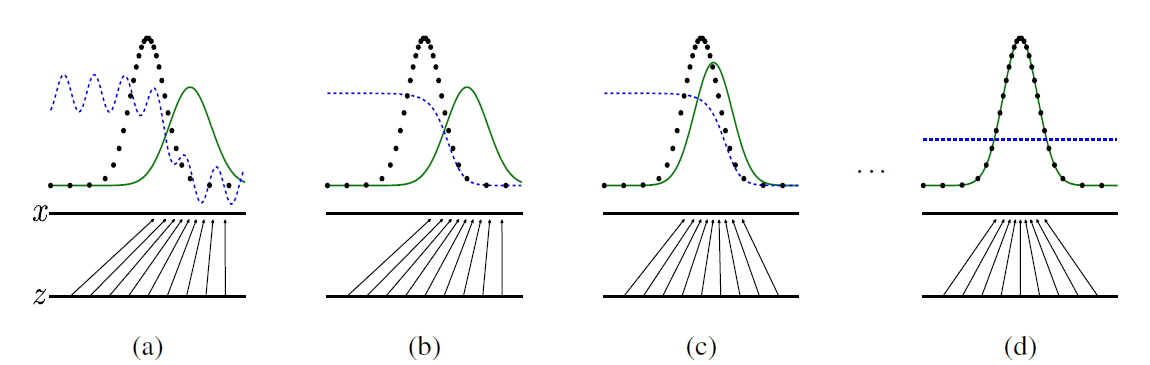
실제 이미지의 분포는 검정색 점선, 생성(가짜)이미지의 분포는 녹색 실선, 판별자의 분포는 파란색 점선입니다.
위 그림을 보면 초창기에는 판별자(파란색 점선)이 진짜와 가짜를 잘 구별해내다가, 마지막에 가짜 이미지가 진짜 이미지 분포를 잘 모사했을 경우 판별 확률 0.5로 제대로 구별하지 못하는 모습을 볼 수 있습니다.

간단히 말하면, 판별자는 실제 이미지와 생성된 이미지 두개를 받아 이진 분류 태스크를 수행하는데, 라벨을 지정해줄 수 있기 때문에 지도학습과 똑같다고 볼 수 있습니다.

아무튼, 이 모든 것은 GAN의 목적함수로 인해 가능합니다.

$x$ : 실제 이미지 데이터
$z$ : 가짜 이미지 분포에서 추출한 잠재 벡터

기존의 GAN 논문에서는 생성자가 최적화되었을 때 왜 실제 이미지를 잘 모사할 수 있는 지에 대한 수식이 담긴 증명이 존재합니다.

판별자 관점에서는,
실제 이미지는 1에 가깝게, 가짜 이미지는 0에 가깝게 판별하는 것이 판별자의 목표란 사실을 위 식에 도입하면 위의 목적함수를 최대화하는 것이 판별자의 목표가 됩니다.

실제 이미지 <-> 1
가짜 이미지 <-> 0

위 사실을 이용해 BCE Loss를 도입한다면 결국 최소화할 판별자의 손실함수는 아래와 같이 기술할 수 있습니다.

$Loss_D=-y_1Log(D(x))-(1-y_0)log(1-D(G(z)))$
( $y_1=1, y_0=0$ )

이 때, 좌측의 real-loss인 $-y_1Log(D(x))$ 와 우측의 fake-loss인 $-(1-y_0)log(1-D(g(z)))$ 는 배치 단위로 각각 따로 계산된 다음, 마지막에 합쳐집니다.

특히, 코드 상으로 본다면

real-loss : $BCE(x, 1)$
fake-loss : $BCE(G(z), 0)$ 이 된다.

자세한 내용은 여기 참고

생성자 관점에서는,
마찬가지로 위의 minmax 식을 최소화하면 됩니다

즉, $log(1-D(g(z))$ 를 최소화 하면 됩니다.

이는 일반적으로 수렴시키기 쉽지 않은 issue(GAN paper)가 존재해,

$minimize \; log(1-D(g(z))$ 대신
$minmize \; -log(D(g(z))$ 로 대체해 사용합니다.

즉,

Generative-loss : $BCE(G(z),1)$
로 손실함수를 구현할 수 있습니다.

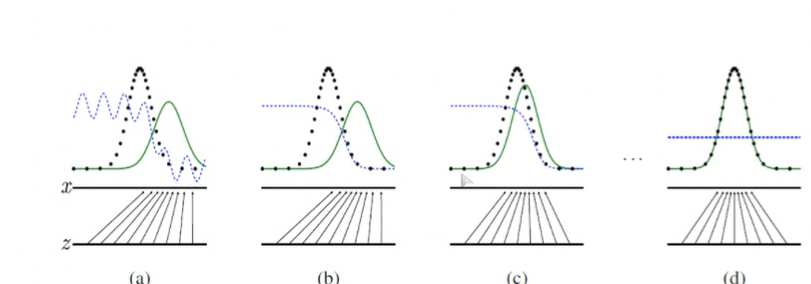
(파란색은 Discriminator다 !!)

결국, 하나의 미니배치 내에서 학습하는 과정은 아래와 같습니다.

z를 샘플링해서 Generator $G$ 가 가짜 이미지 G(z)를 생성해냅니다.
생성 이미지 G(z)와 실제 이미지 $x$ 를 판별자에 통과시켜 예측 값을 반환합니다.
예측 값을 이용해 생성자와 판별자의 loss를 계산합니다.
LossG를 이용해 생성자 업데이트
LossD를 이용해 판별자 업데이트

하지만, 당연히 이진분류 태스크인 판별 태스크가 훨씬 쉽습니다. 그렇기 때문에 판별자가 빠르게 학습해버리면 생성자의 식 중 Log 값이 바로 0이 되버린다, 그렇다는 것은 Loss가 무한대가 되버리고 당연히 학습은 개판이 될 수 있습니다.

즉, 그렇기 때문에 생성자를 3~7회 업데이트할 때 판별자를 1회 업데이트하는 등의 방식이 사용될 수 있지만, 완벽한 방법은 아닙니다.

DCGAN

Paper: https://arxiv.org/abs/1511.06434v1

여기서, 이미지를 활용하는 모델이기 때문에 Vanilla GAN에서 사용한 FFN보다는 Convolution layer를 사용하는 게 좋겠죠?

Conv layer를 통해서 곡선, 면, 모서리 등의 spatial한 정보를 잘 다룰 뿐더러 넓게 receptive field를 형성할 수 있으며, 이런 층별 역할을 통해 좋은 샘플을 또한 생성할 수 있습니다.

다만, 이를 통해 저희가 생성 모델을 컨트롤할 수 있는 지는 별개의 얘기입니다.

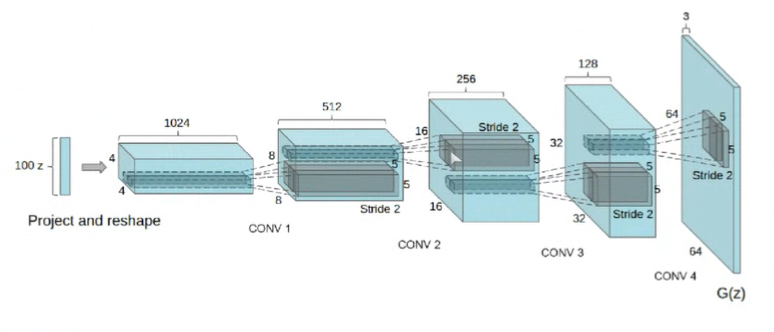
생성자 $G$ 에서는 convolution 과정을 반대로 거쳐야 이미지를 생성할수 있습니다.

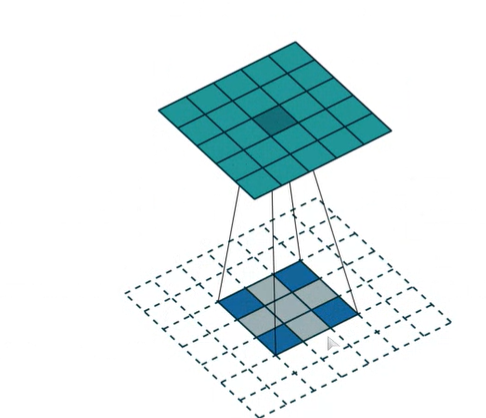
즉, 위처럼 2x2 크기의 이미지를 5x5로 키우기 위해서는 이미지 사이사이, 그리고 바깥에 약간의 패딩을 준 다음 컨벌루션 연산을 수행하면 됩니다.

두 개의 latent vector $z, z'$ 를 이용, 보간법을 활용한다면 이미지가 서서히 변하는 사실을 알 수 있습니다.

즉, $z$ 에서의 연속적인 변화가 실제 이미지의 변화를 이끌어낼 수 있습니다.
$z$ 가 의미 있는 정보를 가지고 있다고 봐도 무방합니다.

또한, 학습을 잘 하게 된다면 latent space에서 벡터끼리 연산을 수행할 수 있게 됩니다.

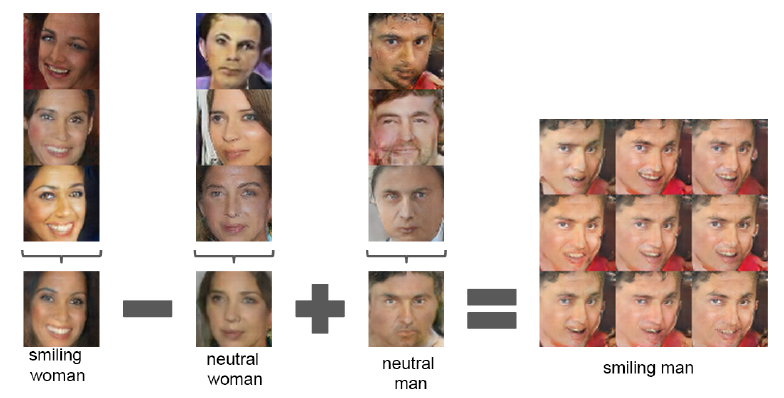
여기서 z vector를 조정함으로써 '웃음, 남성, 여성'이라는 특징을 조절할 수 있게 됩니다.

이렇듯 잠재벡터 $z$ 를 조절해 생성 이미지를 조절할 수 있는 것 뿐만 아니라, CNN을 사용하는 만큼 우리는 Filter를 활용할 수도 있습니다.

DCGAN 과정에서는 $z$ 를 실제 데이터 $x$ 와 유사한 샘플 $G(z)$ 에 매핑하는 함수 $G$ 를 학습하게 됩니다.
그렇다는 것은, 생성자 $G$ 의 Convolutional Layer에 실제 데이터 $x$ 에 존재하는 특정한 특징들(창문 등)을 담당하는 filter가 있을 것이라 예측할 수 있습니다.

즉, 창문을 만든다는 필터가 있을 것이고, 그 필터를 제거한다면, 창문을 제거할 수 있는 것입니다.

이에 대한 예시는 아래 그림과 같습니다.

즉 필터에도 의미가 있고, 잠재 벡터 $z$ 에도 의미가 있습니다.

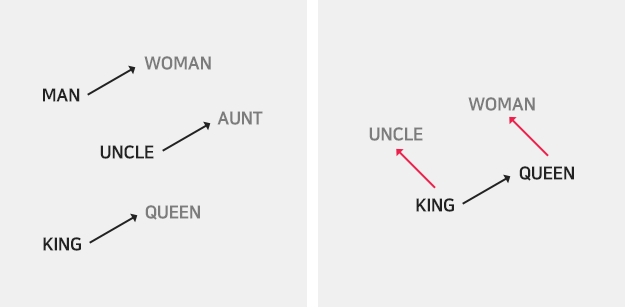
이는 때때로 자연어 처리에서도 중요하게 다루곤 합니다.
가령 KING과 UNCLE의 관계와 QUEEN과 WOMAN의 관계를 동일시할 수 있다든지..

아무튼, 벡터 공간에서의 연산이 유의미해질 수 있다는 것은 굉장히 큰 잠재력을 가지고 있습니다.

VAE를 GAN과 다시 비교해봅시다.
VAE는 GAN에 비해 분명한 지표를 가지고 있어 '모델 간' 성능 비교가 굉장히 쉽습니다.

단, GAN은 모델 간에 성능을 비교하기가 너무 어렵습니다. 가우시안 분포, KL발산 등을 가정하지 않고 곧바로 데이터로부터 학습하게 되니까요.

하지만, 실제 분포를 가정하지 않기에 오히려 더 부드러울 수 있습니다.

만약 위에서 실제 데이터 분포(검은 점)이 정규분포에서 약간 어긋난, 예를 들어 t분포라면 어떨까요?

VAE는 정규분포를 이미 가정을 해버렸기에 분포를 완벽하게 모사할 수 없고, 겹치지 않는 지역에서는 블러리하다든지, 어딘가가 뭉개진다든지 실제 데이터와 어긋난 데이터를 생성할 수도 있습니다.

단, GAN은 그러한 가정을 하지 않기 때문에 가우시안 분포가 아닐지라도 그대로 따라갈 수 있게 됩니다.

(VAE는 Likelihood를 최대화 하는 과정에서 확률들이 옆으로 조금씩 흐를 수 있습니다(?))

생성 결과

보완

1.Vanilla GAN

Q. GAN에서 min max loss가 이론적으로 타당하다는 건 알겠는데, 판별자에서 2개, 생성자에서 1개, 즉 3개의 loss term이 모두 BCELoss로 구현이 될 때 어떤 식으로 식이 성립하는 지 궁금합니다. 가령, 생성자에서는 min max loss에서 log(1-D(g(z))를 최소화하는 것을 목표로 하는데, 이는 -log(D(g(z))를 최소화하는 것과 동치인건가요? (즉, BCELoss(D(g(z)), 1)

A.
논문에 Binary Cross Entropy에 관련된 이런 저런 내용들($log, KL, JS $...)이 있습니다만.. 우선 아래를 봅시다

식 출처 : https://stats.stackexchange.com/questions/534044/how-to-use-binarycrossentropy-intutively-for-generator-network-in-dcgan-model

참고하면 좋을 논문
Good fellow, NIPS 2016 Tutorial:
Generative Adversarial Networks
21p.

2.DCGAN

Q.생성자를 학습할 때도 D(G(z))(즉 판별자 D를 이용해 가짜 샘플 G(z) 판별) 명령어를 사용해 output(real or fake)를 내는데, 이게 어떻게 생성자 G에게 그래디언트가 전달되는 거죠? output → 판별자 D → 생성자 D 이런 순서로 역전파가 되는건가요?)

g_loss.backward()
optimizer_G.step()
optimizer_D.zeros_grad()

(대충 코드)

최종적인 $loss$ 로부터 Gradient를 역전파하긴 하지만, $D\rightarrow G$ 로 흘러가는 Gradient를 이용해 생성자 $G$ 만 업데이트하고, 이 때 $D$ 에 누적된 그래디언트는 없애게 된다(물론 업데이트가 끝나면 $G$ 또한 그래디언트를 버리겠지만).

결론적으로 $D$ 는 $G$ 의 그래디언트를 구하는 데만 사용할 뿐 업데이트는 $G$ 만 이루어진다 !

temp

이전 포스트

Test time Training Test for SPADE

다음 포스트