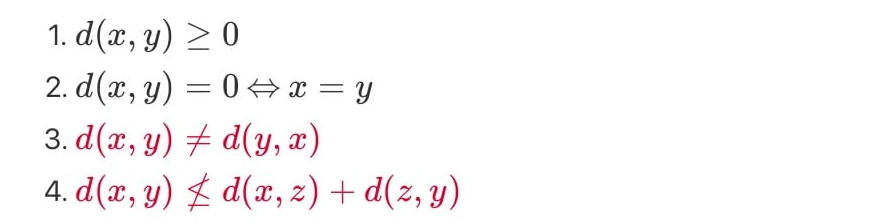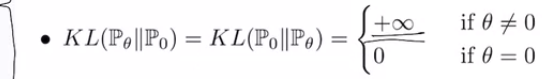[정리] Metric for WGAN

Vanilla GAN의 문제는 아래와 같습니다.

GAN에서 BCE loss를 사용할 때에는 기울기소실이 일어난다.

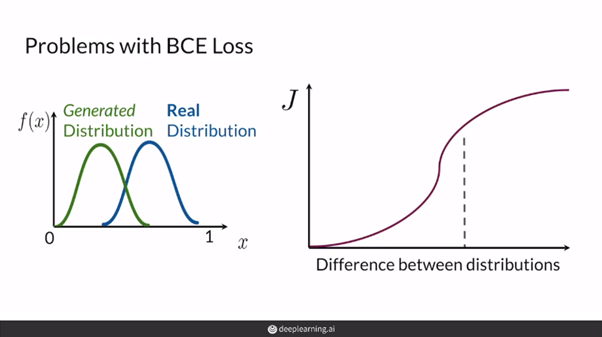
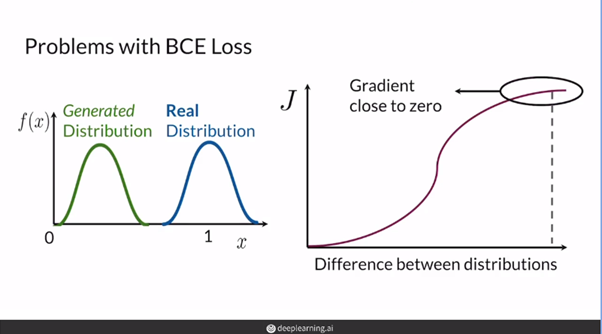
• 즉, 위의 그림과 같이 분포가 상당히 멀다면(즉, 아직 모델이 데이터의 분포를 잘 모사하지 못했다면) BCELoss의 특성 상 좋은 gradient feedback을 주기 힘들다.

[출처 : deeplearning.ai "Build Basic Generative Adversarial Networks (GANs)" 강의자료]

이를 해결하기 위해 WGAN이 나왔는데, WGAN을 정리하기 앞서 다양한 거리(Metric)에 대해 정리하고 넘어갑시다.

거리(metric) & 확률분포

해당 단락 내 모든 그림 출처 : Wasserstein GAN 수학 이해하기 I (임성빈)

거리(metric)의 예시

실수 & 복소수 공간의 절대값( | · | )

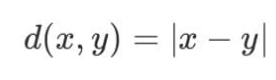
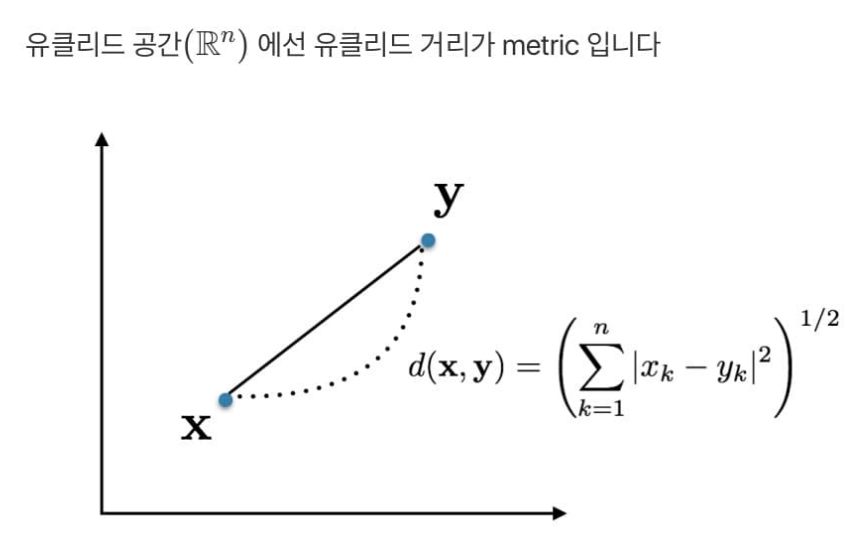
유클리드 공간에서 유클리드 거리

힐베르트 공간의 내적

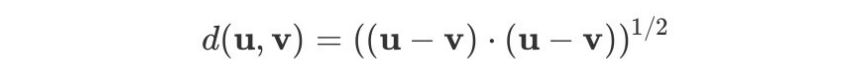
힐베르트 공간 : 내적이 정의되는 Complete vector space
ex ) 유클리드 공간 , L2-공간 (함수들의 집합)...

함수공간에서의 거리

---

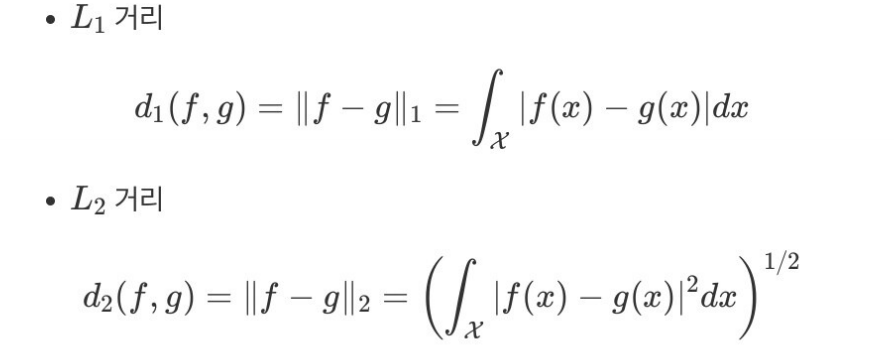
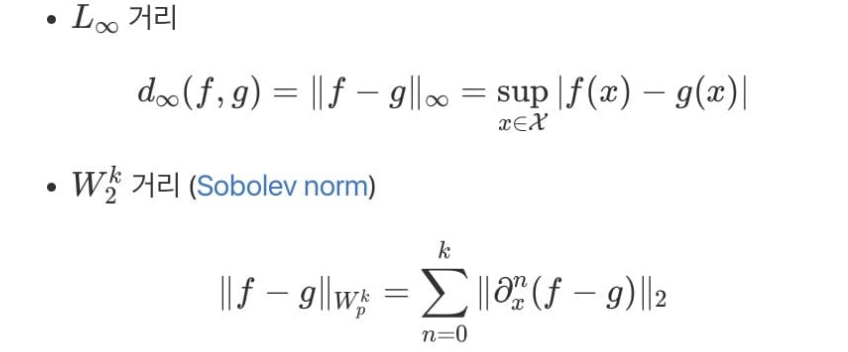
거리와 수렴

어떤 공간의 거리(metric)개념이 중요한 이유는 수렴(convergence)의 개념을 도입할 수 있기 때문이다.

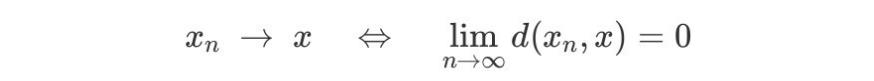
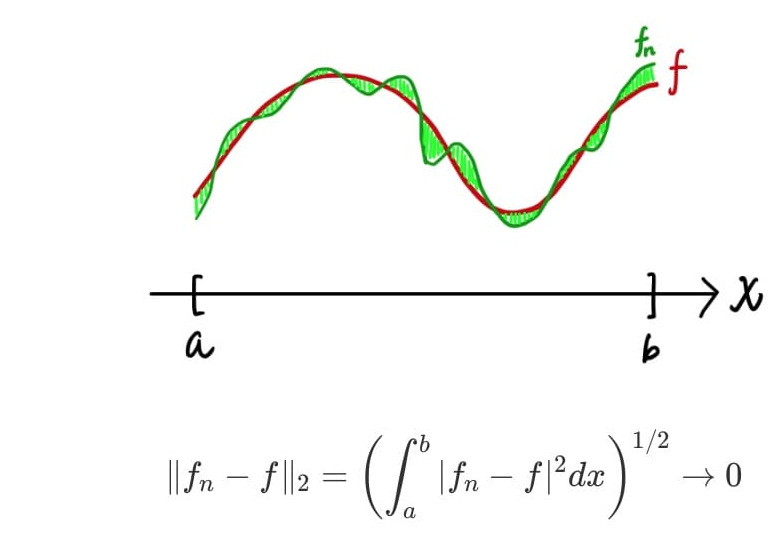
예를 들어, 함수 간 거리 중 L2-거리를 생각해보자.

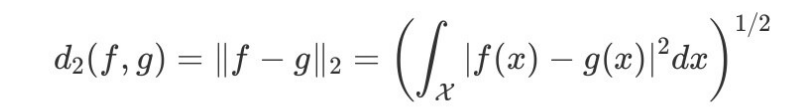
만약, 비교할 두 함수가 $f_n$과 $f$라 하면 , $f_n$과 $f$의 차이를 제곱해서 적분한 값이 0으로 수렴할 수 있게 만들 수 있다면 L2-수렴 한다고 할 수 있다.

균등수렴

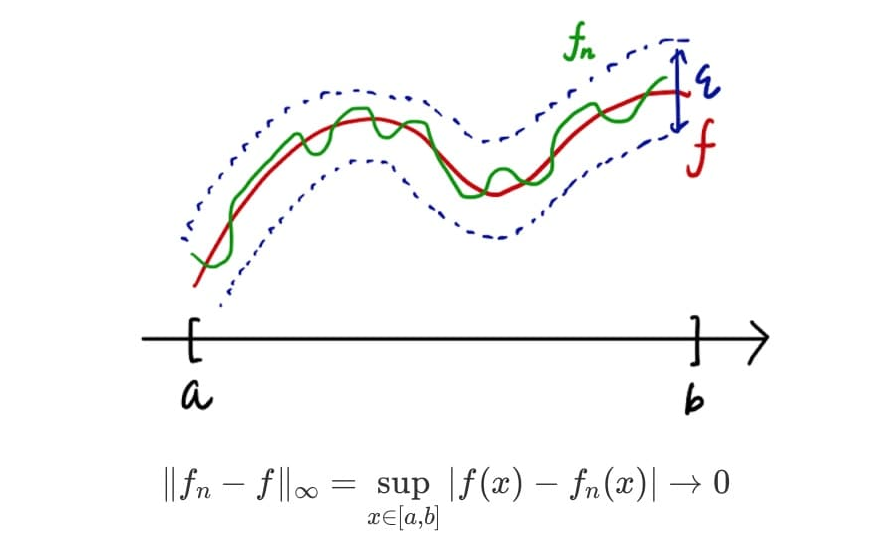
만약, 추가적으로 x에 상관없이(모든 x에 대해) $f_n$과 $f$의 차이를$\epsilon$보다 작게 만들 수 있다면 $L_\infty$수렴 한다고 할 수 있고, 이를 달리 말하면 균등수렴(Uniformly converge)한다고 할 수 있다.

수렴 안하는 정의역의 측도가 0

---

infimum & supremum

많은 논문을 읽다 보면 $inf$와 $sup$라는 기호를 볼 때가 많다.

infimum

$inf$는 infimum(최대하한)의 약자이다. 즉, $inf A$는 집합 $A$의 하한(lower bound) 중 가장 큰 값을 말한다. 이 때, 하한은 집합 내 모든 원소보다 작거나 같은 값이라면 여러 개라도 가능하다.

supremum

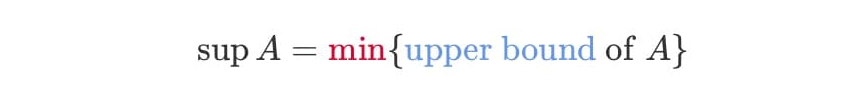
$sup$는 supremum(최소 상한)의 약자이다. 즉, $sup A$는 집합 $A$의 상한(upper bound) 중 가장 작은 값을 말한다. 역시, 상한은 집합 $A$의 모든 원소보다 크거나 같은 값이라면 여러 개라도 가능하다.

가령, 집합 A={3,4,5}의 하한은 3, 2, 1, 0, -1, -1.5, ... 등 무수히 많다. 이 중 가장 큰 값은 3이므로 $inf A$ = 3

해당 개념들이 자주 쓰이는 이유는 집합이 최소(최대)값은 가지지 않을 수 있지만, sup(inf)는 항상 존재하기 때문이다.

ex) A={1, 1/2, 1/3........} (최대(이자 sup) : 1, 최소 : x, inf : 0

---

두 확률분포간의 거리를 나타내는 지표들

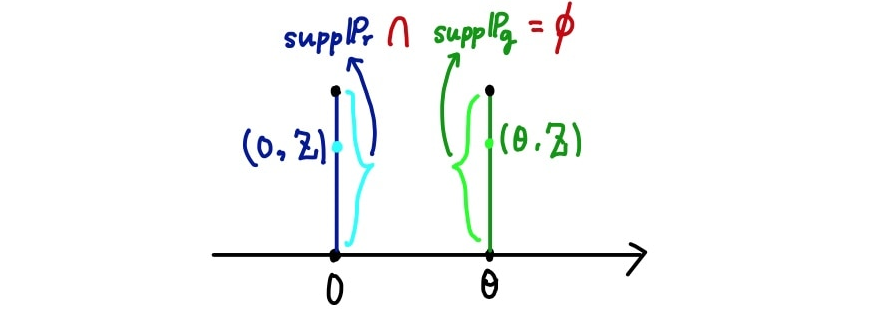
우선, 아래와 같은 분포를 생각해보자.

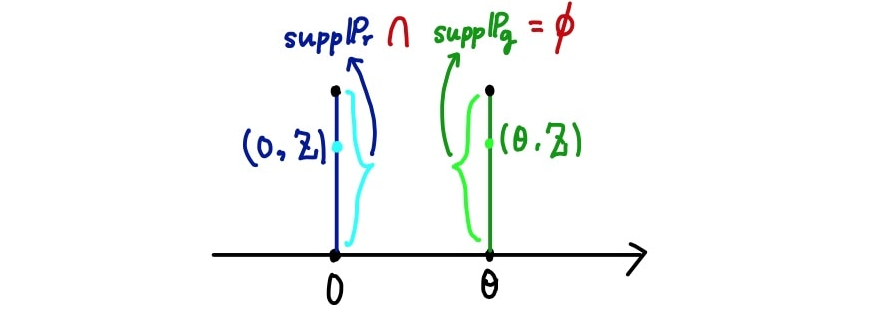
GAN을 학습하는 데 있어서 우리가 학습시키고자 하는 생성모델의 분포(여기서 $\mathbb{P}_g$)와 학습 데이터의 분포(여기서 $\mathbb{P}_r$) 간의 거리가 먼 상황이 생각보다 많다. 즉, 위 확률분포들처럼 지지집합(가능한 사건 or 가능한 샘플들의 집합)이 아예 겹치지 않을 수 있다($\theta\ne0$).

고차원의 확률분포라면 특히 더욱 힘들 것 - 차원의저주

그래서 위의 상황일 때 두 확률분포의 거리가 어떻게 나타날 지 이따금씩 살펴보겠다.

---

1. Total Variation(TV)

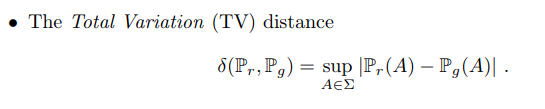
TV distance는 두 확률분포의 가능한 측정 값들 중 차이가 가장 큰 값(즉, sup) 으로 정의된다.

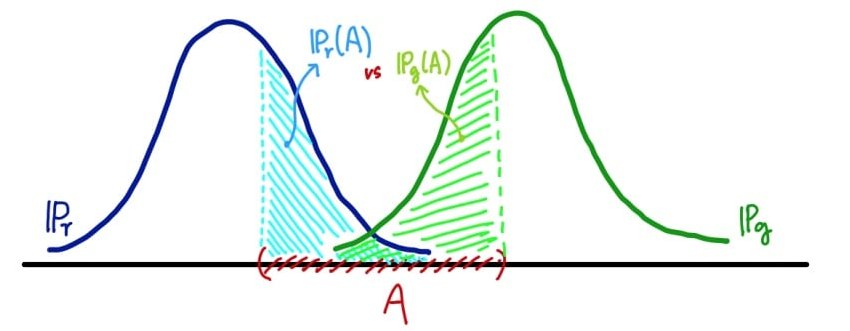
가능한 집합(혹은 사건)이 $A$로 같다 하더라도 확률 분포에 따라 당연히 측정 값(확률)은 달라지므로 이 차이나는 값들 중 가장 큰 값을 거리로 정의한 것.

예를 들어, 두 확률분포가 아예 겹치지 않으면(즉, 두 확률분포의 지지집합(support)의 교집합이 공집합이라면)TV Distance는 1이 된다(아래 그림).

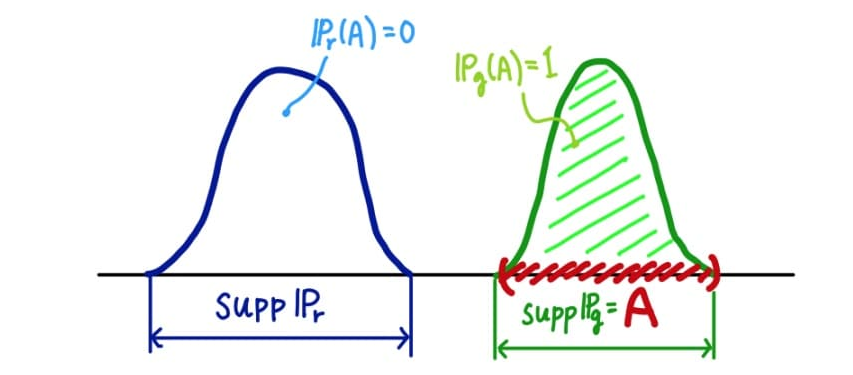
가능한 모든 집합(사건) $A\in \sigma$에 대해 거리를 살펴보는 것이기 때문에 당연히 우측의 분포 $\mathbb{P}_g$의 지지집합 또한 사건 $A$가 될 수 있다고 가정한 상황이다.
위에서 나타냈던 분포 또한 동일하게 TV=1이 나오는 것을 알 수 있다(아래 그림).

2. KL & JS Divergence

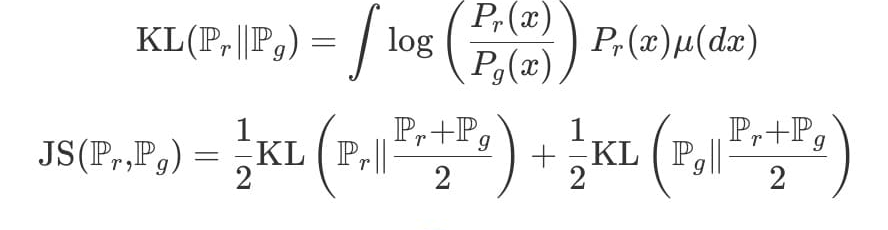
위의 KL&JS 발산은 딥러닝에서도 Classification, Cross entropy, VAE 등의 개념에서 상당히 많이 보이는 개념이다.

사실, 엄밀하게 KL 발산은 대칭성을 만족시키지 못하기 때문에 거리개념은 아니다.

하지만 위의 1,2번 조건은 만족시켜 premetric으로서 괜찮은 역할을 할 수 있어 자주 사용한다.

아무튼, 다시 아래의 예제를 가져와서 살펴보자.

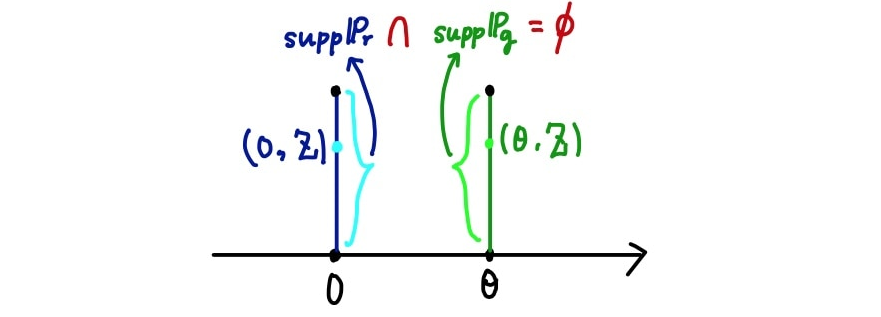
두 분포가 위와 같이 나타난다면(즉, $\mathbb{P}_r$과 $\mathbb{P}_g$가 안 겹친다면) KL & JS 발산의 값이 어떻게 될까?

즉, $\theta\ne0$인 경우 아래와 같은 식이 성립한다.

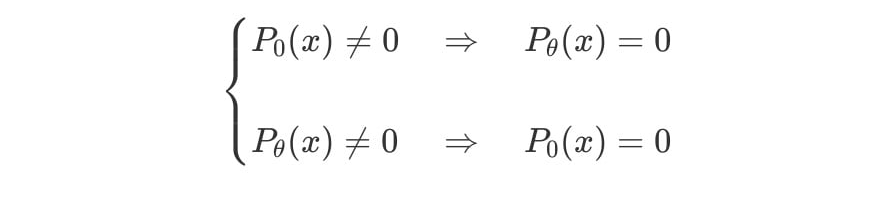
따라서, $P_{\theta}(x)>0$인 곳에서 $log \ P_0(x)$의 값은 0이 된다.

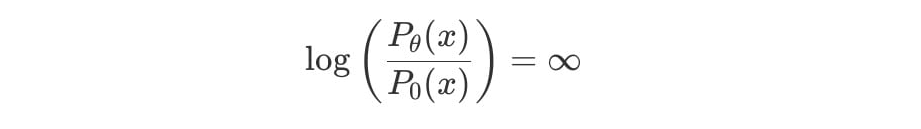
그러므로 $P_{\theta}(x)>0$인 곳에서 KL발산 값은 아래와 같이 무한대로 발산한다.

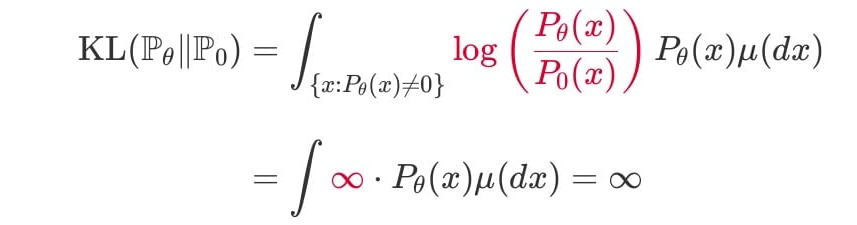
다시 말하면, $\theta=0$ 이 성립하지 않는다면, (위의 분포처럼 겹치지 않는 점에 대해) KL발산이 무한대로 발산하는 것.

위에 오타 있다.

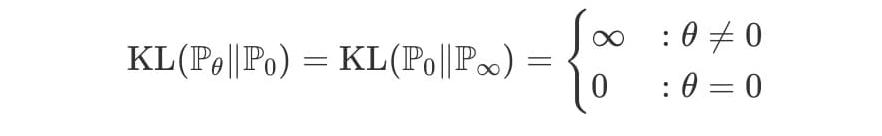
마찬가지로 JS발산 또한 아래와 같이 구할 수 있다.

식에 대입만 하면 쉽게 구할 수 있으며, 적분 구간에서 $P_0\ne0$, $P_{\theta}\ne0$인 이유는 $P_0=0, P_{\theta}=0$일 경우 어차피 피적분함수가 0이되기 때문에 생략한 것.

JS발산는 무한대로 발산하지는 않으나, 역시 log2로 상수 값만을 가지기 때문에 좋은 피드백을 주기는 쉽지 않다.

이처럼 TV, KL, JS 발산은 모두 두 확률분포가 서로 다른 영역에서 측정된 경우 완전히 다르다고 판단을 내리게끔 metric이 정의됐기 때문에 위와 같은 일들(TV=$1$, KL=$\infty$, JS=$log 2$)이 일어난다. 거리를 굉장히 harsh하게 따지는 것.

상황에 따라 잘 작동할 때도 있겠지만, GAN에서는 판별자(discriminator)의 학습이 잘 죽는 이유(Gradient Vanishing)가 되기도 하기에 조심스럽게 다룰 필요가 있다.

---

KL&JS 발산과 TV distance의 관계

(출처 : Wasserstein GAN 수학 이해하기 I(임성빈))

---

4. Earth-Mover distance of Wasserstein

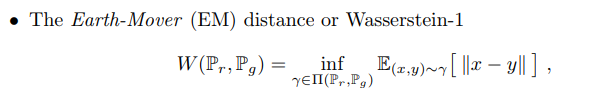
• Earth-Mover distance는 다른 3개의 Distance(TV, KL, JS) 과는 다르게 어떤 분포든 간에 일정한 추이를 보이는 특징이 있습니다. TV, KL, JS의 경우 모수에 따라 거리가 달라질 수 있으며, 두 분포가 겹친다면 0, 아예 안 겹친다면 무한대(or상수)로 극단적인 값을 가져 그래디언트가 잘 전달되지 않을 수 있습니다.