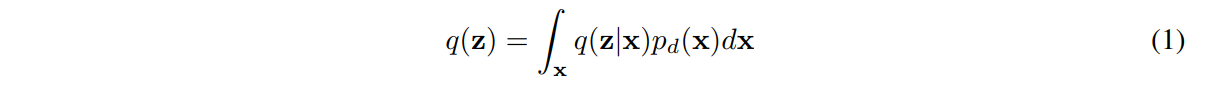
Paper : Adversarial Autoencoders

본 글은 AutoEncoder(혹은 Variatioanl Auto Encoder) 내용을 기반으로 하기 때문에 이에 대한 지식이 선행되어야 합니다.

Approach-to-VAE(2) <-- 본 블로그 내 정리 글을 참고하세요 !

---

0. Abstract

---

Adversarial Auto Encoder(AAE)는 Variational Inference를 수행하기 위해 GAN을 사용하는 확률적 오토인코더입니다. 구체적으로 말하자면, hidden code vector의 aggregated posterior를 임의의 prior distribution과 매칭하여 변분추론(Variational Inference)를 수행합니다. 이 때 aggregated posterior를 prior에 매칭시키는 것은, prior space의 특정 영역에서 샘플을 생성할 때 의미 있는 샘플을 생성하는 것을 보장합니다. 이에 따라 AAE의 decoder는 가정한 prior를 data 분포로 매핑하는 Deep generative model을 학습합니다.

AAE는 Semi-supervised classification, Disentanling style and content of images, 비지도 클러스터링, 차원 축소(-> 데이터시각화) 등과 같은 분야에 널리 사용될 수 있습니다.
Evaluation은 MNIST, Street View House Numbers, Toronto Face dataset에 대해 생성모델링, semi-supervised 분류 등을 진행하였습니다.

1. Introduction

음성, 이미지, 비디오처럼 고차원적이고 풍부한 분포를 포착하는 생성모델을 만드는 것은 머신러닝의 주요 과제 중 하나입니다. 이전까지, 규제 볼츠만 머신(RBM), Deep Belief Networks(DBNs), Deep Boltzmann Machines (DBMs) 등과 같은 Deep generative model들은 주로 MCMC(마르코프 체인 몬테 카를로) 기반 알고리즘으로 학습되어 왔습니다. 이러한 접근법을 택하게 되면 학습이 진행됨에 따라 제한적인 log likelihood의 그래디언트를 계산하기 때문에 한계가 존재합니다.

반면, 최근에 개발된 Variational Autoencoder(VAE), Generative Adversarial Network(GAN), Generative moment matching networks(GMMN) 등 direct back-propagation을 통해 학습하는 생성모델들은 이러한 한계들을 훌륭하게 보완했습니다.

VAE : 잠재 변수에 대한 사후 분포를 가정하고 이에 대한 parameter를 추론하는 네트워크(변분추론 - Variational Inference).
GAN : 따로 분포에 대한 가정을 하지 않고 데이터 분포로부터 네트워크의 output distribution을 직접적으로 형성.
GMMN : 데이터 분포를 학습하기 위해 moment matching cost function 사용.

---

2. Method

글의 구조는 본 논문과 다를 수 있습니다.

Architecture

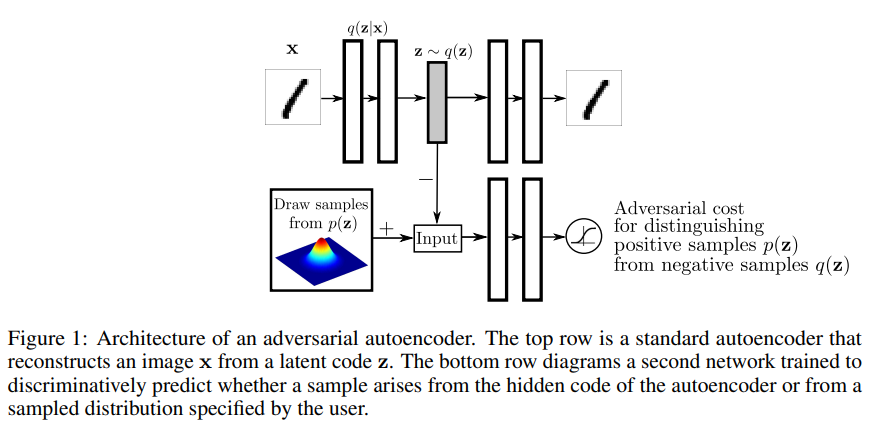
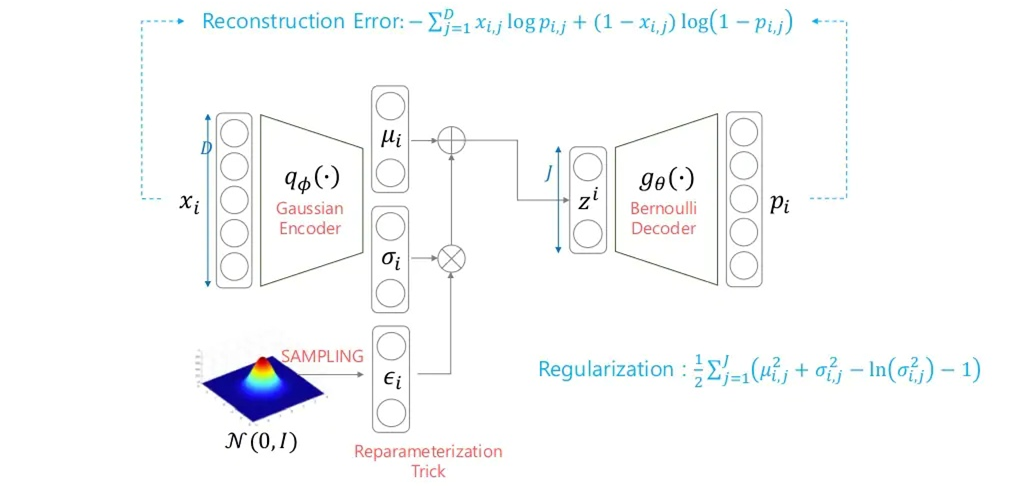
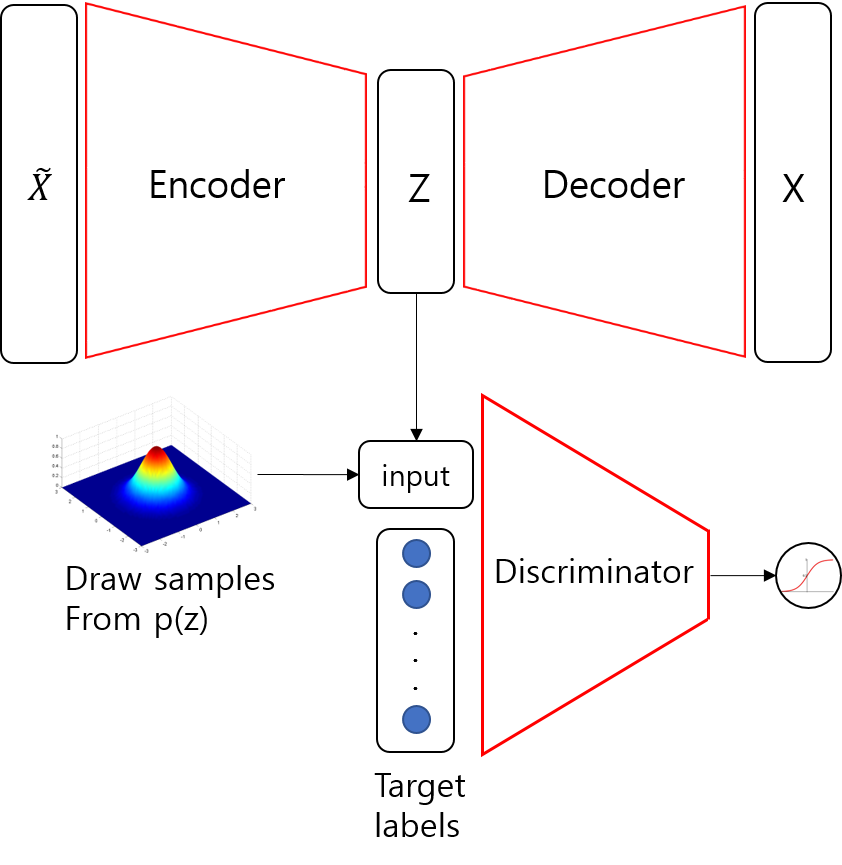
Adversarial Auto Encoder의 구조는 위와 같습니다.

윗단은 일반적인 AutoEncoder로, 이미지 $x$를 받아 reconstructed image를 복원하게 됩니다.
아랫단은 새로운 Discriminator가 Encoded latent vector distribution인 $q(z)$와 random sample $p(z)$을 구분하게 됩니다.

즉, $z$가 오토 인코더의 인코딩과정을 거쳐서 얻은 parameter distribution $q(z)$에서 나온 것인지, 아니면 사용자가 직접 정의한 distribution에서 나온 것인지 구별합니다.

그러면, 오토 인코더는 사용자가 정의한 $p(z)$ 가까워지게끔 $q(z)$를 학습하겠죠?
그러면 다루기가 아주 쉬워질 것입니다.

Training

1. Reconstruction phase(AE)

AE와 동일하게 Encoder와 Decoder를 학습하는 단계입니다.

Adversarial Auto Encoder

2. Regularization phase(Adversarial networks)

Adversarial Auto Encoder의 latent vector $z$를 학습하는 단계입니다.

Adversarial Auto Encoder

1. $p(z)$와 $q(z)$를 구분할 수 있도록 discriminator 학습
2. $p(z)$와 $q(z)$를 구분할 수 없도록 generator 학습

Three types of Encoder q(z|x)

본 논문에서는 Encoder $q(z|x)$로 세 가지 종류를 제안합니다.

VAE의 그림은 참고로 봅시다(본 그림은 NAVER D2 '오토인코더의 모든 것' 강의에서 발췌하였습니다).

그 전에 앞서서 , 본 논문은 아래의 식 $q(z)$를 aggregated posterior distribution이라 정의합니다.



대충 '데이터의 분포와 모델의 분포가 모두 담겨있는 사후분포' 정도로 받아들이면 될 것 같습니다.

(1) Deterministic

$q(z|x)$를 $x$에 대한 deterministic function으로 가정합니다.

즉, 이 경우 데이터 분포 $p_d(x)$를 통해서만 $q(z)$의 stochasticity(확률성)를 얻습니다.

• 뭐 사실상 오토인코더는 데이터에 의해서만 학습된다고 봐도 무방하겠죠.

(2) Gaussian posterior

$q(z|x)$가 가우시안을 따른다고 가정합니다.

이 때에는 (a) 데이터 분포 $p_d(x)$와 더불어 (b) encoder 내 output에서의 가우시안 분포로부터 $q(z)$의 stochasticity를 얻습니다.

• VAE와 마찬가지로 reparameterization trick을 사용해야 합니다.

(3) Universal approximator posterior

encoder가 $x$와 노이즈 $n$을 input으로 받는 함수 $f(x,n)$라 가정합니다.

이 때에는 $q(z)$가 데이터 분포 $p_d(x)$와 노이즈 $n$으로부터 stochasticity를 얻습니다.

• 노이즈는 가우시안 등의 고정된 분포에서 추출합니다.

여러 노이즈 $n$을 샘플링해 추출한 다음, 임의의 사후 분포 $q(z|x)$를 구할 수 있게 됩니다.

이에 대해서는 아래와 같이 주변확률분포를 이용해 전개할 수 있습니다.

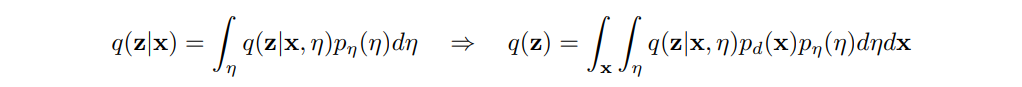
이렇게 정의한다면 '(2) Gaussian posterior'처럼 사후 분포 $q(z|x)$는 굳이 Gaussian일 필요가 없고 그냥 Input data $x\in X$들이 주어졌을 때 임의의 사후분포를 학습할 수 있습니다.

특히, 이 경우 $q(z)$로부터 $z$를 손쉽게 얻을 수 있는 방법을 사용하기 때문에 판별자로 인해 $q(z)$가 $p(z)$에 가까워지게 됩니다.

• 더 정확히는, Encoder 내에서 Back-propagation을 진행함으로써 학습됩니다.

---

위와 같이 Encoder의 각기 사후분포를 가정함에 따라 결과도 당연히 다양합니다.

가령,

(1) Deterministic Encoder를 사용할 경우 사실상 데이터 셋에 의해서만 분포가 결정이 되고, 데이터 셋의 경우 사실상 고정되어 있기 때문에 $q(z)$는 부드럽지 못할 것입니다.

반면,
(2), (3)의 경우 특정 "분포"에서도 확률성이 주어지기 때문에 (Adversarial) Regularization 단계에서 $q(z)$를 부드럽게 형성하게 됩니다.

근데 실질적인 성능(test-likelihood)차이는 안 나서 예시들도 그냥 Deterministic Encoder로만 게재했다고 하네요..

AAE vs VAE

---

VAE에서는, KL-divergence(분포 간 차이)이 인코딩된 잠재 분포 $q(z|x)$ (사전) 정규분포로 일치시키는 데 사용됩니다.
반면, AAE에서는, hidden code vector의 aggregated posterior 분포 $q(z)$를 prior에 맞추도록 학습해 비슷한 효과를 냅니다.

즉, 우리가 원하는 posterior distribution을 prior distribution과 가깝게 하기 위해 VAE는 KL-발산을, AAE는 GAN을 사용한 것입니다.

이 과정에서, VAE는 monte carlo를 통해 KL 발산 계산식이 필요하기 때문에 prior를 정확히 어떤 함수로 정의해야 합니다.

즉, VAE는 Explicit density를 가정합니다(보통 가우시안).

반면, AAE는 prior를 특정 함수로 정의하지 않고 단순히 샘플링만 가능하면 됩니다. 즉, AAE는 Implicit density를 가정합니다.

실질적으로 GAN의 Implicit density 성질을 이용해 VAE의 Explicit density한 성질을 잘 보완(?)했다고 볼 수 있습니다.

---