본 글은 주로 Woong won, Lee님의 gitbook과 sumniya님의 블로그를 주로 참고했습니다.

Planning by Dynamic Programming

1. Introduction

Dynamic programming(DP) 은 본래 강화학습에 쓰이는 용어가 아니다. 일반적으로 시간에 따라 변하는 문제를 다양하게 쪼개서 풀어야 할 때 DP가 사용되곤 한다. 하지만, DP를 강화학습 태스크에 적용하기 위해서는 문제를 알아야 하고, 강화학습 태스크에서의 문제는 Environment(State, Reward 등)을 알아야 정의할 수 있다. 즉, Model-based 방법인 것. 이의 대척점에는 Model-free method가 놓인다. 즉, 전자는 Planning, 후자는 (Reinforcement) Learning이라고 할 수 있다.

본 글에서는 Dynamic Programming, Monte Carlo Methods, Temporal-Difference Learning에 대해서 간략하게 다룰 것이다.

Dynamic Programming : 수리적으로 잘 구축되나, 완벽하고 정확한 (environment)의 모델을 알아야 한다.
Monte Carlo Methods : 모델을 필요로 하지 않고 개념적으로 간단하다. 하지만, step-by-step으로 증가하는(incremental) 연산에는 맞지 않다.
Temporal-difference learning : 역시 모델을 필요로 하지 않으며 완전히 incremental하다. 하지만 분석하기 너무 복잡하다.

위의 세 모델은 연산량, 효율성 등의 관점에서 장단점을 갖는 것을 알 수 있다.

즉, DP는 Planning의 한 방법으로 MDP 문제에서 environment의 모델을 완벽하게 안다는 전제 하에 Optimal policies를 연산하는 데 쓰이는(즉, 벨만 방정식을 푸는) 알고리즘들의 총체라 할 수 있다.

Dynamic Programming은 planning에 해당해, environment의 모델을 모두 안다는 가정하에 문제를 푸는 방법이다. 엄연히 따지면 강화학습은 아니지만, 이를 토대로 발전한 것이 RL이기 때문에 DP를 이해하는 것도 중요하다.

2. Polity iteration

Prediction & Control

DP는 (1) Prediction (2) Control 두 단계로 나뉜다.

Prediction : 현재 optimal하지 않은 policy에 대해 value function을 구한다.
Control : 현재 value function을 토대로 더 나은 policy를 구한다.

어딘가 익숙하지 않은가?

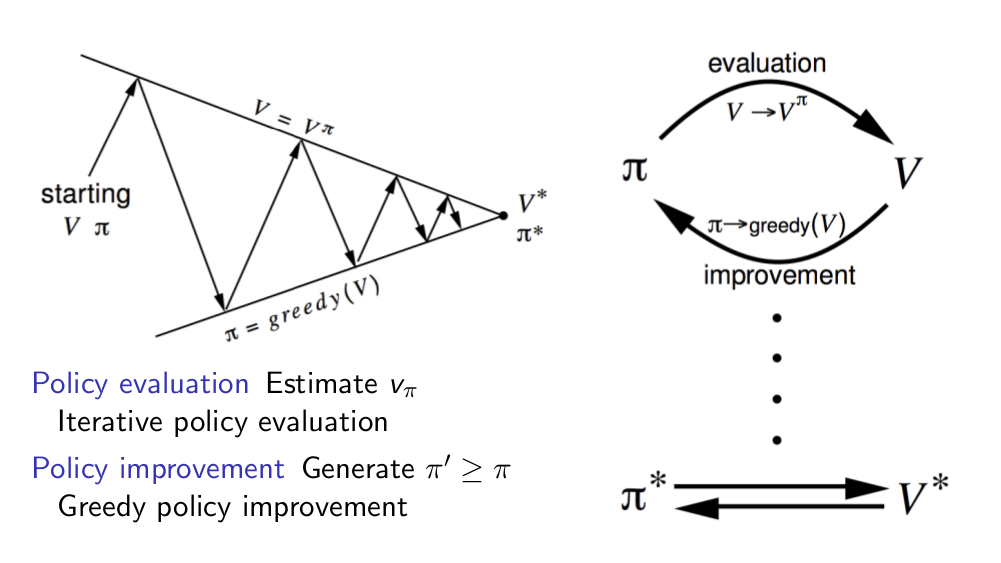
Policy Evaluation

• policy를 평가한다는 것은 어떤 policy를 따라갔을 때 Return을 얼마나 받는지 알면 된다. 이 말은, value function을 알면 된다는 말이다. 이를 위해 synchronous backups방법을 사용한다.
  

최종적으로 우리가 찾고자 하는 것은 각 state들의 true value function $v_{\pi}(s)$이다.

true value function
최초의 policy는 random 상태로 시작한다. 현재 따르기로 한 policy가 옳은지, 그른지 판단해가며 이를 발전시켜야 하는데, 문제는 policy에 따라 각 state의 중요도가 다르고, agent는 이를 모른다는 것이다. 그렇기 때문에 agent는 여러 state를 넘나들며 value function을 update해 최종적으로 어떤 state가 중요한 지 판단할 수 있게끔 하는 것이다. 당연하게도 문제의 복잡도 측면에서 이 true value function을 바로 구할 순 없기 때문에 iteration을 통해 점점 true value에 도달하고자 하는 것.

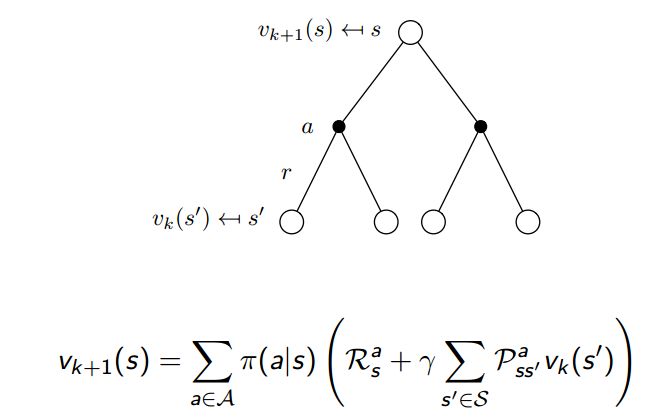
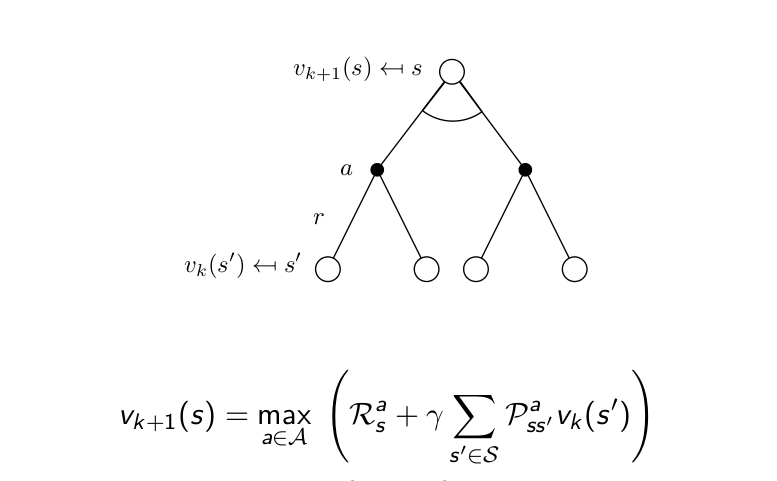
이때 하나의 iteration에는 우리가 알고 있는 모델을 이용해서 전체 state의 value function을 모두 구합니다. 당연하게도 value function은 벨만방정식을 통해 구합니다!

즉, 위처럼 true value function을 구하기 위해 iteration을 반복하는 것을 policy evaluation이라 한다.

즉, 전체 MDP의 모든 state에 대해 동시에 한 번씩 벨만방정식을 계산해서 update하고, $k$를 한 단계 올린다.

이 때, 현재의 state인 $s$의 (k+1)번 째 value function은 $s$에서 이동가능한 $s'$에 대해 $k$ 번째에서 구해 놓은 value function을 이용한다.
즉, neighborhood(가칭)-state value function으로 present-state value function을 구하는 것을 Back-up이라고 표현합니다.
이 step에 따라 one-step bakcup과 multi-step backup으로 나뉘고, 구하는 state의 종류에 따라 full-width backup과 sample backup으로 나뉩니다.
역시 예시로 한 번 살펴보자.

• Deternimistic한 environment이기에 state transition probability는 1이다.
• ternimal state는 위 그림에서 회색 그리드에 해당한다.
• 그리드를 벗어날 경우 제 자리로 다시 돌아온다.
• discount factor는 설정하지 않는다($\gamma=1$).
• Reward는 이동 시 -1이다.
• policy는 동서남북 모두 random하게 움직이는 policy로 정의한다.

이 경우, value function을 구해보자.

이하 그림 출처 : https://sumniya.tistory.com/10

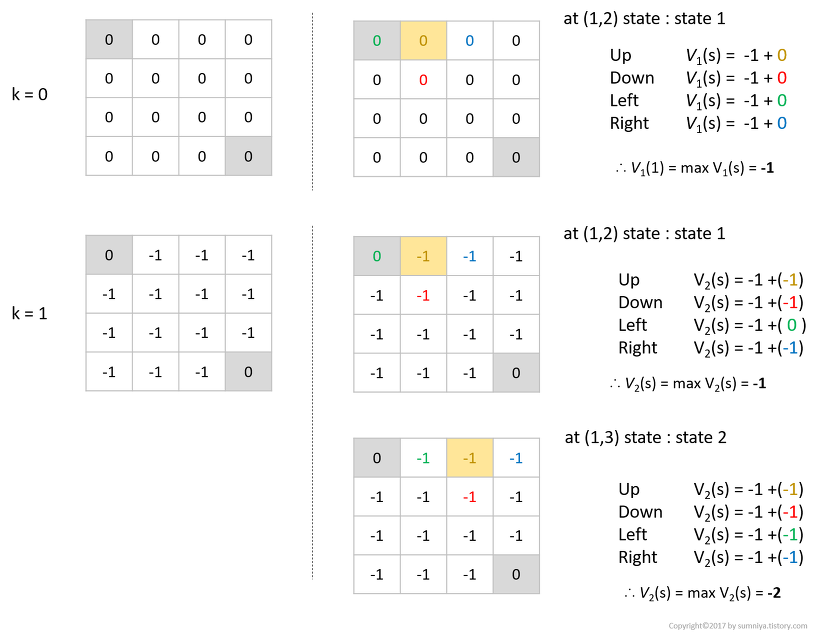
iteration 0

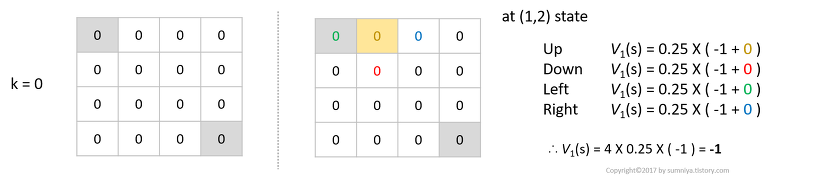
• 초기의 value function은 0이다.
• 위 그림에서 위치 (1,2)의 iter 1 value function은 위치 (1,1), (1,3), (2,2), (1,2)(제자리)의 iter 0 value function을 통해 구할 수 있다.

iteration 1

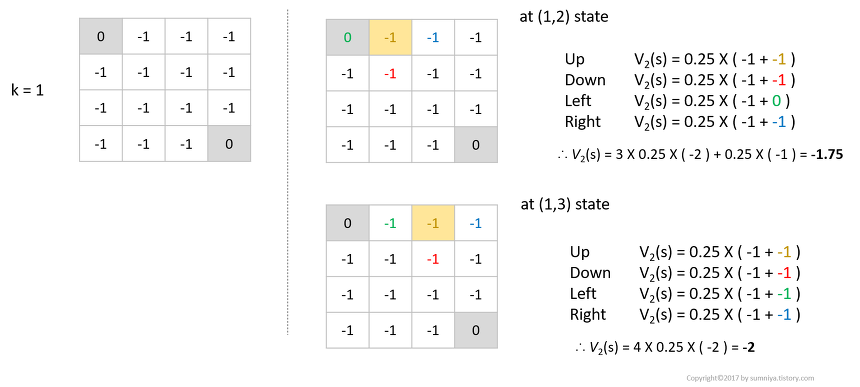
• iteration 0때와같은 방식으로 state (1,2), (1,3)의 value function을 구할 수 있다.

위처럼, 발상 자체는 그렇게 어렵지 않다. 하지만, 실제 상황에서 DP의 계산량은 과도하게 많으며 정의 상 model을 알아야 풀 수 있기에 DP의 단점은 꽤나 극명하 편이다. 그렇기에, 이를 강화학습(RL)로 보완하려는 게 현재의 흐름이다.

Policy Improvement

우리는 (policy를 random move라고 가정한 채)위의 Policy Evaluation을 거쳐 true value function을 찾았다. 그러면 이를 토대로 현재의 policy보다 더 나은 optimal policy를 찾아야 한다.

policy evaluation 단계에서 state-value function을 통해 각 state에 대한 value 값을 구했으므로, 이제는 policy에 따른 action을 고려한 value 값을 따라 action을 취해야 한다.

위와 같은 상황을 고려해, 컴퓨터가 이해할 수 있게끔 정량화 작업을 거쳐 기준을 만드는 것이 바로 q-function(action-value function) 이다.

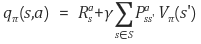
위의 q-function에서 $R^{a}_s$의 역할은 이전 글 참고

즉,

policy evaluation : state의 value function을 iterative하게 계산해 모든 state의 true value를 도출하는 방법
policy improvement : 도출된 state value를 토대로 현재의 policy를 action-value를 이용하여 better policy를 선택하는 방법.

이 때, 가장 간단한 policy 개선 방법인 Greedy policy improvement을 생각해보자.

이름에서 눈치 챘겠지만, 그냥 가치(value)가 높은 state를 따라서 이동하는 방법입니다.

이 greedy policy의 경우가 바로 위의 q-function을 max function으로 바라보는 상황인 것이다.

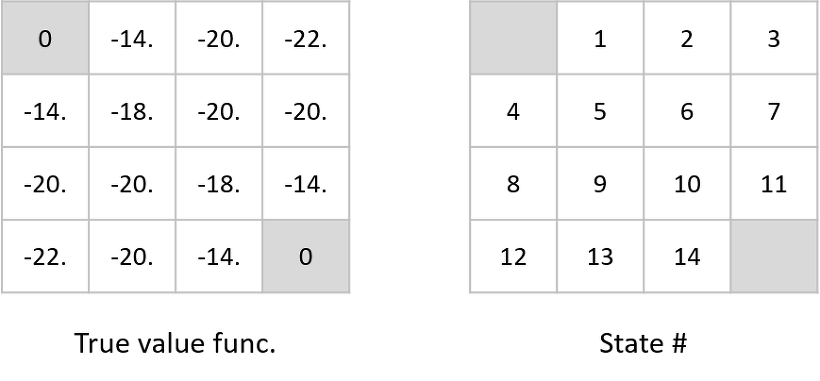
위의 그림에서 왼쪽 그리드는 true value function, 오른쪽 그리드는 단순히 state notation이라 하자.
이 때, state 1과 state 5에 대한 q-function을 구하면 아래와 같다.

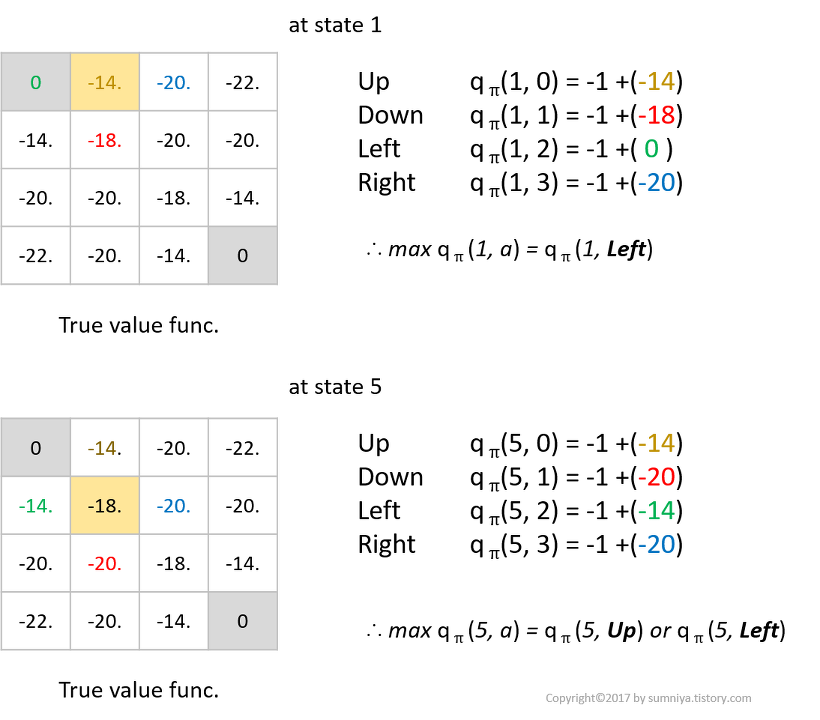
이 과정을 통해 모든 state의 policy improvement를 계산하면 아래 그림과 같다.

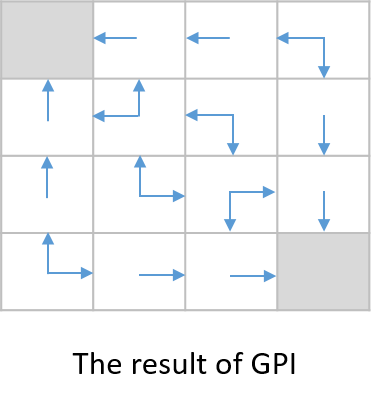
위의 예시는 너무나도 간단하기에 policy evaluation 한 번, policy improvement 한 번만 진행하면 optimal policy를 찾을 수 있게 된다. 다만, 보통은 위의 과정을 계속해 반복 수행해야 최적의 해를 얻을 수 있게 된다.

Policy iteration

Value iteration

Value iteration은 Bellman Optimality 방정식을 이용하여 evaluation을 한 번만 진행하는 방식이다. 기존의 Policy iteration에서는 evaluation 과정에서 이동 가능한 모든 state $s'$에 대한 value function 값을 더하여 도출했었다. value iteration에서는 이렇게 더하지 말고 구한 value function 값들 중 max 값에 해당하는 value function만을 구해 improve하자는 게 핵심 아이디어이다.

즉, 한 번의 evaluation + improvement = value iteration

앞에서 진행했던 예제를 그대로 사용해 Value iteration을 사용해보자.

기존에는 random policy를 시작으로 evaluation을 진행했었다.

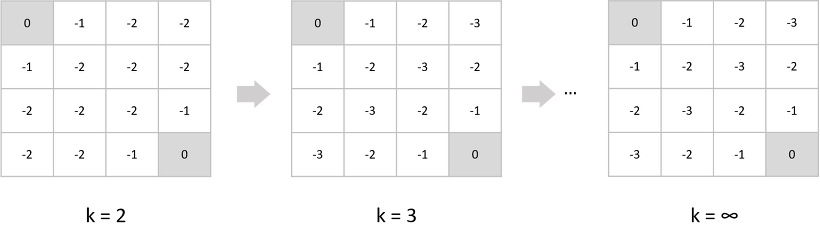
위의 그림은 value iteration의 반복 횟수가 늘어남에 따라 변하는 각 state의 value function이다. 보다시피 iteration이 (k=3)일 때 이미 수렴한 것을 볼 수 있다.

Policy Iteration vs Value Iteration

Policy Iteration

• policy에 따라 value function이 확률에 따라 주어진다(즉, Bellman Expectation 방정식을 사용한다).

Value Iteration

• 현재의 policy가 optimal하다는 것을 전제로 value function의 max를 취하므로, 결정적으로 주어진다(즉, Bellman Optimality 방정식을 사용한다.

Value iteration 과정에서는 evaluation 단계에 사실상 optimal한 policy를 결정하는 improvement 또한 내재되어 있다고 생각하면 편합니다.

결론적으로, Dynamic Programming의 두 가지 iteration 방법을 소개했습니다. 이 경우 model을 알아야한다는 제약은 물론이고, 계산량이 너무나도 방대하다는 단점이 있습니다.
이를 보완하기 위헤서 full-width backup(가능한 모든 state $s'$에 대해 연산하는 것) 대신 sample bakcup을 사용하는 방법이 있습니다.

Sample Backup

위처럼 Dynamic programming은 연산량, 모델 인지 등 치명적인 단점이 있었다. DP를 full-width backup을 통해 구하게 된다면 단 한 번의 backup만으로도 굉장히 많은 연산량이 요구된다. 특히, state 숫자가 큰 경우에는 사실상 불가능한 업데이트 방법이라 할 수 있다. MDP에 대해서 다 알지 못할 때는 아예 불가능 한 것은 당연하다.

DP

• MDP의 Transitions matrix와 reward function을 알아야 한다.
• state 변수의 개수에 따라 $\mathcal{S}$는 지수적으로 증가한다.
• DP는 적당한 size(여기선 100만개 정도)의 problem에만 권장된다.

Sample back-up

• 가능한 모든 (뒤따르는)state를 고려하는 게 아닌, sampling을 통해 한 길만 가보고 그를 토대로 value function을 업데이트 하는 것.
• 결과를 토대로 업데이트를 실행하므로 model-free가 가능하다.
  - $<S,A,R,S'>$를 토대로 나온 reward와 sample transition만 이용하면 된다.
• 즉, model을 몰라도 optimal policy를 구할 수 있는 Learning이 가능한 것.
• 상태들의 개수인 $n=|\mathcal{S}|$와는 독립적이다.

이 Sample backup에는 후에 다룰 Monte-Carlo methods와 Temporal Difference Model이 대표적이라 할 수 있습니다.

Refenrence

https://sumniya.tistory.com/10?category=781573
https://dnddnjs.gitbooks.io/rl/content/policy_iteration.html