본 글에서는 강화학습의 핵심인 Markov Decision Processes(MDPs)를 다룬다.
- Intro to RL 에서도 Markov Property에 대해 다루었습니다.
1. Markov Processes
Introduction

Markov decision process(MDPs)는 일반적으로 강화학습에 쓰이는 Environment를 기술한다고 볼 수 있다. 이 때, Environment는 agent가 관측할 수 있는 상황인 fully observable environment를 가정한다. 즉, 현재 state가 process를 완전히 표현할 수 있는 상황이다.
이 때, 모든 강화학습 문제는 MDPs형태로 치환할 수 있다.
가령, 최적의 제어 문제는 연속적인 MDPs를 다룬다 볼 수 있고, 부분적으로 관측가능한 문제도 MDPs로 치환할 수 있으며, 슬롯머신 문제는 one state를 가진 MDPs로 여길 수 있다.
Markov Property

"현재가 주어졌을 때, 미래를 알기 위해서 과거는 다 버릴 수 있다"
이 말을 수식으로 표현하면 위의 Definition과 같다.
현재의 state는 history로부터 모든 정보를 포착할 수 있고, 그렇기에 state만 주어진다면 history는 버릴 수 있다.
즉, state는 future를 기술하기 위해 충분통계량이다.
State Transition Matrix
우선, 가능한 state는 개로 이루어져 있고, discrete하게 다른 state로 전이할 수 있는 Markov process라 가정해봅시다.

이 때, State Transition Matrix는 시간 일 때 state 에 있다면, 다른 state들에 전이할 확률들을 담은 행렬이다. 즉, Environment를 설명하는데 필요한 요소들이라 할 수 있다. 이 때, 각 행의 합은 당연히 1이 될 것이다.
Markov Chains
Markov Process는 시간에 상관 없이 랜덤하게 다른 state로 전이할 수 있는 process라 할 수 있다. 즉, Markov property를 갖는 random states 의 sequence이다. 이 때, Markov process는 와 로 정의할 수 있다. 즉, 전이할 수 있는 state 집합 과, 그 state 간의 전이 확률을 담은 전이 확률 행렬 만 있으면 완전히 정의된다.
즉, state 개수를 이라 할 때, 개의 확률과 개의 state만 있으면 Markov Process는 하나로 정해진다.
state transition matrix는 특정 조건들을 만족하면 (...)하다고 한다. (...)할 때는, 예를 들어, 1억명을 각 state에 맞게 퍼뜨리는 상황을 고려해보자. 이 때, 충분한 수의 전이를 거치면 각 state에 위치하는 사람의 분포는 균등하다 할 수 있다.
이 때, random process라는 말은, sampling을 진행할 수 있는 말과도 같다.
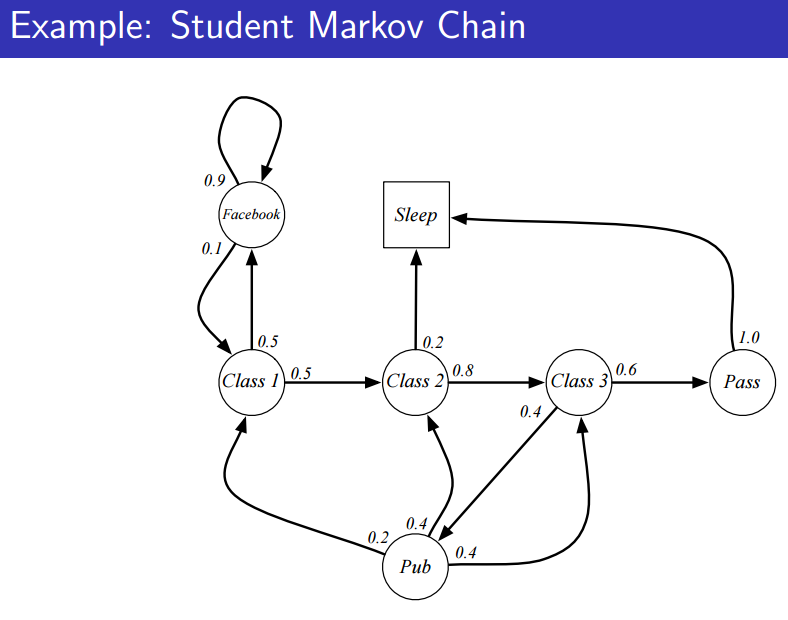
위에 그림에 따르면 state가 7개 있고, 화살표에는 전이 확률이 나타나 있다.
이 때, Terminal state란 종점, 즉 에피소드가 끝나는 state를 가리킨다.

에피소드를 샘플링한다는 얘기가 많이 나온다.
샘플링은 강화학습에 많이 나오는 요소기 때문에 익숙해질 필요가 으며, 당연하게도 에피소드 sequence는 거의 무한한 경우의 수가 될 것이다.
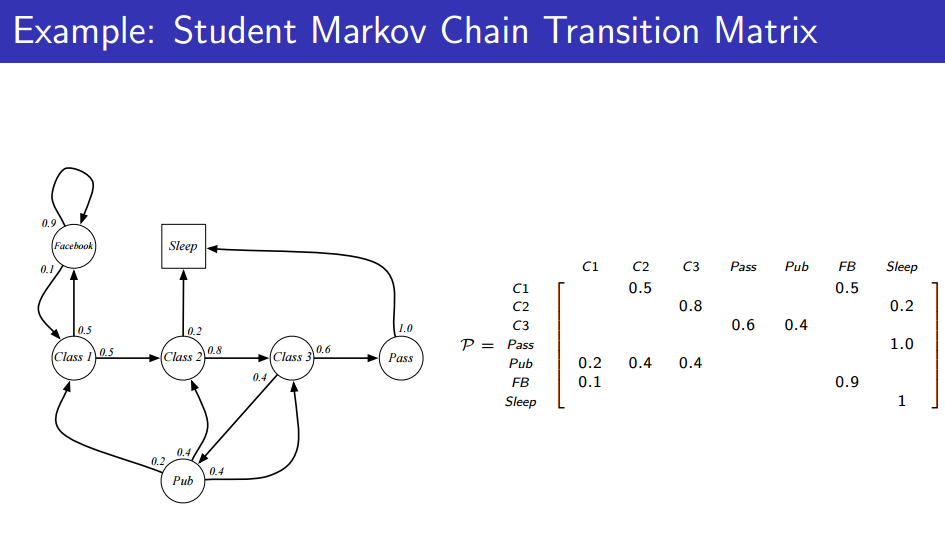
여기서 state와 전이 확률들을 담은 Transition matrix를 정의할 수 있게 된다. 그러면, node와 edge로 그림을 그리지 않더라도 사실상 Transition matrix가 모든 정보를 표현하는 것을 볼 수 있다.
2. Markov Reward Process(MRP)
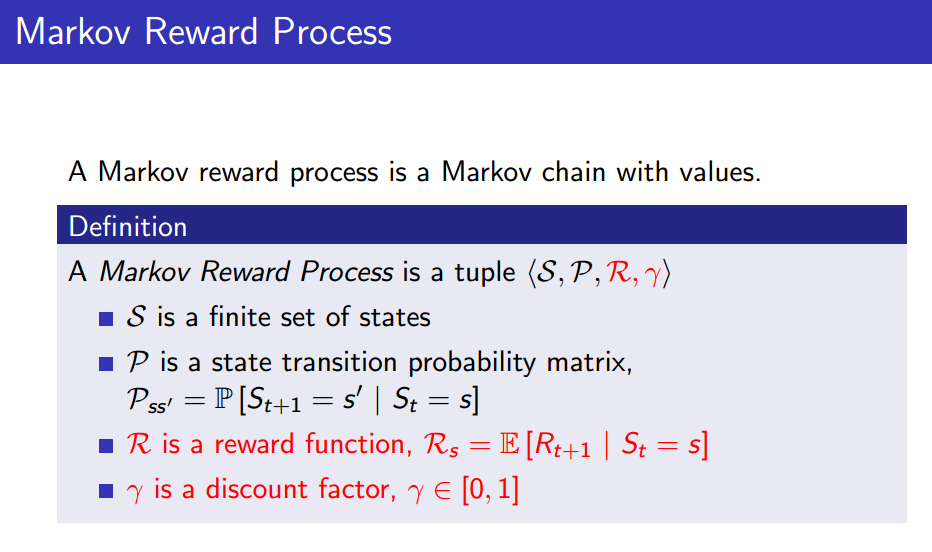
MRP
Markov Process란, Environment의 dynamics에 관한 것으로 볼 수 있다. 가 주어진다면 Markov Process가 정의된다 할 수 있는데, Markov Reward Process는 무엇일까?
위처럼 가 주어진다면 Markov Reward Process가 정해진다고 할 수 있다.
이 때, 은 state 별로 reward를 정해주는 함수이고, 은 state의 timestep에 따라 감쇄율을 정해주는 discount factor이다.
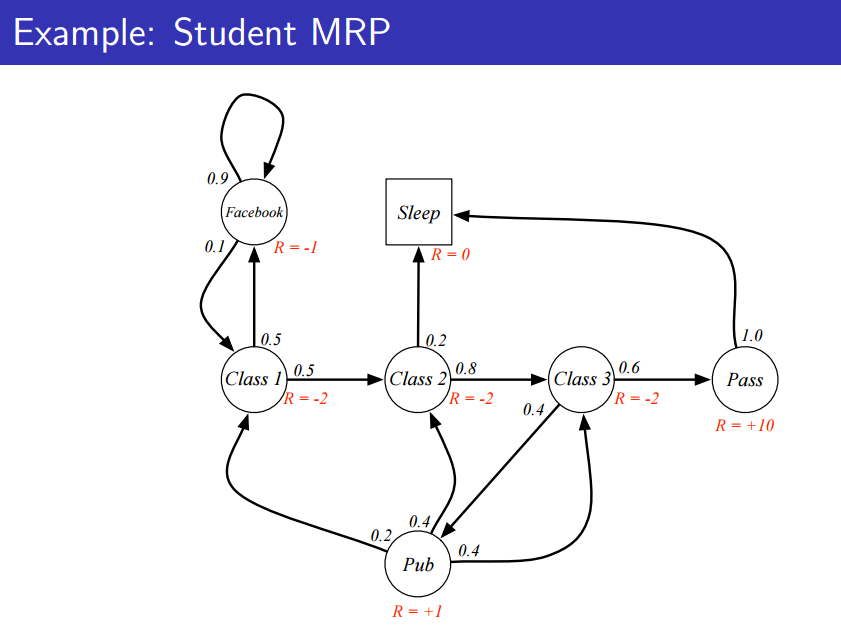
위의 그림을 보면 Reward는 나름 합리적으로 정의했다는 것을 볼 수 있다(페북, 공부, 잠).
이 때, Reward Process에는 Action이란 게 없습니다. 단지 확률에 따른 state가 정해지기 때문에 action이 아닌 state에만 reward가 주어지면 되는 것입니다.
뒤에 나올 MDP(Markov Decision Process)에서는 Action과 State 모두에게 Reward가 주어집니다.
Return

다시 한 번 말하지만, 강화학습이란 Return을 최대화 하는 문제이다. 정확히는, 미래에 받을 Reward의 '총합'을 최대화 하는 게 강화학습이였다.
즉, 에피소드를 sampling할 수 있다 가정할 때, 각각의 에피소드를 따라 받는 Reward의 총합이 Return인 것이다.
이 때, 에피소드의 reward들을 단순히 더하는 게 아닌, 미래의 reward는 discount factor만큼 곱해줌으로써 영향력을 낮춰줌으로써 총합을 구한다.
감마가 0에 가까울 수록 미래의 reward은 없애니 'myopic'(근시안적)이라 하고, ... 감마가 1에 가까울 수록 미래의 reward를 더욱 고려하기 때문에 'far-sighted' 라고 할 수 있습니다.

그렇다면, Discount를 꼭 해야할까? 미래를 더욱 고려해야 하는 것 아닌가?
Discount를 하는 이유를 몇 가지 고르자면 아래와 같다.
- 수학적으로 편리하다(수렴성을 증명할 수 있다).
- 미래에 대한 불확실성은 때때로 완전히 표현되기 어렵다.
- 경제적인 관점의 reward라면 당연히 즉각적인 reward를 선호할 것이다.
- 그냥 인간은 즉각적인 reward를 원한다.
- 모든 sequnece가 끝나는 게 보장되는 환경이라면 discount를 하지 않아도 계산할 수는 있을 것이다.
아무튼, 문제에 따라도 사용을 할 수도 있긴 하나, discount를 하는 경향이 크다는 것이다.
Value Function

(state) value function은 한 마디로 state 가 주어졌을 때 'return()의 기댓값' 이라 할 수 있다. 즉, MRP에서 value function은 어떤 state에 도착했을 때 샘플링을 통해 에피소드를 만들어 나가는데, 그 샘플링된 에피소드들을 이용해 평균적으로 Return 값을 구할 수 있는 것이다.
의 기댓값(Expentation)을 value function으로 정의한다는 사실로부터 는 확률변수임을 알 수 있다.

위의 그림을 보면 한 눈에 이해할 수 있다. 이 때, 샘플링을 할 때 이미 확률에 대한 요소가 들어가기 때문에 나온 Return 값들을 단순하게 평균내주면 된다.
Policy 또한 여기선 언급하고 있지 않지만, 보통 state 에서 policy를 따라 에피소드가 생성되는 것을 기억하자.
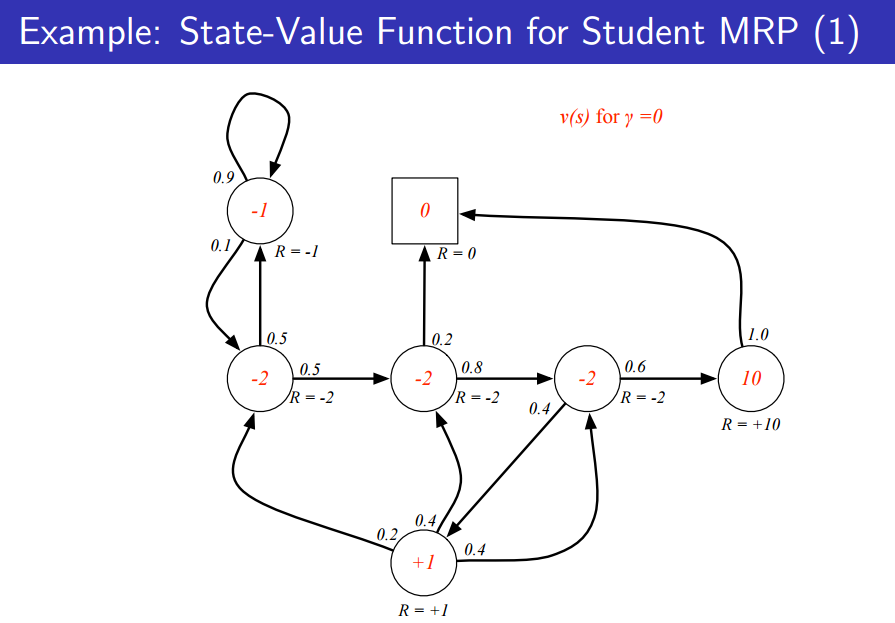
위의 그림은 discount factor가 0이라 가정하고, state value function(빨간 숫자)을 구한 그림이다. 미래는 고려하지 않기 때문에 값이 Reward랑 같다는 것을 알 수 있다.
아래처럼 discount factor를 변경시킨다면 state value function 또한 변하는 것을 알 수 있다.
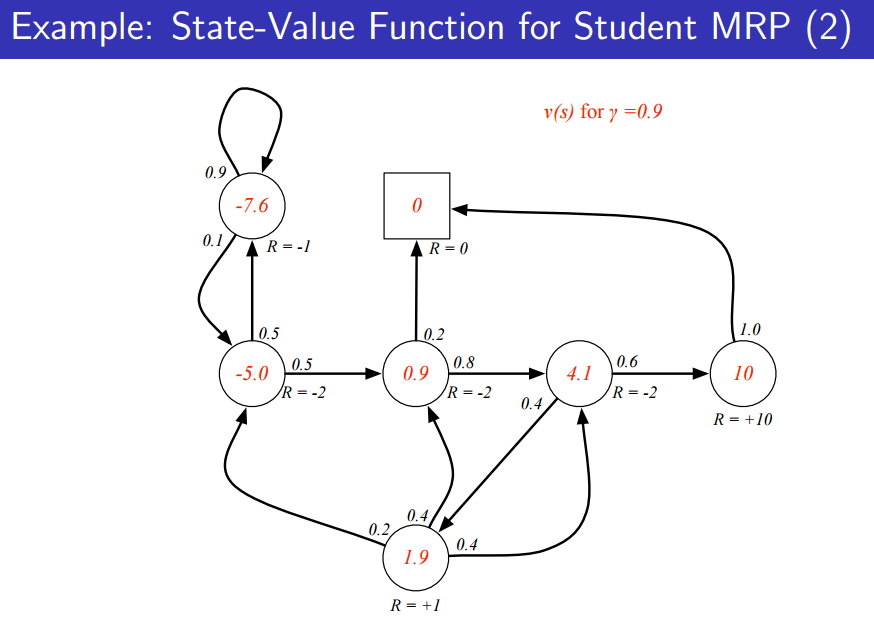
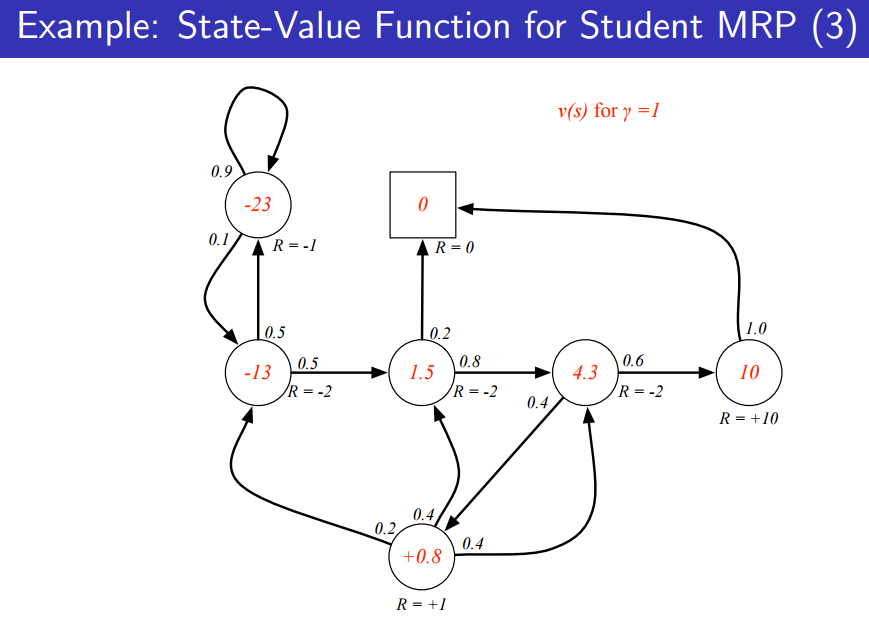
구하는 방법은 위에서 언급한 sampling을 이용해 구할 수도 있지만, 후에 다른 방법을 구할 것이다.
Bellman Equation

value-based method에서는 value function을 지배하는 방정식이 Bellman Equation이라 할 수 있다.
즉, iterative한 방법으로 학습이 진행된다.
식은 굉장히 쉽습니다. Expectation은 식 안으로 들어갈 수 있습니다.
즉, 는 과 어떤 관계를 갖는 것을 알 수 있습니다.
&어떻게 조건부 를 무시할 수 있는지?

그림으로 살펴보자. 현재 state 에서 다른 state로 갈 수 있는 많은 경우의 수가 존재한다. 각각 state로 전이할 확률이 정의되어 있기에(MRP) 그 확률을 가중치로서 사용함으로써 state 에서의 value function을 다른 모든 state들의 value function을 이용해 구할 수 있게 된다.
당연히, 다른 모든 state를 구하는 방법은 현재 알 수 없고(유기적으로 연결되어 있기 때문에 너무나도 복잡하다), 후에 배울 것입니다.
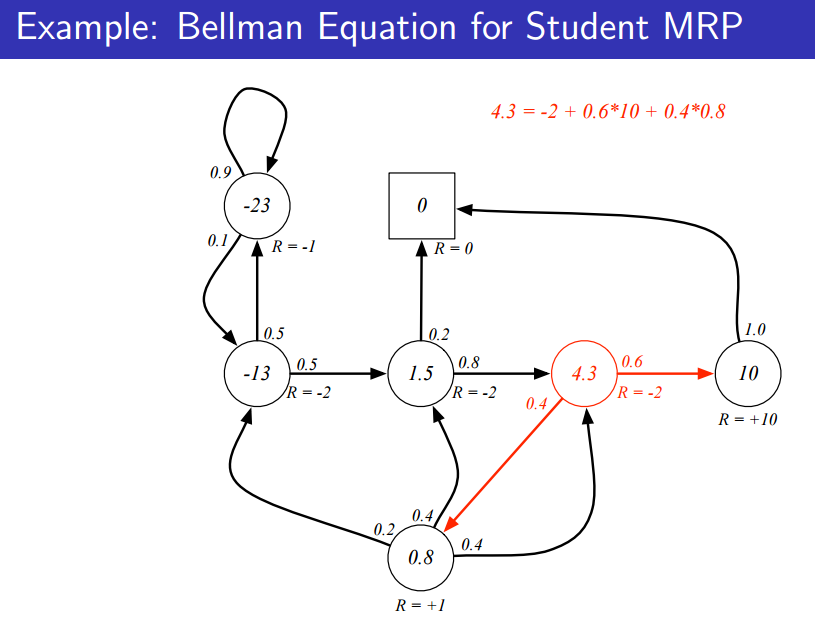
위처럼 4.3의 value function을 도출해내는 것을 보면 벨만 방정식이 성립하는 것을 알 수 있다.
식이 성립하는 것을 확인하는 것 뿐이지, 위의 값을 정확히 구한 것이 아니다.

이와 같은 상황을 위처럼 행렬로 깔끔하게 표현할 수 있게 된다.

식을 위처럼 전개해보자.
그러면, 이 주어진다면 value function을 한 번에 풀 수 있게 된다.
하지만, MRP의 정의 상 위의 값 는 무조건 알 수 있기에 사실상 (연산만 해결된다면) value function의 direct solution을 무조건 알 수 있는 것.
연산량()이 많기 때문에 큰 MRP는 한 번에 구하기는 힘들다. 여러 프로그래밍을 거쳐야 구할 수 있게 된다.
3.Markov Decision Processes(MDPs)
MDP

Markov Decision Process(MDP)는 MRP에서 (Action들의 집합)이 더해진 과정이라 할 수 있다. 즉, state간 전이 상황에서 action이라는 요소까지 고려한 과정이다.
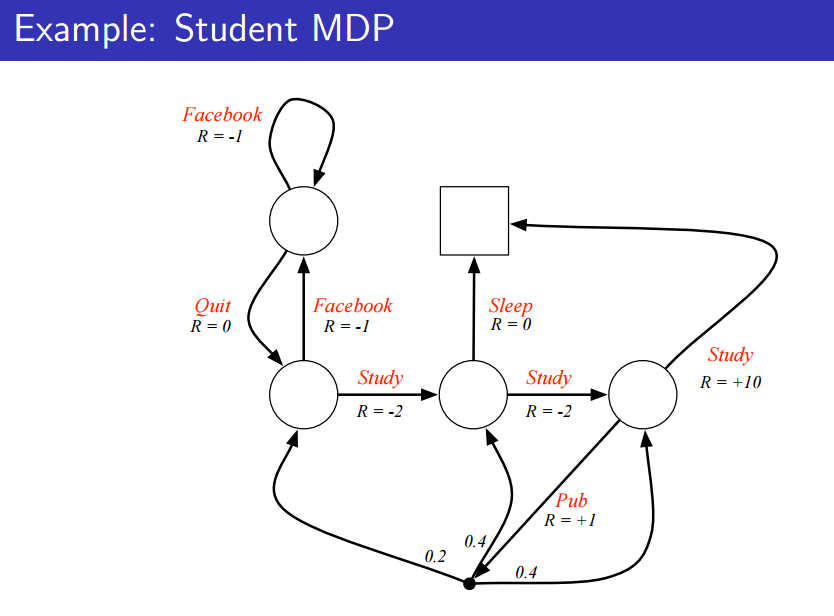
state에 reward가 주어지는 게 아닌, action에 reward가 주어진다.
이 때, action을 한다고 어떤 state로 무조건 가는 것은 아니고, 정해진 전이확률에 따라 확률적으로 움직이는 것이다.
이 때, MRP는 전이 매트릭스가 로 주어져 matrix였는데, MDP는 action이 주어지기 때문에 로 표현되기에 차원은 훨씬 큰 것을 알 수 있다.
Policies

MRP에선 action이 없기 때문에 policy가 필요 없었다. MDP는 action이 중요하기 때문에 특정 policy를 따라 action을 정해줄 필요가 있다.
MDP도 여전히 Markov process이기 때문에 현재의 state만 주어지면 policy는 유일하게 정해진다(history까지는 필요 없다).
즉, MDP는 environment, policy는 agent에 관한 내용이라 할 수 있습니다.

MDP에서는 policy 를 따라 에피소드가 정해진다.
이 때, state 가 주어지고, agent의 policy가 고정됐을 때의 전이 확률 매트릭스 가 주어진다면 MDP는 Markov Process라 할 수 있다.
즉, 위와 같은 상황이라면 현재의 상태 만 주어진다면 후에 agent가 겪게 될 environment들을 모두 계산(결정)할 수 있다는 것입니다.
또한 policy가 고정됐을 때의 Reward 를 추가로 알 수 있다면 그 때는 MRP로 바라볼 수 있게 된다.
이런 성질들로 무엇을 할 수 있을까? (...)
Value Function

여기서는 MDP의 state-value function을 살펴보자.
이 때, policy 가 정해지는 것 빼곤 MRP의 value function이랑 다를 것 없다.
다만, 거기에 action-value function 가 추가된다. 이는 policy와 state가 주어지고 action까지 정해졌을 때의 Return의 기댓값이라 할 수 있다.
이는 Q function이라고도 합니다.
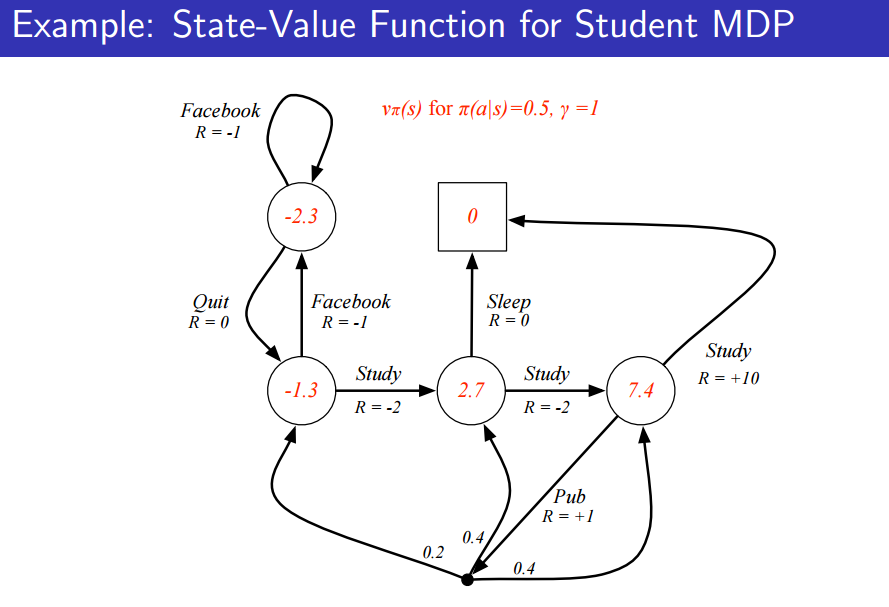
여기서의 policy는 모든 state의 action의 확률이 1/2으로 정의된다. discount factor는 1이라 가정한다.
Markov process에서는 벨만 방정식을 통해 행렬로 나타낸 다음 value function만 남기고 모두 이항하는 방식으로 value function을 구했다.
큰 문제에서 학습시킬 때 벨만 방정식이 기초가 되기 때문에 하는 것입니다.
Bellman Expectation Equation

여기서도 벨만 방정식을 이용해 관계들을 표현해보자.
표현 자체는 이전의 MRP와 거의 동일하다.
단, 식에서 , 이 나온다는 점이 차이점이다.

- 수식 표현(를 로 표현할 수 있다)
action-value function이 q인데, 그에 대한 가중치가 주어지는 것처럼 바라보면 된다. 이 때는, state 에서 action 를 했을 때의 state-value function을 나타내는 것이다.

- 수식 표현(를 로 표현할 수 있다)
마찬가지로, action 가 주어졌을 때 가능한 모든 state와 그에 따른 전이 확률을 가중치로 주어 linear sum을 해주면 된다. 여기서는, state 에서 action 를 했을 때 도착한 state에 대한 state-value function에 대한 값이므로 discount factor인 가 존재하는 것이다.

위의 , 에 대한 식을 이용해 위와 같이 에 대한 식만 남길 수 있다.
검은 점은 action이고, 흰 점은 state이다. 위의 그림을 보면 node가 더 생긴 것을 볼 수 있다.
유사하게,
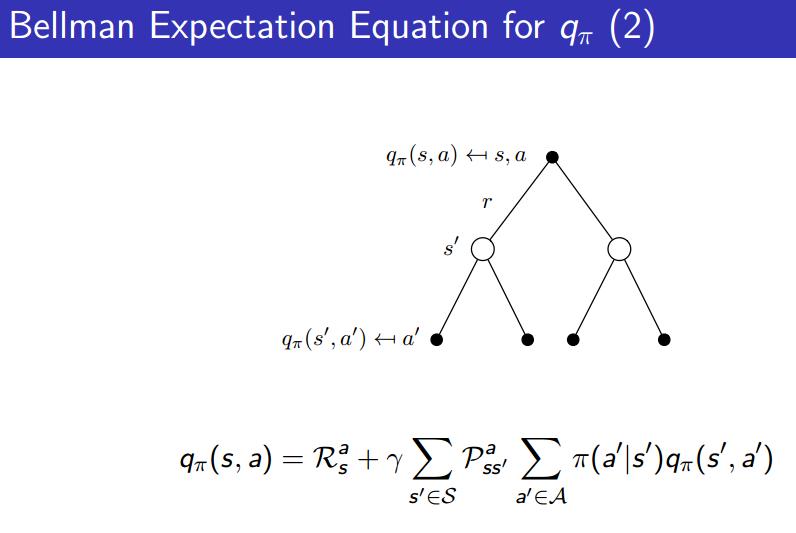
마찬가지로 위처럼 에 대한 식만 남길 수 있다.
그림이 굉장히 직관적으로 도움되므로 보는 것이 좋다.
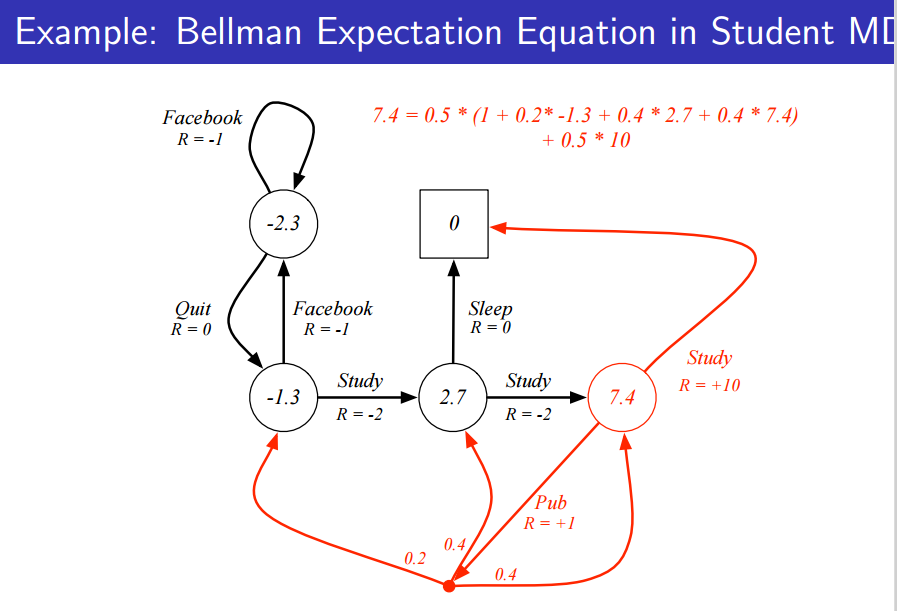
마찬가지로 모든 action의 확률이 0.5인 policy를 따를 때 위처럼 식이 완벽함을 볼 수 있게 된다.
위의 그림은 state value function입니다.

그 후, 최종적으로 MRP와 같이 Direct한 matrix form을 형성할 수 있게 된다.
지금까지는 policy를 대강 가정한 후 value function을 구하는 문제를 풀었습니다.
아래부터는, 이 policy를 어떻게 짜는 게 좋을 지에 대한 얘기입니다.
Optimal Value Function

위에서 말하는 는 가능한 모든 policy에 대한 최적값을 말한다. 즉, optimal state-value function 는 가장 좋은 state-value function 값을, optimial action-value function 는 가장 좋은 action-value function 값을 말한다.
즉, Optimal value function을 구했다면 MDP를 풀었다고 봐도 된다.
policy는 거의 무한하기 때문에 쉽지 않은 문제임을 알 수 있다.
큰 문제는, 행렬로 표현되지 않는다는 것.
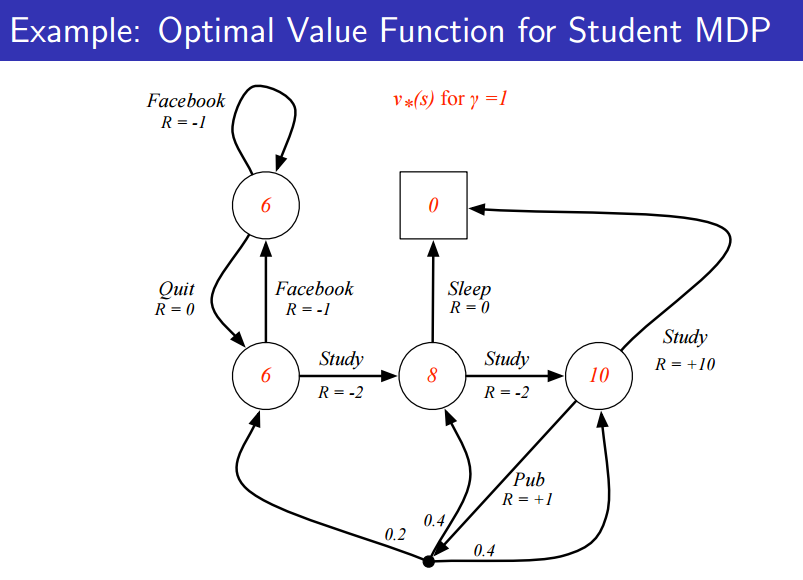
위 그림은 Student MDP인데, 빨간 숫자가 Optimal value function이다.
위의 그림은 역산하면 구할 수 있을 것이다.
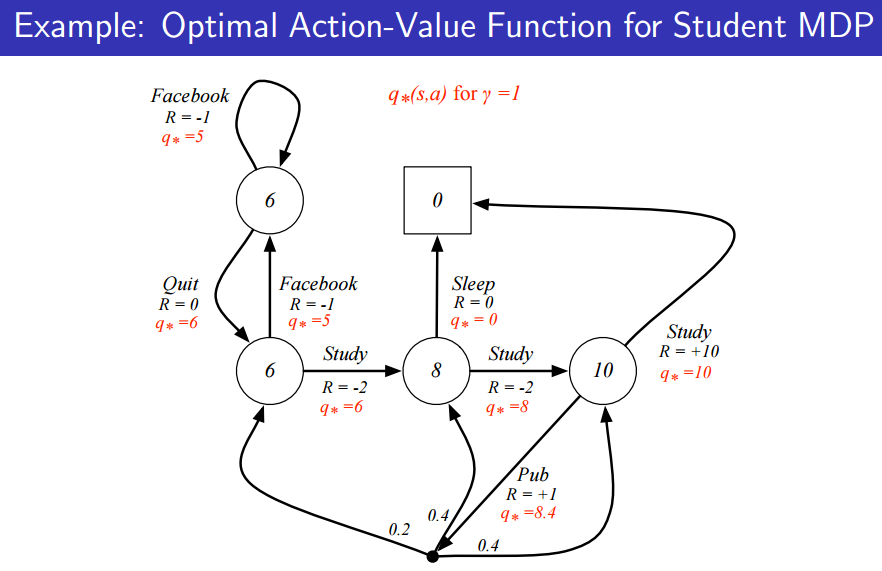
위 그림은 Optimal Action-value function이다. 이 때, 각각의 action에 대한 최적 값을 나타낸다.

Optimal Policy란 어떤 policy 2개가 주어졌을 때 항상 정할 수 있는 건 아니다. 하지만, 어떤 경우에서는 우위를 따질 수 있는데, 그를 partial ordering이라 한다.
조금 엄격한 조건이라 할 수 있다.
- 모든 MDP에 대해, optimal policy는 존재한다.
- 모든 optimal policy를 따라가면 optimal value function도 따라온다.
- 이는 optimal action-value function에도 적용된다.

직관적으로 당연한 정리일 수 있으나, 를 찾을 수 있다면 그를 만족하는 action a를 정함으로써 optimal policy를 위와 같이 찾을 수 있게 된다는 말이다.
즉, Optimal policy는 를 최대화 함으로써 얻을 수 있습니다.
모든 MDP 문제에서는 policy는 원래 stocastic한다. 하지만, 위처럼 정의하면 deterministic policy가 된다.
즉, 최적의 policy는 항상 존재하며, 그는 사실상 deterministic policy가 존재한다 할 수 있다. 심지어 가위바위보에도.
아무튼, 를 알면 된다.
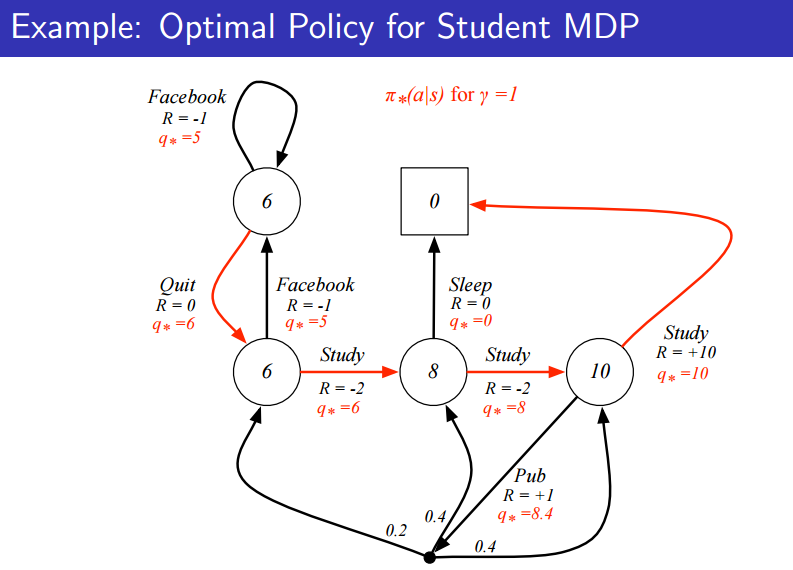
위에서 Optimal policy는 자명하게 deterministic하게 결정된다. 하지만, 위의 state가 몇 만개가 된다면? optimal policy를 찾기 쉬울까?
Bellman Optimality Equation

위와 다 똑같은데, action 을 따라 state 에서 를 최대화하는 경우 그 값은 가 된다.
벨만 방정식은 사실상 와 의 관계를 정립한 것이라 말할 수 있었습니다.
즉, state 에서 할 수 있는 action이 굉장히 많을 것이다. 이 때, a가 정해짐에 따라 를 최대화할 수 있게 되고 그 값은 와도 같아진다는 것이다.

를 로 표현할 수도 있다. 최적의 state value function 를 추종하면 된다.


그 사실들을 조합하면, 위의 그림들처럼 와 를 recursive하게 표현할 수 있게 된다.(위 그림들의 첫번 째에서 max에 괄호가 빠졌다)
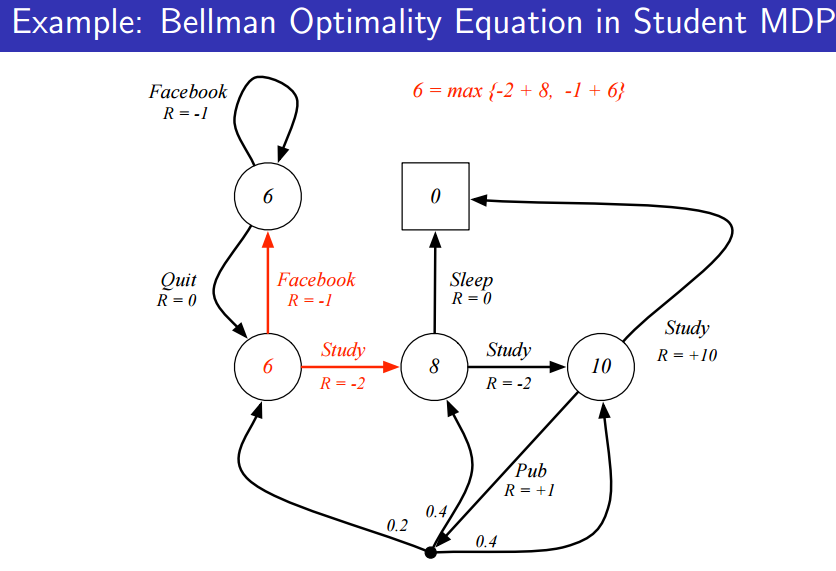
state value function에서의 벨만 최적화 방정식을 확인하면 위와 같다.
문제는, max라는 식은 선형식으로 표현할 수 없기 때문에, 정해진 form의 해를 구할 수 없다는 것입니다.

Optimality Equation은 비선형 문제이기 때문에 solution을 바로 구할 수 없어, 위와 같은 방법들을 통해 (근사적으로) 구해야 한다.
결론적으로, 복잡한 문제의 최적 해는 뒤에 나올 여러 방법들을 배워 학습을 통해 구하게 된다.