[개념정리] Attention Mechanism
What is Attention?
Attention이 처음 나오게 된 것은, many to many 중 '기계 번역' task를 더 잘 풀기 위함이였습니다. Attention을 Sparse하게 가져갈 것인지, Hard에게 가져갈 것인지에 따라 모델이 또 다르고, Attention을 이미지에 적용할 수도, 그래프에 적용할 수도 있습니다. 어텐션을 잘 활용하게 되면 Recurrent-based model을 사용하지 않아도 괜찮지 않겠냐는, Transformer 모델 또한 널리 쓰이고 있습니다. 또한, softmax를 주로 활용하기 때문에 softmax에 대해서도 깊게 살펴볼 필요가 있습니다.
Attention에 관련된 연구로, Attention이라는 단어가 쓰이지는 않았지만 어텐션 개념을 제공한 연구(바다나우 어텐션)와 Attention 개념을 깔끔하게 정립한 연구(루옹 어텐션)으로 나뉩니다. 해당 연구는 아래에서 소개합니다.
1. Bahdanau Attnetion - Paper : Neural Machine Translation by Jointly Learning to Align and Translate

사실, Attention 모델의 기반이 되는 논문임에도 불구하고 본문에 Attention이라는 단어가 나오진 않지만, 너무나도 중요한 논문입니다.
위의 제목에서, Jointly Learning To Align 에서 Align이 Attention의 역할을 하는 단어로 볼 수 있습니다.
기계번역은 당연하게도 NLP 쪽에선 제일 중요한 분야 중 하나라 할 수 있습니다. 이전까지는 고전 통계학을 이용해 기계번역을 수행했지만, neural machine translation을 이용해서도 통계기반 기계 번역에 버금가는 성능을 보였습니다. 해당 neural machine traslation은 Encoder-decoder 구조로 이루어져 있으며, fixed-length vector가 과거의 많은 정보를 담고 있습니다. 하지만, 그런 fixed-length vector는 과거의 정보를 담기엔 무리가 가는, bottleneck 이라 할 수 있고, 이를 조금 확장할 필요가 있었습니다. 그래서 저자들은 softmax를 활용한 automatically soft search를 도입했습니다. 성능이 굉장히 좋았다고 합니다.
2. Luong Attention - Effective Approaches to Attention-based Neural Machine Translation
Attention 단어를 본격적으로 사용한 모델입니다.
Attention Mechanism(어텐션 메커니즘)
이하 글은 딥러닝을 이용한 자연어처리 입문, 유원준 님의 자료를 토대로 작성하였습니다.
NLP의 기존 모델 seq2seq에서는 인코더가 입력 시퀀스를 context vector로 압축하고, 디코더는 이 벡터를 통해서 출력 시퀀스를 만들어 냅니다.
하지만, 이렇게 고정된 사이즈의 vector로 압축해 사용하는 모델은 아래와 같은 문제점이 존재합니다.
- fixed-size의 vector의 모든 정보를 저장하기 때문에 정보 손실이 일어난다.
- RNN의 고질적인 문제인 Vanishing Gradient(기울기 소실), 즉 Long-term problem이 존재한다.
이는 자연어처리 task에서 입력 시퀀스(문장)이 길어질수록 성능이 떨어지는 현상으로 나타납니다. 이를 해결하기 위해 제안된 기법이 어텐션(Attention) 기법입니다.
1.어텐션(Attention)의 아이디어
어텐션의 기본 아이디어는 디코더에서 출력 단어를 예측하는 매 시점(step)마다, 인코더의 입력 시퀀스를 다시 참고하는 것입니다. 이 때, 입력 시퀀스를 동일한 비중으로 참고하는 것이 아닌, 예측 단어와 관련이 있는 입력 단어를 더욱 치중해서 보기 때문에 Attention이란 단어를 사용합니다.
2. 어텐션 함수(Attention Function)
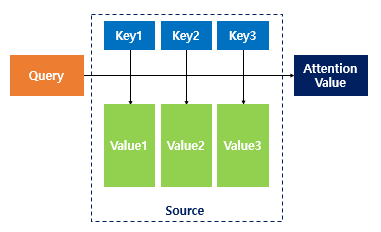
어텐션 함수를 기호를 사용해 표현하면 아래와 같이 표현할 수 있습니다.
어텐션 함수는 주어진 '쿼리(Query)'에 대해 모든 '키(Key)'의 유사도를 각각 구합니다. 그리고, 이 유사도를 키(Key)와 매핑되어 있는 각각의 '값(Value)'에 반영해줍니다. 그리고, '유사도가 반영된' 값(Value)을 모두 더해서 리턴하고, 어텐션 값(Attention value)를 반환합니다.
3. 닷-프로덕트 어텐션(Dot-Product Attention)
아래에서 다룰 Attention은 트랜스포머에 쓰이는 Attention과 다른, seq2seq에 Attention 기법을 적용한 예시(바다나우 어텐션)의 기본 형태인 Dot-product Attention)입니다. 수식이 간단할 뿐, 근본적으로 다른 어텐션 기법과 큰 차이는 없어 설명에 용이합니다.
어텐션 구조의 가장 기본이 되는 Dot-Product Attention에서는 위의 쿼리, 키, Value(Q, K, V)가 아래와 같습니다.
- : Query - 시점의 decoder cell에서의 은닉 상태
- : Key - 모든 시점의 encoder cell에서의 은닉 상태
- : Value - 모든 시점의 encoder cell에서의 은닉 상태
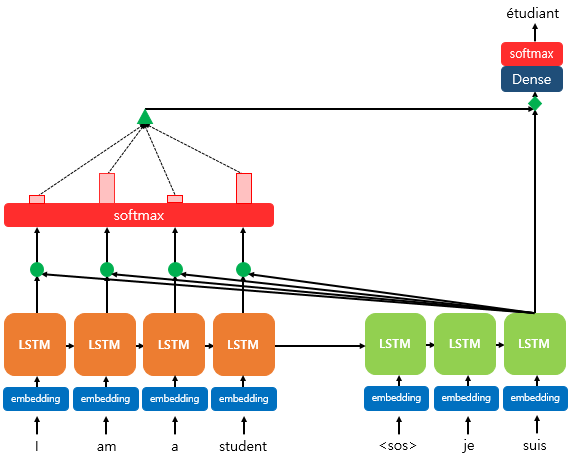
위 그림은 Decoder의 세번째 LSTM Cell에서 출력 단어를 예측할 때 어텐션 메커니즘을 사용하는 예시입니다.
Attention 메커니즘을 적용함으로써, 세번째 단어를 예측할 때 예측 단어와 encoder의 모든 시퀀스('I', 'am', 'a', 'stduent')의 관계를 파악하게 됩니다.
이 때, 파악하는 방식은 그림 내에도 존재하는 soft max를 이용함으로써 이루어집니다.
그림의 왼쪽 부분처럼, 세번째 cell에서 출력 단어를 예측할 때 softmax를 통과시킨 input sequence(즉, 확률분포; 위 그림의 초록색 삼각형)를 추가적으로 전달함으로써 decoder가 새로운 단어를 예측하는 데 있어서 Recurrent하게 전달된 정보 외에도 input sequence의 정보를 참고할 수 있는 길(path)을 마련하게 됩니다.
자세한 연산 과정을 살펴봅시다.
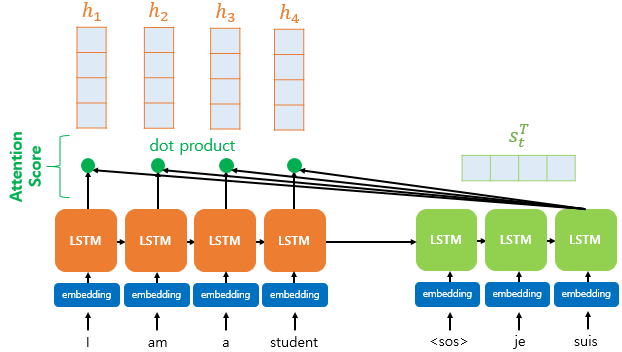
위의 그림에서 나오는 기호에 대해 간단히 적고 넘어가겠습니다.
: t 시점에서 encoder의 hidden state (예시에서 4차원)
: t 시점에서 decoder의 hidden state (예시에서 4차원)
만약 Attention기법을 사용하지 않는다면 decoder는 time step (예시) 에서 새로운 단어를 예측하기 위해 이전 step의 hidden state인 와 이전 step의 output 총 2개를 필요로 합니다.
이와 별개로, Attention을 사용할 경우 위에서 말한 , 외에도 Attention value 를 추가로 필요로 합니다.
아래에서 Attention value 을 구하기 위한 가정을 디테일하게 살펴봅시다.
Attention value 을 구하기 위해서는 크게 아래의 세 과정을 거쳐 얻을 수 있습니다.
- , 를 활용해 Attention Score()를 구한다.
- softmax를 활용해 Attention Distribution을 구한다.
- 인코더에서, 2.에서 구한 분포를 토대로 결정한 가중치와 hidden state를 가중합하여 Attention Value를 구한다.
차례대로 살펴봅시다.
3.1. , 를 활용해 Attention Score()를 구한다.
Attention Score(어텐션 스코어)는 디코더의 time step 에서 새로운 단어를 예측하기 위해, decoder의 hidden state 와 encoder의 hidden states ~들이 얼마나 유사한지를 판단하는 점수입니다.
아래 그림은 decoder의 time step 에서 hidden state 와 encoder의 time step 에서 hidden state 의 어텐션 스코어를 구하는 과정을 나타냅니다.
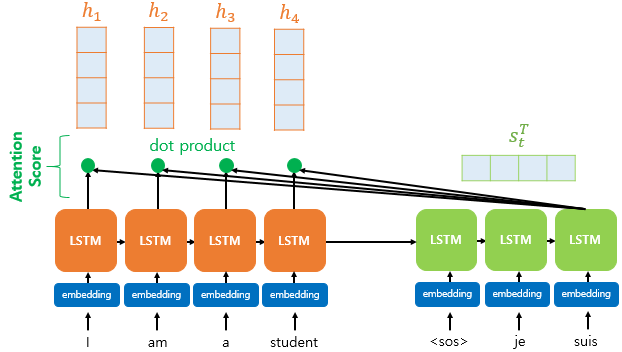
위의 그림에 따르면, 와 의 Attention Score는 아래와 같은 식으로 결정됩니다.
이 때 결과 값은 scalar가 됩니다.
decoder의 time step은 인 반면, 참고하는 encoder의 time step은 부터 까지 있기 때문에, encoder의 모든 은닉 상태에 대한 decoder의 time step 에서의 Attention score를 계산하면 아래와 같이 나타낼 수 있습니다.
=[s_t^{T}h_1, ..., s_T^{T}h_N]
3.2. softmax를 활용해 Attention Distribution을 구한다.
위에서 얻은 Attention scores 에 softmax(소프트맥스)함수를 적용해, 모든 값의 합이 이 되는 확률 분포 Attention Distribution을 얻습니다.
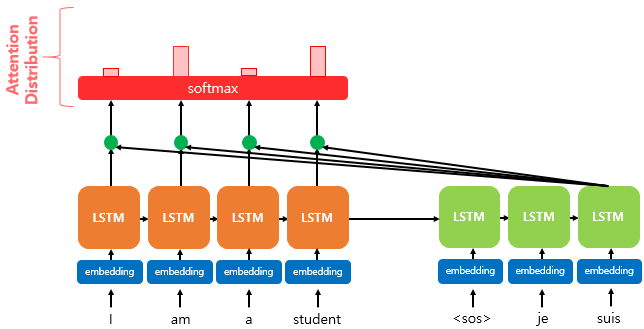
즉, 위의 그림에 있는 Attention Distribution을 얻기 위해 아래와 같은 식을 사용하면 됩니다.
가 아닌 입니다.
예를 들어, 입력 시퀀스인 ['I', 'am', 'a', 'student']에 대응하는 hidden states를 활용해 Attention scores를 구하고, 이로부터 Attention Distribution을 구하게 되면 의 형태를 갖는 벡터를 얻게 됩니다.
이 때 각각의 값을 Attention Weight(어텐션 가중치)라고 합니다.
3.3. 인코더의 각 Attention Weight와 그에 대응하는 hidden state를 가중합하여 Attention Values를 구한다.
최종적으로, 위에서 구한 Attention Weight와 각 hidden state를 통해 최종적인 Attention value 를 얻습니다.
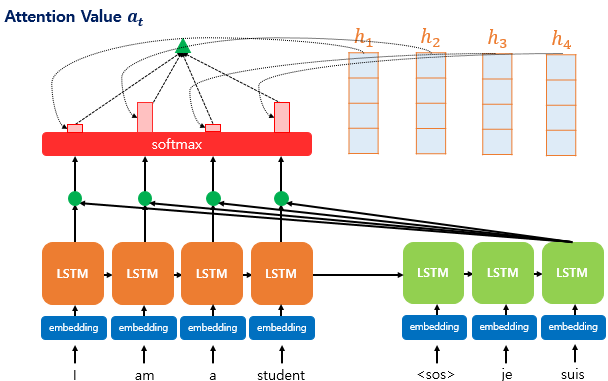
이에 대한 식은 아래와 같이 기술할 수 있습니다.
이러한 어텐션 값 는 인코더의 맥락을 포함하고 있기 때문에 Context Vector(맥락 벡터) 라고도 불립니다(정확히는, decoder 내 time step 의 context vector)
즉, 기존의 seq2seq 기반 모델들이 Encoder의 마지막 hidden state를 fixed-size context vector로 사용하는 것과 대조적입니다.
그렇다고 기존의 fixed-size context vector를 사용하지 않는 건 아닙니다만..
위에서 구한 어텐션 값 를 활용해 최종적인 예측까지의 과정을 살펴봅시다.
3.4. Attention value 와 decoder의 시점의 hidden state를 연결(concatenate)합니다.
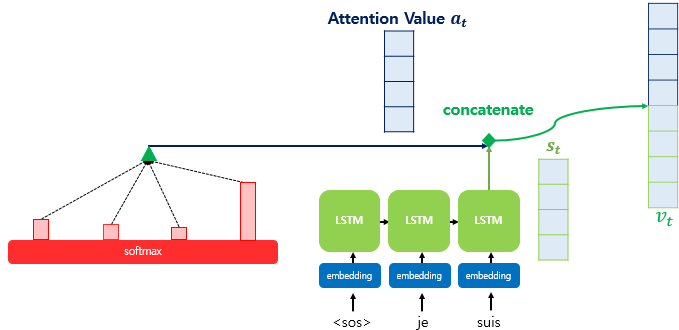
위에서 구한 Attention value 를 단순하게 decoder의 시점의 hidden state 와 연결(concatenate)해줍니다. 연결한 벡터를 라고 가정하면, 는 기존의 Recurrent하게 얻은 decoder의 hidden state의 정보 외에도 encoder에서의 모든 hidden state를 고려한 정보 또한 포함하고 있기 때문에, sequence가 길어지더라도 정보를 크게 잃지 않습니다.
그리하여, decoder는 새로운 예측 값 를 더욱 더 좋은 성능으로 반환할 수 있게 됩니다.
encoder의 hidden state와 decoder의 hidden state를 같다고 가정했고, Attention value 는 encoder의 hidden state로부터 나오기 때문에 는 우선 decoder의 hidden state와도 차원이 같습니다. 꼭 같아야 하는 것은 아닙니다.
단, 해당 연구에서는 에서 를 바로 반환하는 것이 아닌, 추가적인 신경망 연산을 통해 차원을 다시 와 맞춰준 다음 를 반환하게 됩니다.
3.5. 출력층 연산의 input이 되는 를 계산합니다.
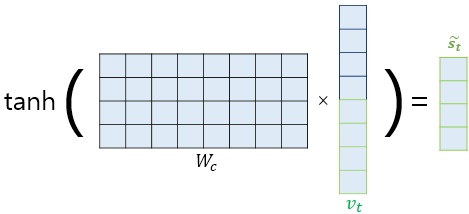
위 연산에 대한 식은 아래와 같이 간단하게 나타낼 수 있습니다.
위에서 는 학습 가능한 가중치 행렬이고, 는 편향입니다. 위에서 말한 가 의 형태로 들어갑니다. 는 concat을 나타냅니다.
3.6. 최종적인 예측 를 얻습니다.
4. Various Attention
위에서 소개한 Dot-product Attention 외에도 다양한 어텐션 종류가 있습니다.
큰 틀은 거의 동일하지만 중간 수식(Attention score)이 다르기 때문에 다른 Attention으로 불립니다.
예를 들어, dot-product Attention은 Attention score를 구할 때 내적을 사용하기 때문에 dot-product Attention으로 불립니다.
다양한 Attention 방법의 예시는 아래와 같습니다.

그림 참고 : https://wikidocs.net/22893
5. 결론.
위에서는 seq2seq의 단점(Long-term problem)을 해결하기 위해 Attention 기법을 '추가적으로' 사용한 예시를 나타냈습니다.
다만, 글의 초반부에 말했다시피 요즘은 Attention 자체가 거의 seq2seq를 대체하는 방법으로 사용되고 있습니다.
이에 대해서는 자연어처리, 컴퓨터 비전 분야에서 상당한 영향력을 끼치고 있는 Transformer 에서 더욱 자세히 다루겠습니다.
자세한 설명 감사합니다.