[이론&코드] Transformer in Pytorch
본 글은 아래의 자료를 메인으로 참고하였습니다.
이론 : 딥러닝을 이용한 자연어처리 입문, 유원준
코드 : https://github.com/hyunwoongko/transformer
Attention is all you need - Base paper
트랜스포머의 기반이 되는 논문으로, 3만회에 달하는 피인용을 기록하고 있는 연구입니다. 트랜스포머는 자연어처리 분야에서 SOTA 성능을 보였고, 최근 이미지 분야에까지 널리 사용되고 있는, 최근 딥러닝에서 빼놓을 수 없는 모델입니다.
Paper: Attention is all you need
Transformer(트랜스포머)
기존의 seq2seq 모델은 인코더에서 마지막의 hidden state, 즉 fixed-size context vector에 모든 정보가 압축됩니다. 이를 이용해 디코더가 예측을 하게 된다면, 입력 시퀀스의 길이가 길어지면서 정보 손실의 가능성이 생깁니다.
이를 해결하기 위해 Attention(어텐션)이 쓰였습니다. 이를 이용해, seq2seq를 아예 대체하는 encoder-decoder 모델을 구현할 수 있고, 이를 Transformer(트랜스포머) 구조라 합니다.
1. Hyperparameter of Transformer
- 트랜스포머의 인코더와 디코더에서 정해진 입력과 출력의 크기입니다. 임베딩 벡터(embedding vector)의 차원과 동일하며, 인코더와 디코더 내에서 값이 전달될 때의 차원 또한 동일합니다.
- encoder와 decoder를 총 몇 층으로 쌓을지에 대한 하이퍼 파라미터입니다.
- 트랜스포머에서는 어텐션을 사용할 때 하나로 진행하는 것보다 여러 개기 병렬로 어텐션을 수행하고, 결과 값을 하나로 합치는 방식을 택합니다. 이 때 해당 병렬의 개수를 말합니다.
- 트랜스포머 내부에는 Feed-forward 신경망이 존재합니다. 이 때의 은닉층의 크기를 의미합니다. 즉, d_{ff 차원에서 차원으로 임베딩이 진행됩니다.
2. Transformer
트랜스포머에서는 Encoder와 Decoder가 개만큼 존재할 수 있습니다.
seq2seq 구조에서는 각각 하나의 RNN이 개의 시점을 가지는 반면, 기본적으로 트랜스포머에서는 개의 Encoder, Decoder가 존재합니다(변경 가능합니다).
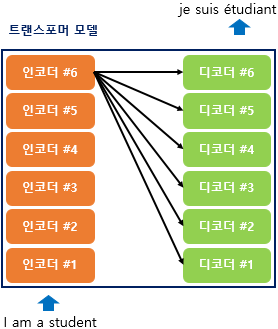
즉, 각각 6개가 존재하는 Encoder, Decoder를 Encoders, Decoders로 깔끔하게 나타낼 수 있습니다.
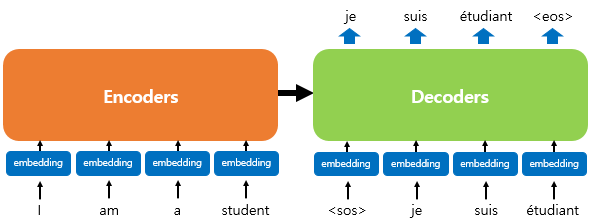
이처럼, 기존의 RNN 기반 모델과 비슷한 구조를 가지기에 디코더에서 start token <sos>를 가지고, end token <eos>를 가지는 것 또한 비슷합니다.
다만, 기존 방법론들은 각 단어의 임베딩 벡터를 곧바로 input으로 받는 반면, 트랜스포머에서는 인코더와 디코더에서 임베딩 벡터에서 조정된 값을 input으로 받습니다.
이를 Positional Encoding(포지셔널 인코딩)이라 합니다.
3. Positional Encoding
먼저, 트랜스포머에서의 입력을 구체적으로 알아보기 위해 포지셔널 인코딩의 개념부터 살펴봅시다.
RNN은 단어의 위치에 따라 단어를 순차적으로 입력받아 처리하는 특성을 가집니다. 즉, 각 단어의 위치 정보(position information)을 가집니다.
하지만, 트랜스포머에서는 단어를 순차적으로 입력받지 않기 때문에 단어의 위치 정보를 다른 방식으로 알려주어야 합니다. 트랜스포머는 해당 단어의 위치 정보를 얻기 위해 각 단어의 임베딩 벡터에 위치 정보들을 더하여 모델의 최종적인 입력으로 사용합니다.
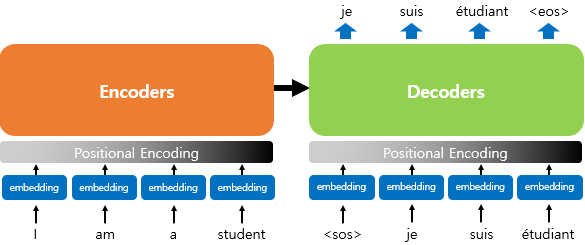
즉, 위의 그림처럼 단어들의 임베딩 벡터가 트랜스포머의 입력으로 들어가기 전에 포지셔널 인코딩 값이 더해집니다.
포지셔널 인코딩 값이 더해지는 과정을 시각화하면 아래와 같습니다.

위의 그림의 색만 봐도 대강 어떤 식으로 더해질 것인지는 알겠지만, 구체적으로는 어떤 식을 통해 위치 정보가 주어질까요?
포지셔널 인코딩에는 다양한 종류가 있지만, 우선 기본적으로 sin 함수와 cos 함수를 이용해 위치 정보를 전달합니다.
위 식에는 등의 인자가 들어 있습니다. 이를 포함한 위의 식을 이해하기 위해서는, 위에서 본 임베딩 벡터와 포지셔널 인코딩의 덧셈은 실제로 임베딩 벡터가 모여 만들어진 문장 벡터 행렬과 포지셔널 인코딩의 덧셈 연산을 통해 이루어진다는 것을 먼저 이해할 필요가 있습니다.
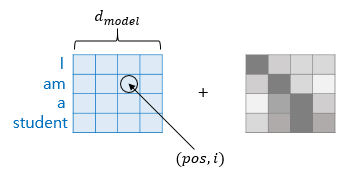
- : 입력 문장에서 임베딩 벡터의 위치(e.g., I는 'I am a student'의 1번째)
- : 임베딩 벡터 내 차원의 인덱스 (즉, 을 따라 인덱싱)
- : 트랜스포머의 모든 층의 출력 차원을 나타내는 하이퍼 파라미터(기본 512)
위의 시작에 따르면 , 즉 임베딩 벡터 내 각 차원의 인덱스가 짝수일 때는 sin함수를, 홀수일 때는 cos함수를 사용합니다.
위와 같은 포지셔널 인코딩 방법을 사용할 경우 순서 정보가 보존됩니다.
예를 들어, 같은 임베딩 벡터(단어)임에도 불구하고 포지셔널 인코딩 값을 더하게 된다면 최종적으로 트랜스포머의 입력 값은 달라집니다.
Pytorch code of Positional Encoding
import torch
import matplotlib.pyplot as plt
import numpy as np
from torch import nn
class PositionalEncoding(nn.Module):
def __init__(self, d_model, max_len, device):
"""
sin, cos encoding 구현
parameter
- d_model : model의 차원
- max_len : 최대 seaquence 길이
- device : cuda or cpu
"""
super(PositionalEncoding, self).__init__() # nn.Module 초기화
# input matrix(자연어 처리에선 임베딩 벡터)와 같은 size의 tensor 생성
# 즉, (max_len, d_model) size
self.encoding = torch.zeros(max_len, d_model, device=device)
self.encoding.requires_grad = False # 인코딩의 그래디언트는 필요 없다.
# 위치 indexing용 벡터
# pos는 max_len의 index를 의미한다.
pos = torch.arange(0, max_len, device =device)
# 1D : (max_len, ) size -> 2D : (max_len, 1) size -> word의 위치를 반영하기 위해
pos = pos.float().unsqueeze(dim=1) # int64 -> float32 (없어도 되긴 함)
# i는 d_model의 index를 의미한다. _2i : (d_model, ) size
# 즉, embedding size가 512일 때, i = [0,512]
_2i = torch.arange(0, d_model, step=2, device=device).float()
# (max_len, 1) / (d_model/2 ) -> (max_len, d_model/2)
self.encoding[:, ::2] = torch.sin(pos / (10000 ** (_2i / d_model)))
self.encoding[:, 1::2] = torch.cos(pos / (10000 ** (_2i / d_model)))
def forward(self, x):
# self.encoding
# [max_len = 512, d_model = 512]
# batch_size = 128, seq_len = 30
batch_size, seq_len = x.size()
# [seq_len = 30, d_model = 512]
# [128, 30, 512]의 size를 가지는 token embedding에 더해질 것이다.
#
return self.encoding[:seq_len, :]
시각화
50 × 128의 크기를 가지는 포지셔널 인코딩 행렬을 시각화하여 어떤 형태를 가지는지 확인해봅시다. 이는 입력 문장의 단어가 50개이면서, 각 단어가 128차원의 임베딩 벡터를 가질 때 사용할 수 있는 행렬입니다.
sample_pos_encoding = PositionalEncoding(128, 50, device='cpu')
plt.pcolormesh(sample_pos_encoding.encoding.numpy(), cmap='RdBu')
plt.xlabel('Depth')
plt.ylabel('Position')
plt.colorbar()
plt.show()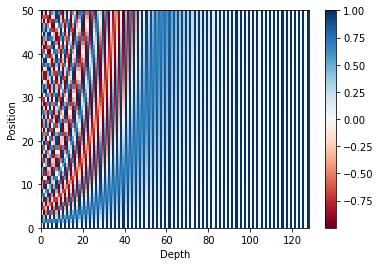
4. 어텐션(Attention)
트랜스포머에는 세 가지의 어텐션이 사용됩니다.
Self-Attention of Encoder, Masked Self-Attention of Decoder, Co-Attention Between Encoder and Decoder.
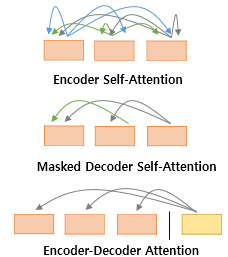
Self-Attention은 Query, Key, Value가 동일한 경우를 말하며, Co-Attention에서는 Query가 Decoder의 vector, Key, Value가 Encoder의 Vector가 됩니다.
이 때, Query, Key, Value가 동일하다는 것은 서로 값이 같다는 것이 아닌, 출처 자체가 Encoder에서만 나오거나, Decoder에서만 나오거나 한다는 것입니다.
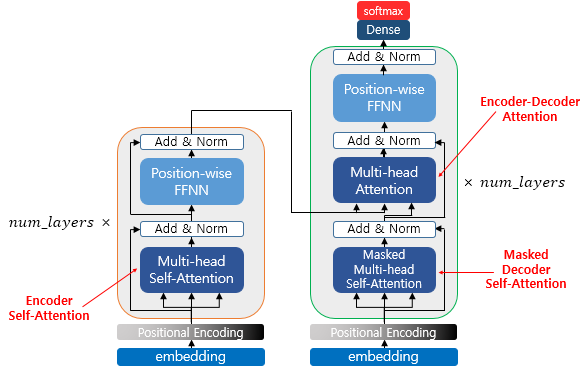
위의 그림은 각 종류의 Attention이 수행되는 위치입니다.
이 때, 각 어텐션은 Multi-head로 이루어져 있는데, 이는 Attention을 병렬적으로 수행하는 추가적인 차원을 말합니다.
5. 인코더(Encoder)
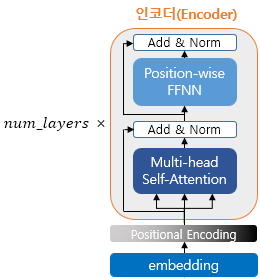
인코더는 하이퍼 파라미터 에 따라 해당하는 개수만큼 인코더 층을 쌓습니다.
하나의 층을 기준으로 봤을 때에는 Self-Attention 층과 Feed Forward Network 층으로 나뉩니다.
5.1. 인코더의 Self-Attention
Self-Attention의 의미 & 이점
Attention 함수는 주어진 '쿼리(Query)'에 대해 '모든 키(Key)'와의 유사도를 각각 구해줍니다. 이 유사도를 가중치로 활용하여 Key와 매핑되어있는 Value와 가중합하게 됩니다.
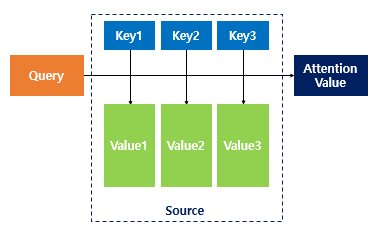
그러면, Self-Attention은 어떤 역할을 할까요?
기존의 어텐션은 아래와 같습니다.
Q = Query : 시점의 디코더 셀에서의 은닉 상태
K = Keys : 모든 시점의 인코더 셀의 은닉 상태들
V = Values : 모든 시점의 인코더 셀의 은닉 상태들
이 때, 어차피 모든 시점 에 대해 적용될 것이기 때문에 아래와 같이 전체시점에 대해 확장할 수 있습니다.
Q = Querys : 모든 시점의 디코더 셀에서의 은닉 상태들
K = Keys : 모든 시점의 인코더 셀의 은닉 상태들
V = Values : 모든 시점의 인코더 셀의 은닉 상태들
이처럼, 일반적으로 Query 는 디코더 셀의 은닉상태 였고, 는 인코더 셀의 은닉상태 였기에, 는 서로 다른 값을 가집니다.
하지만, 셀프 어텐션에서는 가 모두 동일합니다.
Q : 입력 문장의 모든 단어 벡터들(입력 시퀀스)
K : 입력 문장의 모든 단어 벡터들
V : 입력 문장의 모든 단어 벡터들
그러면, 이처럼 입력 시퀀스에 대해 스스로 어텐션 과정을 거치는 것이 어떤 의미가 있을까요?

The animal didn't cross the street because it was too tired.
위에서 it은 animal일까요 street일까요?
셀프 어텐션은 위처럼 하나의 입력 문장 내에서 특정 단어들끼리의 유사도를 구함으로써 위와 같이 it이 무슨 문장인지 또한 파악할 수 있습니다.
Get vectors of Q,K,V
셀프 어텐션은 인코더의 초기 입력인 차원의 시퀀스를 곧바로 사용하는 것이 아닌, 그보다 더 작은 차원을 갖는 벡터를 얻습니다.
위에서 의 차원(default 64)은 다른 하이퍼 파라미터인 **에 의해 결정됩니다.
즉, 초기 입력 시퀀스의 차원 과, 어텐션의 을 사용한다면 각 벡터의 차원은 가 됩니다.
우선 student라는 단어 벡터 하나에 대해서 벡터 변환하는 모습을 봅시다.
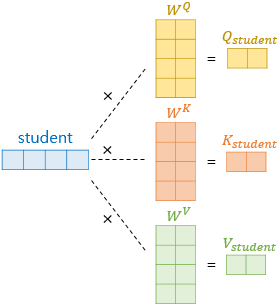
기존의 차원에서 차원으로 줄이기 위해서 일반적인 가중치행렬()를 곱해주면 됩니다.
위와 같은 과정을 거쳐 각각의 단어(I, am, a, student)는 보다 낮은 차원의 로 변환됩니다.
Scaled dot-product Attention
그 이후에는, 기존의 어텐션과 마찬가지로 특정 Q벡터가 모든 K 벡터에 대해 연산하여 Attention Score -> Attention Distribution를 구하고, 이를 토대로 모든 V 벡터와 가중합되어 Attention Value(Context vector)를 구하게 됩니다.
위의 과정을 모든 Q 벡터에 대해서 수행합니다.
트랜스포머에서는, Attention Score를 구하는 과정에서 일반적인 dot product가 아니라, scaled dot product를 사용합니다.
즉,
가 아닌
을 사용합니다.
이 때 는 각 Q,K,V 벡터의 차원인 입니다.
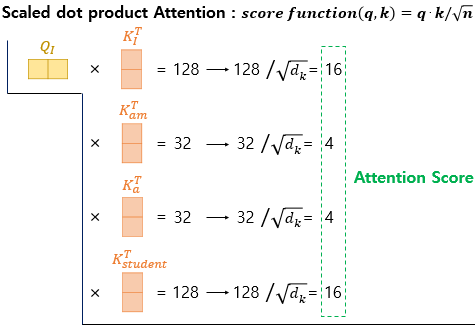
위처럼 각 Attention score를 구하고, soft-max를 통과시켜 Attention Distribution을 구한 다음, V벡터와 가중합해 Attention Value를 구합니다.
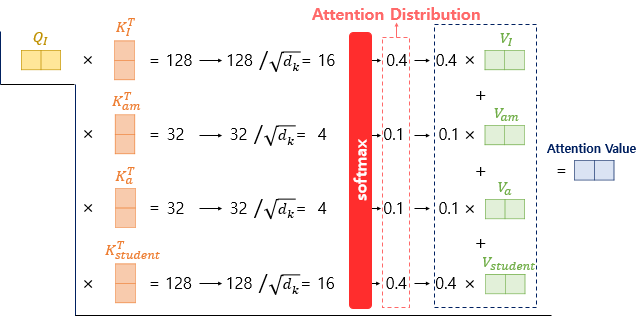
위의 상황에서, 특정 Query(Q 벡터)는 단어 'I'를 가지기에 위의 Attention value를 단어 'I'에 대한 context vector라고도 부릅니다.
하지만, 위처럼 특정 Q vector에 대한 어텐션 값을 일일히 구할 필요가 있을까요?
당연히, 그냥 행렬 연산을 수행해주면 됩니다.
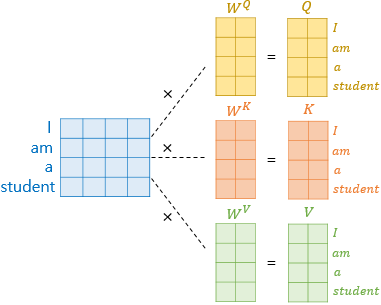
그러면, 위와 같이 모든 시퀀스에 대한 Q,K,V 벡터를 얻을 수 있습니다.
Attention Score & Attention 역시 단순하게 행렬곱으로 처리할 수 있습니다.
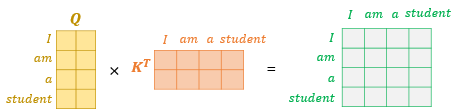
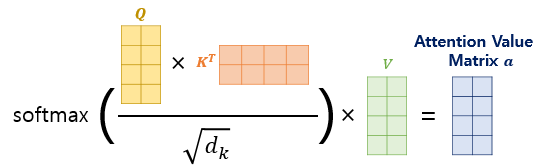
즉, 위의 결과를 통해 실질적으로 트랜스포머 논문에 나와있는 수식이 도출됩니다.
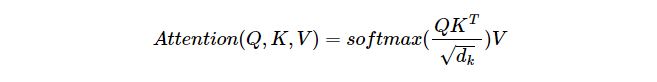
Dimension
입력 시퀀스는 각각의 단어가 차원을 갖습니다.
즉, 입력 문장의 차원은 입니다.
여기에, 3개의 가중치 행렬을 곱해 행렬을 만들어야 합니다.
이 때, 행렬의 차원을 각각 라 합시다.
와 는 직접적으로 행렬 연산이 행해져야 하기 때문에 차원이 같아야 하며, 그 이후에 곱해지는 는 차원이 같을 필요가 없습니다.
그러면, **WQ, W_K, W_V$는 $d{model}$ 차원에서 차원으로 줄이기 위해 각각 차원을 갖습니다.
그러면, 최종적인 차원은 아래와 같습니다.
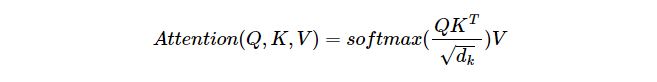
물론, 논문에서는 그냥 를 모두 의 값으로 사용합니다.