As-Rigid-As Possible Surface Modeling

ARAP은 메쉬 변형 알고리즘이다. CGAL에도 구현되어있고, python으로도 Open3D 통해서 사용할 수 있다. Vertex 수천개 정도 스케일에서는 꽤 빠르게 돌아가는 편이다.

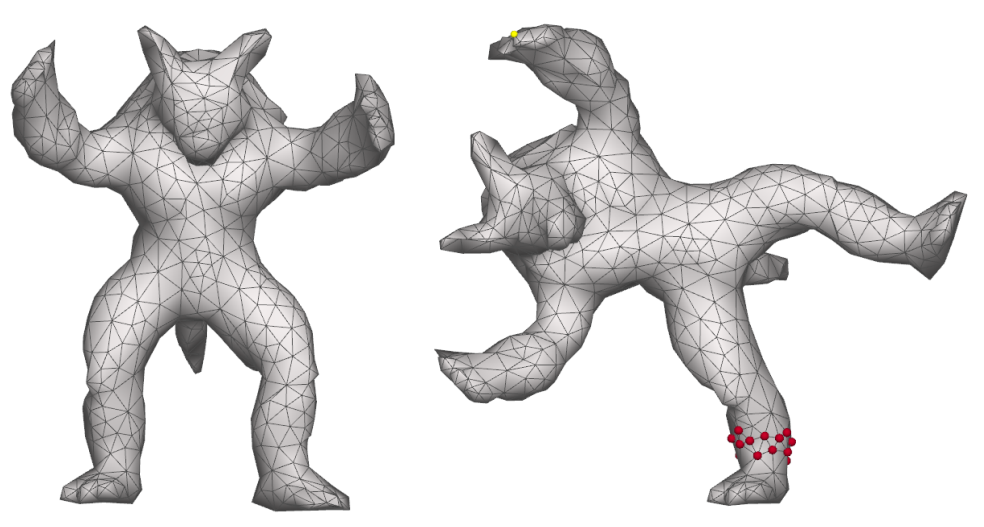
ARAP으로 변형한 Armadillo. 오른쪽 그림에서 오른쪽 다리의 빨간 점들이 fixed point이고 왼손의 노란 점이 handle이다.

배경

두 surface 사이의 차이는 shell energy라는 것을 통해 측정할 수 있는데

$\mathbf{I}$와 $\mathbf{II}$는 각각 first, second fundamental form이다. $\mathbf{I}$은 surface의 strechting과 관련 있고, $\mathbf{II}$는 bending과 관련 있다. 따라서 만약 surface $\mathcal{S}$과 $\mathcal{S}'$사이의 deform이 rigid하면 shell energy는 0이다. Non-rigid 한 deform을 찾을 때에도, shell energy가 0은 아니더라도 최소화 되도록 찾으면 (as-rigid-as possible 하게), local한 shape이 유지될 수 있다.

Cell $\mathcal{C}_i$ (여기선 vertex $i$의 one-ring neighborhood로 정의)와 deform된 버전 $\mathcal{C}_i'$에 대해 deformation이 rigid하다면 rotation matrix $\mathbf{R}_i$로

로 나타낼 수 있다. $\mathbf{p}_i$는 vertex 좌표. $\mathcal{N}(i)$는 vertex $i$의 neighborhood (참고로,
$\forall j\in \mathcal{N}(i)$에 대해 $i\in\mathcal{N}(j)$이므로 cell들은 overlapping되어 있다.). Deformation이 non-rigid면 deform을 제일 잘 approximation하는 $\mathbf{R}_i$는 아래의 weighted square를 minimize하는 것이다.

$\mathbf{p}_i-\mathbf{p}_j$를 $\mathbf{e}_{ij}$로 적자. 그럼 위 식은 다시 쓰면

나머지 항은 상수니까 $\mathbf{R}_i$을 포함하는 term만 minimize할 수 있는데,

Weighted inner product를 trace를 사용한 형태로 변형시키면 ($Tr(\mathbf{y}\mathbf{x}^T)=\mathbf{x}^T\mathbf{y}$),

이다.

$\mathbf{S}_i$를 $\mathbf{e}_{ij}$로 구성된 $3\times|\mathcal{N}(i)|$ 행렬 $\mathbf{P}_i$와 $w_{ij}$로 구성된 $|\mathcal{N}(i)|\times|\mathcal{N}(i)|$ 대각행렬 $\mathbf{D}_i$를 이용해서 쓸 수 있다. 만약 행렬 $\mathbf{M}$이 PSD이면 어느 orthogonal 행렬 $\mathbf{R}$에 대해서도 $Tr(\mathbf{M})\geq Tr(\mathbf{RM})$이므로, $\mathbf{R}_i \mathbf{S}_i$를 symmetric PSD로 만드는 행렬 $\mathbf{R}_i$가 $Tr(\mathbf{R}_i\mathbf{S}_i)$를 maximize한다. 그러한 $\mathbf{R}_i$ 는 SVD해서 ($\mathbf{S}_i = \mathbf{U}_i \mathbf{\Sigma}_i\mathbf{V}^T_i$)

를 통해서 구할 수 있다.

구체적인 메소드

앞에서 정의했던 cell에 대한 에너지를 전체 surface에 대해 합하면

이 때, weight $w_i$와 $w_{ij}$를 어떻게 골라야 할까? Deformation energy가 최대한 mesh-independent 하기 위해서 (특히 이 경우 non-uniform한 cell의 영향을 줄이기 위해서) cotangent weight을 사용한다.

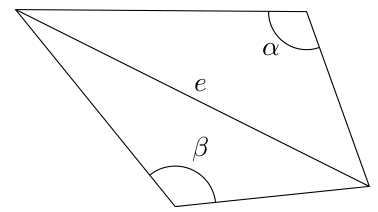
$\alpha$와 $\beta$는 $\mathbf{e}$에 마주보고 있는 angle이다. Computing Discrete Minimal Surfaces and Their Conjugates을 참조하면 Dirichlet energy란 함수가 얼마만큼 변화하는가에 대한 measure이다($E_{D}(f)=\frac{1}{2}\int_{\Omega}|\nabla f|^2$). 이런 surface에서 angle-preserving 한 mapping을 구하려면, 얼마만큼 Cauchy-Riemann equation을 만족하느냐를 나타내는 conformal energy라는 것을 사용하면 되는데, 이 conformal energy를 minimize하는 것이 Dirichlet energy 빼기 mapping area를 minimize하는 것과 동치라고 한다(https://math.stackexchange.com/questions/3213598/what-are-the-use-cases-of-the-dirichlet-energy-in-computer-vision 참조). 아무튼 계산해보면 triangle간의 linear map에 대한 Dirichlet energy가

가 된다 한다. 이 내용을 ARAP에서 이용한 것이다. Cell energy가 cell area에 비례하는데 Voronoi area를 이용해서 normalize 해줄 수 있다.

우리가 ARAP을 통해 하고 싶은 것은 sparse한 user input을 constraint으로 두고, 나머지에 해당하는 vertex의 위치를 적절히 결정하고 싶은 것이다. 따라서 우리는 문제를 $\mathbf{p}’$에 대해 풀어야한다. 또 $\mathbf{R}$ 역시 찾아야한다. 그래서 두 step으로 나눠서 한번은 $\mathbf{R}$을 고정하고 $\mathbf p’$를 찾고, 한번은 $\mathbf p’$를 고정하고 $\mathbf R$을 찾는다.

먼저 각 i에 대해 $\mathbf{R}_i$을 찾는 것은 서로 독립적이므로 앞서 언급한 $\mathbf{S}_i$의 SVD를 이용한 방식으로 찾을 수 있다. (참고로, ARAP 외에 다른 deform 방식 중에는 이웃한 $\mathbf{R}_i$ 이 서로 비슷한 값을 갖도록 유도하는 것들도 있다.)

$\mathbf{p}'_i$는 partial derivate를 이용해서 찾을 수 있다.

이 때, $w_{ij}=w_{ji}$ 이므로

derivative가 0이 되려면

왼쪽 term은 discrete Laplace-Beltrami operator가 $\mathbf p'$에 적용된 형태임을 볼 수 있다. 따라서 $\mathbf{Lp}'=\mathbf{b}$ 꼴이고 Cholesky decomposition을 이용해서 빠르게 풀 수 있다. (https://en.wikipedia.org/wiki/Cholesky_decomposition 의 application 항목 첫번째 문단 참조)

앞서 이웃한 $\mathbf{R}_i$ 이 서로 비슷한 값을 갖도록 유도하는 것들도 있다고 했는데, 이 term을 ARAP에 더한 것이 Smoothed Rotation Enhanced As-Rigid-As Possible (SR_ARAP) Deformation 이고 cell energy term에 $\|\mathbf{R}_i-\mathbf{R}j\|^2_{F}$을 더한다.