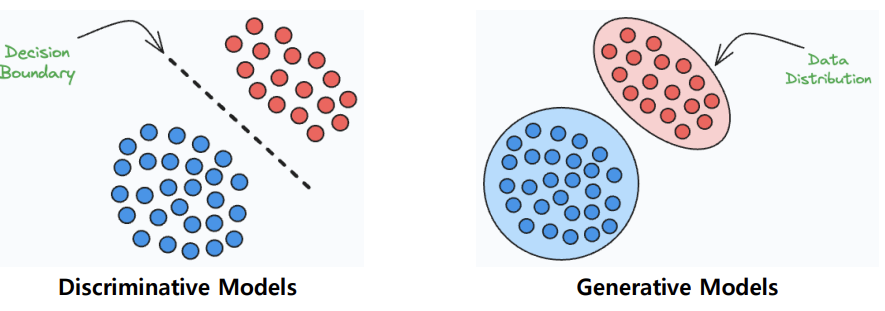
Discriminative Model(구분 모델)
: 서로 다른 클래스들을 구분하는 결정 경계(Decision Boundary)를 학습하는 모델
- 목표: Conditional probability (조건부 확률)을 최대화하는 것
-> 주어진 입력 x에 대해 정답 레이블 y의 확률을 최대화하는 것
Generative Model(생성 모델)
: 데이터 자체의 분포를 학습하는 모델
- 목표: 결합 확률 분포(joint propability distribution)를 최대화
-> 관찰 가능한 변수 x와 목표 변수 y의 결합 확률(joint prob. distribution)을 최대화
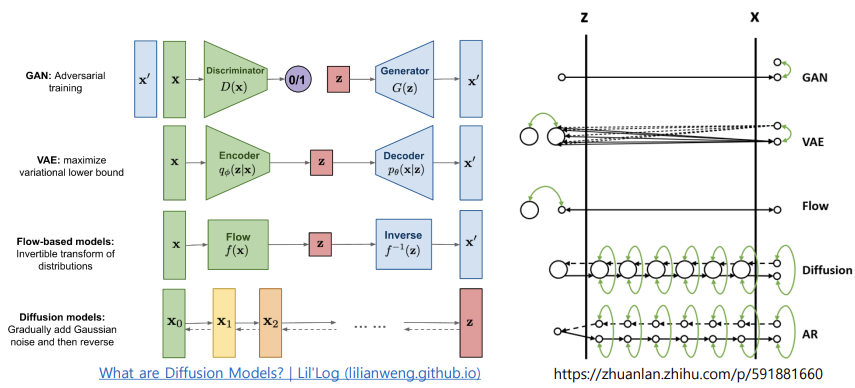
- Generative Models
: VAE, GAN, Normalizing Flow, Diffusion Models, Flow Matching
- VAE: maximize variational lower bound
-> 인코더(Encoder): 데이터를 잠재 공간의 확률 분포로 압축
디코더(Decoder): 잠재 공간에서 샘플링한 데이터를 원래 공간으로 복원
잠재 분포로 가우시안 분포를 가정하여 학습 - GAN: Adversarial training
- Flow-based models: Invertible trasform of distributions
- Diffusion models: Gradually add Gaussian noise and then reverse
- Autoencoder
목표: 데이터를 기반으로 효율적인 data representation을 학습
- Unsupervised learning (구체적으로는 Self-supervised learning)에 해당
-> 오토인코더는 데이터를 자체적으로 추정하면서(estimating) 학습됨
-> 학습 과정에서 label 정보 사용X
-> 대규모 unlabeled data 활용 시 유리
- Encoder
: 입력 데이터 기반으로 잠재 표현(Latent Representation)을 인코딩
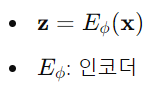
-> 잠재 표현 z의 차원은 입력 데이터 x의 차원보다 작아져 information bottleneck(정보 병목) 역할을 함
- Decoder
: 잠재 표현(Latent Representation)으로부터 데이터를 디코딩
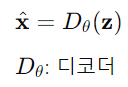
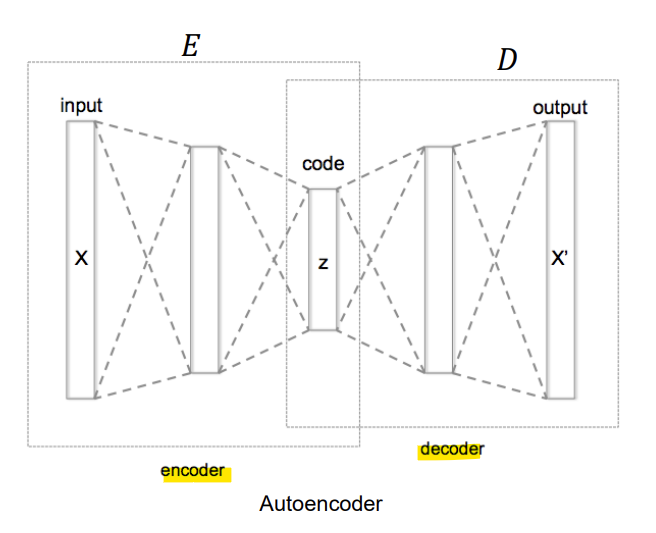
- Training

-> 원본 데이터 x와 예측된(생성된) 데이터 x' 사이의 거리를 최소화하는 것이 목표!
- Latent Representation
- Autoencoder는 데이터에 대한 효율적인 latent representation을 학습함
-> 일반적으로, 의미 있는 정보를 위해 차원을 축소함
-> 차원 축소 측면에서 주성분 분석(Principal Component Analysis, PCA)과 유사한 결과 도출
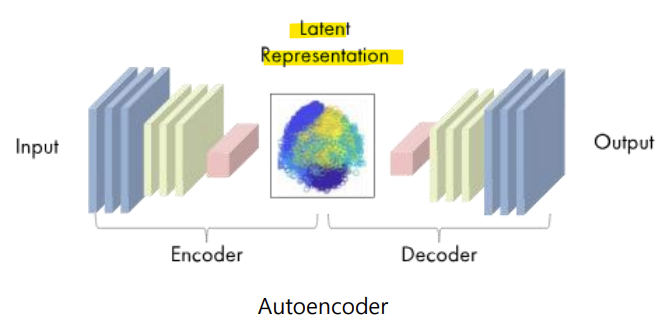
- Encoder
- pre-trained encoder는 특징 추출기(feature extractor)로 활용 가능
- encoder를 동결(freezing)하거나, 추가적인 분류기(classifier)와 함께 미세 조정(Fine-tuning) 가능
- 전이 학습(Transfer Learning): 특정 작업이나 데이터셋을 통해 얻은 지식을 다른 작업 또는 다른 데이터셋에서 모델 성능을 향상시키는 데 활용
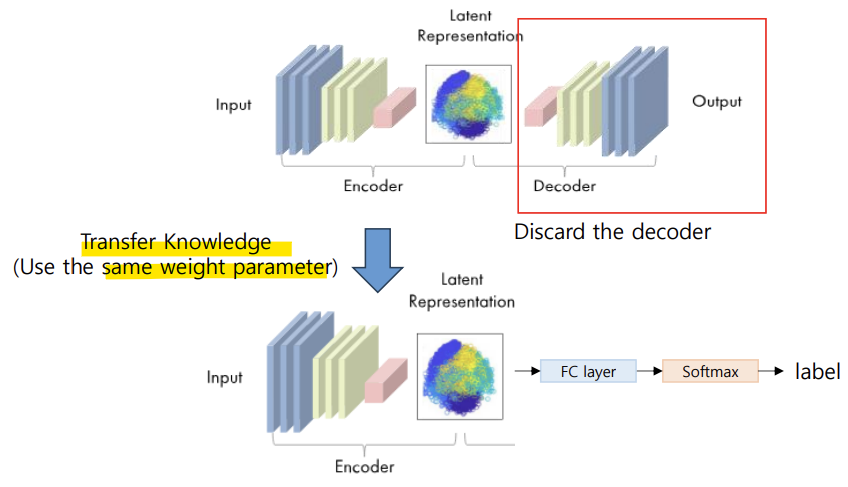
- Denoising Autoencoder
- 노이즈를 추가해 유용한 latent representation 학습
-> 랜덤 노이즈를 데이터에 추가한 후, 입력 데이터에서 잠재 표현(Latent Representation)을 인코딩 후, latent representation(z)로부터 데이터를 디코딩
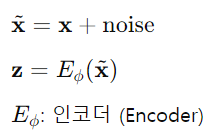

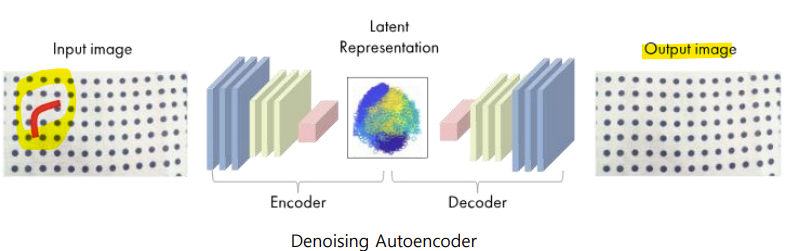
- Denoising Autoencoder: 기본(vanilla) 오토인코더에 약간의 수정이 가해진 형태
-> 현실 세계의 노이즈가 있는 데이터셋에서 노이즈를 줄이는 데 사용됨
-> 모델이 Latent representation에서 의미 있는 정보를 더 견고하게(robustly) 학습할 수 있도록 도움
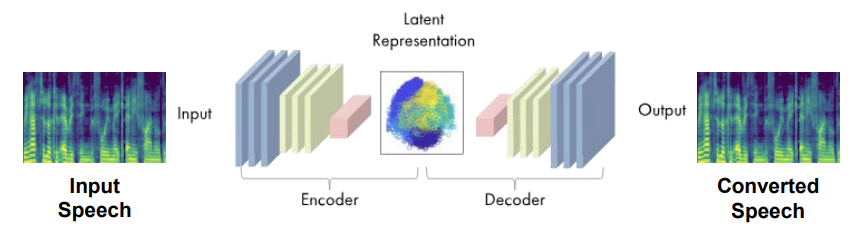
- Voice Conversion(음성 변환, VC)
: source speech의 내용 정보를 유지하면서, target voice의 스타일로 변환하는 기술
- AutoVC: 오코인코더 손실만으로 이루어진 Zero-shot voice style transfer
- Zero-shot Voice Style Transfer
: 학습되지 않은 화자의 음성을 변환 - Unseen speaker: 학습 과정에서 사용되지 않은 speaker
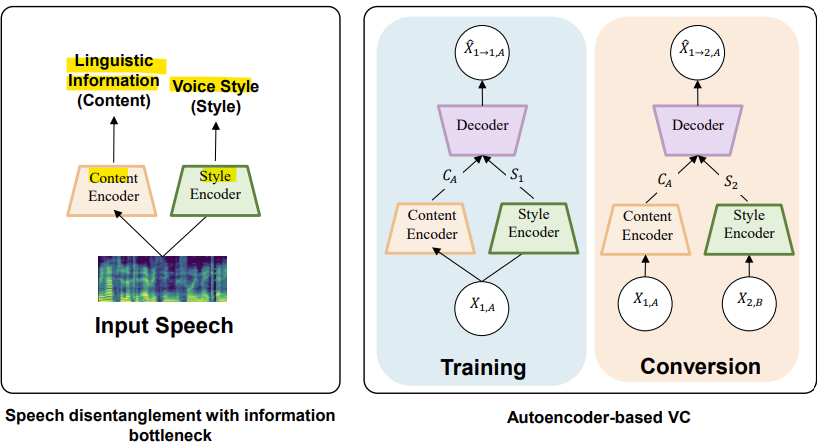
- Information Bottleneck for Voice Conversion
- Content Encoder
: 언어적 정보(linguistic information)를 시간적 컨텐츠 표현(Temporal Content Representation)으로 인코딩 - Style Encoder
: 음성 스타일 정보를 전역 스타일 표현(Global Style Representation)으로 인코딩
- Information Bottleneck(정보 병목)
: 랜덤 변수 X를 요약할 때, 정확도(Accuracy)와 복잡도(Compression)의 최적 절충점(Tradeoff)을 찾기 위해 설계됨
: 이는 X와 관찰된 관련 변수(observed relevant variable) Y 사이의 결합 확률 분포(joint probability distribution) p(X,Y)를 기반으로 함
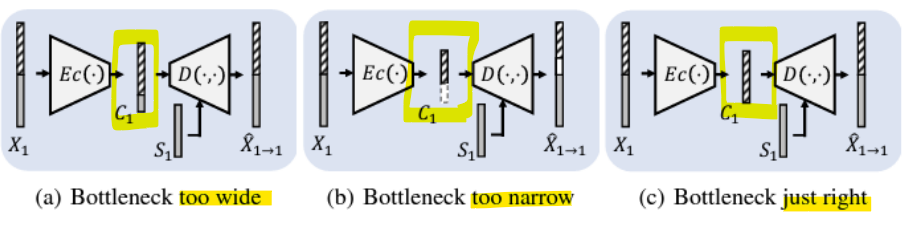
<적절한 information bottleneck 크기>
- 넓을 경우: voice info까지 인코딩될 수 있음
- 좁을 경우: content info가 손실될 수 있음
-> voice conversion을 위해서는 내용 정보만을 인코딩할 수 있는 적절한 병목 크기를 찾아야 함
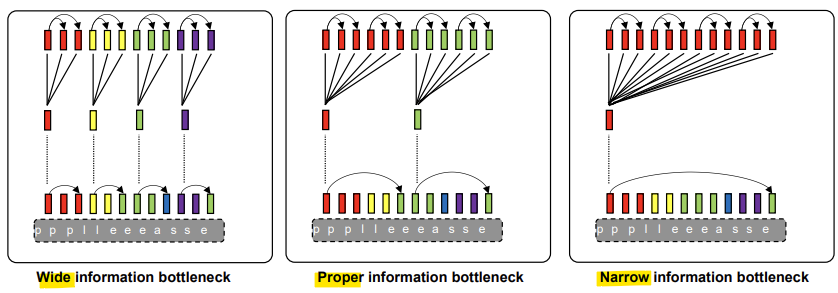
- Model Architecture
- Speaker Encoder
-
Mel-Spectrogram에서 마지막 layer의 표현을 평균화해서 글로벌 스타일 표현(global style representation)을 추출
-
Pre-training the speaker encoder
: GE2E 손실(Generalized End-to-End loss)을 사용 -
GE2E loss: Metric learning을 위한 손실 함수
-> 서로 다른 화자의 문장에서 나온 representation 간의 거리를 최대화
-> 동일한 화자의 문장에서 나온 representation 간의 거리를 최소화
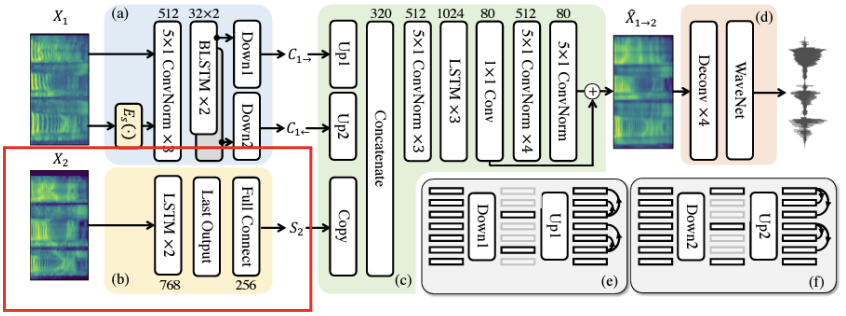
- Content Encoder
- 컨볼루션 네트워크 stack
-> 인접한 프레임(adjacent frames) 간의 언어적 정보(linguistic info)를 추출 - 양방향(Bi-directional) LSTM
-> speech sequences의 시간적 정보(Temporal Info)를 인코딩
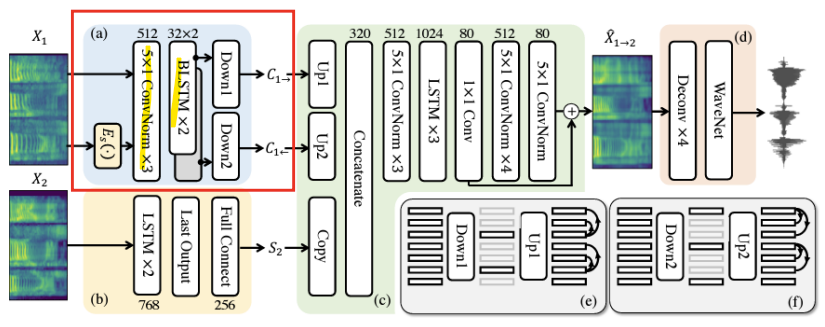
- 컨텐츠 정보를 위한 Information Bottleneck
- 적절한 정보 병목 크기는 컨텐츠 representation에서 voice style info를 제거할 수 O
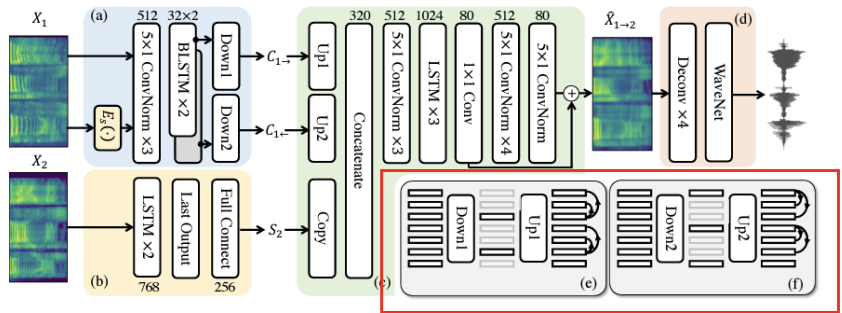
- Decoder
- content info와 speaker info를 결합(concatenation)
- concatenated features로부터 Mel-Spectrogram을 생성
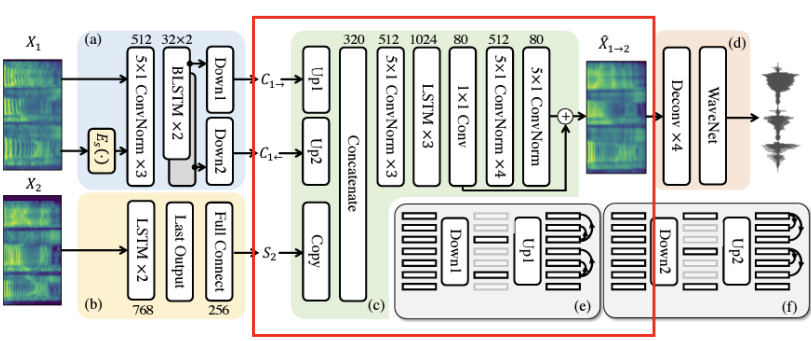
- Post-Net
- Residual Mel-Spectrogram을 보완(refinement)하여 재구성 품질(Reconstruction)을 향상시킴
- Training
- 초기 Reconstruction loss

- 전체 손실 L

-> 손실 함수를 최소화하여
1) 입력 데이터의 재구성 품질을 향상
2) 원본 입력 데이터와 컨텐츠 정보의 보존
3) 스타일 정보와의 분리 및 손실 간의 균형 조절할 수 있게 학습
- Evaluation
<Subjective Evaluation, 주관적 평가>
- 평균 의견 점수(Mean Opinion Score, MOS)
: 청취자가 변환 음성의 자연스러움을 평가
- 유사성(Similarity)
: 청취자가 변환된 음성과 목표 음성(Ground-Truth Target Speech)의 유사성을 평가
<Objective Evaluation, 객관적 평가>
- reconstruction error가 낮은 모델은 Mel-spectrogram을 더 잘 재구성할 수 O, 오디오 품질이 더 좋아질 수 O
- 그러나 speaker info가 높은 모델(content representation에서 화자 분류 정확도가 높은)은 voice style 변환을 제대로 수행하지 X
-> 따라서 음성 변환과 오디오 품질을 위해 적절한 information bottleneck 크기를 찾아야 함
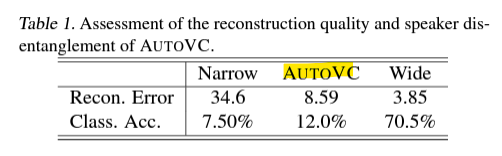
- Masked Autoencoder (MAE)
- 목표: self-supervised manner를 통해 풍부한 latent representation 학습
- 더 나은 효율성을 위해 Vision Transformer(ViT)의 patch를 masking
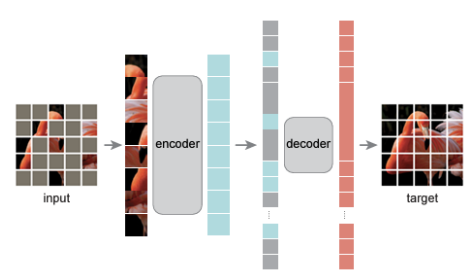
- MAE의 Down-stream 작업(모델 평가 및 응용하는 과정)
: COCO object detection 및 분할(segmentation) 등
- Audio-MAE
: Mel-spectrogram을 패치화하고, 오디오에 대한 풍부한 latent representation을 학습
- Down-stream tasks
: Sound Activity Detection(SAD), Speaker Identification Task(SID)

- Fre-painter
- 더 나은 latent representation을 위해 Audio-MAE를 Pre-training
- audio super-resolution을 위해 파형 생성기(waveform generator)를 추가하여 모델 Fine-tuning
1) Audio-MAE를 사용한 Pre-training
2) waveform generator를 추가한 Fine-tuning
-> waveform generator: 오디오 데이터를 최종적으로 고품질 원본 신호(waveform)로 변환하는 모듈
-> Mel-Spectrogram은 오디오의 주파수 정보를 포함하지만, 이를 다시 파형(waveform)으로 변환하려면 복원 작업이 필요
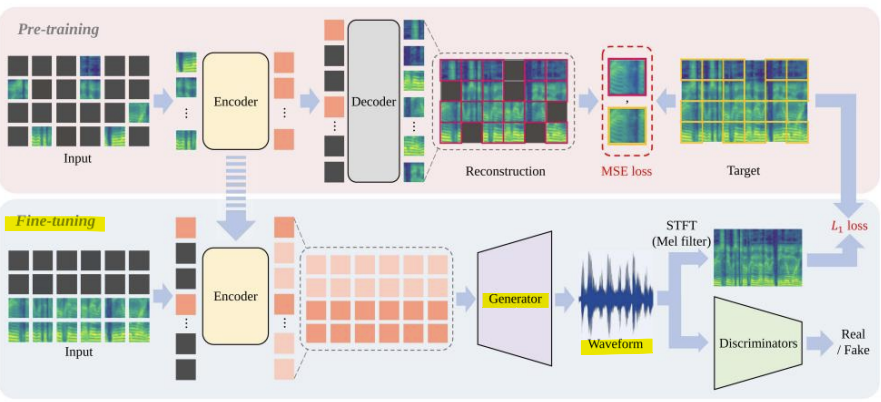
- 요약
- 오토인코더(Autoencoder)는 데이터의 효율적인 잠재 표현(latent representation)을 학습할 수 O
- 적절한 정보 병목(information bottleneck)이나 노이징(noising) 데이터를 활용한 오토인코더는 데이터의 구성 요소를 분리(disentangle)할 수 O
ex) 음성 분해(Speech decomposition) - 자기 지도 학습(Self-supervised representation learning) 모델은 유용한 특징 추출기(feature extractor)로 활용될 수 O
- Variational Autoencoder (VAE)
- 확률적 변분 추론(Stochastic variational inference)
연속적인 잠재 변수와 계산이 불가능한 사후 분포(intractable posterior distributions)가 존재하는 상황에서, 유도 확률 모델(directed probabilistic models)에서 효율적인 추론과 학습을 수행하려면 어떻게 할까?
- 변분(Variational): 어떤 함수를 최적화하기 위해 함수 공간을 탐색하는 기법(복잡한 확률 분포를 다룰 때 이를 근사하는 데 사용됨)
1) Latent space를 가우시안으로 정규화
-> 이는 사후 분포(posterior)가 대략적으로 가우시안이라고 가정하며, 알려진 데이터 포인트에서 샘플링하여 새로운 샘플을 생성할 수 있게함
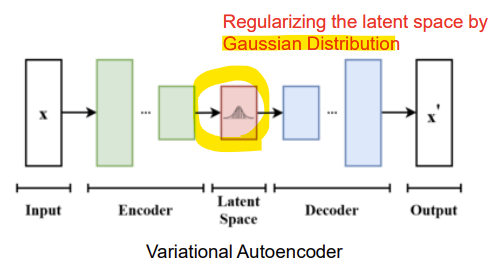
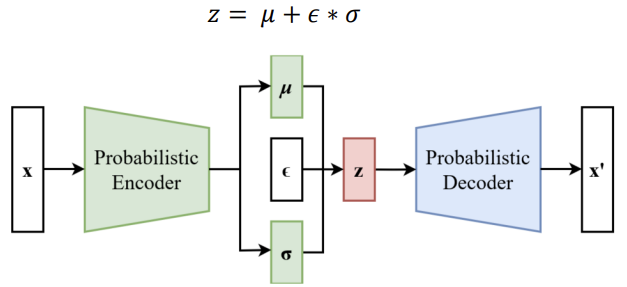
2) 변분 하한(Variational Lower Bound)을 위한 재매개변수화 기법(Reparameterization Trick)
-> Standard Stochastic Gradient Methods을 사용하여 하한 추정값(Lower Bound Estimator)을 최적화할 수 있게함
- The Evidence Lower Bound (ELBO)
: 복잡한 확률 모델에서 데이터 가능도(likelihood)를 효율적으로 최적화하기 위해 사용되는 접근 방식

데이터를 설명하는 모델을 학습하기 위해 데이터 가능도(likelihood)를 최대화하기 위해
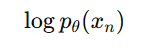
를 계산해야 함
p(x)는 주변 분포(Marginal Distribution)로 표현됨
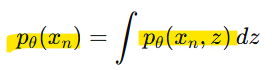

-> p(x)를 계산하려면 z를 적분해야 함(적분 과정에서 잠재 변수의 모든 가능한 값에 대해 확률을 합산해야 함)
<문제점>
-> z가 고차원일 경우: 계산 비용이 매우 큼(현실적으로 불가능할 수도 있음)
-> p(x,z)의 형태가 복잡할 경우: z에 대해 적분 수행 시 닫힌 형태의 해(analytical solution)가 존재하지 않을 수도 있음
<해결책>
-> 직접 계산이 어려운 p(x)를 간접적으로 계산하는 방법
-> 샘플링을 통한 근사 추정을 활용
-> q(z)라는 샘플링이 쉬운 임의의 분포를 도입하여 p(x)를 근사하기(ex. 가우시안 분포)
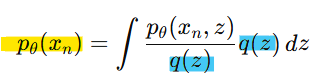
위 식은 다시 기대값(Expected Value)형태로 변환할 수 있음
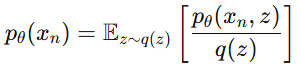
즉, q(z)로부터 샘플링된 값들을 활용해 p(x)를 근사적으로 추정할 수 있음
< q(z)가 유용한 이유 >
- 샘플링이 쉬움: q(z)는 단순 형태(가우시안 분포)를 사용하므로 샘플링이 쉽고 효율적
- 복잡한 계산 회피: z에 대한 직접적인 적분 대신, q(z)로부터 샘플을 생성해 평균을 계산하는 방식으로 복잡한 계산을 피할 수 O
- 근사 정확도 조정 가능: q(z)를 잘 설계하면 p(x)를 더 정확하게 근사할 수 O
그래서 p(x)를 최대화하려면, q(z)로부터 샘플링된 z에 대해 다음값을 최대화하면 됨
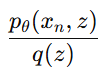
But, 우리가 실제로 최대화하려는 것은 관찰 데이터 xn에 대한 로그 가능도(log-likelihood)
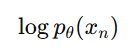
-> 직접적으로 계산은 어려우므로 이를 근사적으로 최적화하기 위해 ELBO 도입
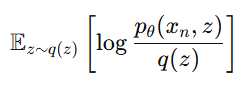
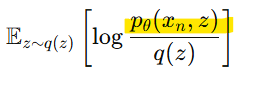
-> 결합 확률 p(x,z)를 조건부 확률로 분리
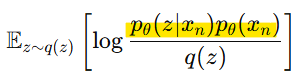
-> 로그의 곱셈을 분리
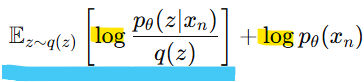
-> 첫번째 항은 KL발산의 정의에 따라 다음처럼 나타낼 수 O
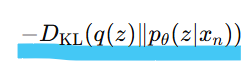

정리하면

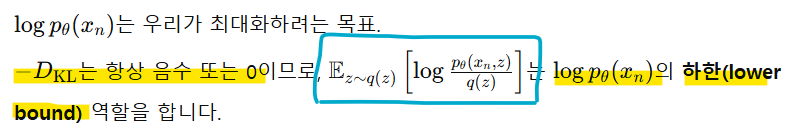
- Lower Bound(하한): 어떤 값을 직접 계산하기 어렵거나 최적화하기 어려운 경우, 해당 값을 근사적으로 추정할 수 있도록 돕는 안전한 하한선

-> ELBO를 최대화하면 logp(x)에 가까워짐
-> 즉, ELBO를 최대화하는 것 -> 로그 가능도를 최대화하는 간접적인 방법
-> KL 발산이 0에 가까워지면 ELBO는 logp(x)에 도달하고, q(z)와 p(z|x)가 더 가까워짐
-> 즉, q(z)는 latent 변수 z에 대한 사후 분포 p(z|x)를 잘 근사하게 됨
-> logp(x)를 직접 계산하기 어려우니 계산 가능한 ELBO를 도입하여 학습 가능하게 함
-> Lower Bound는 항상 실제 목표 값(logp(x))보다 작거나 같으므로, 최적화를 수행하면서 목표에서 멀어지지 않으므로 안전함
<ELBO를 최대화하면>
1) KL 발산 최소화: q(z)와 p(z|x)를 정렬(alignment)하여 두 분포를 더 가깝게 만듦
2) 로그 가능도 근사: KL 발산이 작아지면서, ELBO는 logp(x)에 더 가까워짐
- q(z|x)를 파라미터화하기
: 기존에는 q(z|x)를 잠재 변수 z의 임의 분포로 둠
이를 파라미터화된 함수로 설정
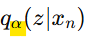
𝛼: 𝑞의 파라미터
𝒒𝜶(𝒛|𝒙𝒏): 데이터 xn에 대해 latent 변수 z의 분포
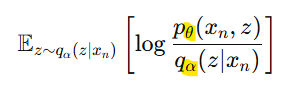
-> 이제 모델의 파라미터 𝜽와 𝒒𝜶(𝒛|𝒙𝒏)의 파라미터 𝜶를 동시에 최적화함

1) 𝐥𝐨𝐠𝒑𝜽(𝒙𝒏) 최대화
2) 𝒒𝜶(𝒛|𝒙𝒏)를 𝒑𝜽(𝒛|𝒙𝒏)와 비슷하게 함
<파라미터화된 𝒒𝜶(𝒛|𝒙𝒏)의 이점>
- 더 유연한 근사 분포: 𝒒𝜶(𝒛|𝒙𝒏)를 신경망 같은 복잡한 함수로 파라미터화하면, 단순한 정규분포보다 훨씬 유연하게 𝒑𝜽(𝒛|𝒙𝒏)를 근사할 수 O
- 효율적 학습: 𝛼를 포함한 최적화는 𝒒𝜶(𝒛|𝒙𝒏)를 계속 업데이트하며, 데이터에 더 적합한 잠재 분포를 학습함
- 변분 추론 자동화: 복잡한 모델에서도 자동으로 근사 분포를 학습할 수 있어, 수작업으로 분포를 설계할 필요가 감소
<𝒒𝜶(𝒛|𝒙𝒏)의 역할 = 인코더와 유사함>
- 관찰 데이터 xn에서 잠재 변수 z를 추출하는 역할
-> 인코더와 마찬가지로, 𝒒𝜶(𝒛|𝒙𝒏)는 z가 xn로부터 잘 decoding될 가능성을 최대화해야 함
- 𝒒𝜶(𝒛|𝒙𝒏)를 가우시안 분포로 모델링
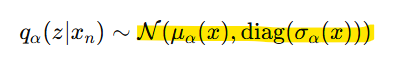

-> 계산이 간단, 효율적 + 분포가 연속적이라 latent space에서 샘플링이 용이
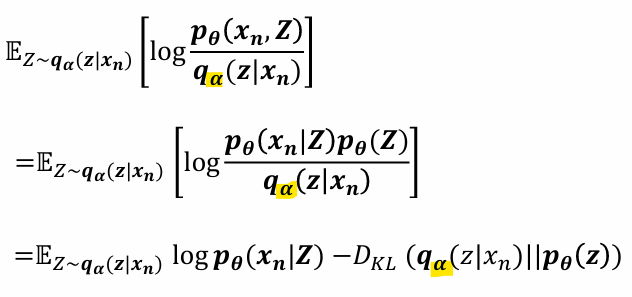
- 최종 Loss

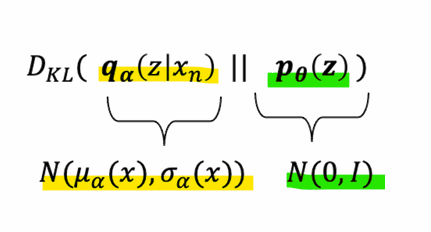
- 다차원 가우시안 분포 간 KL 발산 계산 공식
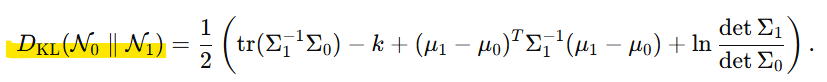

위 공식에 분포들을 대입하면

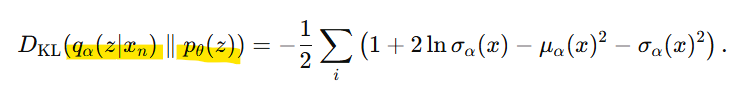
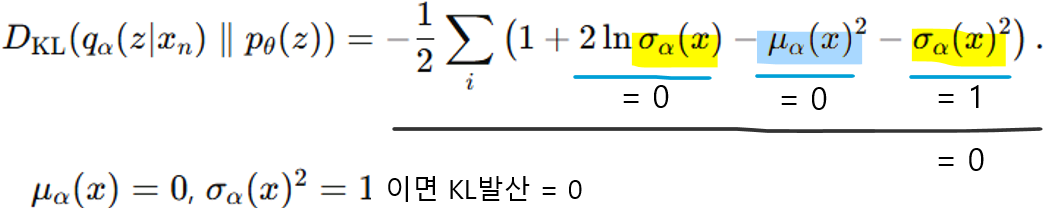


- Reconstruction Loss(두번째 항)

- Reparameterization Trick(재파라미터화 트릭)
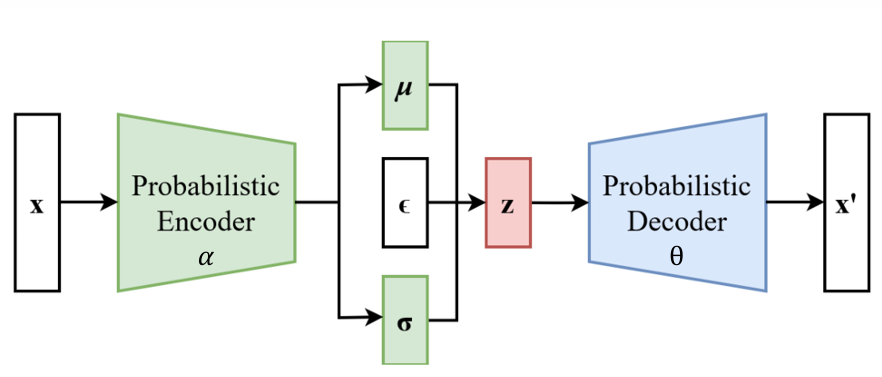
-> z의 샘플링을 평균(mean)과 표준편차(std)를 사용하여 구현하면, 확률적 변수의 샘플링을 미분 가능하게 만들어서 alpha or theta에 대한 gradient를 계산할 수 있음. 신경망의 학습에서 사용됨
<확률적 샘플링의 문제점>
: 확률적 모델(ex. VAE)에서 잠재 변수 z를 샘플링 시,

-> 이 방식은 샘플링이 확률적(랜덤)이므로 역전파를 통한 학습 과정에서 미분이 불가능함
<해결책: 재파라미터화 트릭>
: 확률적 샘플링을 분리하여 미분 가능하게 만드는 방법
1) 랜덤성은 고정된 분포(예: 표준 정규분포 N(0,1))에서 샘플링
2) 평균과 표준편차를 통해 샘플링된 값을 변환
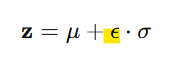

-> 이 방식은 랜덤성(ϵ)을 분리하여, μ와 𝜎에 대한 경사 하강법을 적용할 수 있게 함!(학습 가능해짐)
-Pytorch 코드:

- Latent Representation
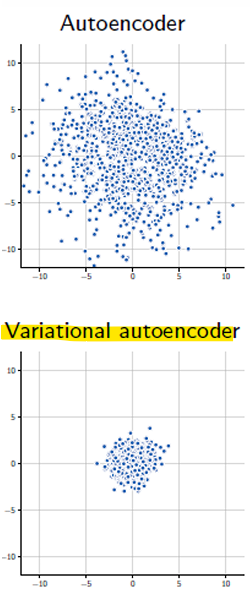

<장점>
- 생성 능력 (Generative capabilities)
: 학습된 잠재 공간(latent space)에서 샘플링함으로써 새로운 데이터를 생성할 수 있음
: 인코딩 과정의 확률성을 통해 재구성 결과에 다양성을 부여할 수 있음
- latent space: 데이터를 압축하거나 요약한 표현이 위치하는 공간
- latent variable: 잠재 공간의 벡터
-
구조화된 잠재 공간 (Structured latent space)
: VAE는 연속적이고 구조화된 잠재 공간을 강제하여, 데이터 간의 부드러운 보간(smooth interpolation)을 가능하게 함
: 스타일 변환(style transfer)과 같은 응용 분야에서 유용 -
KL 발산을 통한 정규화 (Regularization via KL divergence)
: KL 발산은 더 일반화된 표현을 학습하도록 유도하여 과적합(overfitting)을 방지하고 모델의 견고성(robustness)을 향상
-> 잠재 공간(latent space)을 원하는 분포(일반적으로 표준 정규 분포 N(0,1))에 맞게 정렬(alignment)시키기 때문
- Application: Autoencoder for LDM(Latent Diffusion Model)
1) VAE of Stable Diffusion
: VAE를 통한 이미지 representation 정규화
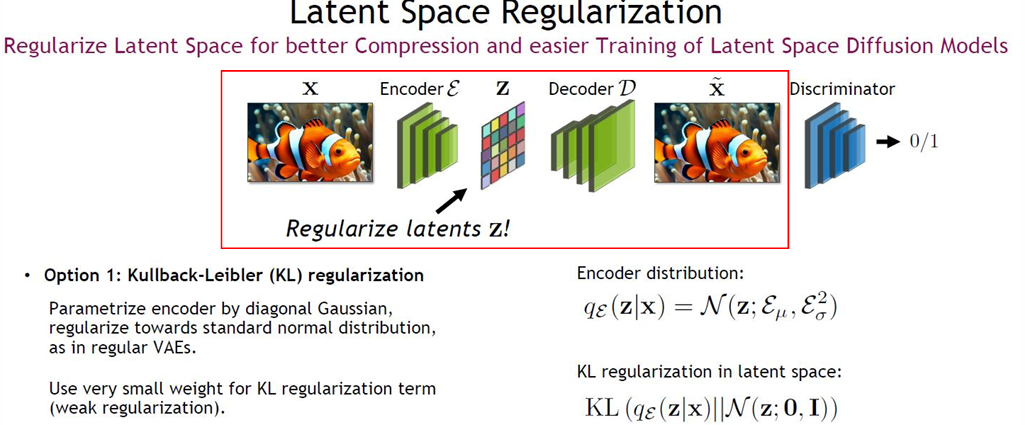
2) Stable Diffusion의 잠재 확산(Latent Diffusion)
: 조건부 정보를 기반으로 잠재 표현(latent representation)을 생성
-> 데이터를 직접 다루는 대신, 데이터를 잠재 공간(latent space)으로 변환하여 효율적으로 학습하고 생성 과정을 수행하는 방법
- Target representation: VAE의 잠재 표현(latent representation)
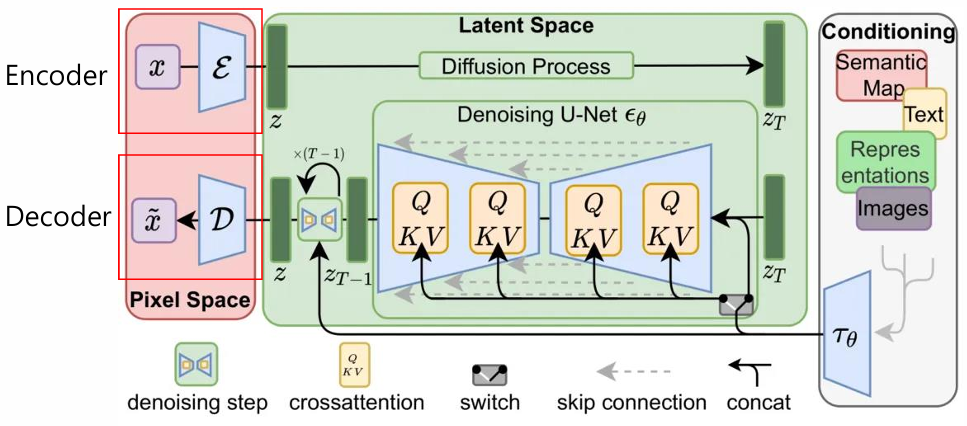
<LDM의 구조>
1) 인코더 (Encoder)
고차원 데이터를 저차원의 잠재 공간으로 변환
예: 512x512 크기의 이미지를 잠재 공간에서 64x64 크기의 표현으로 압축
2) Diffusion Model
잠재 공간에서 노이즈를 점진적으로 제거하거나 추가하며 데이터를 생성
학습 과정에서 잠재 표현이 노이즈로 오염된 후, 이를 원래 데이터에 가깝게 복원하도록 학습
3) 디코더 (Decoder)
잠재 표현을 다시 고차원 데이터(이미지, 오디오 등)로 복원
디코더는 데이터의 품질을 결정하는 중요한 요소
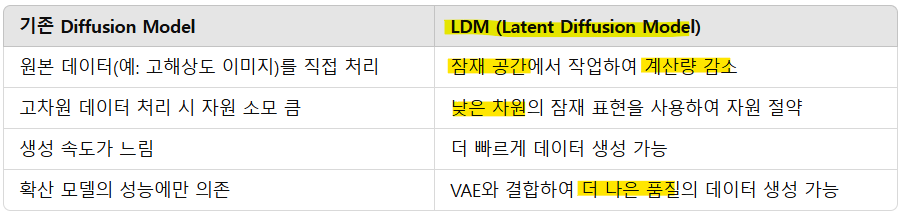
- Make-an-Audio의 VAE
- Make-an-Audio: 텍스트, 이미지를 오디오로 변환하거나 오디오 자체를 생성하는 생성 모델
: VAE를 통해 오디오 representation을 정규화
-> 오디오 데이터를 직접 처리하면 계산량이 크기 때문에, VAE를 사용해 오디오 데이터를 잠재 공간으로 압축하여 효율적으로 처리
-> 잠재 공간이 정규화되어 있어, 잠재 표현에서 생성된 오디오가 자연스럽고 일관성 있게 들림

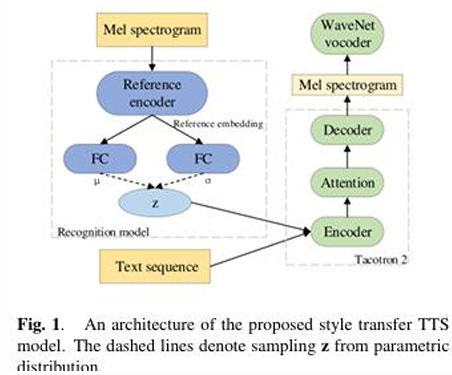
- Application: VAE-based Style Controllable Text-to-Speech
- VAE + Tacotron2
: 종단간 음성 합성에서 스타일 제어 및 전이에 대한 잠재 표현 학습
- Style Control and Transfer
: reference audio에서 화법 스타일을 생성
: VAE를 통해 latent representation을 샘플링
: text representation과 style representation을 디코더에 입력하기 전에 결합
- Visualization of Latent Representation
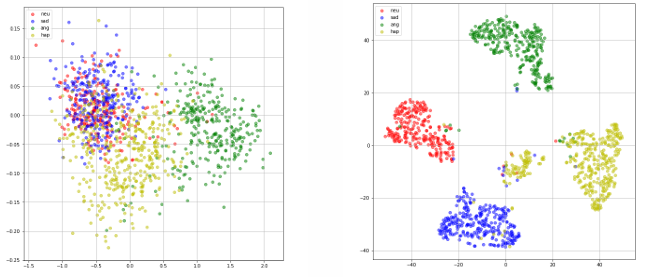
- Left: 각 latent representation(감정 별로)은 거의 가우시안 분포를 따름
- Right: latent representation의 T-SNE 결과
Reconstruction loss는 데이터의 중요한 특징을 잠재 표현(latent representation)에 반영하도록 학습을 유도
- T-SNE: 고차원 데이터를 저차원(보통 2차원 또는 3차원)으로 변환하여 시각화하는 데 사용되는 비선형 차원 축소 기법. 데이터의 국소적인 구조(local structure)를 보존하면서, 데이터 포인트 간의 관계를 이해하기 쉽게 함
- 결론
-
VAEs는 잠재 공간(latent space)에 구조를 부여하도록 설계되었으며, 이는 모델의 일반화 능력을 향상시키고 더 세밀한 표현을 생성할 수 있도록 도움
-
VAE는 모델의 제어 가능성(controllability)을 개선할 수 있음
-
VAE는 데이터의 계산 불가능한 주변 로그 가능성(marginal log-likelihood)을 근사하는 변분 하한(ELBO)을 최대화하도록 최적화됨
-> 모델을 학습시키려면 음의 ELBO(negative ELBO)를 최소화하면 됨
-> 손실(Reconstruction Loss와 KL Loss)을 최소화하여 학습
