회귀(Regression)

ROK·2022년 1월 29일

AIFFEL Cross Entropy Regression softmax 로지스틱 회귀 분석 선형 회귀 아이펠 회귀

AIFFEL

목록 보기

14/17

지도학습의 경우 문제가 두 가지 분류(Classification)와 회귀(Regression) 문제로 나뉜다.

분류는 입력 데이터의 특성(feature)을 이용해 해당 데이터의 클래스(label)를 추론하는 것
회귀는 입력 데이터의 특성(feature)을 통해 연관된 다른 데이터의 정확한 값을 추론하는 것

분류의 경우 클래스를 추론하는 문제로 출력값은 클래스에 대한 확률이지만, 회귀의 경우 출력값은 종속변수에 대한 예측 값이다. 간단하게 말하면 회귀는 숫자 값을 출력하고, 분류는 문자 값을 출력한다

회귀 분석이란

회귀분석(Regression Analysis)이란 독립변수가 종속변수에 미치는 영향을 파악하고, 이를 통해 독립변수의 일정한 값에 대응하는 종속변수의 값을 예측하는 모형을 산출하는 방법이다.

독립변수란

실험에서 실험자가 직접 변경하는 변수, 수학에서 $x$ 로 표기한다.

종속변수란

독립변수의 값이 변함에 따라 달라지는 변수, 수학에서 $y$ 로 표기한다.

일반적으로 $y = ax + b$ 를 생각하면 된다. 이를 선형회귀에서는 단순 선형 회귀 분석이라고 하고, 독립변수가 무수히 많이 있을 경우에 $y = a_1x_1 + a_2x_2 + a_3x_3 + \dots + a_nx_n + b$ 과 같은 방정식을 다중 선형 회귀 분석이라고 한다.

간단하게 생각하면 독립변수에 따른 종속변수의 인과관계를 파악하는 분석이라고 생각해도 된다.
이는 데이터를 기반으로 연속형 변수 간의 관계를 모델링하고 이에 대한 적합도를 측정하는 분석방법이다.

간단하게 예를 들면

부모의 키와 자식의 키 관계
자동차의 스펙을 이용한 가격 예측
1인당 국민 총 소득과 배기가스 배출량 사이의 관계 예측

선형회귀분석(Linear Regression)

선형 회귀 분석은 회귀 분석의 대표라고 할 정도로 기본 중의 기본이다. 이름 그대로 선형 회귀는 종속변수와 한 개 이상의 독립변수와의 선형 상관관계를 모델링하는 회귀분석 기법이다.

위에서 설명했듯이 선형회귀식은 $y = ax + b$ 로 표현할 수 있는데, $a$ 는 회귀계수이고, $b$ 는 종속변수와 독립변수의 오차를 의미한다. 이 값들은 데이터로부터 추정해야하는 파라미터이다.

작동 순서는 아래와 같은 순서를 가진다.

$x, y$ 데이터가 있을 때, 이 데이터들을 통해 $a, b$ 를 추정

추정한 값들로 모델링을 수행

해당 모델을 사용해 $x$ 값을 입력하면 $y$ 값을 예측

결론적으로 주어진 데이터를 모델링한 선형식에 적절한 회귀계수 및 오차를 구하는 것이다.

머신러닝에서 선형회귀모델 표기법

머신러닝에서는 선형회귀모델을 다른 변수값을 통해 표현한다.
$H = Wx + b$
$H$ 는 가정(Hypothesis), $W$ 는 가중치(Weight), $b$ 는 편향(bias)이다.

변수만 다르지 구해내는 값과 순서는 동일하다.

오차(Error)와 잔차(Residual)

오차는 친숙한 말이지만 잔차는 낯선 용어일 것이다. 오차와 잔차를 비교해보며 차이점을 알아보자, (오차와 잔차는 완전 다른 값이다)

결론부터 말하자면

오차 : 모집단의 회귀식에서 예측한 값 - 실제 데이터 값
잔차 : 표본집단의 회귀식에서 예측한 값 - 실제 데이터 값

간단하게 오차와 잔차는 모집단을 기준으로 하는지 표본집단을 기준으로 하는지가 오차와 잔차의 차이점이다.

잔차는 회귀모델을 이용해 추정한 값과 실제 데이터 값의 차이인데, 예를 들어 선형회귀모델의 식이 $y = 2x + 3$ 이고 실제 데이터는 $(3, 10)$ 일 때, 잔차 값은 $10 - 9 = 1$ 의 값이 나온다. (10 = 실제 데이터 값, 9 = 선형회귀모델에 대입해서 나온 예측값)
이러한 잔차를 이용해 데이터들을 잘 설명하는 회귀 모델을 찾는 방법 중 하나가 최소제곱법이다.

최소 제곱법은

$\displaystyle\sum_{i=1}^{n} residual^2$
$\displaystyle\sum_{i=1}^{n}(y_i - f(x_i,\beta)^2$
$f(x_i, \beta) = ax_i + b$
$\beta$ 는 상수

위 식에서 n개의 입력 데이터에 대해 잔차의 제곱의 합을 최소로 하는 $\beta$ 값을 구하면 된다.

참고

최소제곱법과 같은 회귀계수를 구하는 함수를 손실함수(Loss Function)이라고 한다.
손실함수는 여러가지가 있지만, 이번엔 최소제곱법만 사용해본다

또한 회귀모델이 잘 됐는지 확인할 때 참고하는 지표는 결정계수(R-squared or R2 score)가 있다. 이는 0~1 사이의 값으로 표현하는데 1에 가까울수록 회귀 모델이 데이터를 잘 표현했다고 볼 수 있다.

모집단과 표본집단

모집단 : 정보를 얻고자 하는 전체 대상 또는 전체 집합

표본집단 : 모집단으로 추출된 모집단의 부분 집합

예를 들어 20대 남성과 30대 남성의 키를 비교한다고 했을 때, 모집단은 20대, 30대 남성 전체의 키가 된다. 실질적으로 20~30대 남성 모두의 키를 재는 것은 무리기 때문에 두 모집단에서 약 1000명씩 뽑아 비교하는 방법을 사용할 수 있다. 이때 각 1000명이 모집단을 대표하는 표본집단이라고 한다.

코드로 확인하기

실제 코드를 통해 선형회귀를 확인해보자.
Boston dataset을 통해 각 특성(feature)의 선형 회귀 모델을 구하고, 이 모델의 결정계수를 확인해보자

from sklearn.datasets import load_boston
from sklearn.model_selection import train_test_split
import pandas as pd
import numpy as np

boston = load_boston()
data, price = boston['data'], boston['target']
x_train, x_test, y_train, y_test = train_test_split(data, price, test_size=0.2, random_state = 10)

df = pd.DataFrame(x_train, columns=boston['feature_names'])
print("boston dataset의 차원 : ", data.shape)
print("price의 차원 : ", price.shape)
print("boston train dataset의 차원 : ", x_train.shape)
print("boston test dataset의 차원 : ", x_test.shape)

print("Boston dataset의 예시")
df.head()

출력값을 확인해보면 Boston dataset은 506 rows, 13 개의 feature로 구성되어 있다.
우리가 맞추려고 하는 정답(label)은 가격으로 price에 따로 저장되어 있다.

각 특성에 대한 정보는

print(boston["DESCR"])

을 확인하면 각 특성에 대한 설명이 나온다

이제 Boston Dataset에 선형회귀(Linear Regression)을 적용해볼 차례이다.

import pandas as pd
from sklearn import datasets
from sklearn.model_selection import train_test_split
from sklearn.linear_model import LinearRegression
from sklearn import metrics
import matplotlib.pyplot as plt

fig = plt.figure(figsize=(10,35))
fig.suptitle('Boston dataset = (X:Y = each attr: price) with R2', fontsize=16, y=0.9)

# boston dataset에서 i번째 attribute(column) 확인하기
for i in range(data.shape[1]):
    # i번째 attribute에 대한 data 및 이름
    single_attr, attr_name = data[:, i].reshape(-1, 1), boston['feature_names'][i]
    # 선형회귀모델
    estimator = LinearRegression()

    # x에 single_attr, y에는 price에 해당하는 데이터 대입 최소제곱법을 사용해 W, b 구하기
    estimator.fit(single_attr, price)

    # fit으로 구한 회귀계수 기반 회귀모델이 X값 대입했을 때 예측한 Y값 확인
    pred_price = estimator.predict(single_attr)

    # 결정계수 구하기
    score = metrics.r2_score(price, pred_price)

    # 그래프 그리기
    graph = fig.add_subplot(7, 2, i+1)
    graph.scatter(single_attr, price) # 실제 데이터 산포도
    graph.plot(single_attr, pred_price, color='red') # 선형회귀모델 추세선
    graph.set_title("{} x price, R2 score={:.3f}".format(attr_name, score))
    graph.set_xlabel(attr_name)
    graph.set_ylabel('price')

각각 13개의 속성마다 그래프를 하나씩 그렸다. 13개 중 결정계수(R2 score)가 높은 LSTAT, RM을 이용해 그린 선형회귀모델이 그나마 데이터를 잘 설명한다고 볼 수 있다.

로지스틱 회귀분석(Logistic Regression)

일상속에는 두 개의 선택지 중에서 정답을 골라야 하는 문제가 많다. 예를 들어 메일함에 스팸메일인지 분류하는 문제와 같이 Yes or No 둘 중 하나를 선택해야 하는 문제가 많다. 이와 같이 둘 중 하나를 결정하는 문제를 이진 분류(Binary Classification)이라고 한다.
로지스틱회귀는 이진분류를 해결하는 대표적인 알고리즘이다.

로지스틱 회귀분석은 데이터가 어떤 범주에 속할 확률을 0~1 사이의 값으로 예측해 확률에 따라 분류해주는 지도 학습 알고리즘이다.

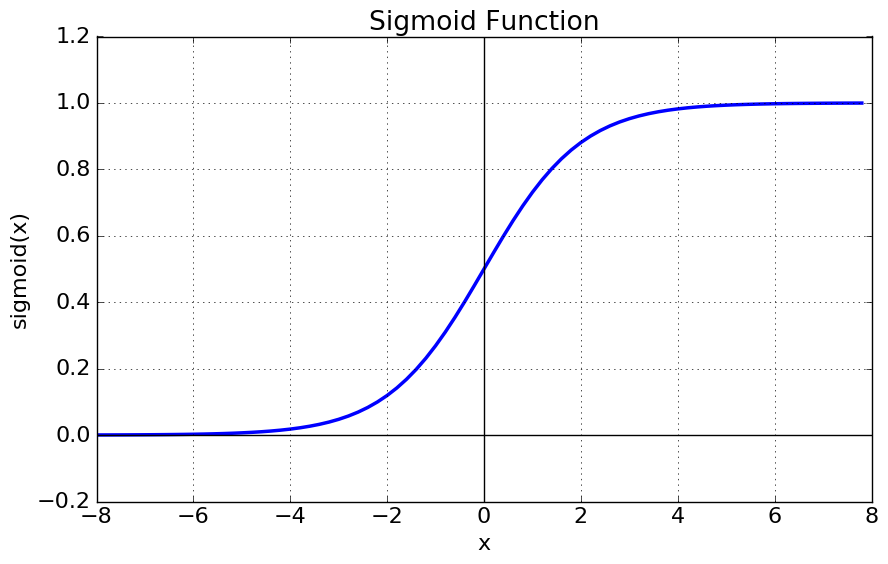
로지스틱 회귀분석에 가장 적절한 함수는 시그모이드 함수(Sigmoid Function)이다.

시그모이드 함수(Sigmoid Function)

시그모이드 함수는 출력이 0~1의 값을 가지면서 S자 형태를 그리는 함수로 아래 그림과 같다.

오즈 비(odds ratio)

시그모이드 함수는 오즈 비(odds ratio)라는 통계를 기반으로 만들어진 함수이다.
오즈 비는 성공 확률과 실패 확률의 비율을 나타내는 통계로 아래와 같이 정리한다

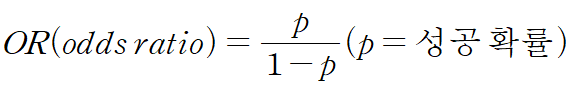
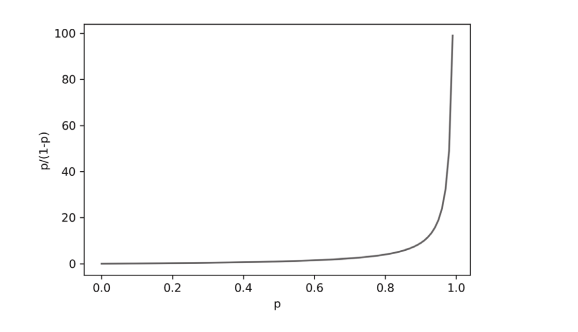
p가 0에서 1까지 증가할 때 오즈 비 값은 천천히 증가하다 p가 1에 가까워지면 급격히 증가한다.

로짓 함수(logit function)

오즈 비에 로그를 취하여 만든 함수를 로짓 함수(Logit Function)라고 한다.

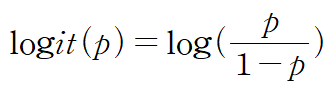
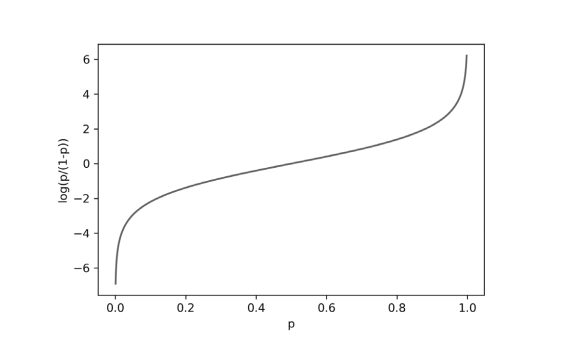
로짓 함수는 p가 0.5일 때 0이 되고, p가 0, 1 일 때 무한대에 가까워진다.

세로 축을 z, 가로 축을 p로 놓으면 확률 p가 0에서 1까지 변할 때 z가 매우 큰 음수에서 매우 큰 양수까지 변하는 것으로 생각할 수 있다. 이를 표현한 것이 아래와 같은 식이다.

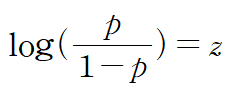
로지스틱 함수(logistic function)

위 식을 z에 대하여 정리하면 아래와 같은 식이 나오게 된다. (z에 대해 정리하는 이유는 z를 가로축으로 놓기 위해서이다)

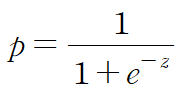
시그모이드 함수는 그래프로 그렸을 때 로짓함수에서 가로 축과 세로 축을 반대로 뒤집은 모양으로 S자 형태를 가진다. 이 모양으로 인해 시그모이드 함수라고도 한다.

코드로 확인하기

유방암 데이터셋을 사용해 로지스틱 회귀분석 예시를 살펴보자

from sklearn.datasets import load_breast_cancer
from sklearn.model_selection import train_test_split
import pandas as pd

# 데이터 로드
cancer = load_breast_cancer()

cancer_data, cancer_target = cancer.data, cancer['target']

# 데이터 분류 y가 0일때 악성 종양, 1일때 양성 종양
x_train, x_test, y_train, y_test = train_test_split(cancer_data, cancer_target, test_size=0.2, random_state=10)
print("전체 검사자 수 : ", len(cancer_data))
print("특성 수 : ", len(cancer_data[0]))
print("Train dataset에 사용되는 검사자 수 : ", len(x_train))
print("Test dataset에 사용되는 검사자 수 : ", len(x_test))
cancer_df = pd.DataFrame(cancer_data, columns=cancer['feature_names'])
cancer_df.head()

데이터를 모두 준비했으니 로지스틱 회귀분석 모델에 적용해보자

from sklearn.linear_model import LogisticRegression
from sklearn.metrics import classification_report

lr = LogisticRegression()
lr.fit(x_train, y_train)
lr_pred = lr.predict(x_test)

# 회귀분석 모델 예측값과 실제값 비교
print(classification_report(y_test, lr_pred))

로지스틱 회귀는 회귀인가?, 분류인가?

로지스틱 회귀는 이름은 회귀 지만 방금 사용한 예시는 유방암 데이터셋의 이진 분류 문제였다.

로지스틱 회귀는 회귀가 맞다. 다만 선형 회귀 방식을 분류에 적용한 알고리즘이다.

로지스틱 회귀는 독립변수가 아닌 가중치(Weight)가 선형인지 아닌지에 따라 회귀의 선형, 비선형을 결정한다. 일반적인 회귀 모델은 오차제곱합(SSE)을 최소로 갖는 회귀선을 찾지만 로지스틱 회귀분석은 시그모이드 함수 최적선을 찾아 시그모이드 함수의 반환 값을 확률로 간주하여 분류를 진행한다.

로지스틱 회귀는 분류 문제를 확률적으로 접근하는 핵심 아이디어를 제공하기 때문에 기억해두는 것이 좋다

ROK

하루에 집중하자

이전 포스트

AI, 딥러닝, 머신러닝

다음 포스트

회귀(Regression)

AIFFEL

회귀 분석이란

독립변수란

종속변수란

선형회귀분석(Linear Regression)

머신러닝에서 선형회귀모델 표기법

오차(Error)와 잔차(Residual)

코드로 확인하기

로지스틱 회귀분석(Logistic Regression)

시그모이드 함수(Sigmoid Function)

오즈 비(odds ratio)

로짓 함수(logit function)

로지스틱 함수(logistic function)

코드로 확인하기

로지스틱 회귀는 회귀인가?, 분류인가?

AI, 딥러닝, 머신러닝

텍스트 요약

0개의 댓글