Bias, Variance

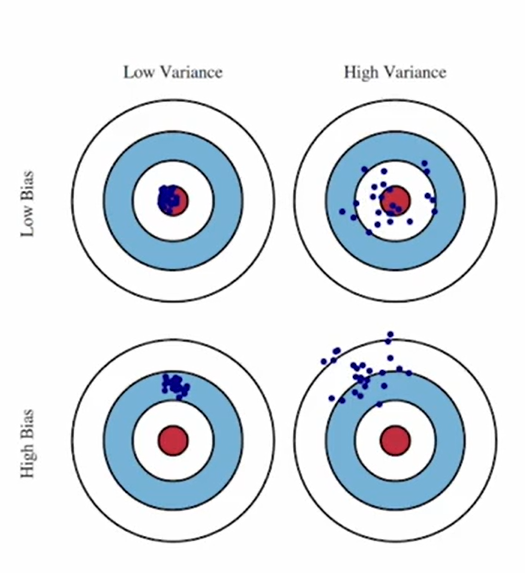
1. Bias

$E(\hat{h} - f)$

Estimation(Trained model)과 True data distribution 차이의 평균치
모델의 가정 자체가 실제 데이터 분포가 다른 정도

• Bias가 큰 모델은 아무리 잘 학습하더라도 true distribution을 정확하게 추정할 수 없음
  • 모델 파라미터 수가 적을수록 bias는 커짐
    - 파라미터 수가 적을 때는 모델이 복잡한 패턴을 충분히 학습할 수 없으므로, 간단한 패턴만 학습하게 됨
    - 파라미터 수 ⇒ 모델의 표현력
    
    

2. Variance (=Complexity)

Estimation의 분산
샘플링에 따라서 모델의 파라미터가 얼마나 민감하게 변하는 지
모델이 지나치게 민감해서 노이즈까지 학습한 것

• Variance가 큰 모델은 샘플링된 데이터가 true distribution을 잘 반영하지 못 한다면 true distribution을 정확하게 추정할 수 없음
  • 모델 파라미터 수가 많을수록 variance는 커짐
  • 학습 데이터 수가 적을수록 variance는 작아짐
• Variance를 줄이는 가장 안전하고 효과적인 방법 : 학습 데이터셋의 크기를 늘리는 것!
  
  

3. Bias Variance trade-off

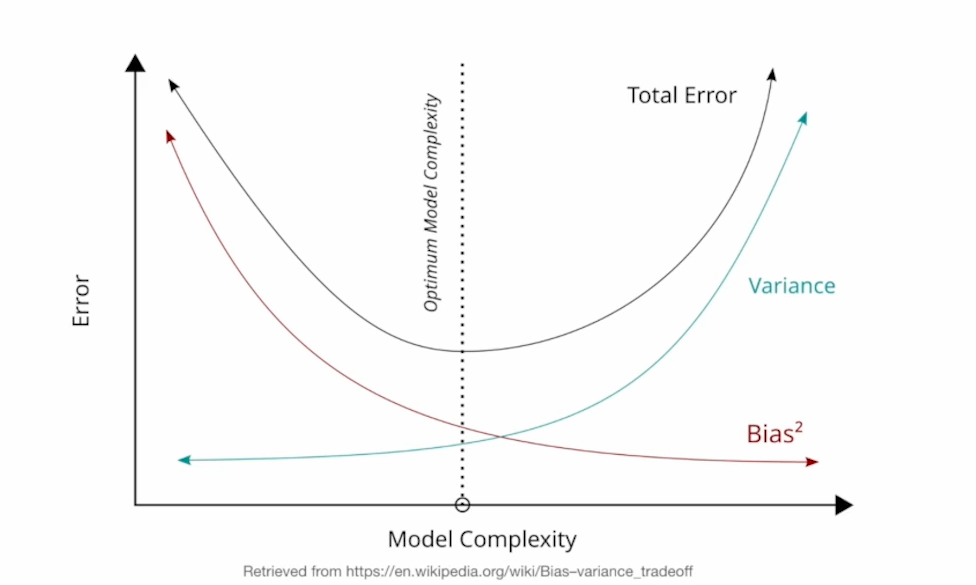
단순히 bias, variance를 임의로 늘리고 줄이는 것으로 최적의 모델을 찾을 수는 없으므로 데이터의 특성을 신중하게 고려해야 함

• Inductive Bias : 데이터의 특성을 고려해 모델에 추가적인 가정을 넣는 것

  • 예) 이동거리가 $x$, 택시비가 $y$일 때, $h(x) = ax + b$와 같이 식을 세울 수 있음
    그러나 이동거리가 0이면 택시비도 당연히 0이기 때문에 $b = 0$이라는 가정을 추가(bias의 증가)할 수 있음
    → 데이터의 특성을 고려한 가정이기 때문에, bias가 증가해도 모델의 성능을 해치지 않음