CNN(Convolutional Neural Network) basic

1. MLP의 한계

• 구조적 한계
  • MLP(fully-connected)는 층이 깊어지고 뉴런의 수가 많아지면 가중치 수가 급격히 늘어남
  • 이는 학습해야 할 매개변수의 수가 많아져 오버피팅의 위험이 커지고, 계산 복잡도가 증가하는 한계가 됨
• 위치 민감성
  • MLP는 이미지의 특정 패턴의 위치에 민감함
    • 즉, 인풋 이미지의 모든 정보를 일차원 벡터로 변환해 처리하기 때문에, 패턴의 위치에 종속된 결과를 내게 됨
  • 이는 이미지에서 패턴이 어디에 위치해 있는지에 따라 결과가 달라질 수 있음을 의미하며, 이미지의 위치 불변성을 보장하지 못 함
• 패턴의 차이
  • MLP는 입력을 일차원 벡터로 변환해 처리하기 때문에, 이미지에서 같은 숫자 '5'라도 위치나 크기가 조금만 달라져도 다른 숫자로 판단할 수 있음
• 크기 조절의 필요성
  • 이미지 인식에서 패턴이 위치나 크기에 따라 인식 결과가 달라질 수 있기 때문에, MLP로 숫자를 인식하려면 숫자의 크기와 위치를 비슷하게 맞추는 전처리가 필요함
    
    

2. CNN의 등장

• 1980년대 Kunihiko Fukushima의 Neocognitron이라는 신경망에서 CNN 기초 개념 유래되었음. 이는 계층적 구조를 통해 시각적 패턴을 인식할 수 있는 신경망이었으며, 이는 뒤이어 나올 CNN의 발전에 큰 영향을 미쳤음
• 1998년 Yann LeCun 교수가 LeNet 발표
  • 그 중 LeNet-5는 1998년 발표된 CNN 모델로, 숫자 필기체를 인식하는 문제에서 큰 성과를 보였음 (MNIST 데이터셋 사용)
  • LeNet-5는 현대적인 CNN의 원형으로, 컨볼루션 레이어와 풀링 레이어, 완전 연결층이 결합된 구조를 갖고 있으며, 오늘날 많은 컴퓨터 비전 응용에 사용되는 CNN 아키텍처의 기반이 되었음
    
    

3. CNN 개요

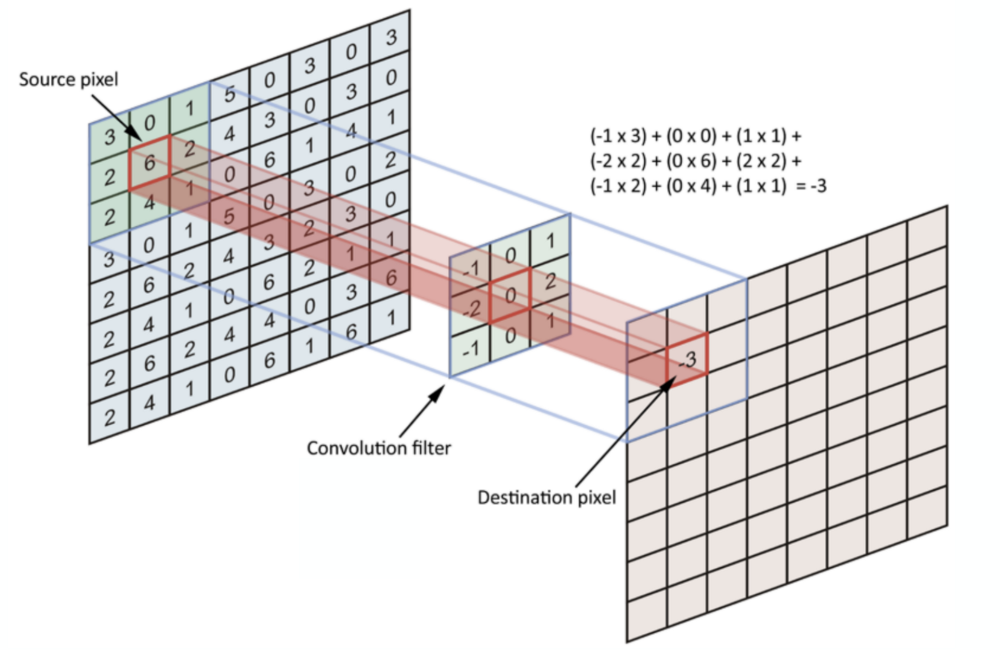
• MLP에서는 각 입력마다 다른 가중치들이 계산되며 적용되었는데, CNN에서는 계산을 효율적으로 만들기 위해 가중치 뉴런을 공유하는 방식(=필터 혹은 커널)을 사용함

• CNN(Convolution Neural Network, 합성곱) : 이미지에서 특징을 추출하기 위해 필터(= 커널, 마스크)를 사용하는 방법

  • 필터와의 합성곱을 통해 이미지의 특정 특징(엣지, 텍스처, 패턴 등)을 추출하며, 신경망이 이미지를 더 잘 이해하고 분류하도록 함
  • CNN은 학습을 통해 자동으로 적합한 필터를 생성함
  • 필터 종류 : 엣지 검출 필터(Sobel, Prewitt, Laplacian), 블러 필터, 샤프닝 필터, 가우시안 필터, 평균 필터 등 (필터 크기는 5×5나 7×7 등 임의의 크기로 설정 가능)

※ 이미지 크기는 (가로, 세로, 채널)로 표현됨

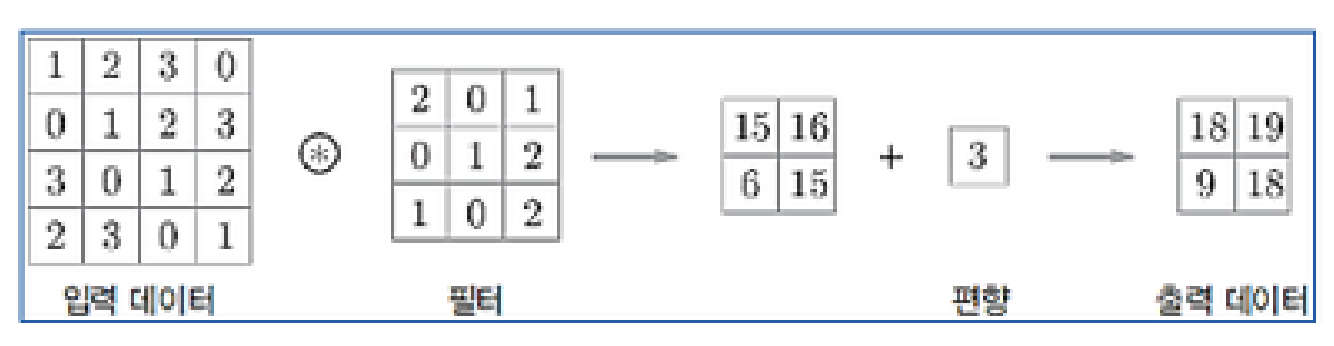
• 특성맵(Feature Map) : 합성곱 계층의 입출력 데이터로, 2차원 평면(채널)으로 구성됨 (입력의 각 위치에 필터가 적용되어 계산된 결과)
  • 필터의 개수는 모델 설계 시 학습할 피처 개수와 관련된 하이퍼 파라미터로, 직접 정하는 값임 (예, 필터 5개를 사용했다면 이미지에서 특징 5개 추출)
  • 필터가 이미지의 각 위치에서 계산된 결과가 모여 하나의 피처맵이 됨
  • 여러 필터를 사용하는 경우 각 필터는 독립적인 피처맵을 생성하며, 이 피처맵들이 쌓여 채널 방향으로 다음 레이어로 전달됨
  • 흑백 이미지(예, MNIST) 깊이는 1, RGB 이미지의 경우에는 3 ← 채널 을 말하는 것! (색상 정보)

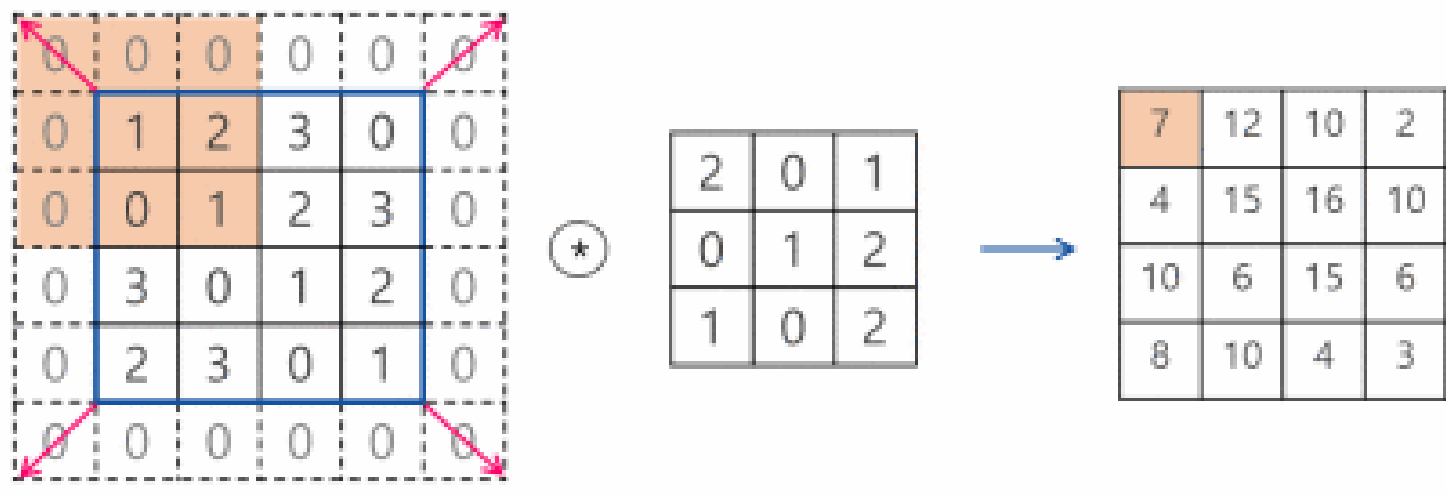
• 패딩(Padding) : 필터 크기로 인해 이미지 가장자리 부분 데이터가 부족해 입력과 출력 크기가 달라지는데, 이를 보정하기 위해 입력 신호의 가장자리 부분에 0을 미리 채워넣는 것
  • Conv2D 계층에서는 padding 파라미터를 사용해 패딩을 지정할 수 있음
    • valid : 패딩 사용 X (유효 영역만 출력하므로 출력 이미지 사이즈는 인풋 사이즈보다 작아짐)
    • same : 출력 차원이 입력과 같아지도록 적절한 수의 패딩을 자동으로 입력하는 것

• 축소 샘플링(subsampling) : 컨볼루션 결과에서 핵심적인 정보만 추출해 다음 레이어로 전달하는 과정
  • 필터 수를 늘리면 피처맵 개수가 커지게 되는데, 중요한 정보만 선택적으로 전달해 데이터 차원을 줄이고 모델의 복잡성을 감소시키는 역할을 함
  • 일반적으로 pooling과 stride를 통해 축소 샘플링을 구현함

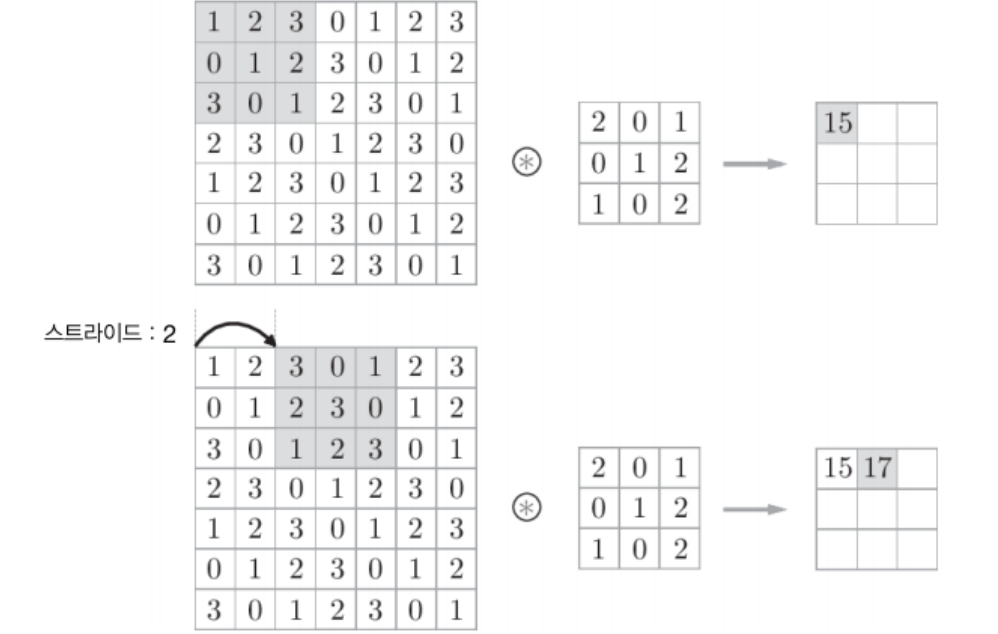
• 스트라이드(stride) : 컨볼루션 수행할 때 필터를(예, 3×3)를 한 픽셀씩 이동하지 않고, 여러 픽셀씩 건너 뛰면서 이동하며 출력 얻는 방법

  • 2-stride를 사용하면 필터를 두 픽셀씩 건너뛰며 이동함 (출력 피처맵 크기가 절반으로 감소)
  • 3-stride를 사용하면 세 픽셀씩 건너뛰며 이동해, 출력 크기가 1/9로 감소

• 풀링(pooling) : 컨볼루션 결과를 다음 레이어로 모두 전달하지 않고, 일정 범위 내에서(예, 2×2 픽셀 범위) 대표값을 선택해 전달하는 방법

  • Max Pooling : 특정 범위 내 최대값 선택 (대표 정보만 남기고 나머지 신호 제거함. 입력의 변화에 영향 적게 받음)
  • Average Pooling : 특정 범위 내 평균값 선택 (전체 정보를 고르게 반영하며, 평활하게 일반적인 정보 유지함)

4. CNN 아키텍처

🟠 요 약
Convolution Layer : 가중치 공유 → 파라미터 개수 감소, 계산량 감소
Pooling Layer : 이미지 크기 감소 → 파라미터 개수 감소, 계산량 감소

FCL 전 까지는 Feature Extractor, 이후로는 Classifier

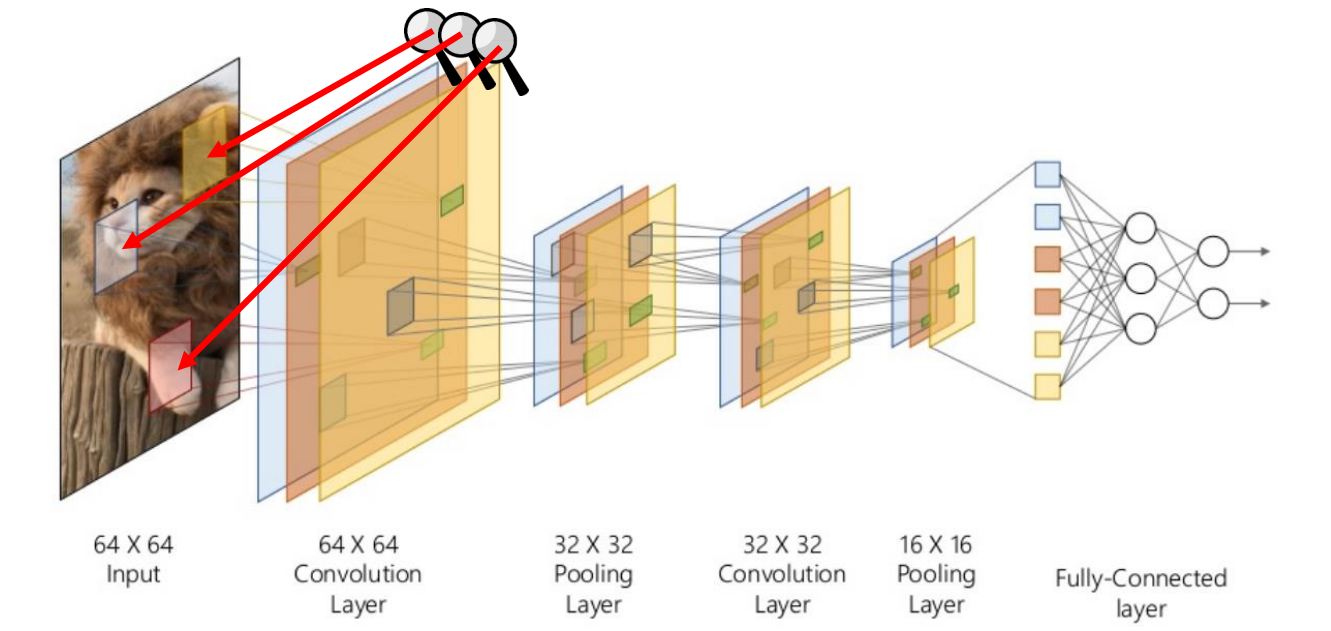
입력 이미지 → Conv+ReLU+Pooling → h(x)+ReLU → h(x) → Flatten → Fully Connected Layer → Softmax → 결과값

단 계	설 명
입력	네트워크에 이미지 (64, 64, 3) 입력
Conv + ReLU + Pooling	Conv : 이미지 특징을 추출 - 필터의 개수가 32개라고 가정하면 (64, 64, 32) ← 출력 이미지 채널 수가 필터 개수로 바뀜 ReLU : 비선형성 도입해 모델이 복잡한 패턴을 학습할 수 있게 함 Pooling : Max Pooling이나 Average Pooling을 통해 공간 크기 줄임 → (2×2) 필터 사용 시 (64, 64, 32)에서 (32, 32, 32)로 줄어듦
h(x) + ReLU	h(x) : Conv 레이어의 아웃풋 (32, 32, 32) ReLU : 비선형성 추가해 모델이 복잡한 패턴을 학습할 수 있게 함
h(x)	중간 출력 값으로서, 다음 단계로 전달됨 (32, 32, 32)
Flatten	h(x)를 1차원 벡터로 변환해 Fully Connected Layer에 입력할 수 있도록 함 - 출력 크기 (32*32*32,)
Fully Connected Layer	이전 단계의 특징 벡터를 입력으로 받아 전체 연결된 뉴런들로 변환해 더 복합적인 특징 학습함. 뉴런 수가 128이라면 출력 크기는 (128,)
Softmax	마지막 출력 레이어로, 클래스별 확률을 계산해 최종 (다중) 분류 수행함. 클래스 수가 10이라면 출력 크기는 (10,)
출력	Softmax 결과를 기반으로 예측된 클래스 혹은 확률값 산출

컨볼루션 레이어

• 이미지 전체에 걸쳐 동일한 가중치를(필터) 적용함으로써, 이미지 위를 슬라이딩하며 패턴을 인식함
  • 필터가 각 채널에 개별적으로 적용되는 것이 아니라, 입력의 모든 채널을 함께 고려해 특징을 추출하는 것
• 이 때, 동일한 가중치를 반복적으로 사용하기 때문에 파라미터 수가 줄어듦
  • 공간 크기는 그대로 유지되지만 채널 수는 필터 개수만큼 늘어남
• 각 필터는 입력 이미지의 채널을 합쳐 하나의 채널을 생성하기 때문에, 필터의 수가 곧 출력의 채널 수(피처맵의 개수)가 됨
  • 채널 수의 증가는 더 많은 필터를 사용해 각기 다른 특징을 학습하는 과정에서 발생함. 즉, 필터의 개수가 늘어날수록 출력 이미지의 채널 수가 증가하게 됨

풀링 레이어

• 공간 크기를 줄임으로써 연산량을 줄이고 오버피팅을 방지하며 중요한 특징만 남김
• 일반적으로 공간 크기(너비와 높이)를 줄이지만 채널 수는 유지함

✅ 컨볼루션 레이어에서 가중치를 공유함으로써 학습해야 할 파라미터 수가 감소하는 원리

• MLP의 FCL(은닉층, 출력층)에서는 입력의 모든 픽셀에 대해 각각의 뉴런이 별도의 가중치를 가짐. 즉, 모든 입력 픽셀과 뉴런이 서로 연결되기 때문에 매우 많은 수의 파라미터가 필요함
  • 예, 인풋 이미지 크기가 (32×32×3) = 총 픽셀 개수 3072개이며 뉴런의 개수가 100개라면, 각 뉴런은 3072개의 가중치를 가짐 (전체 3072 * 100 = 307200개의 가중치)
• 컨볼루션 레이어에서는 특정한 크기의 필터가 이미지의 전체 위치에 동일하게 적용됨 = 가중치 공유
  • 예, 필터 크기가 3×3이고 입력 채널 수가 3이라면, 필터 하나는 (3×3×3) = 27개의 가중치로 구성됨. 그리고 필터 개수가 32개라면 총 가중치 개수는 27*32 = 864개임
  • 이 필터는 이미지의 모든 위치에 반복적으로 적용되기 때문에, 각 위치에서 새로운 가중치를 학습할 필요가 없고 동일한 가중치를 적용해서 전체적으로 학습해야 하는 파라미터의 개수가 줄어듦

컨볼루션 레이어 예시 (Keras)

• 필터 적용
  • 인풋 이미지에 필터(커널)를 슬라이딩하며 컨볼루션 연산 수행
  • 각 필터는 입력 이미지의 각 위치에 해당하는 픽셀값과 자신의 가중치를 곱한 후, 그 결과를 모두 더한 값으로 피처맵의 한 픽셀값을 생성한
• 각 필터 별로 피처맵 생성
  • 하나의 필터는 인풋 이미지의 모든 채널에 대해 연산을 수행해 하나의 피처맵을 생성함
  • 여러 개의 필터를 사용하면 각각의 필터는 독립적인 특성맵을 생성함 (필터 개수만큼 피처맵이 생성되고 이 피처맵들이 합쳐져 출력이 됨)

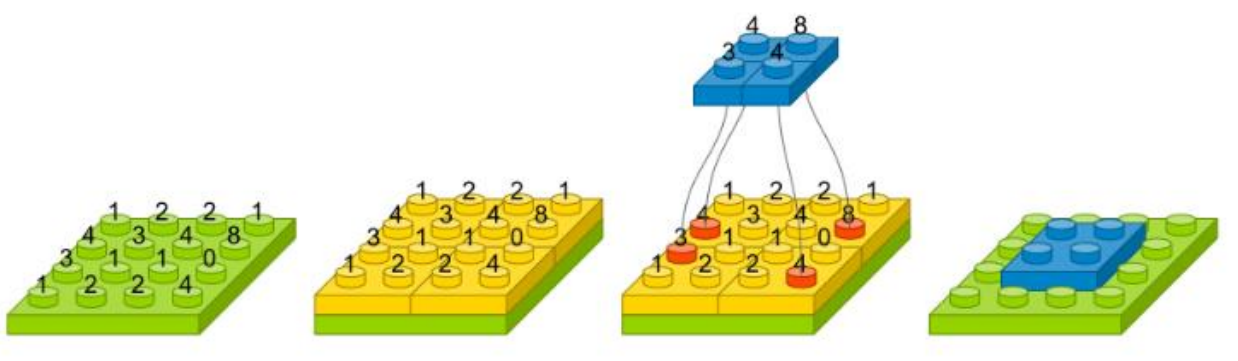
# 1
Conv2D(filters=3, # 컨볼루션 필터 개수
	   kernel_size=(2, 2), # 필터 크기
       padding='same', # 패딩 (인풋, 아웃풋 사이즈 동일)
       input_shape=(3, 3, 1), # 입력 이미지 크기

# 2
Conv2D(filters=1, 
	   kernel_size=(2, 2),
       padding='same', 
       input_shape=(3, 3, 3)) 

# 3
Conv2D(filters=2, 
	   kernel_size=(2, 2),
       padding='same', 
       input_shape=(3, 3, 3)) 

# pool_size, stride 파라미터 예시
MaxPooling2D(pool_size=(2, 2), stride=(2, 2))
# pool_size : 맥스 풀링 크기
# stride : 스트라이드 크기

• flatten() : 다차원 피처맵을 1차원 벡터로 변환하는 기능 (예, (8, 8, 32) → (8 * 8 * 32) = 2048
  • 1차원 벡터로 처리한 후 FCL에 전달해 최종 작업 수행

4-1. 오버피팅 방지 기법

참고링크 - github

• Early Stopping
• L1, L2 regularization
• Dropout : 학습 동안에만 적용되고 학습 종료 후 예측 단계에서는 모든 유닛을 사용함
• Data Augmentation
  • roation_range, width_shift_range, height_shift_range, shear_range, zoom_range, horizontal_flip, vertical_flip
• 가중치 초기값 설정 (Xavier 초기화, He 초기화)
  • 모델의 수렴 속도 및 학습 안정성을 위해 가중치를 적절히 초기화하는 것이 중요함
  • 적절한 가중치 초기화는 네트워크가 학습 초기에 활성화 함수의 기울기 소실이나 기울기 폭발 문제를 방지하게 해 줌 (특히 네트워크가 깊어질수록 중요)
  • 전 레이어 노드를 이용해 표준편차가 $1/\sqrt{n}$인 정규분포로 초기화하는 방법
  • 예, 입력 노드가 100개라면 표준편차가 $1/\sqrt{100} = 0.1$ 인 정규분포에서 가중치를 샘플링함
  • Xavier 초기화 (활성화 함수로 sigmoid, tanh 등 사용 시 효과적)
• Batch Normalization
  • 각 레이어에서 출력값의 분포가 너무 한쪽으로 치우치거나 폭발하지 않도록 정규화해 학습 속도를 높이고 안정성을 유지하기 위해 사용
  • 활성화 함수 전 또는 후에 배치되어 출력값의 평균을 0으로, 분산을 1로 정규화
  • 정규화된 값에 $\gamma$(스케일링)와 $\beta$(시프트)를 곱하고 더해 학습 가능한 형태로 만들어 줌
  • 활성화 함수에서 기울기 소실을 방지해주고 모델의 수렴이 더욱 빨라짐