KPMG Future Academy AI 활용 데이터 분석가 3기 31일차 수업을 2024년 12월 31일에 참석했다.
일주일간 파이썬 넘파이와 판다스를 배우기로 하였다.
- 데이터 분석
1.1. NumPy
1. 데이터 분석
1.1. NumPy
Numerical Python
고성능 과학 계산과 고차원 배열에 필요한 수학 패키지
빠른 수치 계산을 위해 c언어로 만들어짐
벡터, 행렬 연산에 편리한 기능 제공
리스트의 장점과 한계
리스트를 통해 다른 타입의 데이터도 한꺼번에 저장 가능하고 요소 변경, 추가 제거 용이.
값의 집합 개념을 넘어선 수학적 계산이 가능해야함
대량의 데이터 처리 속도가 빨라야함
리스트는 각 값의 주소값을 저장
NumPy는 값을 메모리에 직접 저장
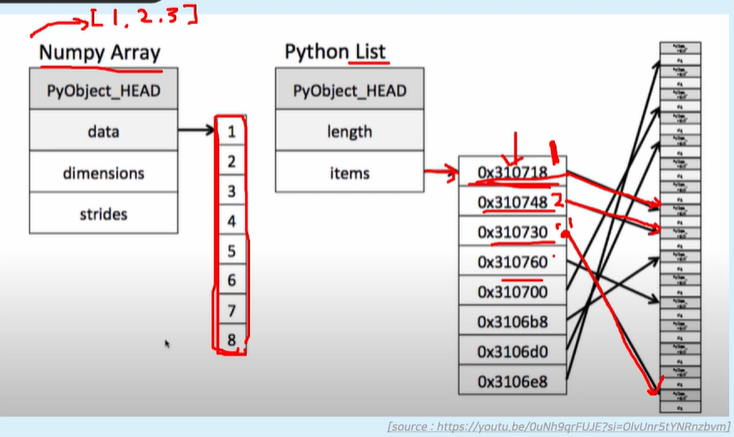
shape 메소드로 축을 출력해볼 수 있음.
NumPy User Guide
https://numpy.org/doc/stable/user/index.html
Open folder하여 파일 불러온 후, 예전에 만들어둔 커널을 미니콘다 가상환경(이름 Streamlit)으로 설정.
activate 가상환경이름
파일 상대경로 복사
변수에 이미지 저장
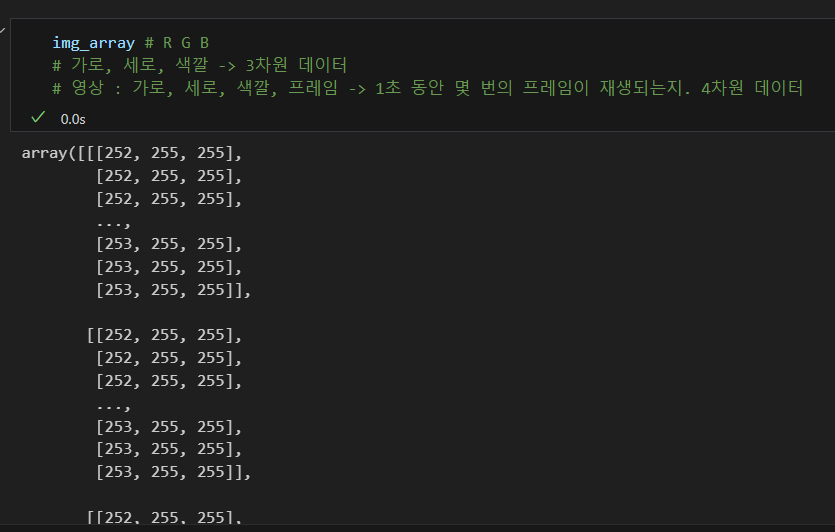
배열로 저장
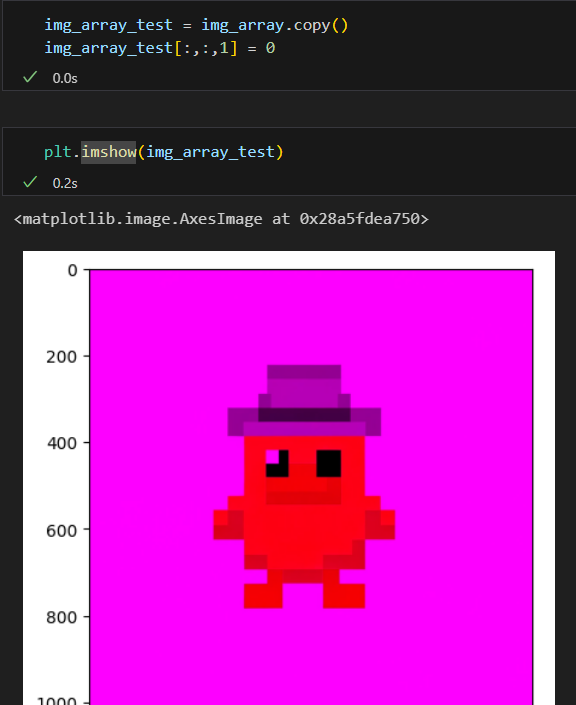
색상 변경 (G 제거) 0,1,2 R,G,B
색상 밝기 변경
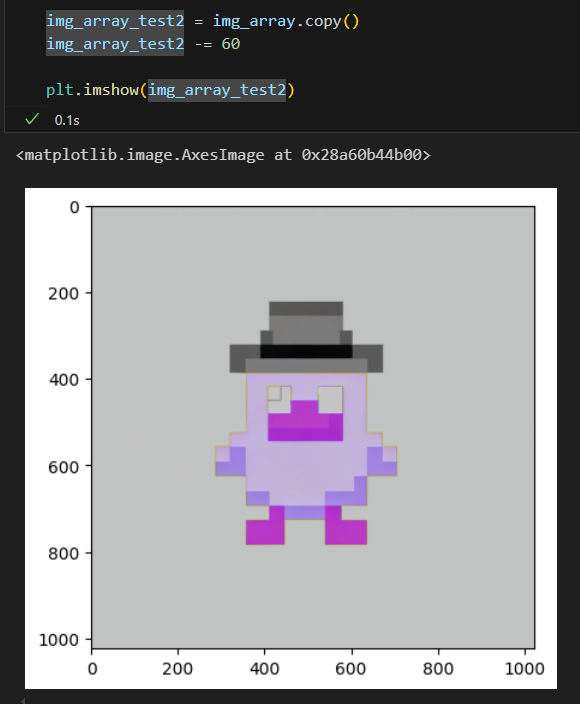
크롭
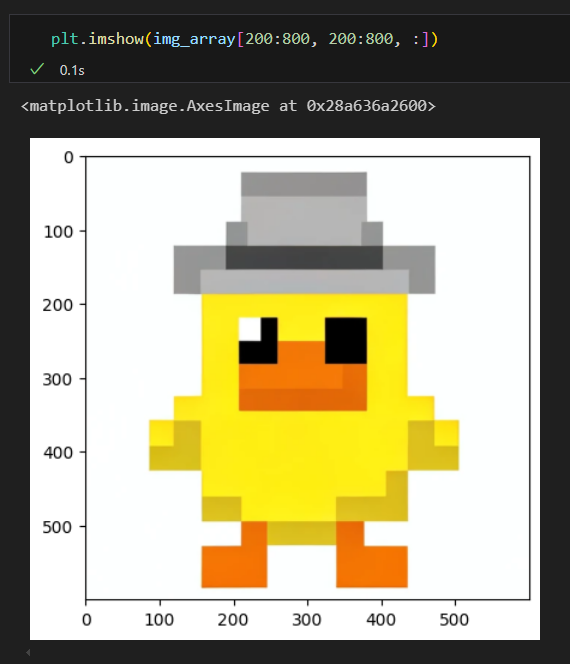
수치 확인
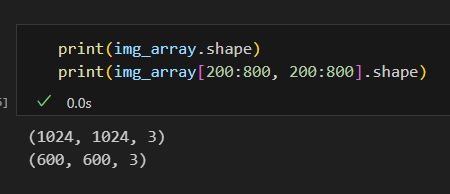
왜 배열을 쓰나?
리스트 값에 연산 적용, 리스트 컴프리헨션

편리하게 요소에 연산 적용
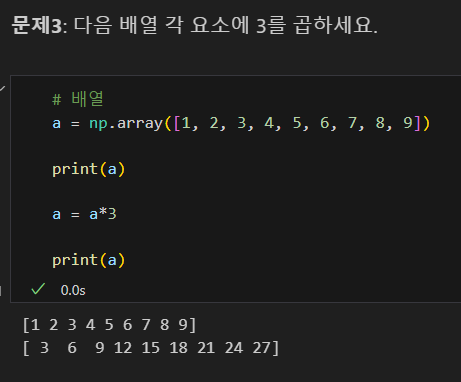
편리하게 짝수 추출
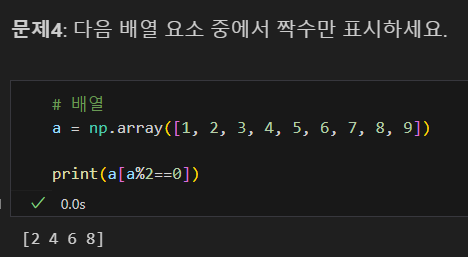
배열


배열 만들기
만들 때는 리스트로 만듦. 머신러닝 결괏값은 배열로 나옴.

1차원 배열 만들기
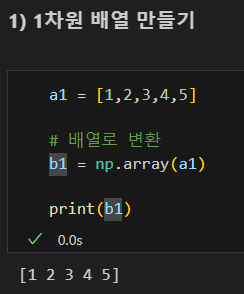
2차원 배열 만들기
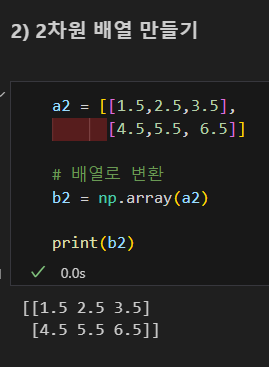
3차원 배열 만들기
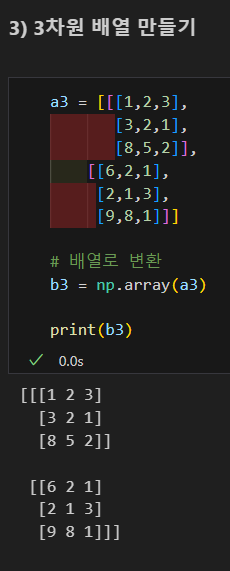
차원 확인하기

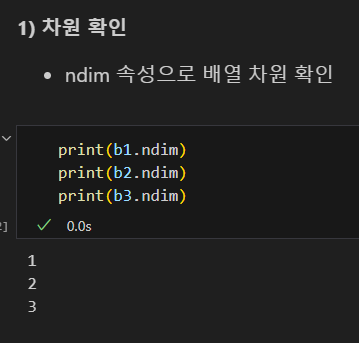
shape 메소드 : 튜플로 형태 확인
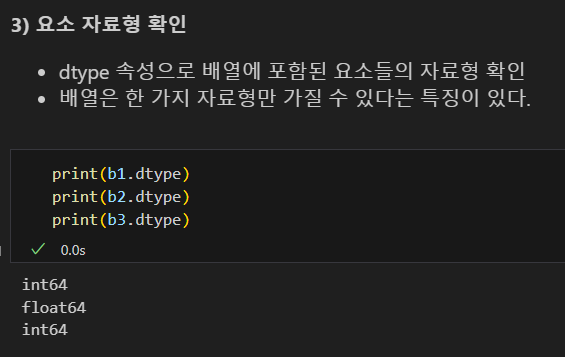
dtype 메소드 : 자료형 확인
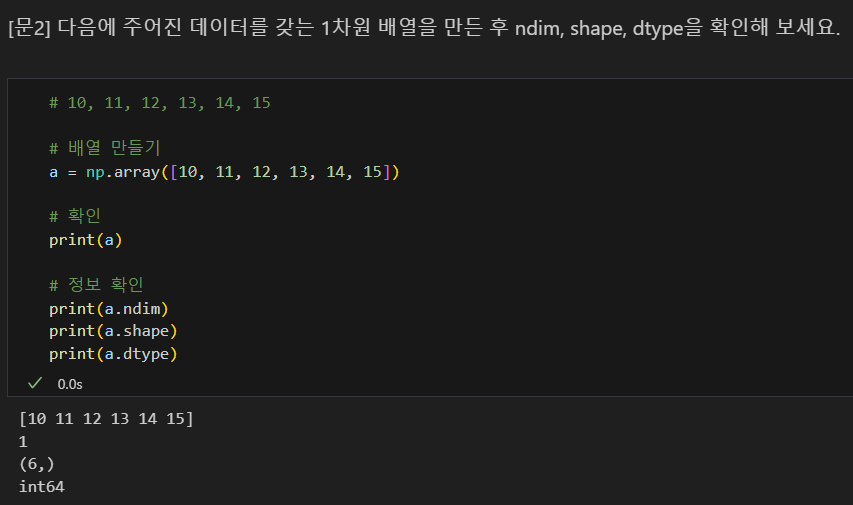
문제
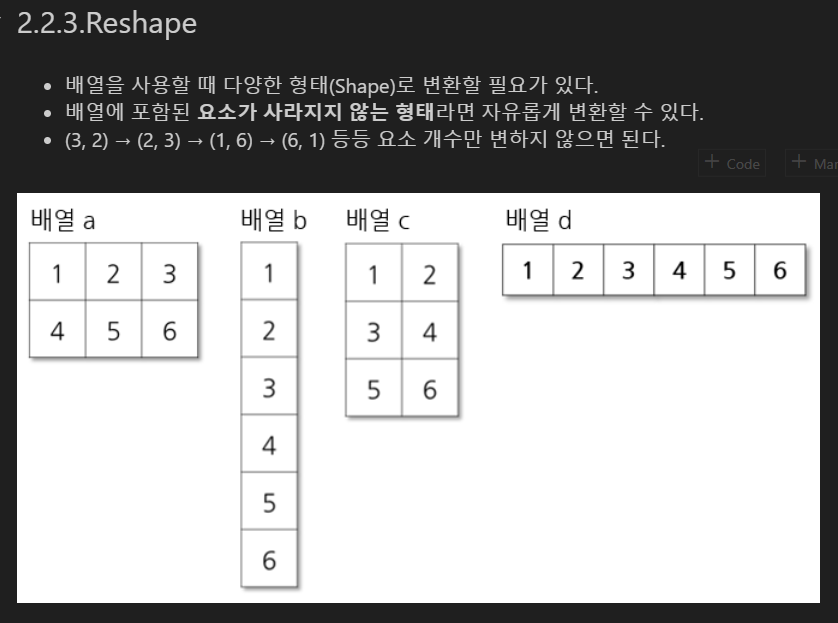
Reshape
numpy 연산에서는 형식이 맞아야하기 때문에 shape 확인 및 변경 필요
reshape 메소드 및 함수를 통해 기존 배열을 새로운 형태의 배열로 다시 구성
배열 요소가 사라지지 않는 형태라면 자유롭게 변환 가능
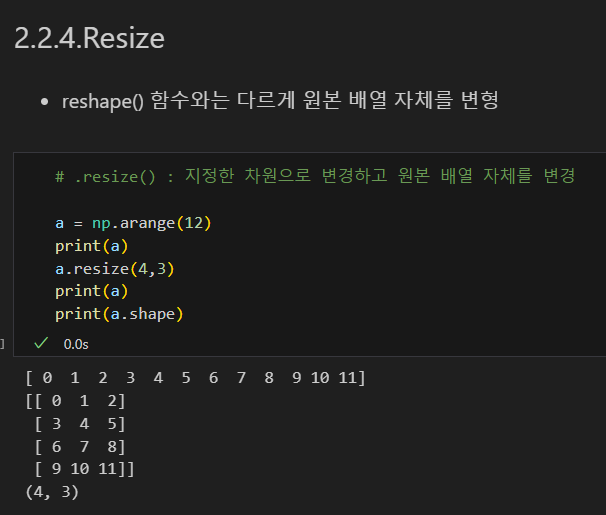
reshape : 새 배열 반환
resize : 기존 배열을 변경
transpose : 행, 열을 교환(arr.T)

2차원 배열 생성
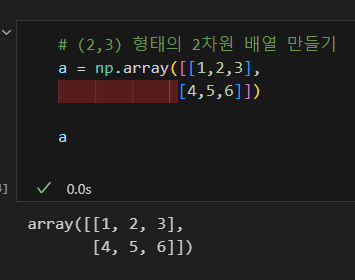
배열 변경
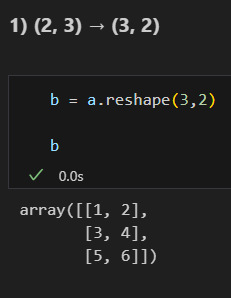
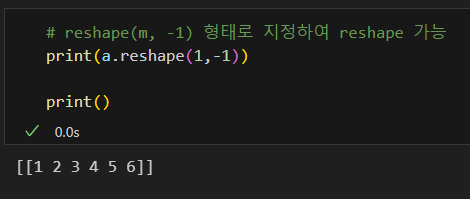
-1의 편리성
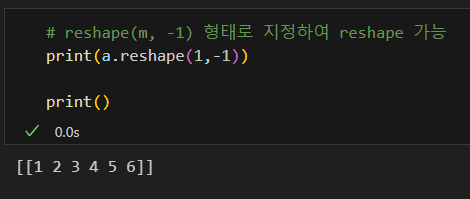
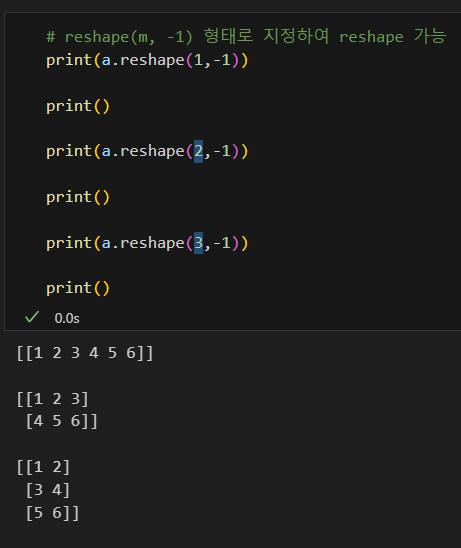
resize는 요소의 갯수가 달라도 0으로 채워서 변경 가능

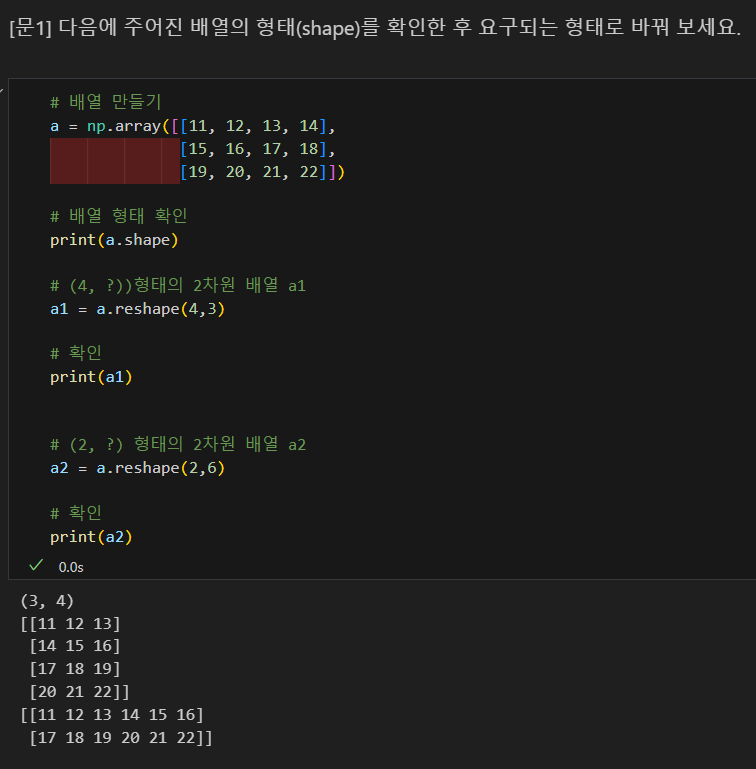
문제
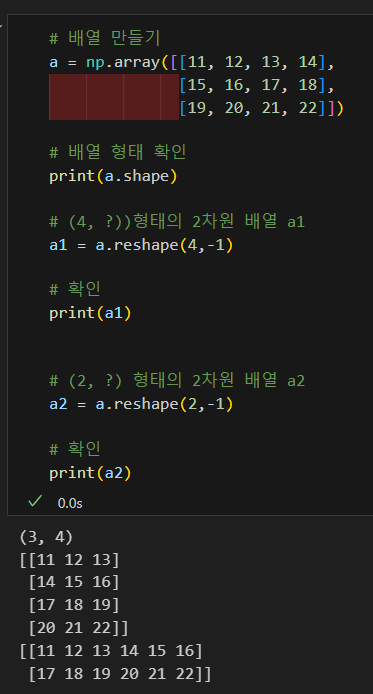
혹은 -1 활용
배열 인덱싱과 슬라이싱

1차원 배열은 리스트와 인덱싱 방법 동일
인덱싱
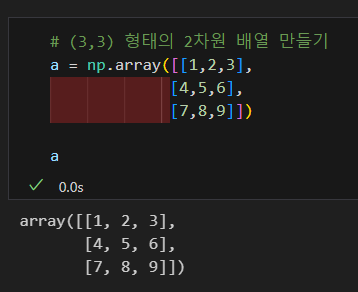
요소 조회
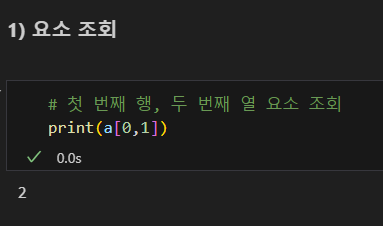
행 조회
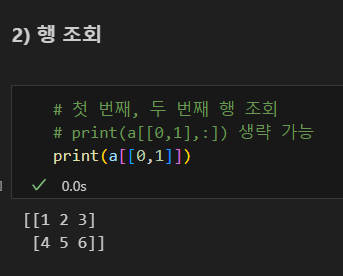
열 조회
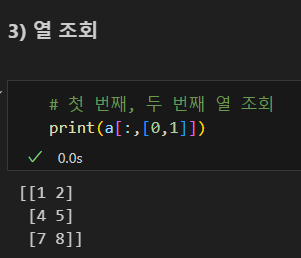
행, 열 조회
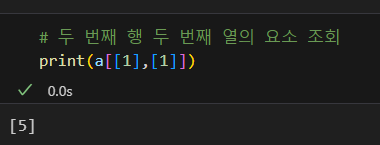
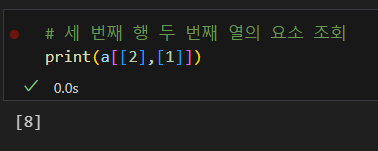
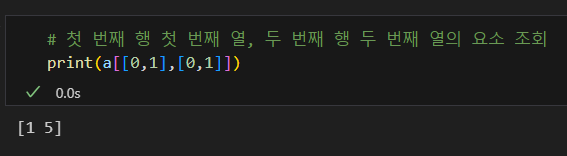

슬라이싱

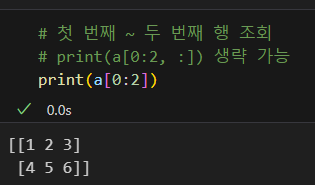
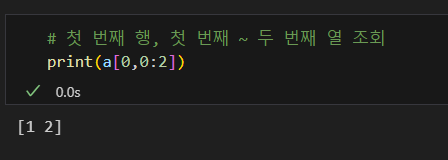
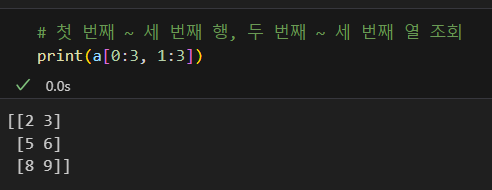
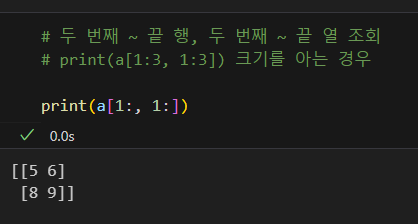
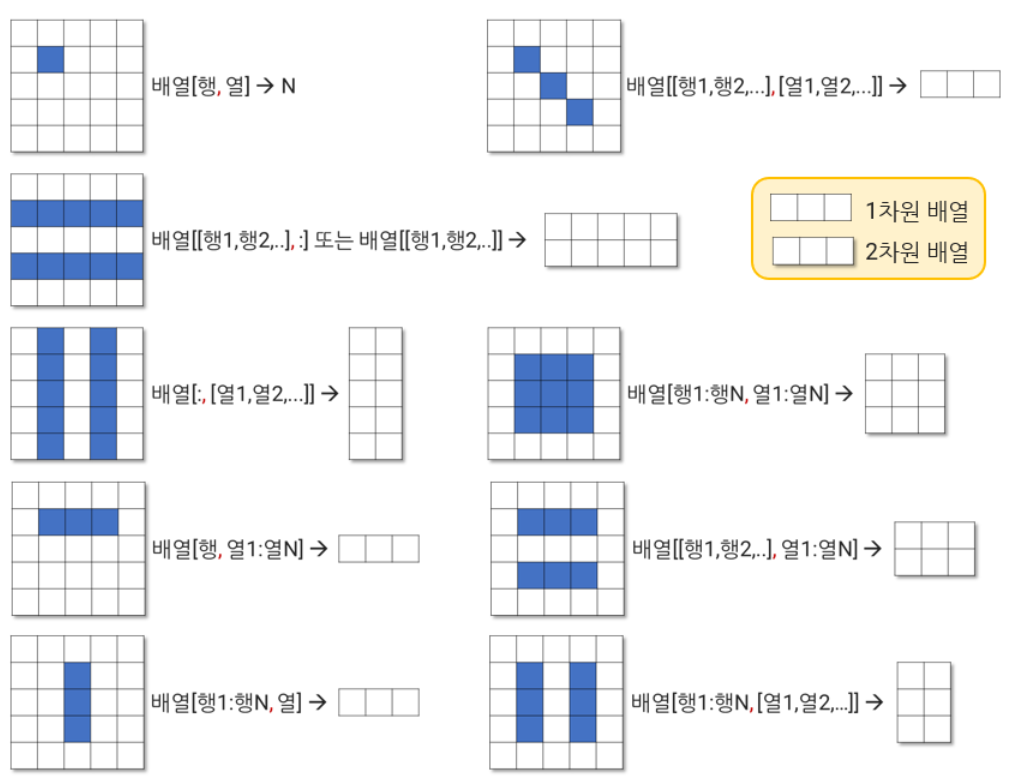
조건 조회
블리안 방식

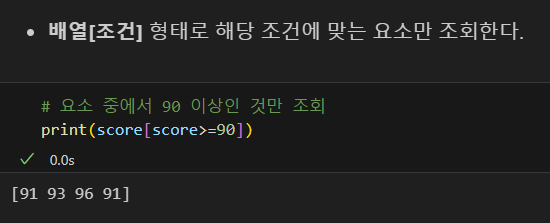
cond 변수로 활용
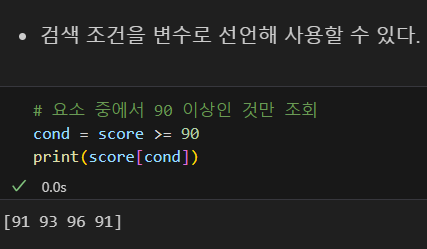
조회 결합 & 연산자 활용
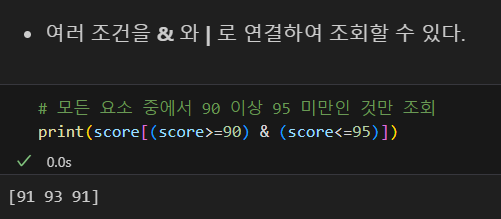
문제
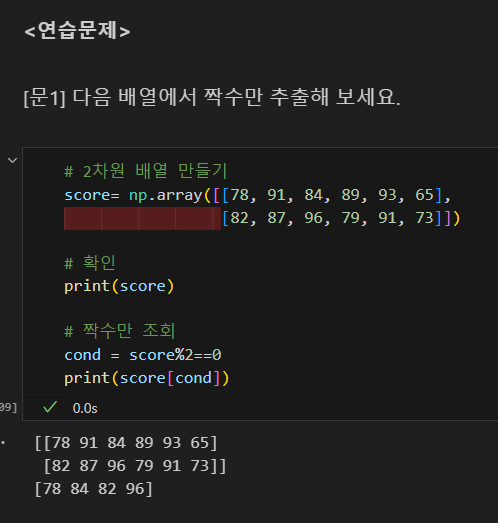
배열 연산
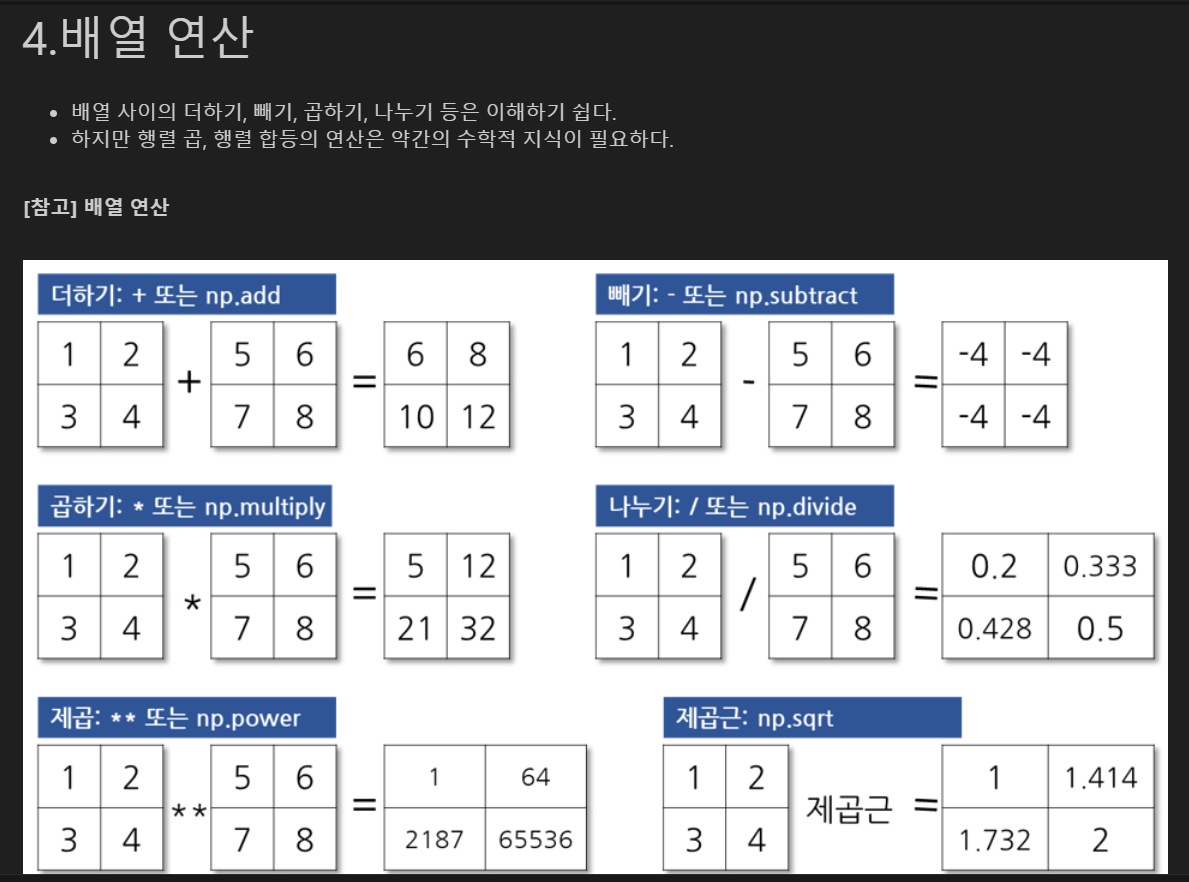
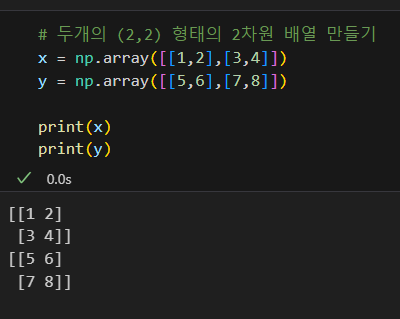
두 개의 2차원 배열 만들기
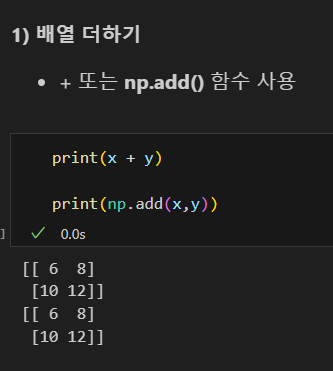
배열 더하기
np.add() 함수
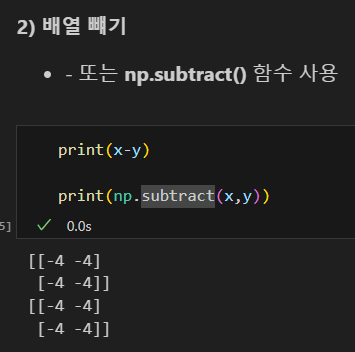
빼기
곱하기
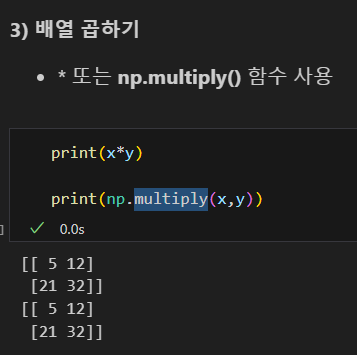
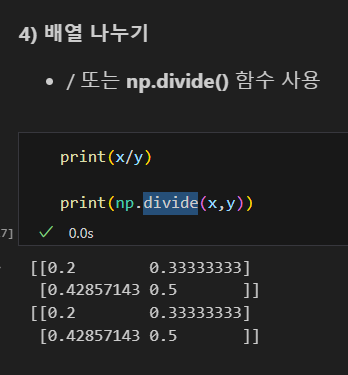
나누기
y 배열 제곱
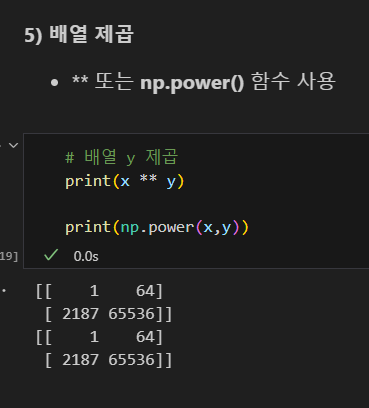
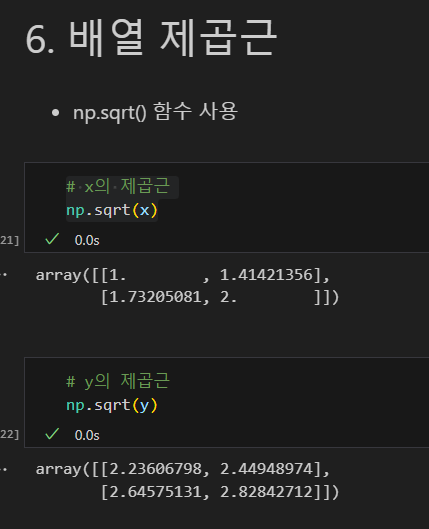
x 배열 제곱
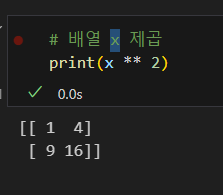
sqrt 합수 사용 제곱근
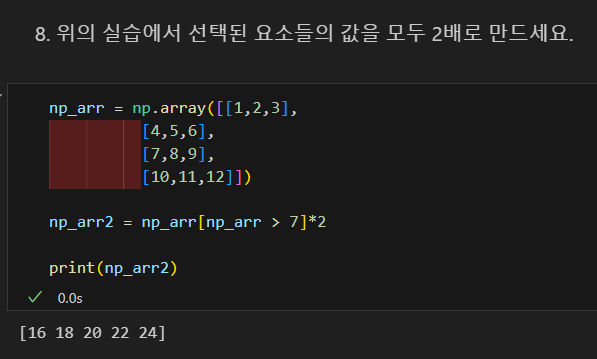
문제 풀기
7보다 큰 숫자만 선택해서 모든 요소에 2 곱하기
번외
이미지 배열 데이터 기초를 배우는 만큼 OCR 등 시중에서 편의를 제공하는 기술에 대해 궁금하여 원리를 알아보았다.

2012 이미지넷
컴퓨터 비전
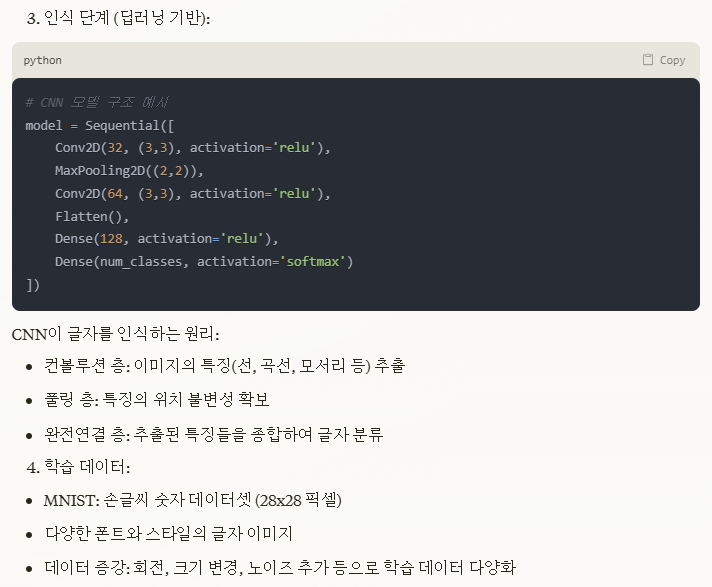
CNN
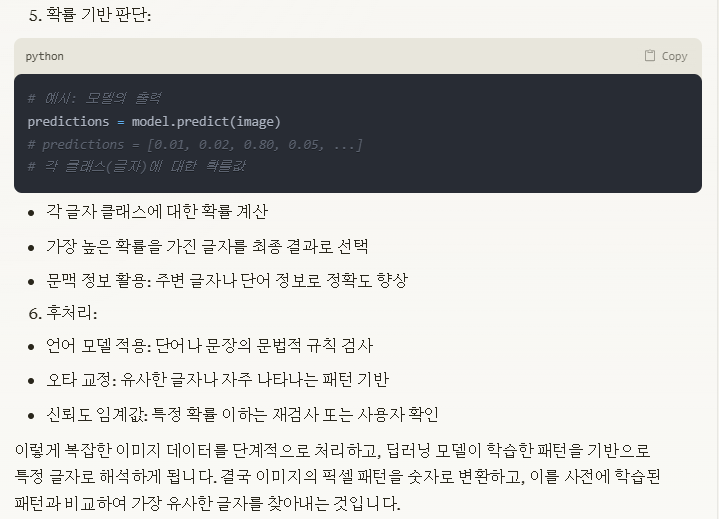
확률 기반 판단
추론 모델
0 - 1사이
신뢰도 임계값
유의성 판단
문맥 포함
번외
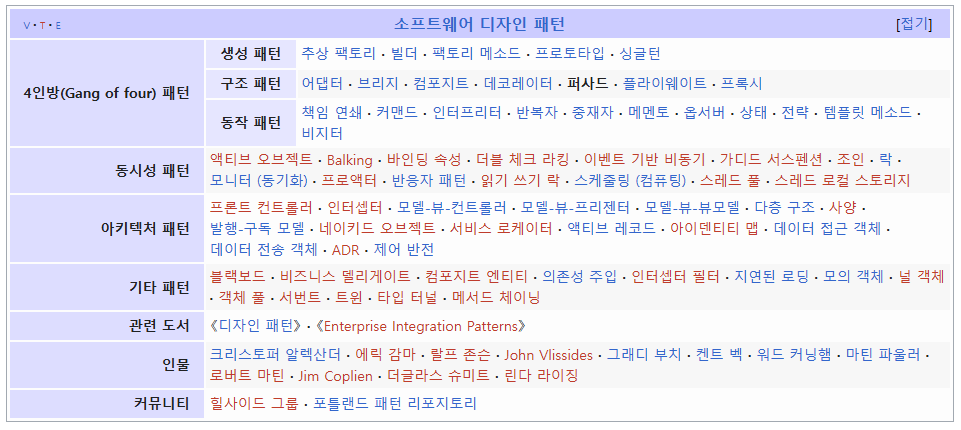
퍼사드 패턴을 검색해보다 알게된 소프트웨어 디자인 패턴
Gang of four는 현업에서 들어본 기억이 있음

예습
PyTorch를 사용하여 자동화된 CNN 모델 구현
https://github.com/Abdul-Rahman-Ibrahim/AutoML-CNN
모델에서
1. 입력 이미지 크기
2. 합성곱 계층
3. 풀링 계층
4. 완전 연결 계층
파라미터를 동적으로 설정 가능
훈련 중 손실 추적과 정확도 평가 기능을 제공
자동화된 훈련 파이프라인을 구축
참고
C++ 컴파일러가 C에서 개선된 점
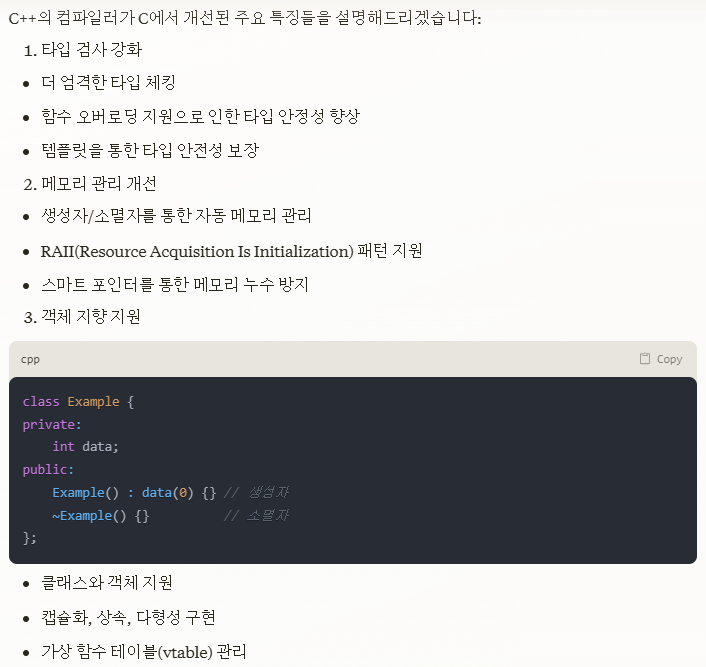
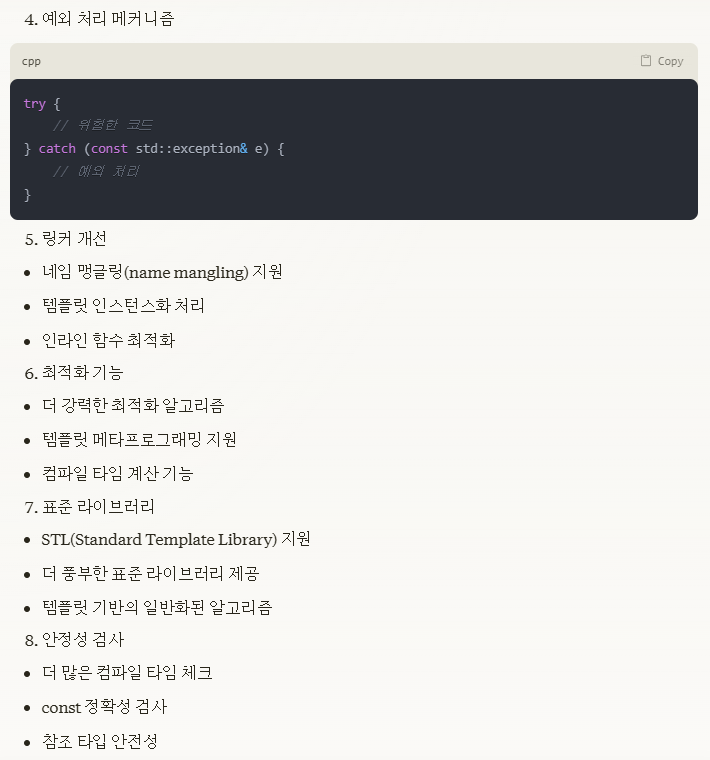
가상 함수 테이블(vtable)
링커에서 네임 맹글링(name mangling) 지원
Torch 컴파일러 관련 참고글
https://chan4im.tistory.com/category/Deep%20Learning%20%3A%20Vision%20System/Pytorch%20%26%20MLOps
ML 기계학습 책 레퍼런스

위 책에서 설명한 선형회귀 (Linear Regression)
https://chan4im.tistory.com/239



기저함수(basis function) 확장
최대 우도 추정 (우도란 가능도를 말함. 영어로 Likelihood)
기저 함수 (또는 바탕함수)
서로 직교하면서 선형적으로 독립적인 함수의 집합
자연계에서 발생하는 모든 신호는 함수들의 조합으로 표현할 수 있다. 특정 함수란 일반적인 선형 다항식 함수가 될 수도 있고, 위상이 다른 삼각함수가 될 수도 있다. 이 경우, 선형 다항식 함수 또는 싸인 코싸인과 같은 조합의 기본이 되는 함수를 기저함수라 부른다.
기저는,
- 벡터공간 내에서 선형독립이고, 전체 벡터공간을 생성(span)할 수 있는 원소로 이루어진 집합.
- 가장 적은 수의 선형독립인 벡터들로 이루어진 집합
- 기저 벡터의 수가 벡터 부분공간에서의 차원(dimension)이 됨
기저 벡터는,
- 벡터공간에서 각각의 축방향을 가리키는 단위 벡터
기저 함수는,
- 함수공간의 기저 요소를 이루는 함수
출처 : https://blog.naver.com/0120huny/90116427230
행렬 곱셈의 특별한 규칙
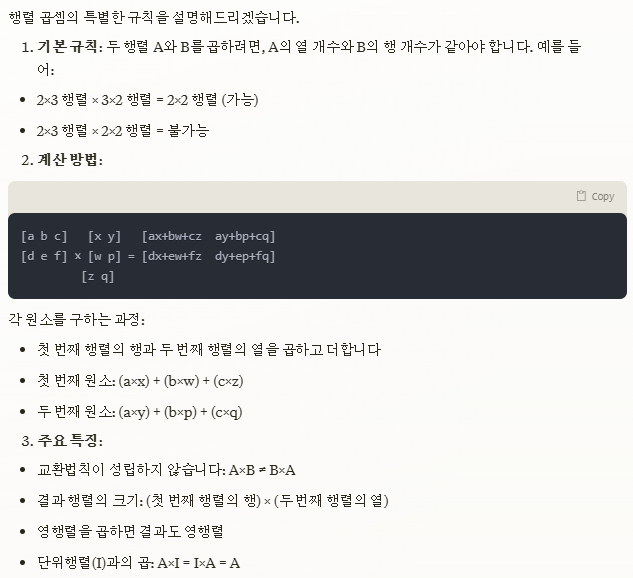
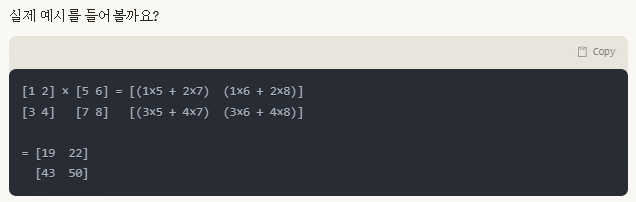
행렬곱(matrix multiplication)과 합성곱(convolution)의 관계



데이터 사이언스를 위한 기초 지식
확률, 통계
[기본 개념]
이산형 변수: 특정 범위 내에서 특정 값만 취할 수 있는 변수
연속형 변수 : 특정 범위 내에서 무한히 많은 값을 취할 수 있는 변수
도수분포표 (frequency table)
*정성적 데이터를 상호배타적(mutually exclusive)이고, 전체포괄(collectively exhaustive)인 계급으로 분류한 후 각 계급에 존재하는 관측치의 도수를 나타낸 표
Class(계급) : 분류 카테고리
Frequency(도수) : 각 계급의 원소 개수
제표(Tabulation): 각 범주에 속하는 빈도수를 구분하여 보여주는 표
단순제표(도수표) : 범주가 한가지 기준으로 나뉘어진 경우
교차제표(분할표) : 범주가 두개이상 기준으로 나뉘어진 경우
*상대도수분포표(Relative frequency distribution)
각 계급에 변수가 존재할 확률(백분율) = 계급 빈도 / 빈도합계
*누적도수분포표(Cumulative frequency distribution)
특정 계급 이하까지의 데이터 빈도(특정 계급 이하 빈도를 모두 더함)
독립성과 상관성:
상관계수(correlation coefficient) : 값의 범위가 -1에서 +1 사이에 속함
*독립성 검정(Test of Independence)
변수가 범주형인 경우 카이제곱 검정을 사용.
변수가 연속형인 경우 공분산을 사용.
카이제곱 검정(Chi-Square Test) : 카이제곱 분포에 기초하여 관찰된 빈도와 기대되는 빈도가 의미있게 다른지 여부 검증.
적합도 검정(Goodness-of-Fit Test) : 하나의 범주형 변수가 특정 분포를 따르는지를 검정.
독립성 검정(Test of Independence) : 두 개 이상의 범주형 변수가 상호 독립적인지 검정.
귀무가설(H0) : A, B는 서로 관계가 없다. 독립이다.
대립가설(H1) : A, B는 서로 관계가 있다. 독립이 아니다.
상관 관계에 대해서 편향을 갖지 않도록 표본을 랜덤 추출할 수 있음.

피어슨의 카이제곱 검정(Pearson's Chi-squared Test) : 표본의 크기가 큰 경우에 사용.
피셔의 정확한 검정(Fisher's Exact Test) : 표본수가 적거나 표본의 교차표를 보았을 때, 특정 셀에 치우치게 분포되어 있을 경우
공분산(convariance)
: 두 확률변수가 얼마나 함께 변화하는지 측정
: 한 변수가 커지거나 작아질 때 다른 변수가 동일하게 커지거나 작아지면 공분산은 양의 값을 가짐. 반대의 경우 음의 값을 가짐.
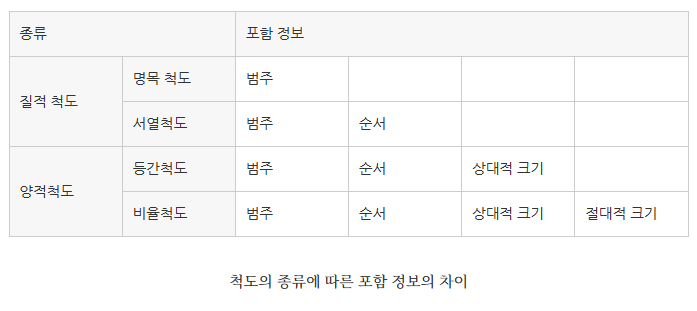
자료의 척도: 명목척도, 서열척도, 등간척도, 비율척도
변수가 질적인 경우 범주형 척도
변수가 양적인 경우 연속형 척도
명목-서열-등간-비율 (데이터의 양이 커짐)
질적 척도
1. 명목 척도(nominal scale) : 성별, 혈액형 등
2. 서열 척도(ordinal scale) : 석차, FIFA 순위 등
양적 척도
1. 등간 척도(interval scale) : 온도, IQ 등
2. 비율 척도(ratio scale) : 몸무게, 매출액 등 (절대적 영점 존재)
[확률 분포와 벡터]
확률변수벡터 x∈R^D
: 다변수 통계, 기계학습, 패턴인식에 사용
스칼라(0차원), 텐서(2차원 이상, 다차원), 벡터(물리에서 1차원. 물리에서 크기와 방향. 데이터 상에서 방향)
-
확률변수벡터(Random Vector)
x는 여러 개의 확률변수들로 구성된 벡터
x = [x₁, x₂, ..., xD]ᵀ 형태로 표현
각각의 xi는 하나의 확률변수 -
∈R^D의 의미
R^D는 D차원 실수 공간을 의미
벡터 x의 각 원소는 실수값을 가질 수 있음
예를 들어 D=3인 경우, x∈R³은 3차원 실수 공간의 점을 나타냄 -
실제 예시
2차원의 경우(D=2): x = [x₁, x₂]ᵀ
예: 키와 몸무게를 나타내는 확률변수 벡터
3차원의 경우(D=3): x = [x₁, x₂, x₃]ᵀ
예: 3차원 공간에서의 위치 좌표를 나타내는 확률변수 벡터
예시 : NumPy 라이브러리를 사용하여 D차원 실수 공간에서 다변량 정규 분포(Multivariate Normal Distribution)를 따르는 랜덤 벡터를 생성
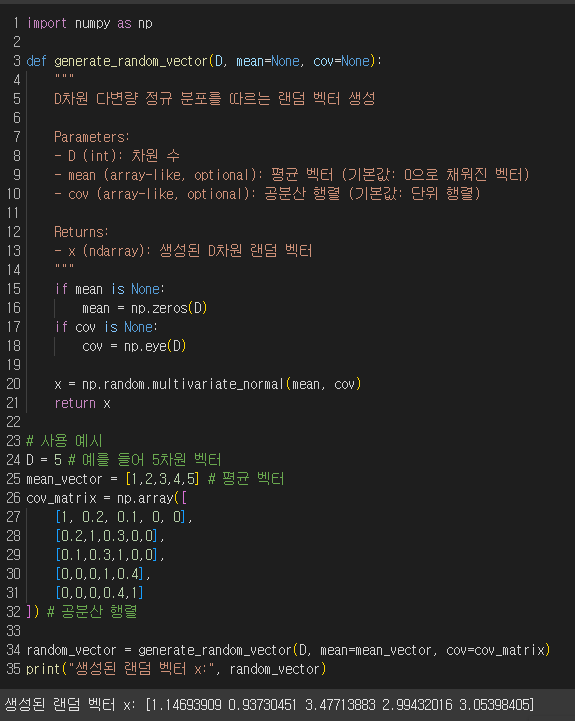
평균벡터 μ∈R^D
공분산행렬 Σ∈R^(D×D)
**정밀도행렬(precision matrix): 공분산행렬의 역행렬 Σ^−1
참고 : 이항분포(표준화) binomial, 포아송 분포, 베르누이 분포
이항분포 : n 번 시행했을때, 원하는 결과(H)가 k번 나올 확률 분포.
확률변수 X가 이항분포 B(n, p)를 따르고 n이 충분히 클때, 정규분포 N(np, npq)를 따른다.
np ≤ 5, nq ≤ 5일때, n이 충분히 크다고 한다.
정규화 종류

[다변수 분포 관련]
다변수정규분포 : TBD
확률밀도함수 : TBD
평균 벡터 μ와 공분산행렬 Σ의 해당 분할 : TBD
다변량 가우시안 분포 : TBD
마할라노비스 거리 : TBD
기타 다변수 분포: 다항 분포, 디리클레 분포
추정 방법: 최대우도추정(MLE), 베이지안 추정
특성 및 성질: 축척 불변성, 직교성
[검정]
T검정, 아노바 : TBD
유의성 검정 : TBD
p-값과 신뢰구간
다중 비교 보정: 본페로니 보정, FDR
비모수 검정: 윌콕슨 검정, 크루스칼-왈리스 검정
[확률, 분포 추리 통계]
추정 이론: 점 추정, 구간 추정
추정 방법: 최대우도추정(MLE), 최소제곱추정(OLS)
베이지안 추론: 사전 확률, 사후 확률
표본 이론: 중심극한정리, 대수의 법칙
모델 선택 기준: AIC, BIC
---딥러닝 관련---
[행렬 연산]
Jacobian matrix(야코비안행렬)
기본 선형대수: 행렬의 곱, 전치, 역행렬, 특이값 분해(SVD)
텐서 연산: 고차원 배열 다루기
자동 미분: 그래디언트 계산 방법
[컨볼루션]
컨볼루션: Impulse Signal과 Impulse Response로 Output Signal을 구하는 컴퓨팅 기법
컨볼루션 연산: y[n]=k∑x[k]h[n−k]
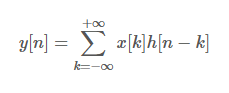
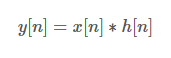
이는 행렬곱 𝐻⋅𝑥와 동등
Toeplitz 행렬로 표현 가능
합성곱 신경망(CNN)의 기본 구조: 컨볼루션 층, 풀링 층, 활성화 함수
고급 컨볼루션 기법: 깊이별 분리 합성곱, dilated convolution
컨볼루션의 응용 분야: 이미지 처리, 시계열 분석
SIFT 알고리즘
최신 딥러닝 기술 동향
최적화 기법: 확률적 경사 하강법(SGD), Adam, RMSprop
정규화 기법: 드롭아웃, 배치 정규화
신경망 구조: 순환 신경망(RNN), 장단기 기억 네트워크(LSTM), 트랜스포머(Transformer)
주의 메커니즘: 어텐션 메커니즘, 셀프 어텐션
자기지도 학습(Self-Supervised Learning)
전이 학습(Transfer Learning) 및 미세 조정(Fine-Tuning)
