day 037 KPMG Future Academy

sottuggung·2025년 1월 15일
AIKPMGfutureacademyt검정다변량데이터분석분포중심화아노바검정이변량파이썬피어슨
0

KPMG-future-academy

목록 보기
34/41

KPMG Future Academy AI 활용 데이터 분석가 3기 37일차 수업을 2025년 1월 9일에 참석했다.

  1. 데이터 분석
    1.1. 두개의 범주를 분석
    1.1.1. 이변량 분석 : 숫자 vs. 숫자
    1.1.2. 이변량 분석 : 범주 vs. 숫자
    1.2. 세개 이상의 범주를 분석
    1.2.1. ANOVA 분산 분석

1. 데이터 분석

가설을 통한 검정 과정에서 보이는 것이 전부가 아님을 유의해야함.

x 연속형, 연속형
시각화 : scatter
수치화 : 상관분석

x 연속형, 범주형
시각화 : boxplot, histogram, density plot
수치화 : (NaN)

x 범주형, 범주형
시각화 : barplot
수치화 : 카이 제곱 검정

x 범주형, 연속형
시각화 : 평균 비교, barplot(sns.barplot)
수치화 : T 검정, 분산분석(ANOVA)

1.1. 두개의 범주를 분석

1.1.1. 이변량 분석 : 숫자 vs. 숫자

이변량 분석 : 숫자 vs. 숫자
scatter

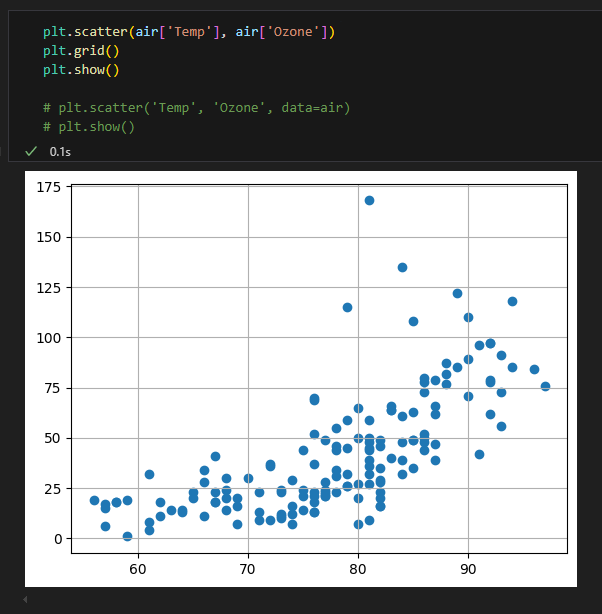
pairplot

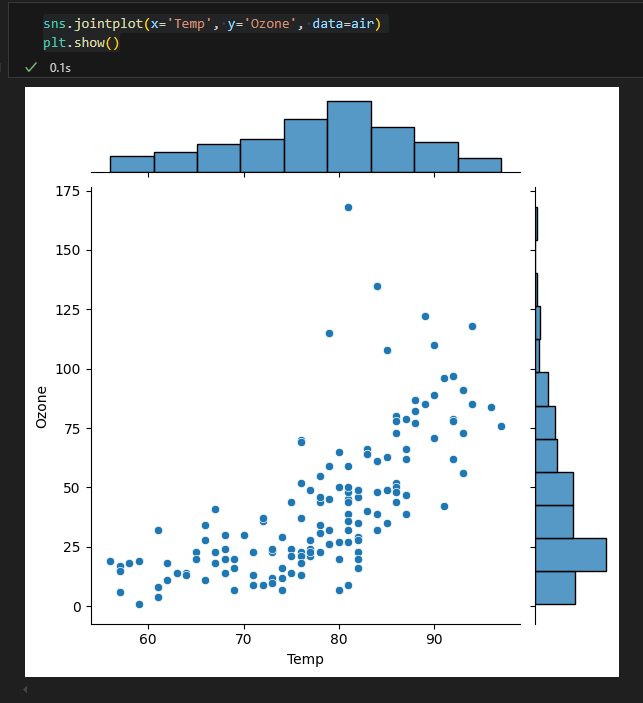
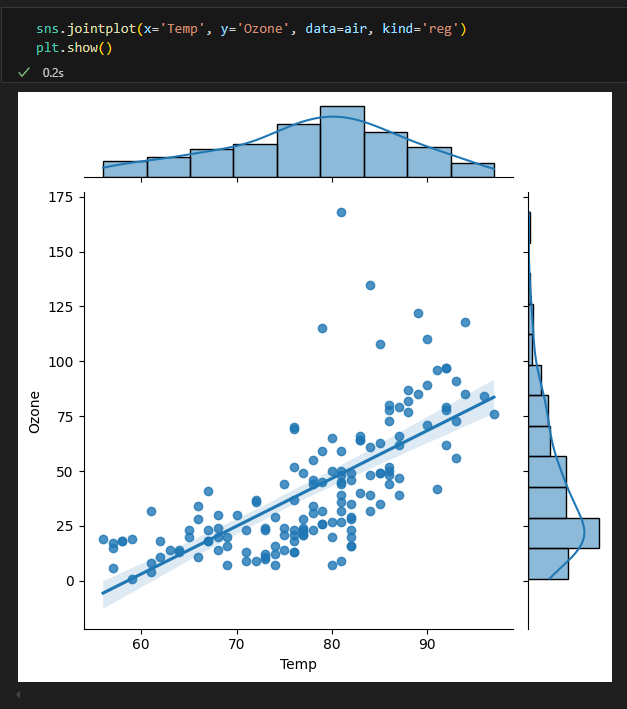
jointplot

범위 크로스(range cross) :
회귀분석에서 상관관계의 방향이 바뀌는 현상.
데이터의 특정 범위에서는 양의 상관관계를 보이다가 다른 범위에서는 음의 상관관계를 보이는 것. 이를 시각적으로 설명하자면:

이러한 현상이 발생하는 주요 원인들은:

비선형관계: 변수들 간의 관계가 단순한 선형이 아닐 때
하위집단 효과: 데이터가 서로 다른 특성을 가진 하위집단들로 구성되어 있을 때
교란변수의 영향: 제3의 변수가 관계에 영향을 미칠 때

이런 경우에는 단순 선형회귀보다는 비선형 회귀나 구간별 분석 등 더 적절한 분석 방법을 고려해야 함. 범위 크로스가 발견되면 데이터의 특성을 더 자세히 살펴보고, 현상의 원인을 파악하는 것이 중요.

상관계수, p-value(유의 확률)

  • 상관계수 𝑟

    • 공분산을 표준화 한 값 (공분산 covariance : 2개의 확률변수의 선형 관계를 나타내는 값)
    • -1 ~ 1 사이의 값
    • -1, 1에 가까울 수록 강한 상관관계를 나타냄.

  • 경험에 의한 대략의 기준(절대적인 기준이 절대 아니다.)

    • 강한 : 0.5 < |𝑟| ≤ 1
    • 중간 : 0.2 < |𝑟| ≤ 0.5
    • 약한 : 0.1 < |𝑟| ≤ 0.2
    • (거의)없음 : |𝑟| ≤ 0.1

분모 : 표준편차를 곱함. 즉 분산의 제곱근

평균과의 차이를 구하는 것은 데이터의 분포를 중심화(centering)하는 과정으로, 상관관계를 더 정확하게 계산하는데 도움이 됨

x̄ (x바)는 x의 평균(mean)

x̄ (x바)는 x의 평균(mean)을 의미한다. 마찬가지로 ȳ (y바)는 y의 평균을 의미함.
이 상관계수(r) 공식:

(x - x̄)는 각 x값에서 x의 평균을 뺀 편차
(y - ȳ)는 각 y값에서 y의 평균을 뺀 편차

예를 들어, x값들이 [2, 4, 6, 8]이라면:

x̄ (x의 평균) = (2 + 4 + 6 + 8) ÷ 4 = 5
(x - x̄)는 각각 [-3, -1, 1, 3]

데이터를 중심화하는 이유 :
1. 공분산 계산의 정확성
원점(0,0)을 기준으로 변수들 간의 관계를 파악할 수 있음
데이터의 실제 패턴과 관계를 더 정확하게 파악할 수 있음

2. 수치적 안정성
매우 큰 값들을 다룰 때 계산 오차를 줄일 수 있음
예를 들어 x값이 모두 1000 이상인 경우, 중심화하면 작은 수들로 계산할 수 있어 정밀도가 높아짐

3. 해석의 용이성
변수들의 스케일에 관계없이 순수한 관계를 볼 수 있음
평균을 0으로 맞추면 변동(variation)을 더 쉽게 해석할 수 있음

간단한 예시:
기온(섭씨) = [25, 26, 27, 28]
아이스크림 판매량 = [100, 110, 120, 130]
이 데이터를 중심화하면:
기온 편차 = [-1.5, -0.5, 0.5, 1.5]
판매량 편차 = [-15, -5, 5, 15]
이렇게 되면 두 변수의 증감 패턴을 더 명확하게 볼 수 있음.

  • p-value (유의확률): 두 변수 간의 상관관계가 우연에 의해 발생했을 확률을 의미함

  • 판단 기준(유의수준)

    • p-value < 0.05: 통계적으로 유의미한 상관관계 -> 상관계수가 의미가 있다.
    • p-value ≥ 0.05: 유의미하지 않음 (즉, 우연에 의한 상관일 가능성이 높음) -> 상관계수가 의미가 없다.

  • 상관계수와 p-value를 한 마디로 정리하자면:

    • 상관계수(r) : 두 변수의 관계 강도 측정
    • p-value : 그 관계가 우연이 아닐 확률 확인

통계 및 확률분포와 관련된 기능 제공하는 모듈

2.1977698002001793e-22 (e-22 = 10^-22)

히트맵

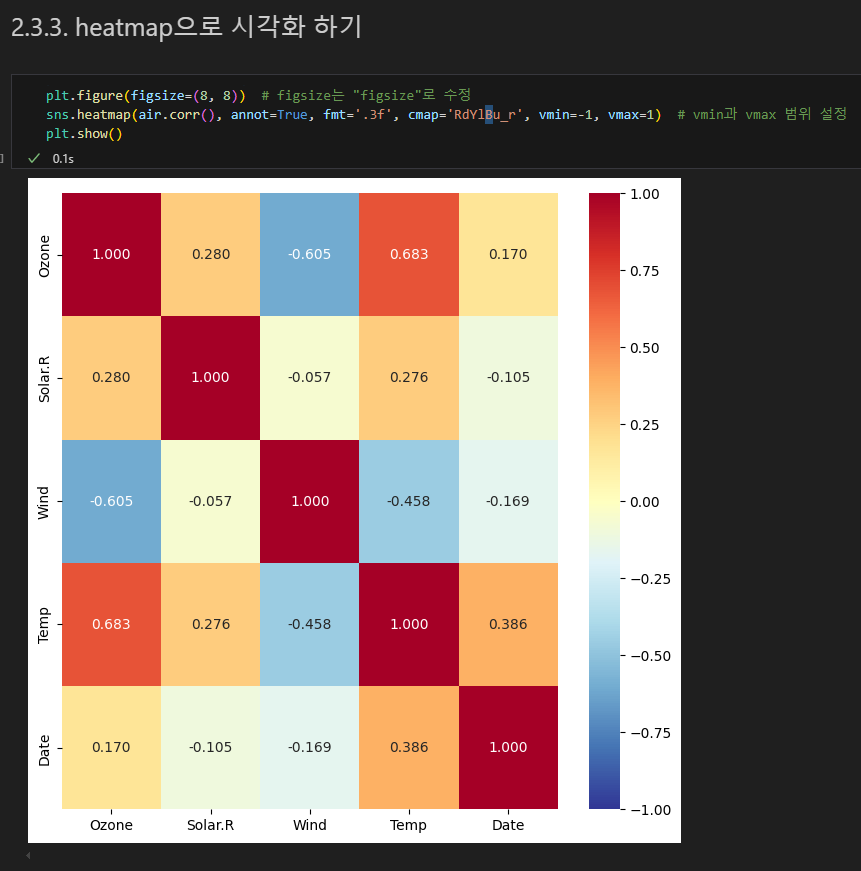
color map 변경 :
cmap(color map) : https://matplotlib.org/stable/tutorials/colors/colormaps.html

  • 상관 계수의 한계
    • 상관계수는 직선의 관계(선형관계)만 수치화 해준다.
    • 직선의 기울기, 비선형 관계는 고려하지 않는다.

오존(Ozone)과 태양복사(Solar.R)의 피어슨 상관계수를 구할 때 한 데이터 열에 결측치가 있어서 전처리가 필요했다. 우선 선형보간법으로 태양복사를 채워서 상관계수를 구해보았다.

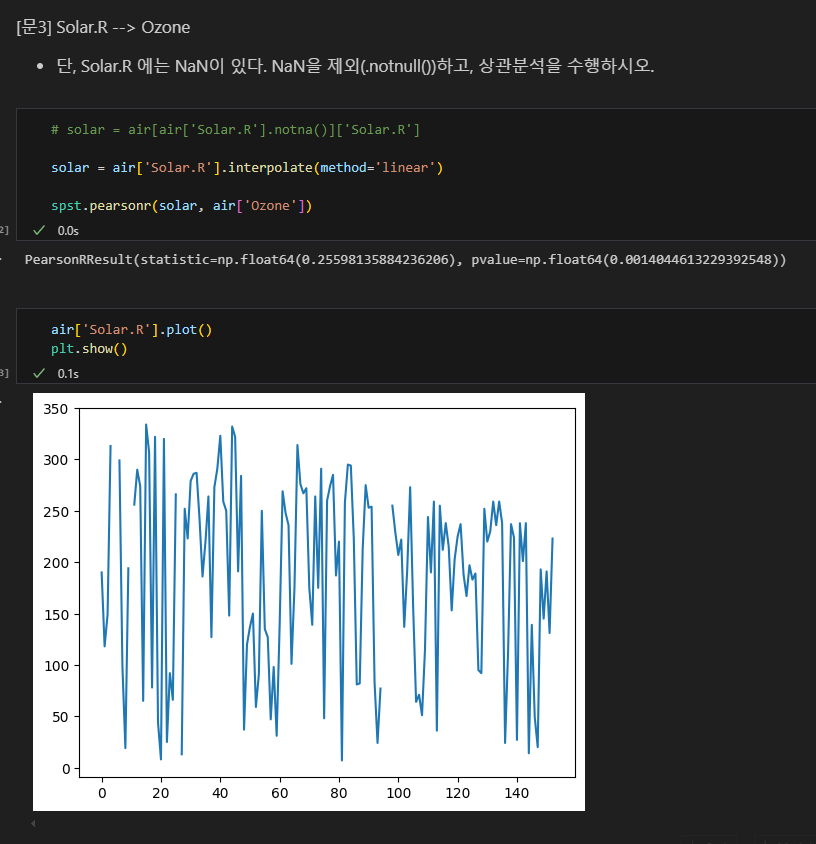
그러나 태양복사는 일관된 선형 데이터가 아니어서 적합하지 않은 방법인 것으로 파악된다.

비선형적인 변화를 가진 데이터의 경우 다항식 보간법, 스플라인 보간법 등을 활용.
여기서 Solar.R은 선형적인 변화임.
그러므로 데이터프레임을 새로 만들 때 아래와 같이 태양복사의 결측치가 있는 오존의 행도 함께 제외했다.

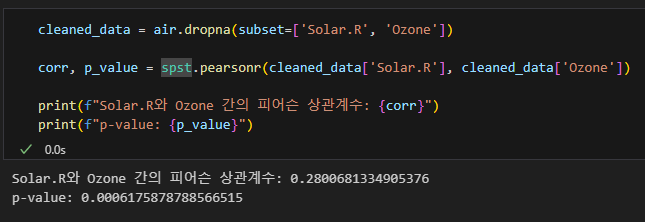
결측치를 채운 것에 비해 더 높은 상관도를 보인다.

지구 자기장과 태양복사의 관계 :

종합 연습문제
보스톤

범죄율과 집값의 상관

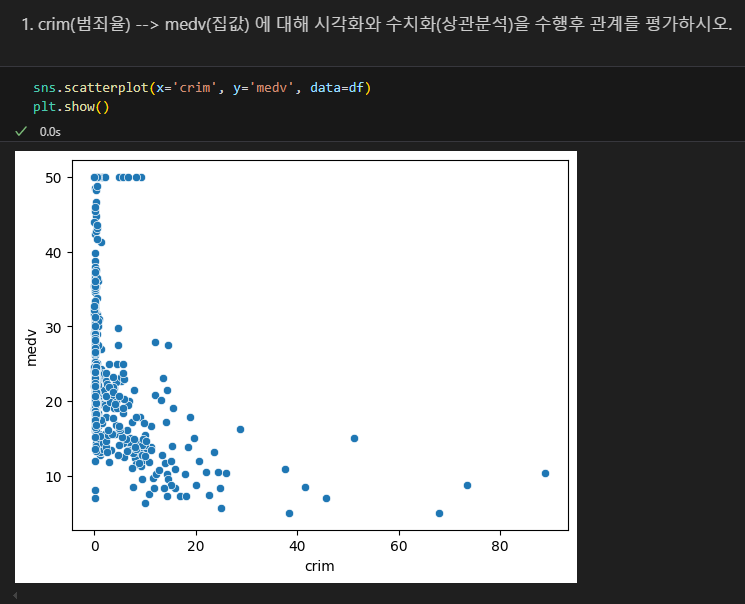
음의 상관관계

함수로 만듦

세금과 집값의 상관

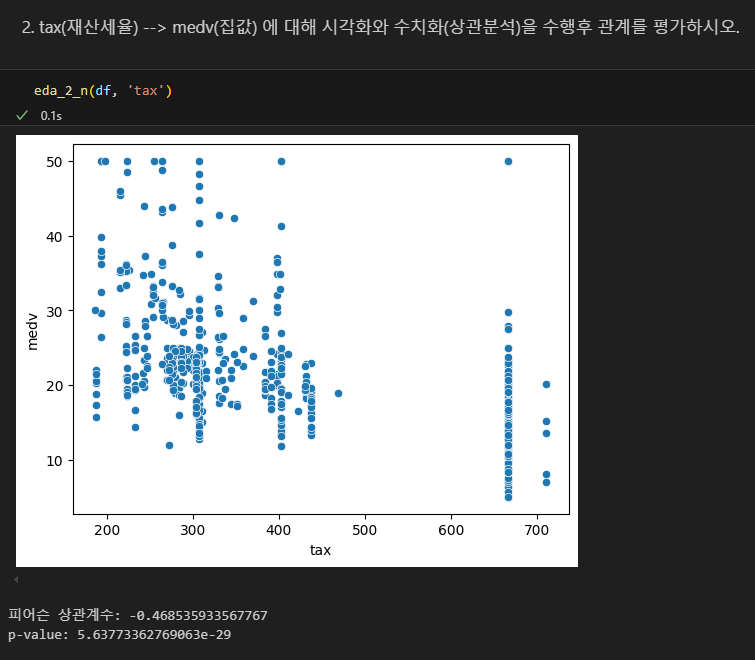
음의 상관관계

하위계층 비율과 집값의 상관

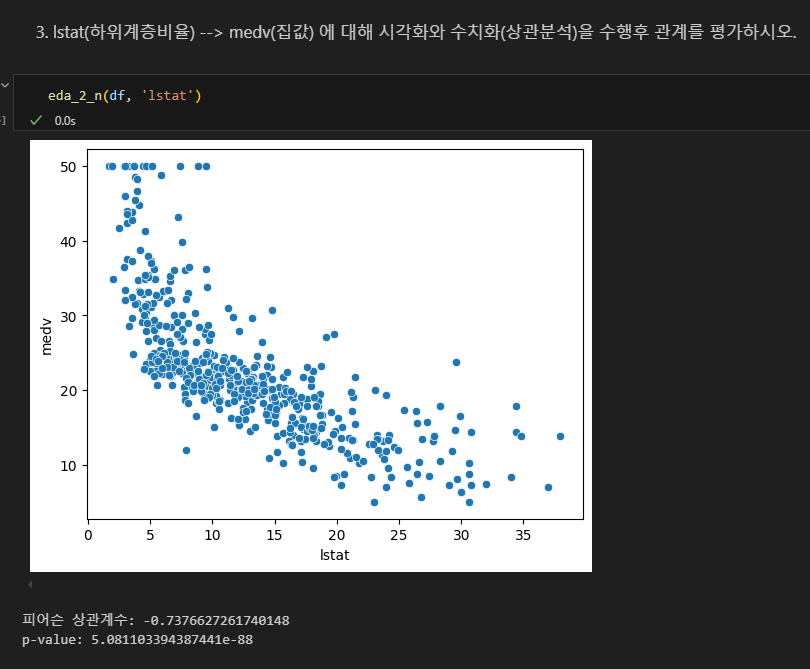
강한 음의 상관관계

교사 1명 당 학생수와 집값의 상관

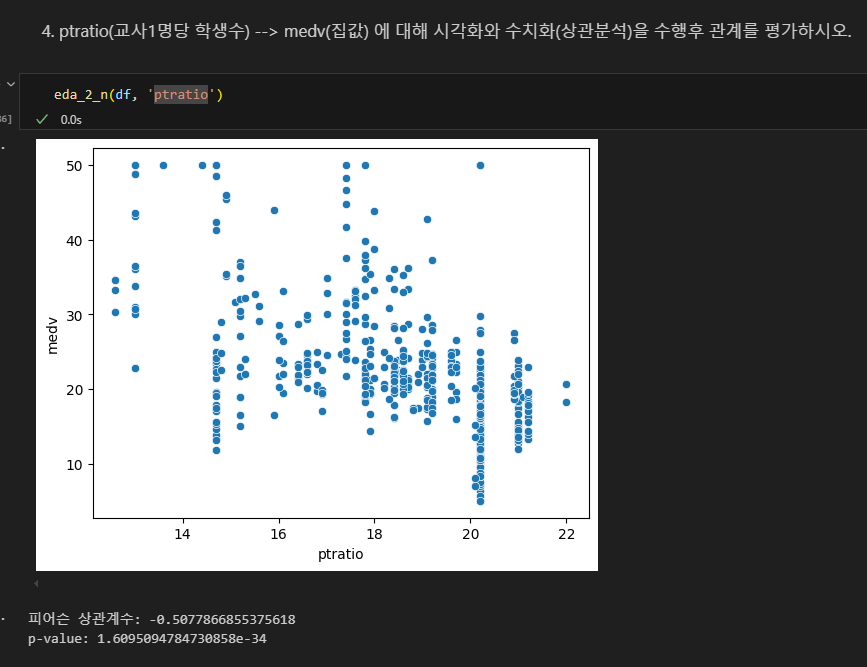
음의 상관관계

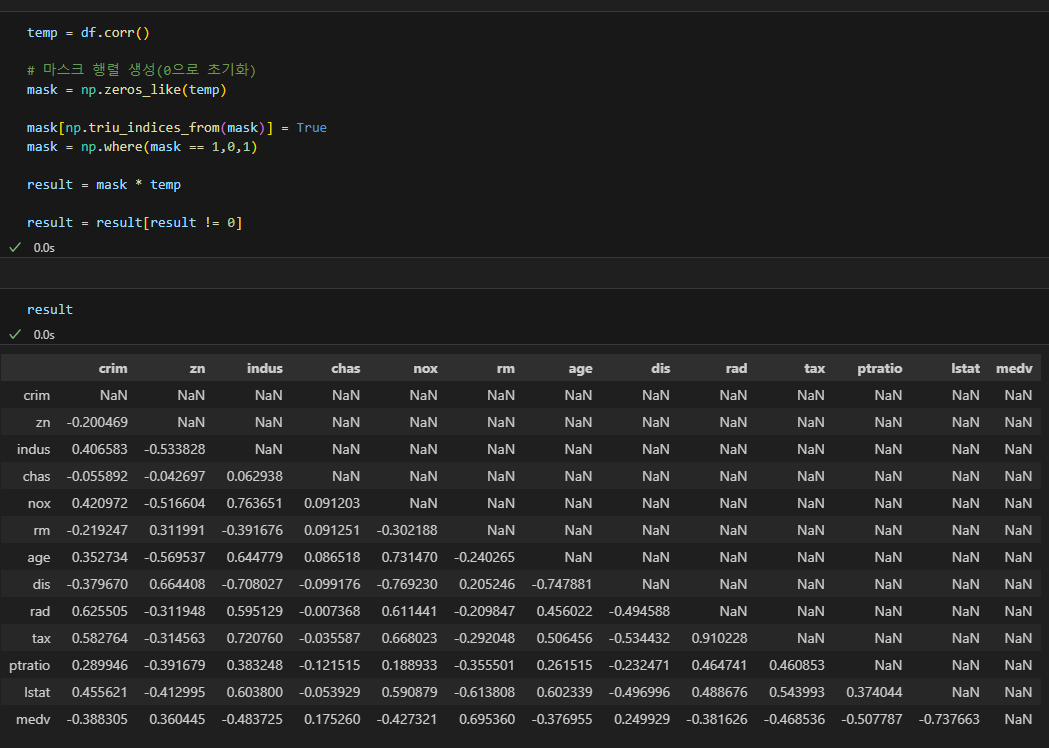
전체 상관도 파악 (히트맵)

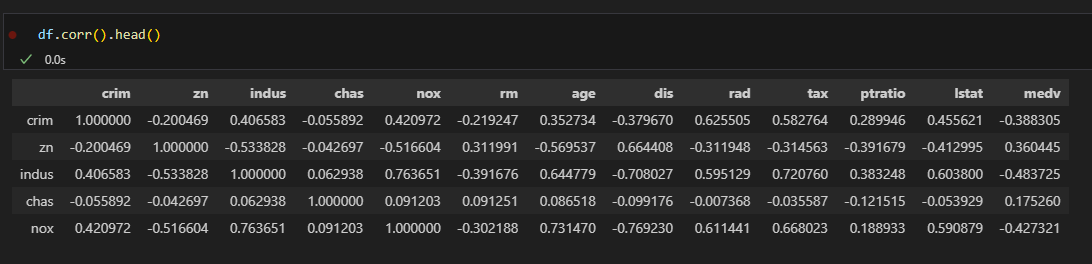
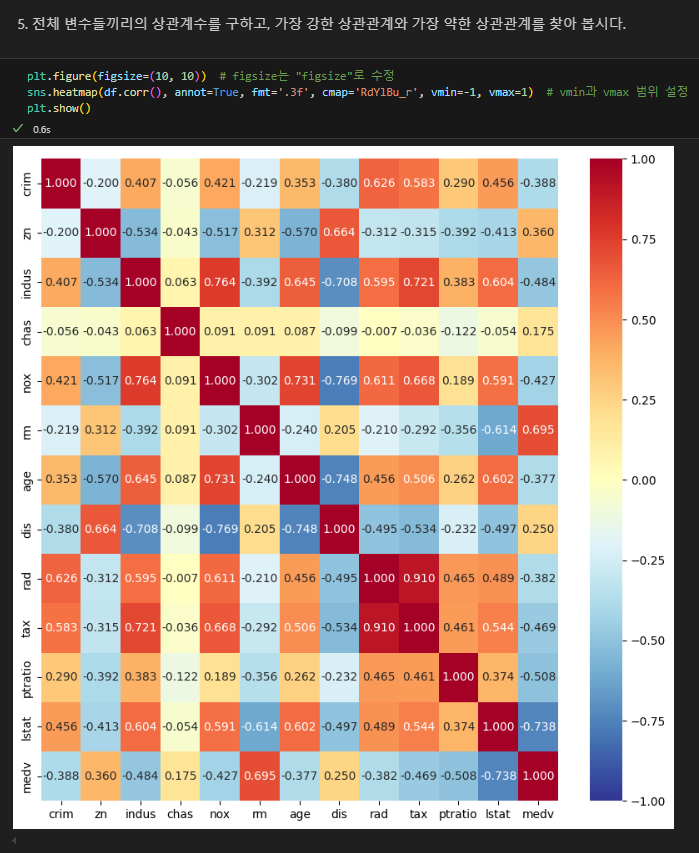
변수설명

  • medv : 1978 보스턴 주택 가격, 506개 타운의 주택 가격 중앙값 (단위 1,000 달러) <== Target
  • crim 범죄율
  • zn 25,000 평방피트를 초과 거주지역 비율
  • indus 비소매상업지역 면적 비율
  • chas 찰스강변 위치(범주 : 강변1, 아니면 0)
  • nox 일산화질소 농도
  • rm 주택당 방 수
  • age 1940년 이전에 건축된 주택의 비율
  • dis 직업센터의 거리 (접근성)
  • rad 방사형 고속도로까지의 거리 (접근성)
  • tax 재산세율
  • ptratio 학생/교사 비율
  • lstat 인구 중 하위 계층 비율

재산세와 고속도로와의 접근성은 강한 양의 상관관계
직업센터 접근성과 일산화질소 농도는 음의 상관관계

추가 분석 : 직업센터 접근성과 일산화질소 농도가 음의 상관관계인 것은 이상하다.

추가로 일산화질소 단변량 분석을 수행.

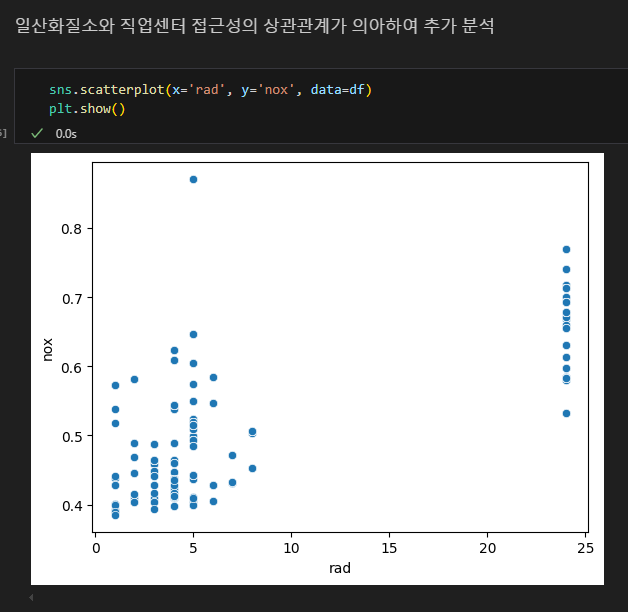
중간에 비어있는 값이 많음.

전처리

통계 관련 책 추천
[교양 서적]

  • 실리콘밸리 데이터 과학자가 알려주는 따라 하며 배우는 데이터 과학
  • 데이터과학 입문
  • 빅데이터 시대, 올바른 인사이트를 위한 통계 101×데이터 분석

[전공 서적]

  • R을 이용한 누구나하는 통계분석
  • 데이터 분석과 해석 R통계학
  • 데이터 과학을 위한 통계
  • 일반통계학

1.1.2. 이변량 분석 : 범주 vs. 숫자

신뢰구간이 겹치면 대립가설 상 유의도가 낮음.

신뢰구간 선은 95%의 신뢰수준을 나타냄. 평균값이 신뢰구간 내에 들어갈 확률이 95%.

중앙값의 차이가 클 수록 대립가설이 유의함.

t-test (t 검정)

  • 두 집단의 평균 비교

    • 예제는 Two sample T-test와 양측검정만 다룬다.
    • 우리는 X --> Y의 관계에서 ,두 변수간에 관련이(차이가) 있는지, 없는지를 확인하는 것이 제일 중요하기 때문이다.

  • 주의사항 : 데이터에 NaN이 있으면 계산이 안된다. .notnull() 등으로 NaN을 제외한 데이터를 사용해야 한다.

  • t 통계량(t-statistic)

    • 두 집단의 평균 차이를 표준오차로 나눈 값
    • 기본적으로는 두 평균의 차이로 이해해도 좋다.
    • 우리의 가설(대립가설)은 차이가 있다는 것이므로, t 값이 크던지 작던지 하기를 바란다.
    • 보통, t 값이 -2보다 작거나, 2보다 크면 차이가 있다고 본다.
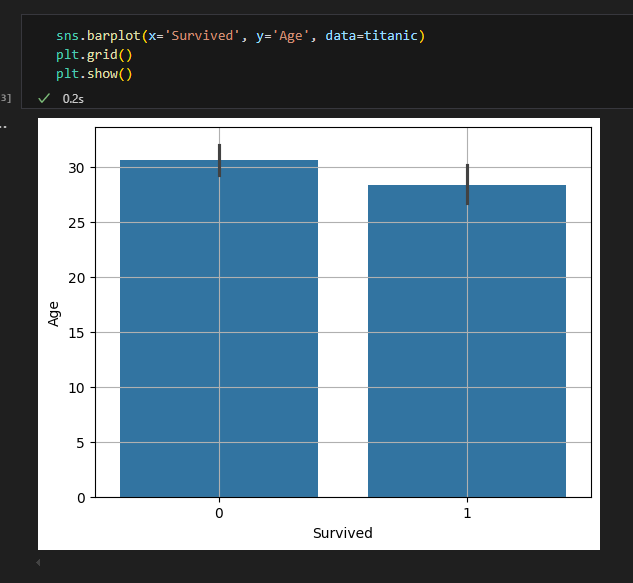
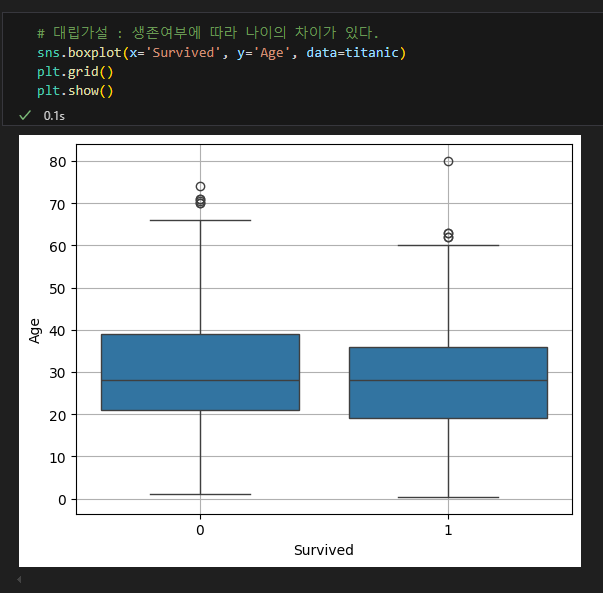
  • 이번엔 타이타닉 데이터로 시도해 봅시다.
    • 생존여부 --> Age : 생존여부 별로 나이에 차이가 있을것이다.

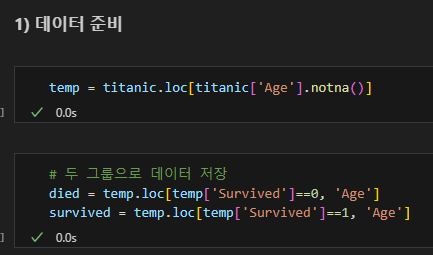
생존자, 비생존자 그룹으로 나누기

  • 귀무가설 : 타이타닉 탑승객 생존 여부별 나이의 차이가 없다.

  • 대립가설 : 생존여부에 따른 나이의 차이가 있다.

  • 기본 문법 : ttest_ind(B,A, equal_var=False)

    • A와 비교할 때 B의 평균이 큰가?
    • equal_var : A와 B의 분산이 같은가?
      • 모르면 False(default)

2.0066이 2와 차이가 있으나 크지는 않다.
p-value : 0.05보다 작으므로 유의미하지만 크게 유의미하지 않다.

연습 1
성별에 따른 운임차이

대립가설 성립. 즉 유의미하게 차이가 있다.

연습 2
생존여부에 따른 운임차이

대립가설 성립. 즉 유의미하게 차이가 있다.

파라미터 : 분포의 형태를 정하는 숫자. 모수.

정규 분포 : 평균과 표준편자 두 개의 파라미터로 된 확률밀도함수를 가짐.

표준화 : z값 도출. 평균과의 거리가 표준편차의 몇 배인가를 나타냄.

추론통계 : 얻은 실현값으로 이 값을 발생시킨 확률분포를 추정한다.
모집단 = 확률 분포
표본 = 확률분포를 따르는 실현값

무작위 추출 : 단순무작위추출법, 층화추출법

표본오차

표본 평균과 모집단 평균 간의 관계 : 큰 수의 법칙 성립. 표본크기가 커질수록 표본평균이 모집단 평균에 가까워짐.

중심극한정리

일치추정량
비편향추정량

표준오차 : 표본오차의 분포는 모집단의 표준편차와 표본크기 등 2개의 값만 정해지면 구할 수 있음.

p값이란 관찰한 값 이상으로 극단적인 값이 나올 확률로 0.02 이하로 적은 경우 귀무가설은 기각된다.

1.2. 세개 이상의 범주를 분석

1.2.1. ANOVA 분산 분석

ALCHERA : 산불 관련 AI 솔루션 도입한 기업

ANOVA

  • 분산 분석 ANalysis Of VAriance
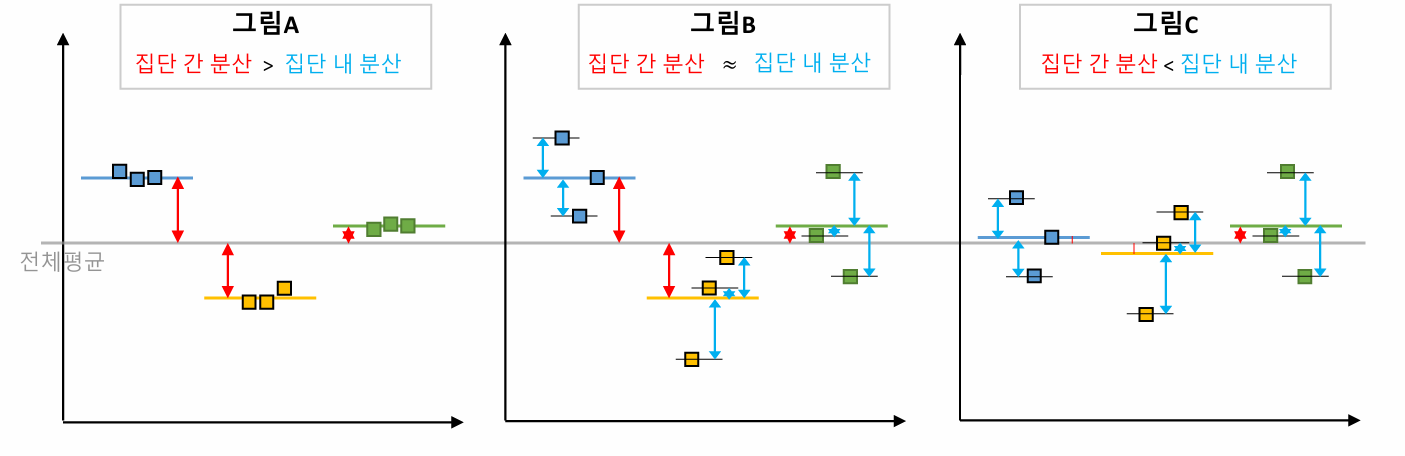
    • ANOVA (Analysis of Variance)는 셋 이상 집단의 평균 차이가 통계적으로 유의미한지를 검정하는 방법
    • 여러 집단 간에 차이는 어떻게 비교할 수 있을까?
    • 여기서 기준은 전체 평균 이다.

  • f분포
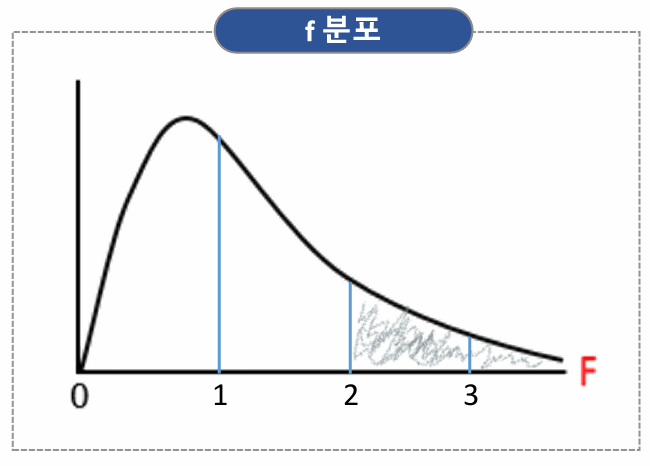
    • 두 개의 독립된 정규분포를 따르는 모집단의 분산 비율로 만들어지는 확률 분포
    • 오른쪽으로 길게 늘어진 비대칭 분포를 가지며, 0에서 시작해서 무한대로 이어짐
    • 값이 대략 2~3 이상이면 차이가 있다고 판단한다.

Pclass의 3개 범주에 따라 Age에 차이가 있을 것이다 가설 검정

신뢰구간 겹치는지 확인

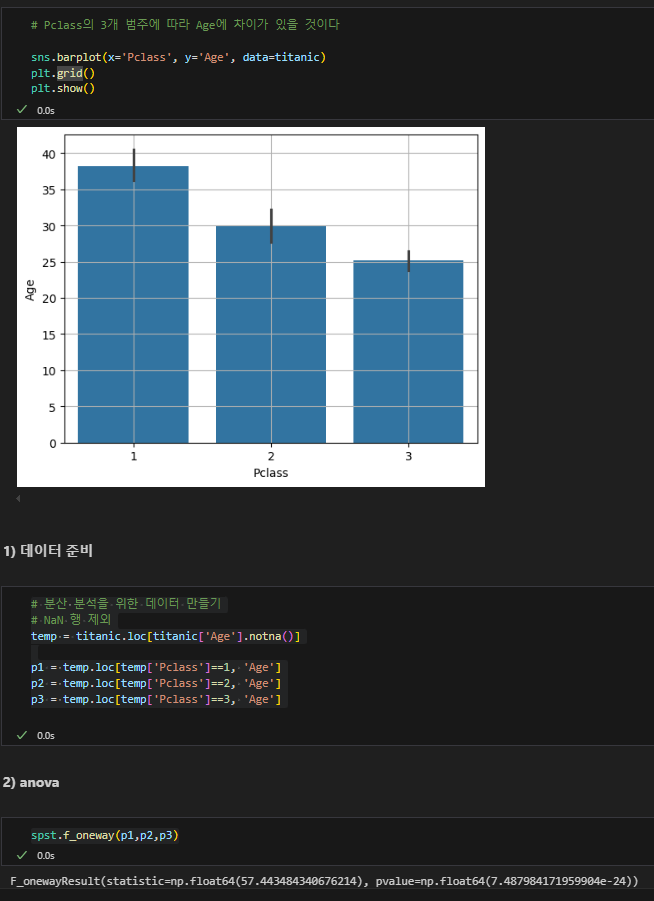
F-statistic 57.443 집단 간 평균차이가 유의미하게 큼.
p-value가 유의미하게 작기 때문에 귀무가설을 기각.

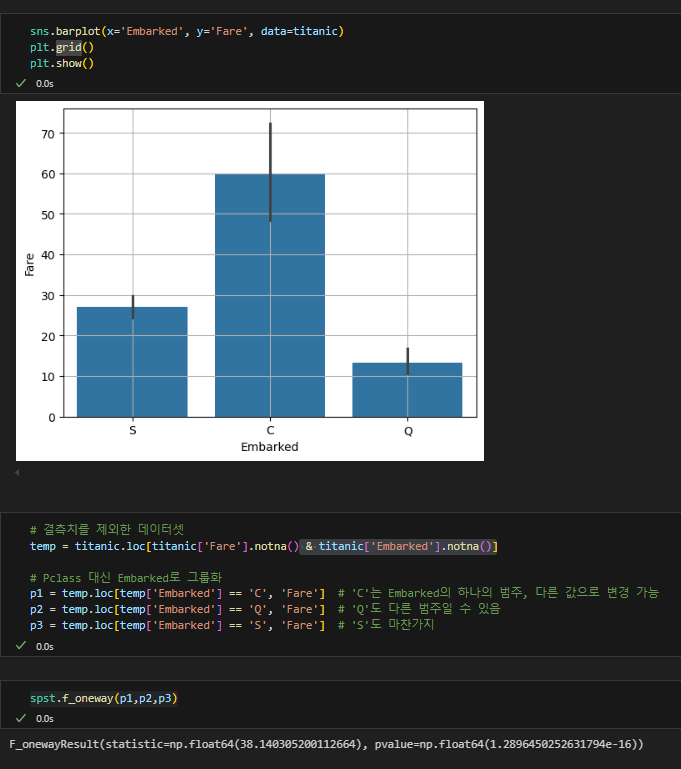
승선지와 운임 차이

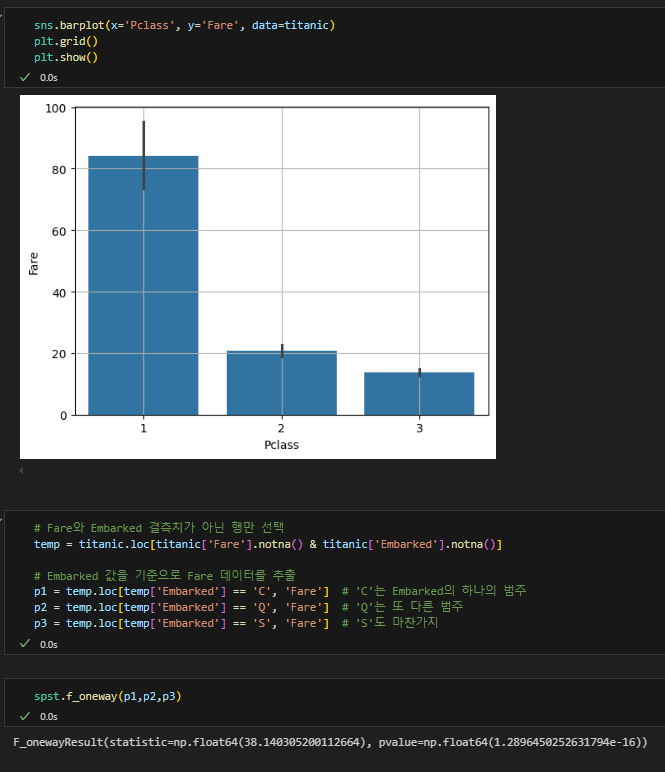
객실등급과 운임 차이

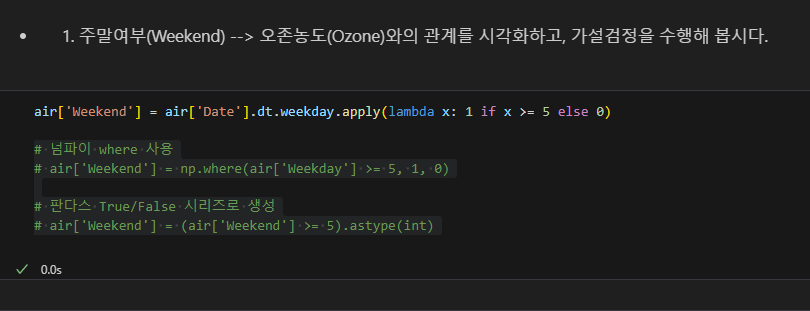
주말 여부와 오존의 분산 분석

주말 여부 열 생성

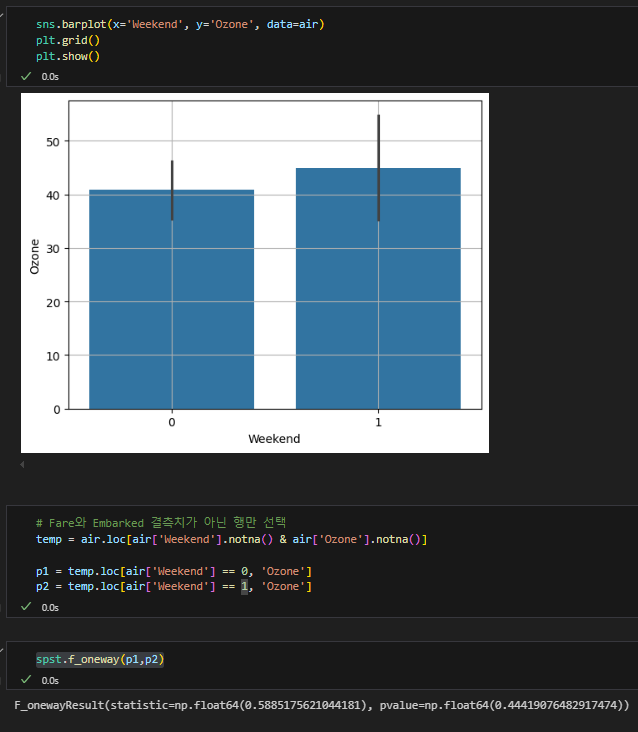
귀무가설 채택.

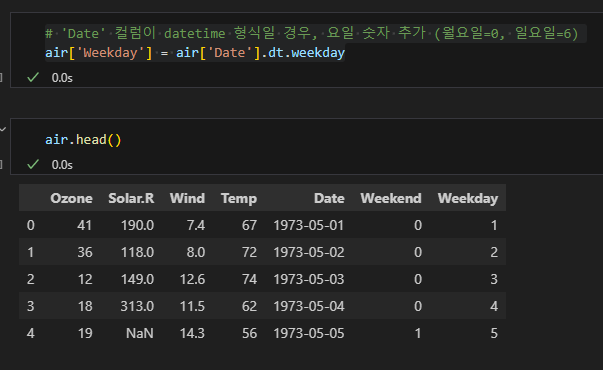
요일 숫자로 열 생성

요일별 오존의 분산 분석

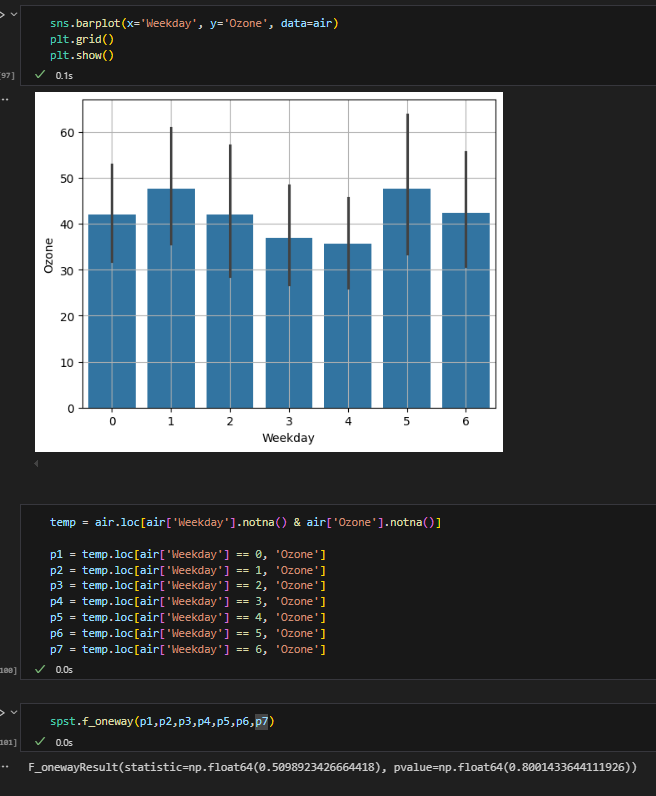
귀무가설 채택.

월별 오존의 분산 분석

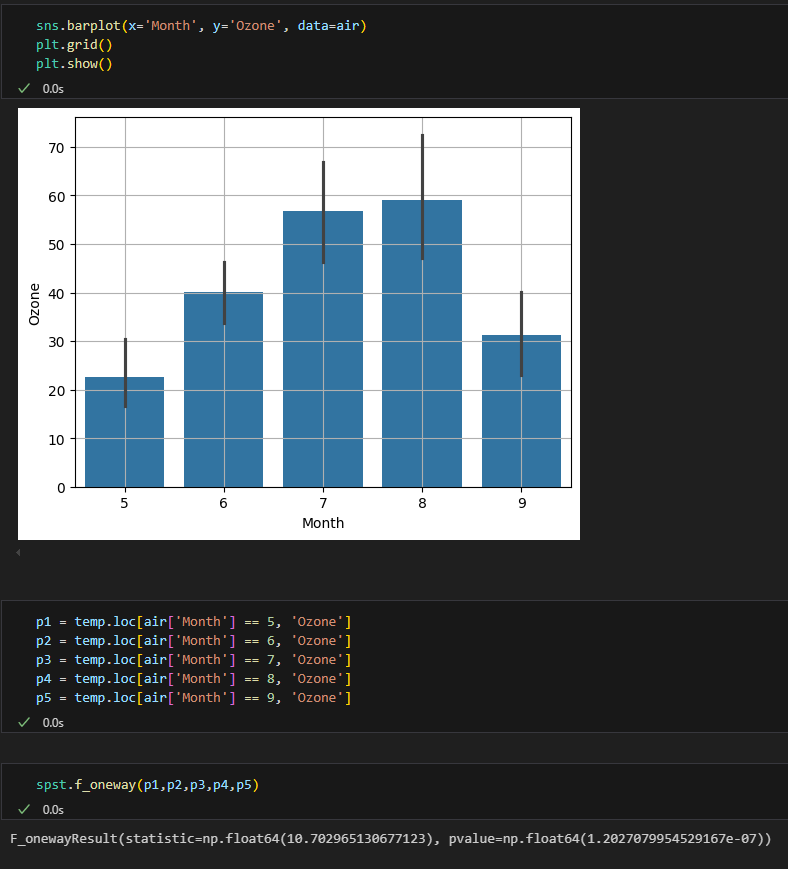
귀무가설 기각.

오차막대 : SEM (Standard Error Mean 표준오차)를 시각화.

SE(표준 오차) 구하기
t-검정에서 오차(표준오차, SE)는 statistic 값과 그룹 평균을 알고 있을 때 계산 가능.
ANOVA에서 오차(그룹 내 변동성)는 F-statistic과 관련된 MS 값들을 알면 계산할 수 있음.

anova에서 구한 그룹 내 변동성으로 표준오차를 구할 수 있다.

실습
carsheat Sales 변수(타깃)에 대하여 각 변수의 유의도 측정하기.

참고
상관계수(r) : -1 혹은 1에 가까울수록 유의
p-value : 0.05 이하 유의
t 값 : -2보다 작거나, 2보다 크면 유의

참고
spst.pearsonr()은 함수는 Series 객체나 array-like 객체 (예: 리스트, 배열 등)를 기대함. SciPy는 숫자 리스트나 NumPy 배열을 사용한다.

그런데 실수로 문자열을 인자로 전달했더니 튜플로 인식하였음.

그 이유는 파이썬의 기본 동작 때문. 파이썬에서 문자열(string)은 시퀀스 타입의 하나로, 개별 문자들의 반복 가능한(iterable) 컬렉션임. 따라서 문자열을 함수에 전달할 때, 각 문자가 별도의 요소로 취급됨.

이렇게 되는 이유는:
pearsonr 함수(SciPy 라이브러리)는 두 개의 동일한 길이를 가진 시퀀스를 기대함.
문자열은 시퀀스이므로 각 문자가 개별 데이터 포인트로 해석됨.
각 문자는 내부적으로 ASCII/Unicode 값으로 변환되어 계산에 사용됨.

튜플의 핵심 특징:
불변성(immutable) - 한번 생성되면 내용을 수정할 수 없다.
소괄호 () 사용 (리스트는 대괄호 [] 사용)
메모리를 더 적게 사용
딕셔너리의 키로 사용 가능 (리스트는 불가능)

profile
sottuggung
hello world
이전 포스트

day 036 KPMG Future Academy

다음 포스트

day 038 KPMG Future Academy

0개의 댓글