KPMG Future Academy AI 활용 데이터 분석가 3기 38일차 수업을 2025년 1월 10일에 참석했다.
- 이변량 분석 : 범주(이산형) vs. 숫자
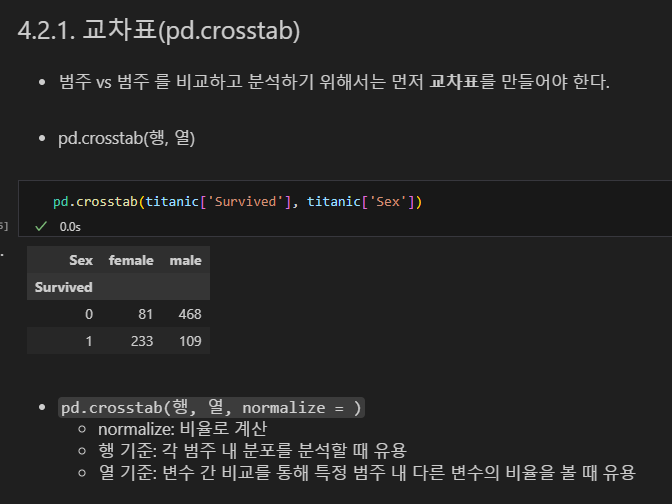
1.1. 교차표, 모자이크, 100% Stacked Bar
1.2. 수치화 : 카이제곱 검정 - 이변량 분석 : 숫자 vs. 범주
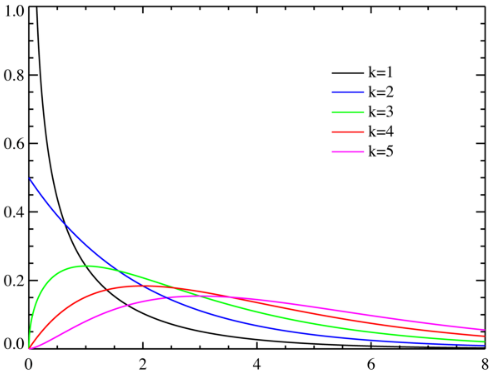
2.1. 확률밀도 함수, 누적 분포도
1. 이변량 분석 : 범주(이산형) vs. 숫자
1.1. 교차표, 모자이크, 100% Stacked Bar
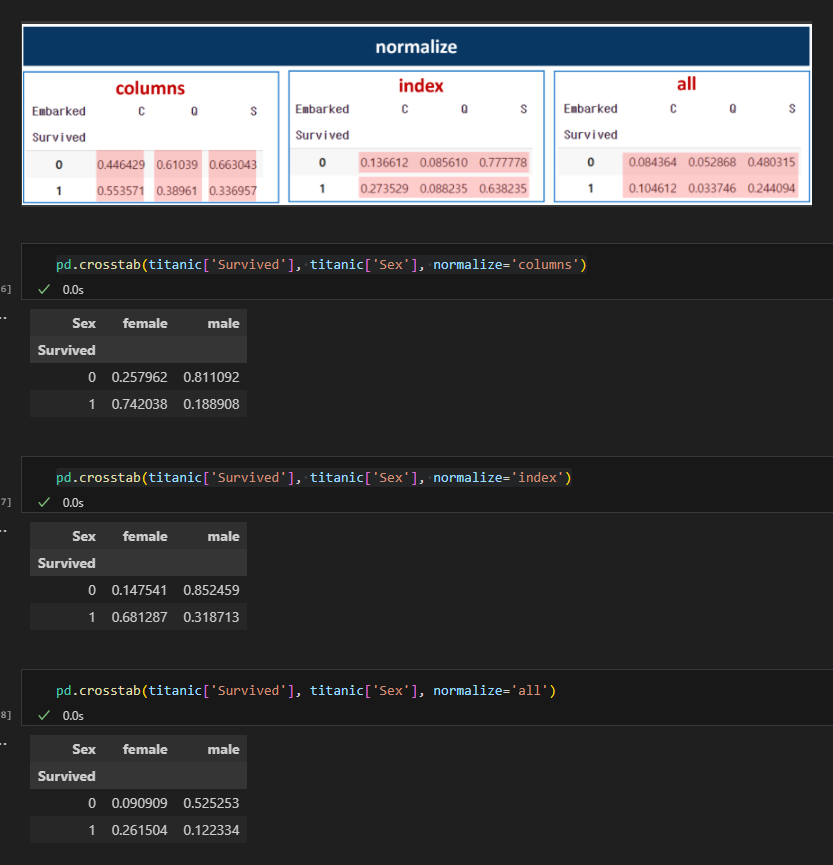
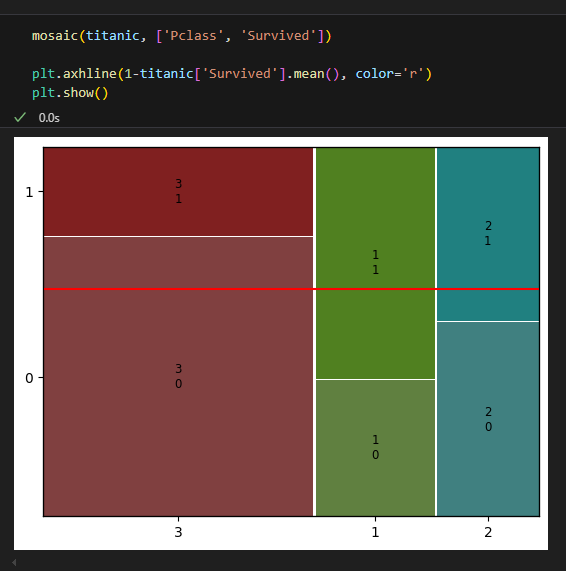
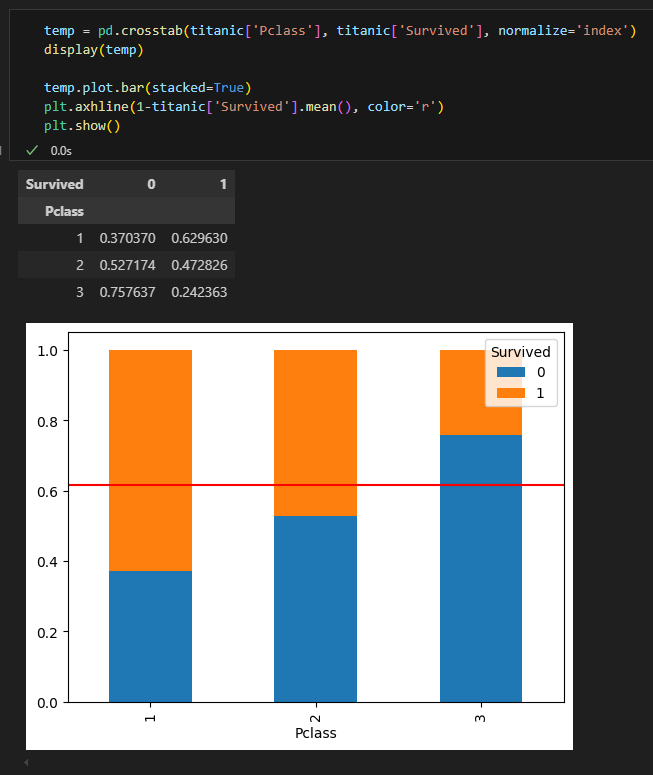
① X축 길이는 각 객실등급별 승객비율을 나타낸다.
② 그 중 3등급 객실에 대해서 보면, y축의 길이는, 3등급 객실 승객 중에서 사망, 생존 비율을 의미한다.
1.2. 수치화 : 카이제곱 검정
- 카이제곱검정 : 범주형 변수들 사이에 어떤 관계가 있는지, 수치화 하는 방법
-
카이 제곱 통계량
- 계산 목적: 관측값(실제 데이터)과 기대값(관계가 없다고 가정했을 때의 값)의 차이를 측정하여, 두 범주형 변수 사이에 연관성이 있는지 확인함.
- 클수록 기대빈도로부터 실제 값에 차이가 크다는 의미.
- 계산식으로 볼 때, 범주의 수가 늘어날 수록 값은 커지게 되어 있음.
- 보통, 자유도의 2~3배 보다 크면, 차이가 있다고 본다.
-
범주형 변수의 자유도 : 범주의 수 - 1
-
카이제곱검정에서는
- x 변수의 자유도 × y 변수의 자유도
- 예 : Pclass --> Survived
- Pclass : 범주가 3개, Survived : 2개
- (3-1) * (2-1) = 2
- 그러므로, 2의 2 ~ 3배인 4 ~ 6 보다 카이제곱 통계량이 크면, 차이가 있다고 볼수 있음.
카이제곱 통계량, p-value, 자유도, 기대빈도
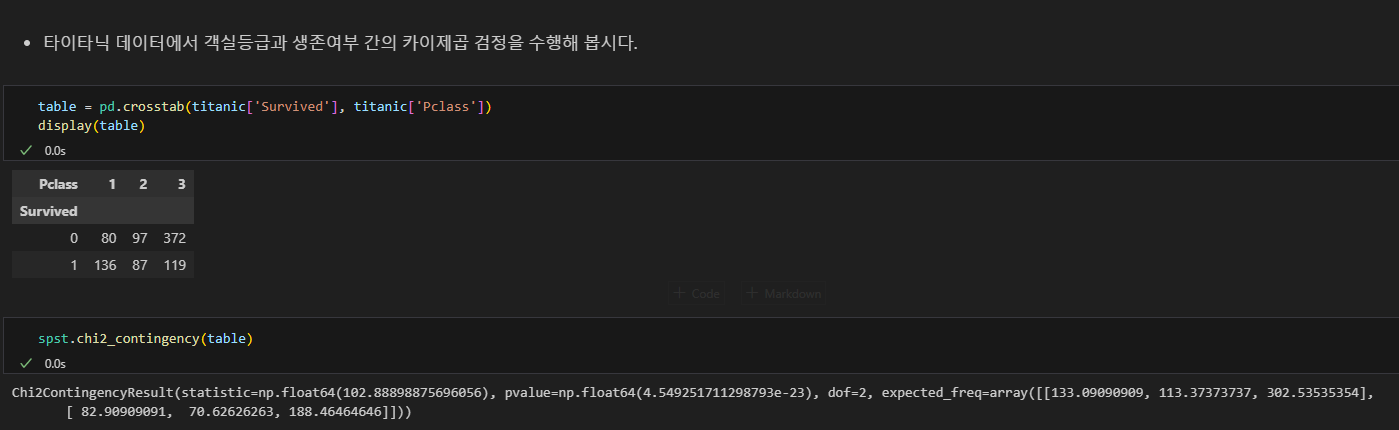
카이제곱 통계량 : 값이 클수록 두 변수 간 연관성이 강하다.
p-value : 귀무가설(두 변수는 독립이다)을 기각할 수 있음.
자유도 :
기대빈도(expected frequencies) :
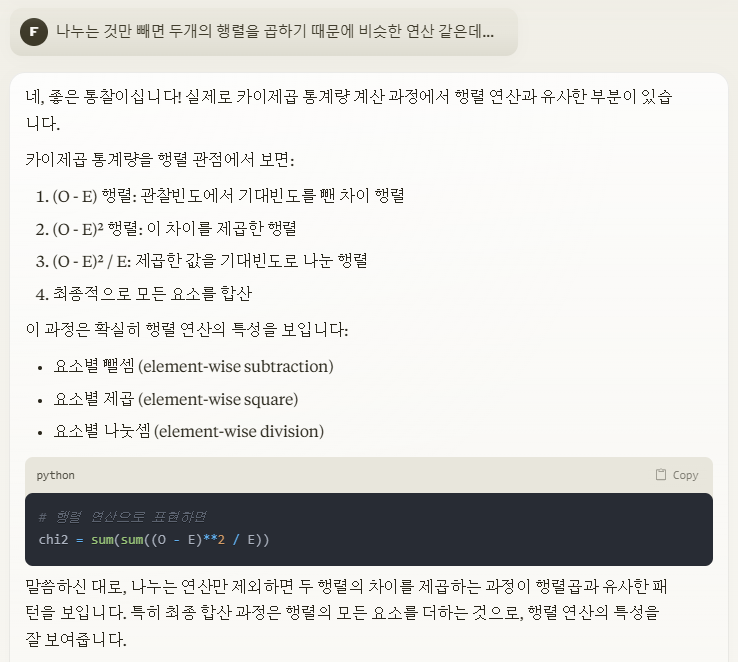
즉, 셀별로 독립적인 계산을 하고 그 결과를 모두 더하는 스칼라 값을 얻는 과정.
Claude 3.0과의 숨막히는 티키타카

2. 이변량 분석 : 숫자 vs. 범주
2.1. 확률 밀도 함수, 누적 분포도
-
시각화 : kde Plot, Histogram
- 범주별 분포로 비교하는 그래프 그리기
- 범주별 비율로 비교하는 그래프 그리기
-
kdeplot을 그리는 두 가지 방법이 있다.
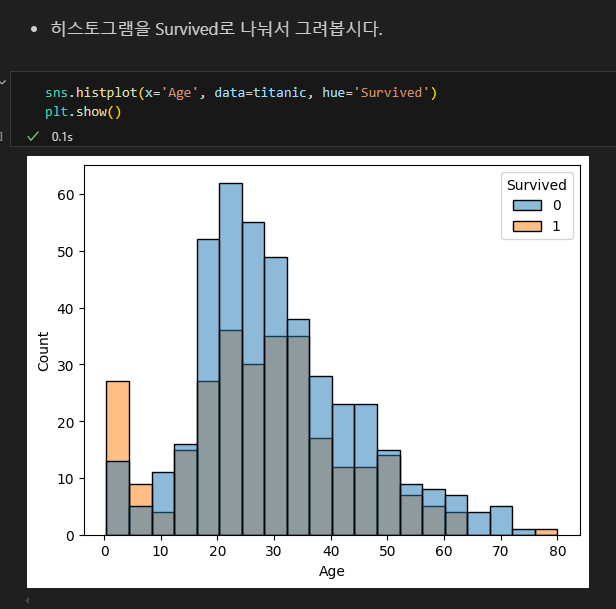
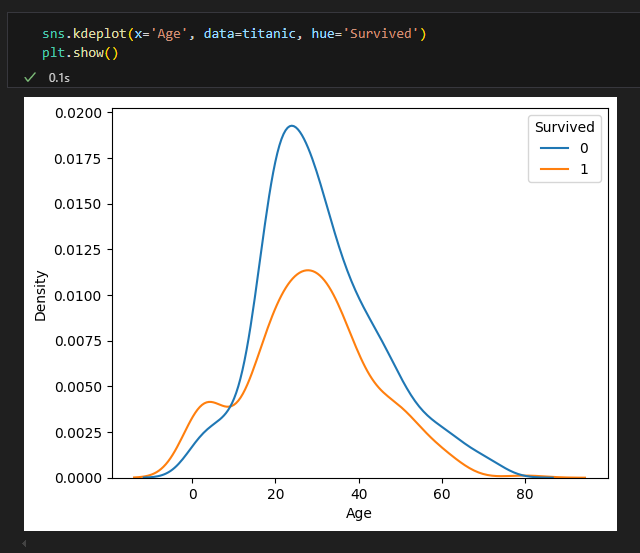
- ① kdeplot( , hue = 'Survived')
- 생존여부의 비율이 유지된 채로 그려짐
- 두 그래프의 아래 면적의 합이 1
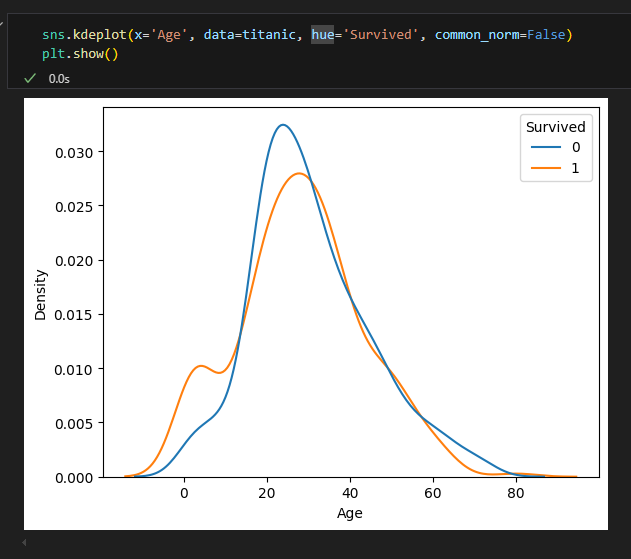
- ② kdeplot( , hue = 'Survived', common_norm = False)
- 생존여부 각각 아래 면적의 합이 1인 그래프
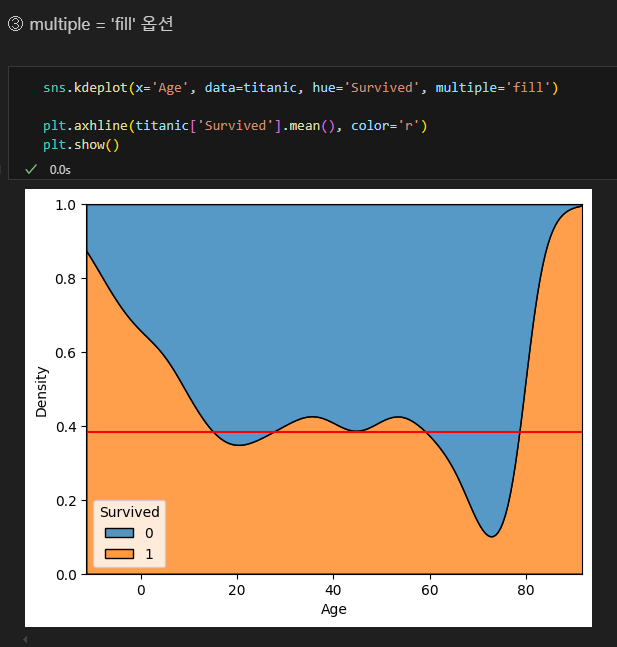
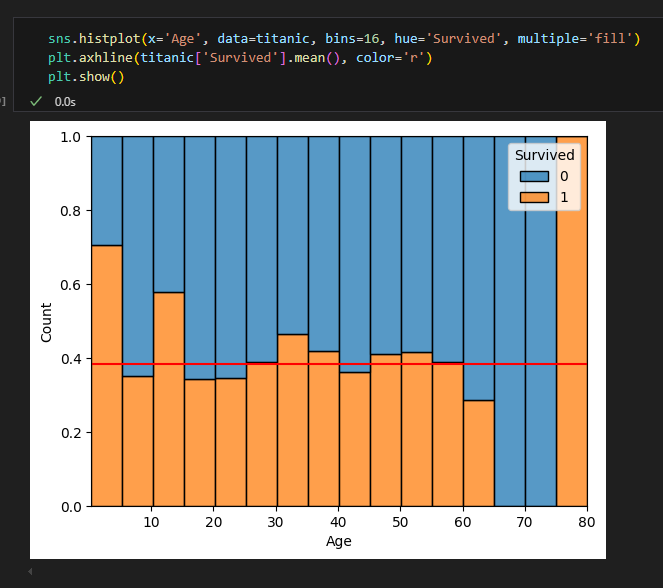
- ③ kdeplot( , hue = 'Survived', multiple = 'fill')
- 나이에 따라 생존여부 비율을 비교해볼 수 있음. (양의 비교가 아닌 비율!)
- ① kdeplot( , hue = 'Survived')
① kdeplot( , hue = 'Survived)
- common_norm = True (기본값)
- common_norm: 그래프 안쪽 넓이가 True면 합쳐서 1, 아니면 각각 넓이가 1
절대값
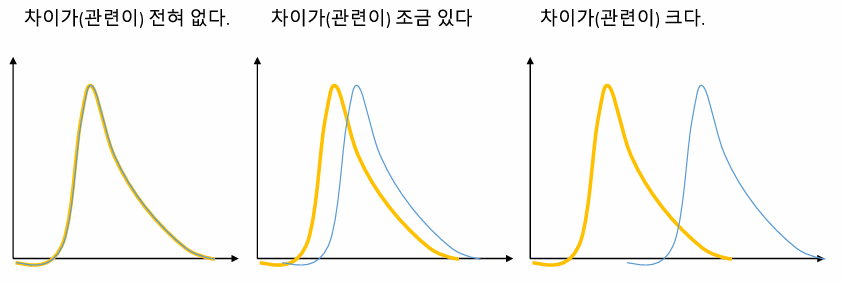
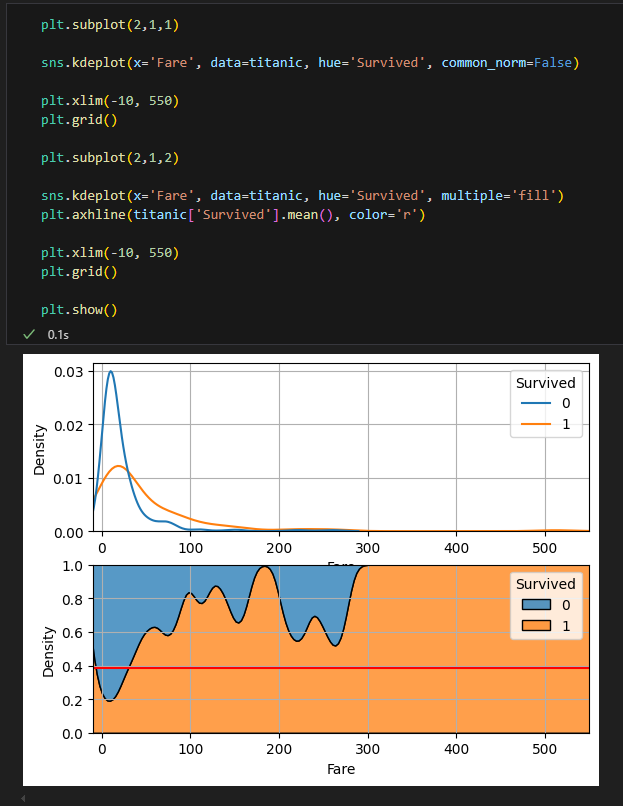
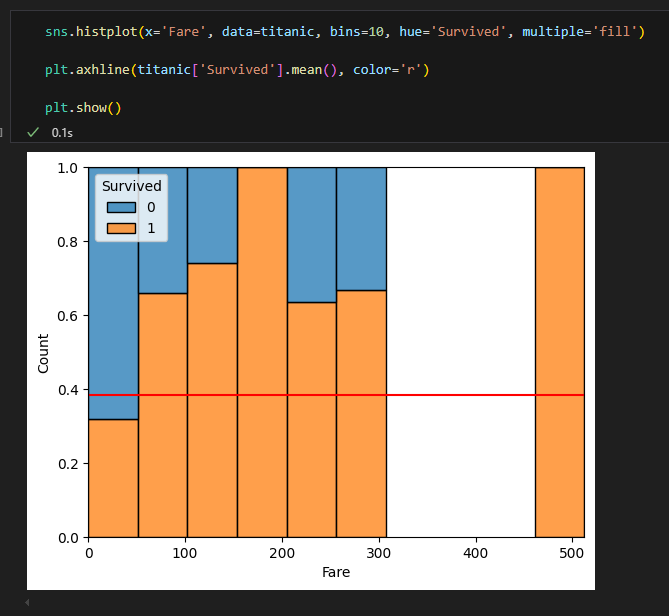
이 두 차트는 타이타닉 승객의 요금(Fare)과 생존 여부(Survived)의 관계를 보여주는 분포도
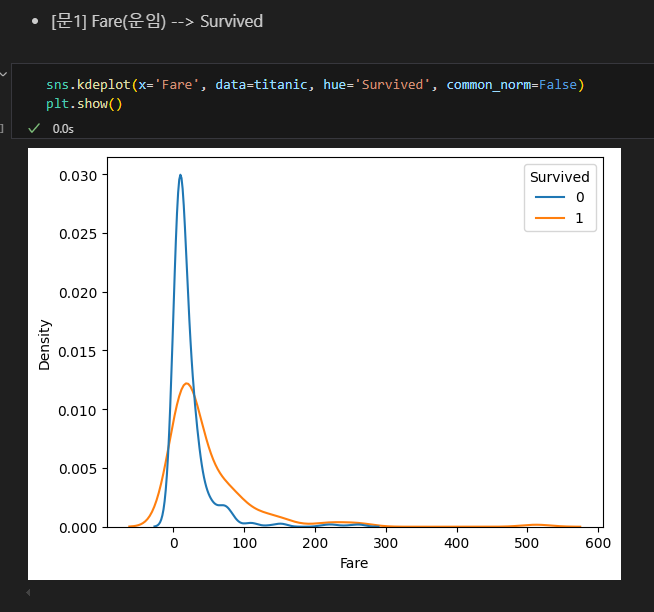
상단 차트 (Density Plot):
승객 요금(x축)에 따른 밀도(y축)를 보여줌
파란선(0)은 사망자, 주황선(1)은 생존자의 분포
낮은 요금대(0-100)에서 가장 높은 밀도를 보이며, 특히 사망자(0)의 밀도가 더 높음
고액 요금대로 갈수록 밀도가 급격히 감소합니다
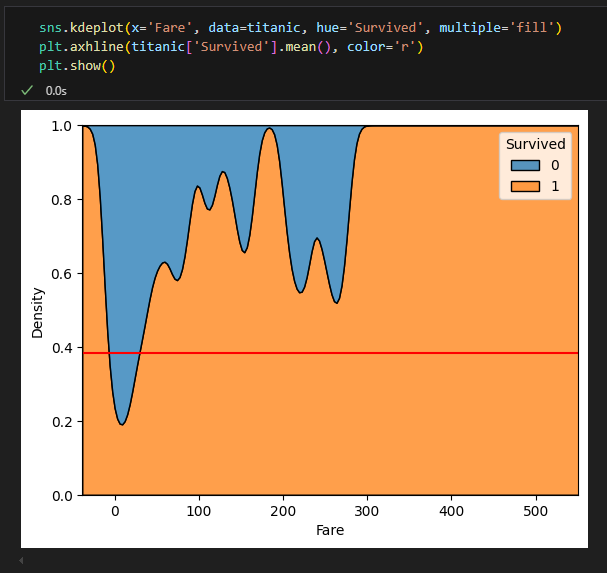
하단 차트 (누적 분포도):
요금대별 생존자와 사망자의 비율을 보여줌
y축의 1.0은 전체(100%)를 의미함
주황색 영역(1)은 생존자, 파란색 영역(0)은 사망자 비율
대체로 요금이 높아질수록 생존 비율(주황색 영역)이 증가하는 경향을 보임
특히 300달러 이상의 고액 요금대에서는 생존률이 매우 높음
전체적인 해석:
대부분의 승객은 저가 티켓을 구매
고가 티켓 승객들의 생존률이 더 높음
이는 티켓 가격이 좌석 등급과 연관되어 있으며, 상위 등급 승객들이 생존에 유리했을 것임을 시사