OpenGL을 사용함에 있어서 필요한 벡터와 매트릭스에 대한 개념을 어느 정도 복기하자.
공대를 나온 사람(나포함)은 단순히 복습 느낌으로 한 번 간단히만 보고 넘어가면 될 것 같다.
실제로 숫자 계산 자체를 직접하지는 않는다. 대부분 OpenGL Math Library가 해주지만 하지만 효율적인 그래픽 프로그래머가 되기 위해서는 화면 뒤에서 무슨 일이 일어나는지 이해하고 있는 것이 굉장히 중요하고 이번에 다루는 수학적 개념은 이해하는데에 있어 도움이 될 것이다.
Vector
크기와 방향을 갖는 물리량을 벡터라고 한다
벡터를 표현하는 방식은 아래와 같다. (XYZ 좌표계 기준)
- x = 4, y = 6, z = 2
- v = [4, 6, 2]
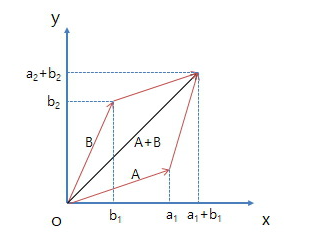
벡터 간의 덧셈과 뺄셈도 가능하다. 덧셈과 뺄셈은 벡터 간 요소들 간의 연산을 진행하면 된다.
덧셈
뺄셈**
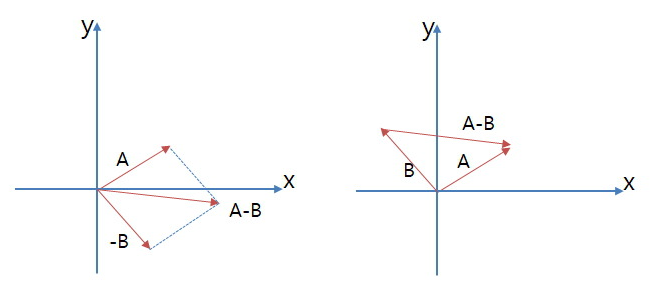
벡터의 곱셈도 가능하다.
곱셈 - Scalar
Scalar 곱은 단순히 크기에 곱해주기만 하면 된다. 모든 원소들에 동일한 상수를 곱하는 과정
Dot Product
개념면에서 중요한 것중 하나가 Dot Prouct 다른 명칭으로는 Scalar Product라고 불리는데 이는 결과가 벡터로 나오는 것이 아니라 상수로 나오기 때문이다.
두 개의 벡터 V = [a, b, c], U =[d, e, f]가 있을때 Dot Product를 하는 방법은 두 가지가 있다.
-
[a, b, c] * [d, e, f] = a*d + b*e + c*f -
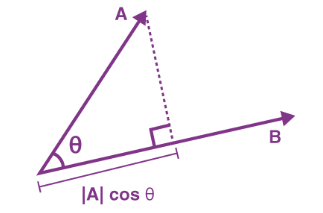
V * U = |V| * |U| * cos(θ)
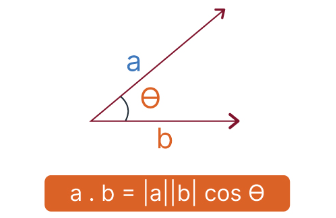
|U| * cos(θ)는 U벡터를 V 벡터에 내적을 시킨 다음 벡터의 크기와 V의 크기를 곱한 것과 동일하다.
크기
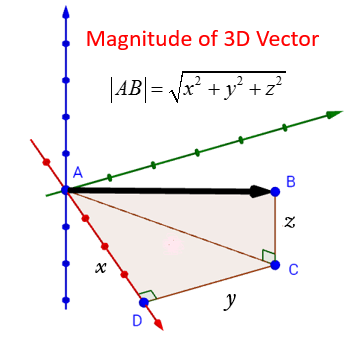
크기는 모든 원소들의 제곱의 합에 제곱근을 구하면 된다.
|V| = sqrt(x^2+ y^2 + z^2)
피타고라스 정리를 이용하는 것이다. 잘 이해가 안된다면 아래 그림을 참고하자.
따라서 cos(θ) = v * U / |V| * |U| 를 계산할 수 있다.
이는 쉽게 말해 첫번째 방법으로 Dot Product를 수행한 값을 기반으로 두 벡터의 사이 긱도도 알 수 있다는 뜻이다. (벡터에 대한 값들만 있으면, Dot Product과 크기 계산이 가능하기 때문에!)
두 벡터 사이의 각도를 알 수 있다는 것은 굉장히 중요한 개념이다. 반사된 빛이 사용자의 눈에 비춰지는 각도인지, 어떤 오브젝트가 사용자의 시야 각도 내에 들어오는지 등, 등 이런 것을 확인할 수 있게 된다.
단위 벡터
길이가 1인 벡터, 방향 벡터라고도 한다.
벡터의 각 원소들을 벡터의 크기로 나눠주면 단위 벡터로 만들 수 있다.
내적
내적은 쉽게 말해 한 벡터를 다른 벡터 위로 수직으로 내리는 것이다.
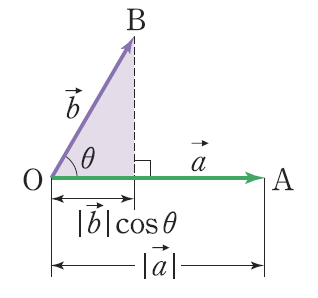
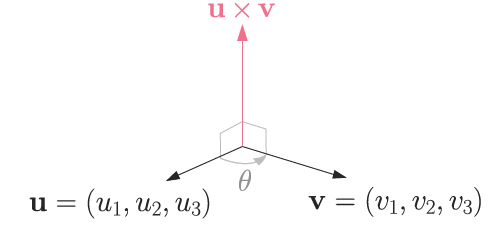
외적
두 벡터로 두 벡터에 수직인 벡터를 얻을 수 있다. Cross Product라고도 부른다.
Matrix
i * j 형태의 값들의 모임 ( i = 행(rows), j = 열(columns)
매트릭스는 게임 개발이나 그래픽에서뿐만 아니라 과학 분야에서도 많이 활용된다. 위치 정보에 특별히 사용할 필요는 없다. 실제 위치 좌표보다는 데이터 컨테이너와 같은 역할로 많이 사용한다. 모델 변환과 프로젝션을 처리하는데 이러한 매트릭스가 사용된다.
덧셈, 뺼셈
벡터와 동일하게 각 자리의 원소들끼리 덧셈과 뺄셈을 수행한다.
곱셈
곱셈은 행렬 곱이라고도 하는데 아래 사진을 보면 이해하기가 쉽다.
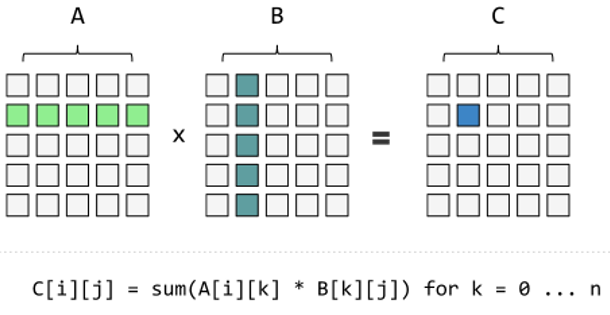
이처럼 행렬 간의 곱은 A와 B의 행과 열을 각각 뽑아서 Dot Product를 하고 적절한 위치에 넣는 방식이다. 그렇기에 A와 B 행렬의 순서가 바뀌면 전혀 다른 값이 된다.
- 곱하는 행렬의 크기도 i * k , k * j에서 처럼 행의 수와 열의 수가 맞아야 곱할 수 있다.
- 결과 행렬의 크기도 i * j로 바뀐다.
그럼 행렬이 벡터와 함께 어떻게 작동할까?
벡터는 단순히 하나의 열로 구성된 행렬이라고 간주하고 다른 행렬과 계산이 가능하다.
Translation
벡터를 움직이는 행렬 연산, 어떤 것의 위치를 바꿀 때 사용
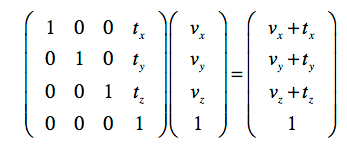
Scaling
벡터의 크기를 변경할 때 사용하는 행렬 연산, 거리를 증가 시키거나, 오브젝트의 크기를 수정할 때 사용한다.
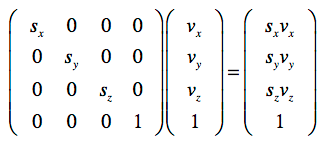
실제로 이러한 벡터 Scaling이 자주 사용되지는 않는다. 이런식으로 크기를 키우면 표면이 부드럽지 않고 그래픽이 부정확하기 때문이다.
Rotation
벡터를 회전시킬 때 사용하는 행렬 연산, 말 그대로 방향을 바꾸거나 오브젝트를 회전 시킬 때 사용한다.
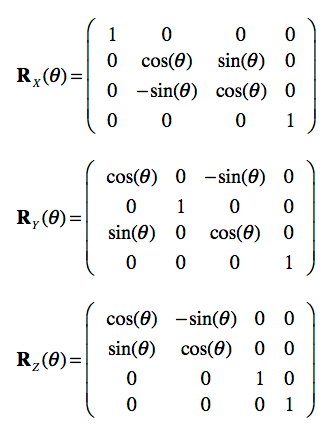
각각 회전하고자 하는 축의 행렬과 벡터를 곱하면 된다.
2D 게임은 주로 z 회전, 3D 게임은 x, y 회전을 많이 사용한다.
Combining
두 행렬을 곱해준 다음에 벡터에 곱해주면 두 transform을 결합할 수 있다.
중요한 점은 행렬 곱이 들어가기 때문에 곱해주는 순서가 중요하다!
GLM
OpenGL Mathematics(GLM)은 OpenGL Shading Language(GLSL)을 기반으로 하는 그래픽스 소프트웨어에서 사용할 수 있는 C++수학 라이브러리이다 이 라이브러리가 제공하는 클래스와 함수들은 GLSL의 naming convention과 기능들이 유사하기 때문에 GLSL을 아는 사람이라면 C++을 이용하여 GLM도 쉽게 사용할 수 있다. 중요한 점은 vec4, 그리고 mat4(4x4) 타입을 사용한다는 점이다.
- GLM is a free library for handling common mathematical operations used with openGL
Simple Code
glm::mar4 trans;
trans = glm::translate(trans, glm::vec3(1.0f, 2.0f, 3.0f));Uniform Variable
vertex 별로 다른 값을 갖는 attribute와 다르게 전체 primitive에 동일하게 적용되는 속성을 uniform이라고 한다. 즉, 특정 vertex와 연결되지 않은 셰이더의 전역 값이라고 할 수 있다.
만약 물체 전체를 움직이려면 모든 vertex 별로 동일한 방향으로 이동해한 후의 값을 계산해야되는데, uniform Value를 이용해 어떤 값을 전달하면 모든 vertex에 동일하게 적용시킬 수 있다. (위치 이동 뿐만 아니라 회전, 크기에도 사용 가능하다)
유니폼 선언
#version 330
in vec3 pos;
uniform mat4 model;
void main() {
gl_Position = model * vec4(pos, 1.0);
}shader에서는 이러한 변수 선언 시 uniform 변수를 넣는 것으로 선언이 가능하다. uniform 변수는 셰이더에 위치 ID를 가지게 된다. 위 코드를 보면 셰이더 내부에 mat4 타입의 model이라는 uniform 변수가 선언되있다.
선언했지만 쓰니 않는 유니폼은 최적화 과정에서 없어질 수 있다.
유니폼의 location 찾기
쉐이더 ID(uniform value의 위치)를 알아야 연결 시켜줄 수 있다.
int location = glGetUniformLocation(ShaderID, "uniformVarName");유니폼의 값 설정
유니폼의 값 설정하기
glUniform\[1/2/3/4]\[f/i/ui](location, ...value1, value2, ..., valueN) // value의 개수는 1/2/3/4에 일치uniform float time; // glUniform1f(location, value)
uniform int index; // glUniform1i(location, value)
uniform vec4 color; // glUniform4f(location, v1, v2, v3, v4)
uniform bool flag; // glUniform1i(location, value)이외에도 유니폼의 실제 사용은 이후에 코드로 직접 다뤄보도록 하자.