ISLR 패키지에 포함된 Smarket 데이터셋을 사용하려고 한다.
> install.packages("ISLR")
> library(ISLR)
> str(Smarket)
'data.frame': 1250 obs. of 9 variables:
$ Year : num 2001 2001 2001 2001 2001 ...
$ Lag1 : num 0.381 0.959 1.032 -0.623 0.614 ...
$ Lag2 : num -0.192 0.381 0.959 1.032 -0.623 ...
$ Lag3 : num -2.624 -0.192 0.381 0.959 1.032 ...
$ Lag4 : num -1.055 -2.624 -0.192 0.381 0.959 ...
$ Lag5 : num 5.01 -1.055 -2.624 -0.192 0.381 ...
$ Volume : num 1.19 1.3 1.41 1.28 1.21 ...
$ Today : num 0.959 1.032 -0.623 0.614 0.213 ...
$ Direction: Factor w/ 2 levels "Down","Up": 2 2 1 2 2 2 1 2 2 2 ...이 데이터셋은 2001년 초부터 2005년 말까지 1,250일 동안 S&P 500 지수의 수익률을 나타내고 있다.
Year : 연도
Lag1 ~ Lag5 : 이전 5일의 수익률
Volume : 전날 거래된 주식 수 (10억 단위)
Today : 당일 수익률
Direction : 당일 주가 상승/하락 여부 (Up / Down)
변수들의 상관관계를 파악하기 위해 Correlation Matrix를 출력할건데,
Direction 은 범주형 변수이므로 제외해야 에러가 발생하지 않는다.
> cor(Smarket[, -9])
Year Lag1 Lag2 Lag3 Lag4 Lag5 Volume Today
Year 1.00000000 0.029699649 0.030596422 0.033194581 0.035688718 0.029787995 0.53900647 0.030095229
Lag1 0.02969965 1.000000000 -0.026294328 -0.010803402 -0.002985911 -0.005674606 0.04090991 -0.026155045
Lag2 0.03059642 -0.026294328 1.000000000 -0.025896670 -0.010853533 -0.003557949 -0.04338321 -0.010250033
Lag3 0.03319458 -0.010803402 -0.025896670 1.000000000 -0.024051036 -0.018808338 -0.04182369 -0.002447647
Lag4 0.03568872 -0.002985911 -0.010853533 -0.024051036 1.000000000 -0.027083641 -0.04841425 -0.006899527
Lag5 0.02978799 -0.005674606 -0.003557949 -0.018808338 -0.027083641 1.000000000 -0.02200231 -0.034860083
Volume 0.53900647 0.040909908 -0.043383215 -0.041823686 -0.048414246 -0.022002315 1.00000000 0.014591823
Today 0.03009523 -0.026155045 -0.010250033 -0.002447647 -0.006899527 -0.034860083 0.01459182 1.000000000상관계수 행렬을 보면 Lag와 Volume은 거의 상관관계가 없다고 보여진다.
유일하게 Year과 Volume 의 상관계수가 0.53으로 양의 상관관계를 갖는다.
즉, 2001년부터 2005년까지 일일 거래 주식 수가 증가하고 있는 것이다.
> attach(Smarket)
> plot(Volume, col = 'blue', pch = 16)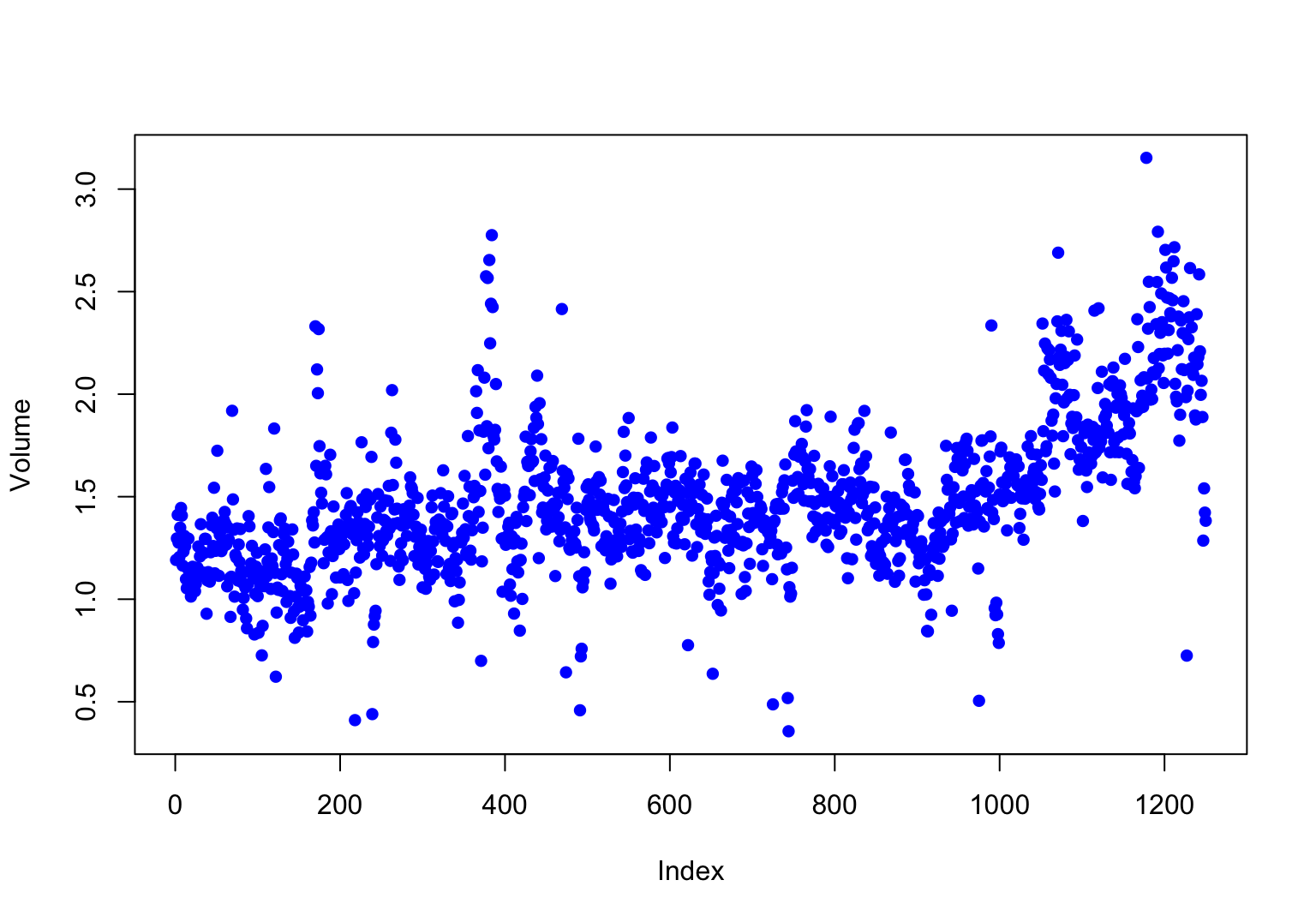
시간에 따른 거래량을 시각화해보면, 조금씩 증가하는 추세가 보인다.
그럼 Direction의 클래스를 예측하기 위해 Logistic Regression Model을 적합해보자.
> glm.fit = glm(Direction ~ . -(Year + Today + Direction), data = Smarket,
+ family = binomial(link = 'logit'))
> summary(glm.fit)
Call:
glm(formula = Direction ~ . - (Year + Today + Direction), family = binomial(link = "logit"),
data = Smarket)
Coefficients:
Estimate Std. Error z value Pr(>|z|)
(Intercept) -0.126000 0.240736 -0.523 0.601
Lag1 -0.073074 0.050167 -1.457 0.145
Lag2 -0.042301 0.050086 -0.845 0.398
Lag3 0.011085 0.049939 0.222 0.824
Lag4 0.009359 0.049974 0.187 0.851
Lag5 0.010313 0.049511 0.208 0.835
Volume 0.135441 0.158360 0.855 0.392
(Dispersion parameter for binomial family taken to be 1)
Null deviance: 1731.2 on 1249 degrees of freedom
Residual deviance: 1727.6 on 1243 degrees of freedom
AIC: 1741.6
Number of Fisher Scoring iterations: 3
적합된 회귀계수들 중 유의한 값은 없어보인다. 그나마 작은 P-Value를 갖는 Lag1도
0.145로 Direction과 연관성이 있다고 말하기는 힘들다.
우선 위에서 만든 분류기의 성능을 측정하기 위해 예측값을 구해보자.
> glm.probs = predict(glm.fit, type = 'response')
> contrasts(Direction)
Up
Down 0
Up 1contrast() 함수를 통해 R이 Up을 1, Down을 0으로 변환했다는 것을 알 수 있다.
따라서 predict() 메서드로 출력되는 값은 주가의 상승 확률을 의미한다.
> glm.pred = rep("Down", nrow(Smarket))
> glm.pred[glm.probs > 0.5] = "Up"주가 상승률이 0.5 보다 크면 Up, 그 이하면 Down으로 예측값을 저장한다.
> table(glm.pred, Direction)
Direction
glm.pred Down Up
Down 145 141
Up 457 507
> mean(glm.pred == Direction)
[1] 0.5216Logistic Regression을 이용한 분류기는 52.16%의 적중률로 임의 분류보다
조금 좋은 정도의 성능을 보여준다. 과연 이 결과를 신뢰할 수 있을까?
어쩌면 학습 데이터셋에 과적합되어 다른 데이터셋에서는 그보다 낮을 성능을 보일지도 모른다.
이번에는 데이터셋을 train set과 test set으로 분할하여 성능 검증을 해보겠다.
일반적으로는 7:3이나 8:2 같이 비율로 분할하지만,
주식 데이터의 특성을 고려하여 2005년 데이터와 그 이전 데이터로 나누기로 했다.
> train = (Year < 2005)
> test = !train # (Year == 2005)
> Smarket.train = subset(Smarket, subset = train)
> Smarket.2005 = Smarket[test,]
> dim(Smarket.2005)
[1] 252 9
> Direction.train = Direction[train]
> Direction.2005 = Direction[test]1250개의 데이터 중 252개의 데이터를 테스트셋으로 분할했다.
이제 훈련 데이터셋을 이용하여 처음과 같은 Logistic Regression 모델을 적합해보자.
> glm.fit = glm(Direction ~ Lag1 + Lag2 + Lag3 + Lag4 + Lag5 + Volume,
+ data = Smarket.train,
+ family = binomial)
> summary(glm.fit)
Call:
glm(formula = Direction ~ Lag1 + Lag2 + Lag3 + Lag4 + Lag5 +
Volume, family = binomial, data = Smarket.train)
Coefficients:
Estimate Std. Error z value Pr(>|z|)
(Intercept) 0.191213 0.333690 0.573 0.567
Lag1 -0.054178 0.051785 -1.046 0.295
Lag2 -0.045805 0.051797 -0.884 0.377
Lag3 0.007200 0.051644 0.139 0.889
Lag4 0.006441 0.051706 0.125 0.901
Lag5 -0.004223 0.051138 -0.083 0.934
Volume -0.116257 0.239618 -0.485 0.628
(Dispersion parameter for binomial family taken to be 1)
Null deviance: 1383.3 on 997 degrees of freedom
Residual deviance: 1381.1 on 991 degrees of freedom
AIC: 1395.1
Number of Fisher Scoring iterations: 3
특별히 p-value에 변화가 있는 것으로 보이진 않는다.
> glm.probs = predict(glm.fit, newdata = Smarket.2005, type = "response")
> glm.pred = rep("Down", nrow(Smarket.2005))
> glm.pred[glm.probs > 0.5] = "Up"
> table(glm.pred, Direction.2005)
Direction.2005
glm.pred Down Up
Down 77 97
Up 34 44
> mean(glm.pred == Direction.2005)
[1] 0.4801587우선 혼동행렬을 보면 상대적으로 오분류율이 높아졌고, 분류기의 적중률도 48.01%로 임의 분류보다 떨어지는 성능을 보인다.
이번에는 비교적 p-value가 낮았던 Lag1과 Lag2만을 사용하여 모델을 적합해보자.
> glm.fit = glm(Direction ~ Lag1 + Lag2, data = Smarket.train, family = binomial)
> glm.probs = predict(glm.fit, Smarket.2005, type = "response")
> glm.pred[glm.probs > 0.5] = "Up"
> table(glm.pred, Direction.2005)
Direction.2005
glm.pred Down Up
Down 35 34
Up 76 107
> mean(glm.pred == Direction.2005)
[1] 0.5634921이 분류기의 적중률은 56.35%로 비교적 좋은 성능을 보이는데, 아마도 Direction과 관계없는 변수들을 삭제하는 것으로 성능을 개선할 수 있을 것으로 예상된다.
