[R] Linear Model Selection

Extension of Linear Models

지금까지 선형 회귀모형을 적합할 때 Least Squares Methods를 이용했다. 하지만 이를 대체할 다른 방법들 역시 존재한다.

• Prediction Accuracy
• Model Interpretability

$n$이 $p$보다 충분히 크지 않을 경우, 최소제곱추정량:LSE은 분산이 크고 과적합되는 경향이 있다. 이런 경우 Test Data에 대한 성능이 매우 떨어질 것이다. 또한 $p$가 $n$보다 크면 LSE가 존재하지 않는다.

추정된 회귀 계수를 제한하거나 축소시키면 Bias가 약간 증가하는 대가로 분산을 크게 줄일 수 있다.
그리고 관련 없는 변수의 회귀 계수를 0으로 설정하면 해석이 쉬운 모형을 얻을 수 있다.

Subset Selection

Best Subset Selection

$p$개의 설명변수의 모든 가능한 조합 각각에 대해 최소제곱법을 사용하여 적합한다.

즉 $2^p$개의 Model 중에서 best Model을 선택한다. 그 절차는 다음과 같다.

1. $M_0$는 영 모형:null model로, 설명변수를 전혀 포함하지 않는 모형이다. 이 모형은 단순하게 각 관측치의 표본평균을 예측한다.
2. $k=1,2,...,p$에 대해
   a. 정확히 $k$개의 예측변수를 포함하는 모든 $p \choose k$개의 모델을 적합시킨다.
   b. 이 $p \choose k$개의 모델 중에서 가장 좋은 모델을 선택하고, 이를 $M_k$라고 한다. 이때 가장 좋은 모델이란 Training Data로 계산된 가장 작은 잔차 제곱합이나 가장 큰 결정계수($R^2$)를 갖는 모델이다.
3. $M_0$에서 $M_k$까지의 모델들을 CV Test MSE, AIC, BIC, 수정된 결정계수 등으로 비교하여 최적의 모델을 선정한다. >> 이때는 Test Data를 사용한다는 것에 주의하자!
   

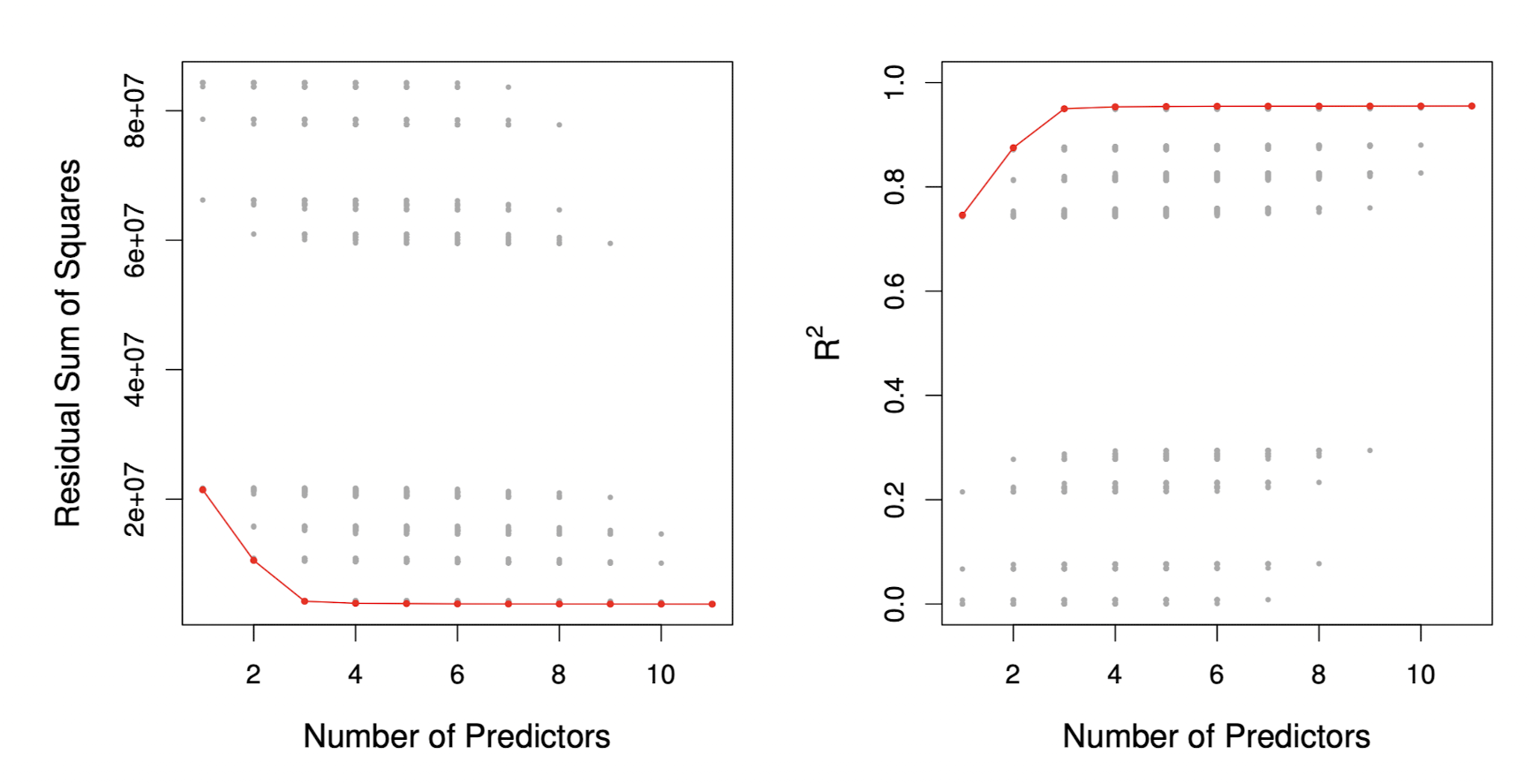
Best Subset Selection을 ISLR 라이브러리의 Hitters 데이터셋에 적용해보자.

> library(leaps)
> regfit.full = regsubsets(Salary ~ ., Hitters, nvmax = 19)
> reg.sum = summary(regfit.full)
> reg.sum$rsq
 [1] 0.3214501 0.4252237 0.4514294 0.4754067 0.4908036 0.5087146 0.5141227 0.5285569 0.5346124 0.5404950 0.5426153 0.5436302 0.5444570 0.5452164 0.5454692
[16] 0.5457656 0.5459518 0.5460945 0.5461159

reg.sum$rsq를 보면 설명변수 1개부터 19개 모델의 결정계수를 출력하고 있다.
16개 변수 이후부터는 큰 변화가 거의 없는 것으로 보아 그 이상으로는 변수를 추가하더라도 설명력이 크게 개선되지 않는다.

> which.max(reg.sum$adjr2)
[1] 11
> which.min(reg.sum$cp)
[1] 10
> which.min(reg.sum$bic)
[1] 6

수정된 결정계수로는 11개, $C_p$로는 10개, BIC로는 6개의 설명변수를 포함한 모델이 가장 좋은 모델로 선택되었다. 가장 작은 6개의 변수를 사용하는 모델의 회귀식을 확인해보자.

> coef(regfit.full,6)
 (Intercept)        AtBat         Hits        Walks         CRBI    DivisionW      PutOuts 
  91.5117981   -1.8685892    7.6043976    3.6976468    0.6430169 -122.9515338    0.2643076 

6개의 설명변수로는 AtBat, Hits, Walks, CRBI, DivisionW, PutOuts가 선택되었다.

Stepwise Selection

Forward Stepwise Selection

Best Subset Selection은 $2^p$개의 모델을 고려해야하므로 $p$가 클때는 사용하기가 힘들다.
Forward Stepwise Selection은 Null Model에서 설명변수를 하나씩 추가하는 방식이다.

따라서 적합되는 모델의 수는 $1+\sum_{k=0}^{p-1} (p-k)=1+\frac{p(p+1)}{2}$.

예를 들어 $p=20$인 경우 Best Subset은 1,048,576개의 모델을 적합해야 하지만, Forward Stepwise은 단 211개의 모델만 적합하면 된다.

이처럼 Forward Stepwise은 비교적 계산이 효율적인 면이 있지만, 최적의 모델을 보장하지는 않는다.

그 예시로 위 표를 보면 1~3개의 변수를 선택할 때는 선택한 변수들이 같지만, 4개를 선택했을 때는 다르다.

Forward Stepwise Selection의 절차는 다음과 같다.

1. $M_0$는 Null Model로, 어떤 설명변수도 포함하지 않는 모델이다.
2. $k=0,1,...,p-1$에 대하여
   a. $M_k$에서 하나의 설명변수를 추가한 $p-k$개의 모든 모형을 고려한다.
   b. 이 중 가장 좋은 모델을 선택하고, 그 모델을 $M_{k+1}$이라 한다. 이때 가장 좋은 모델이란 잔차 제곱합이 가장 작거나 결정계수가 가장 큰 모델을 뜻한다.
3. $M_0,...,M_p$까지의 모델들을 CV Test MSE, AIC, BIC, 수정된 결정계수 등으로 비교하여 최적의 모델을 선정한다.

Forward Stepwise Selection을 R에서 적용해보자.

> regfit.fwd = regsubsets(Salary ~., Hitters, nvmax = 19, method = "forward")
> sum.fwd = summary(regfit.fwd)
> which.max(sum.fwd$adjr2)
[1] 11
> which.min(sum.fwd$cp)
[1] 10
> which.min(sum.fwd$bic)
[1] 6

수정된 결정계수로는 11개, $C_p$로는 10개, BIC로는 6개의 설명변수를 포함한 모델이 가장 좋은 모델로 선택되었다. 이 방법으로도 6개의 설명변수를 갖는 모델을 선택하게 되었다.

Backward Stepwise Selection

Full Model 에서 시작하여 설명변수를 하나씩 제외해 나가는 방식이다.
Forward Stepwise의 반대되는 방식으로, 적합하는 모델의 수는 $1+\frac{p(p+1)}{2}$로 같다.
이 역시 계산 부분에서 효율적이지만, 최적의 모델을 보장하지 않는다.

Backward Stepwise Selection의 절차는 다음과 같다.

1. $M_p$는 Full Model로, 모든 설명변수 $p$개를 포함하는 모델이다.
2. $k=0,1,...,p-1$에 대하여
   a. $M_k$에서 하나의 설명변수를 제외한 $k-1$개의 설명변수를 고려하는 모델을 생각해보자.
   b. 이 $k$개의 모델 중에서 가장 좋은 모델을 선택하고, 그 모델을 $M_{k-1}$이라 한다. 이때 가장 좋은 모델이란 잔차 제곱합이 가장 작거나 결정계수가 가장 큰 모델을 뜻한다.
3. $M_0,...,M_p$까지의 모델들을 CV Test MSE, AIC, BIC, 수정된 결정계수 등으로 비교하여 최적의 모델을 선정한다.

Backward Stepwise Selection을 R에서 적용해보자.

> regfit.bwd = regsubsets(Salary ~., Hitters, nvmax = 19, method = "backward")
> sum.bwd = summary(regfit.bwd)
> which.max(sum.bwd$adjr2)
[1] 11
> which.min(sum.bwd$cp)
[1] 10
> which.min(sum.bwd$bic)
[1] 8

수정된 결정계수로는 11개, $C_p$로는 10개, BIC로는 8개의 설명변수를 포함한 모델이 가장 좋은 모델로 선택되었다. 이 중 가장 작은 8개의 변수를 사용하는 모델의 회귀식을 확인해보자.

> coef(regfit.bwd,8)
 (Intercept)        AtBat         Hits        Walks        CRuns         CRBI       CWalks    DivisionW      PutOuts 
 117.1520434   -2.0339209    6.8549136    6.4406642    0.7045391    0.5273238   -0.8066062 -123.7798366    0.2753892 

8개의 설명변수로는 AtBat, Hits, Walks, CRuns, CRBI, CWalks, DivisionW, PutOuts가 선택되었다.

Hybrid Approaches

위에서 소개한 세 가지 방법들 외에 또 다른 대안으로 Backward Stepwise 와 forward Stepwise의 하이브리드 버전도 있다. 이 방법은 forward Stepwise와 좀 비슷한데, 변수를 추가하다가 더 이상 모델 개선에 영향을 주지 않는 변수를 제거할 수도 있다.

Best Subset Selection을 모방하면서도 Stepwise 의 계산 효율성을 챙길 수 있는 방법이다.

Choosing the Optimal Model

앞에서 소개한 다양한 방법들로 적합한 모델 중, 어떤 모델이 최적의 모델인지를 판단해야한다.
잔차제곱합(RSS)이나 결정계수($R^2$)는 Training Data를 사용하기 때문에 적절한 판단 기준이 아니다.

그래서 사용하는 방법이 $C_p$, AIC, BIC와 수정된 결정계수다.
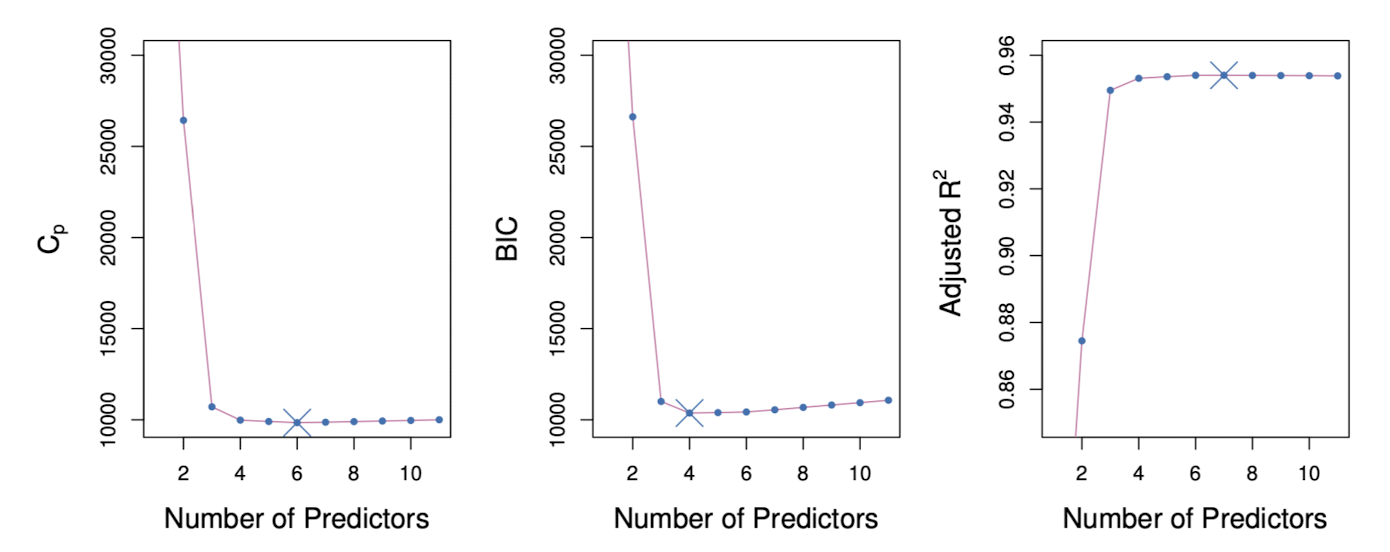
아래 그래프는 Credit 데이터 셋에서 $C_p$, BIC, 수정된 결정계수 값에 따른 최적의 모델을 보여주고 있는데, 그중 BIC는 4개의 변수를 선택한 후 점점 증가하는 것을 볼 수 있다.

반면 나머지 두 그래프는 4개의 변수가 포함된 후 상대적으로 평평한 추세를 보인다.

$C_p$

$d$개의 설명변수를 포함하며 최소제곱법으로 적합된 모델에 대해, $C_p$의 Test MSE 추정치는 다음의 식을 통해 계산된다.

이 통계량은 Training Data으로 추정한 RSS에 $2d\hat\sigma^2$이라는 패널티를 추가하여 RSS가 Test Data를 과소추정하는 문제를 해소한다.

AIC

AIC는 최대가능도함수를 이용하여 적합된 모델에 대해 계산한 값으로, 다음과 같이 주어진다.

데이터의 오차($\epsilon$)가 가우시안 분포를 따른다고 할 때, MLE와 LSE가 같다.
위 식에서 상수 부분은 생략했는데, 이 경우 $C_p$와 AIC는 equivalent이므로 같은 형태를 갖는다.

BIC

$d$개의 설명변수를 갖는 최소제곱법으로 적합한 모델에 대해 BIC는 다음과 같이 주어진다.

$C_p$와 AIC랑 비슷하게 Test Error가 낮을수록 작은 값을 갖기 때문에 BIC가 가장 작은 모델을 선택한다. 패널티로 $2d\hat\sigma^2$ 대신 $log(n)d\hat\sigma^2$를 사용하므로, 설명변수가 많아짐에 따라 더 큰 패널티를 부여한다.

Adjusted $R^2$

수정된 결정계수는 서로 다른 개수의 설명변수를 갖는 모델들을 비교할 때 사용되는 좋은 방법이다.
결정계수는 설명변수의 수가 늘어나면 항상 증가하는 반면, 수정된 결정계수는 불필요한 변수가 포함되는 경우에는 늘어나지 않을 수도 있다. 그 식은 다음과 같이 표현된다.

Validation and Cross-Validation

과거에는 모델에 포함된 변수의 수($p$) 혹은 데이터셋의 크기($n$)가 큰 문제에서 교차검증을 하는 것이 힘들었기 때문에 $C_p$, AIC, BIC, Adjusted $R^2$와 같은 방법들을 선호했다.

하지만 요즘은 컴퓨터 성능이 좋아져 직접적인 Test Error도 계산할 수 있고, 모델에 대한 가정도 적은 교차검증이 매력적인 방법으로 떠오른다.

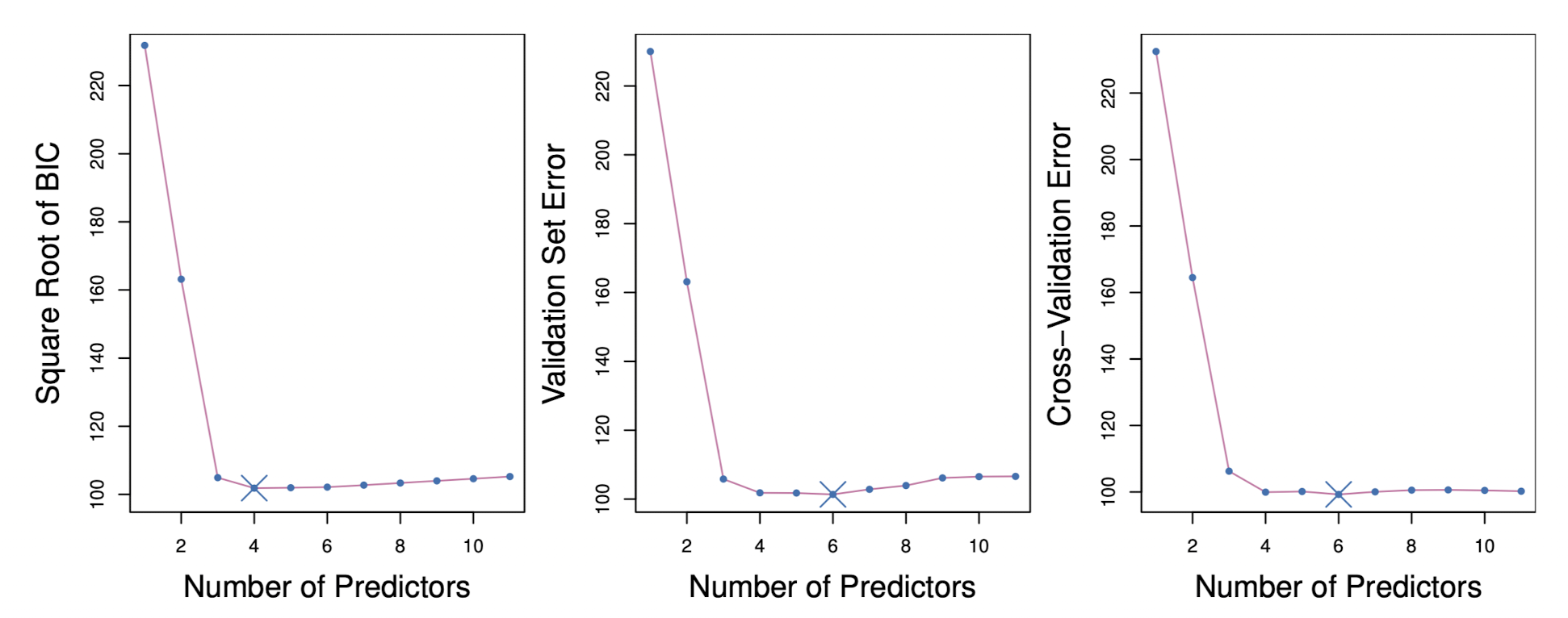
위 그림을 보면 BIC, Validation Set, CV를 이용한 방법에서 각각 4개, 6개, 6개의 설명변수를 사용하는 모델을 선택했다. 하지만 세 그래프 모두 4개, 5개, 6개의 변수를 사용하는 모델들의 Test Error가 비슷하다는 것을 알 수 있다.

그럼 Validation Set을 이용한 변수선택을 해보자. 우선 데이터셋을 Train과 Test로 분리한 뒤, Training Data로 모델을 적합한다.

> set.seed(1)
> Hitters = na.omit(Hitters)
> dim(Hitters)
[1] 263  20
> train = sort(sample(1:263, 132))
> test = setdiff(1:263, train)
> regfit.best = regsubsets(Salary ~., data = Hitters[train,], nvmax = 19)
> test.mat = model.matrix(Salary ~., data = Hitters[test,])
> val.err = rep(0, 19);val.err
 [1] 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0

적합한 모델의 Test MSE를 계산한다.

> for (i in 1:19){
+   coefi = coef(regfit.best, i)
+   yhat = test.mat[,names(coefi)] %*% coefi
+   val.err[i] = mean((Hitters$Salary[test] - yhat)^2) # MSE
+ }
> val.err
 [1] 188190.9 163306.2 152365.0 164857.0 152100.7 147120.0 148833.0 155546.5 167429.2 169949.1 173607.9 173039.5 168450.4 169300.5 169139.3 173575.1 175216.2
[18] 175080.2 175057.5
> which.min(val.err)
[1] 6

1개부터 19개까지의 설명변수를 사용하는 모델에서 Test MSE를 계산한 결과 6개의 변수를 사용하는 모델이 최적인 것으로 나타났다.

이번에는 K-fold CV를 이용해보자.

> k = 10
> set.seed(1)
> folds = sample(1:k, nrow(Hitters), replace = T)
> table(folds)
folds
 1  2  3  4  5  6  7  8  9 10 
28 22 24 24 30 26 25 24 31 29 

이렇게 10개의 fold를 만들었다. 각 fold에서 1개부터 19개의 변수를 갖는 모델의 MSE를 계산해보자.

val.err = matrix(0, nrow = k, ncol = 19)
for (j in 1:k){
  best.fit = regsubsets(Salary ~., Hitters[folds !=j,], nvmax = 19)
  test.mat = model.matrix(Salary ~ ., data = Hitters[folds==j,])
  for (i in 1:19){
    coefi = coef(best.fit, i)
    yhat = test.mat[,names(coefi)] %*% coefi
    val.err[j, i] = mean(((Hitters$Salary[folds==j]) - yhat)^2)
  }
}
> val.err
           [,1]      [,2]      [,3]      [,4]      [,5]      [,6]      [,7]      [,8]      [,9]     [,10]     [,11]     [,12]     [,13]     [,14]     [,15]
 [1,]  98623.24 115600.61 120884.31 113831.63 120728.51 122922.93 155507.25 137753.36 149198.01 153332.89 155702.91 155842.88 158755.87 156037.17 157739.46
 [2,] 155320.11 100425.87 168838.35 159729.47 145895.71 123555.25 119983.35  96609.16  99057.32  80375.78  91290.74  92292.69 100498.84 101562.45 104621.38
 [3,] 124151.77  68833.50  69392.29  77221.37  83802.82  70125.41  68997.77  64143.70  65813.14  65120.27  68160.94  70263.77  69765.81  68987.54  69471.32
 [4,] 232191.41 279001.29 294568.10 288765.81 276972.83 260121.22 276413.09 259923.88 270151.18 263492.31 259154.53 269017.80 265468.90 269666.65 265518.87
 [5,] 115397.35  96807.44 108421.66 104933.55  99561.69  86103.05  89345.61  87693.15  91631.88  88763.37  89801.07  91070.44  92429.43  92821.15  95849.81
 [6,] 103839.30  75652.50  69962.31  58291.91  65893.45  64215.56  65800.88  61413.45  60200.70  59599.54  59831.90  60081.48  59662.51  60618.91  62540.03
 [7,]  85793.95  78506.34  80541.35  84213.50  87140.78  80669.98  86247.85  89643.01  92081.37  89057.16  88102.28  90885.98  95025.99  99172.32  99314.04
 [8,] 273084.54 235423.66 230706.43 205624.81 223867.35 205559.00 206556.77 182678.23 179783.18 179916.36 173790.82 180508.48 185424.38 183257.89 183331.01
 [9,] 178316.69 163857.60 142998.75 120697.54 115261.58 108791.71 102320.25  89418.23  84366.23  80188.72  80665.49  82509.05  85078.50  89243.38  90478.82
[10,] 131492.54  95111.58 104956.38  96978.66  91377.54  73322.28  71687.88  66524.07  63281.82  62320.54  66011.39  65086.73  66097.41  73444.48  72351.39
          [,16]     [,17]     [,18]     [,19]
 [1,] 155548.96 156688.01 156860.92 156976.98
 [2,] 100922.27 102198.69 105318.26 106064.89
 [3,]  69294.21  69199.91  68866.84  69195.74
 [4,] 267240.44 267771.74 267670.66 267717.80
 [5,]  96513.70  95209.20  94952.21  94951.70
 [6,]  62776.81  62717.77  62354.97  62268.97
 [7,] 100192.99 100302.79  99772.60 100659.75
 [8,] 185159.62 183643.63 182587.35 183436.78
 [9,]  91782.20  91723.08  91140.55  91344.82
[10,]  71311.99  71393.23  71333.19  71417.75
> test.mse = apply(val.err, 2, mean)
> which.min(test.mse)
[1] 10

19개의 모델 각각의 평균 Test MSE를 구한 결과, 10개의 설명변수를 사용하는 모델이 가장 최적의 모델인 것으로 나타났다.

> reg = regsubsets(Salary ~., Hitters, nvmax = 19)
> coef(reg, 10)
 (Intercept)        AtBat         Hits        Walks       CAtBat        CRuns         CRBI       CWalks    DivisionW      PutOuts      Assists 
 162.5354420   -2.1686501    6.9180175    5.7732246   -0.1300798    1.4082490    0.7743122   -0.8308264 -112.3800575    0.2973726    0.2831680

10개의 변수를 사용하는 회귀식에서는 AtBat, Hits, Walks, CAtBat, CRuns, CRBI, CWalks, DivisionW, PutOuts, Assists가 선택되었다.