AI/DL/ML (11) - L2 regularization

Contents

1. L2 regularization
2. Hyperparameter: alpha
3. Graphical analysis

---

1. L2 regularization

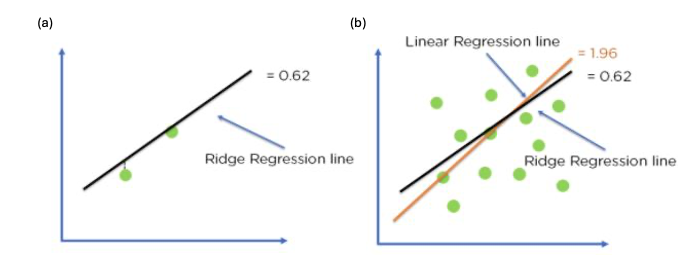
An L2-regularized linear adds coef$^2$ as the penalty term.

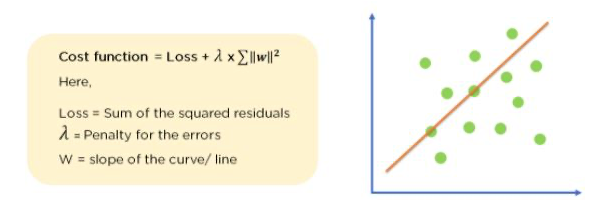
L2 regularization 은 가중치의 제곱을 벌칙으로 부과한다. 특히 이를 선형 회귀에 적용시킨 경우 "Ridge" 라는 명칭을 얻게 된다. 아래에 보이는 것과 같이 Ridge regression 을 통한다면 가중치가 너무 높아지지 않도록 하여 더욱 일반화된 모델을 얻을 수 있다.

Optimization of model fit using Ridge Regression

이전과 동일한 방법으로 sklearn 에서 제공하는 Ridge() class 를 통해 55개의 특성을 가지며 표준화 처리가 완료된 훈련 데이터를 다시 학습시켜보자.

print(ridge.score(train_scaled, train_target)) # 0.9899079889758701
print(ridge.score(test_scaled, test_target)) # 0.9801025763153384

---

2. Hyperparameter: alpha

Ridge() class 도 Lasso 와 동일하게 "alpha" 라는 parameter 를 갖는다. 그렇다면 저번처럼 alpha_list 를 만들어 적절한 규제 강도를 찾아가보자.

alpha_list = [0.001, 0.01, 0.1, 1, 10, 100]

for alpha in alpha_list:
  ridge = Ridge(alpha=alpha)
  ridge.fit(train_scaled, train_target)
  train_score.append(ridge.score(train_scaled, train_target))
  test_score.append(ridge.score(test_scaled, test_target))

---

3. Graphical analysis

상용로그로 alpha 를 변환해주면 다음과 같은 그래프를 얻는다. 이전의 Lasso 와 비교해 훈련세트와 테스트세트의 차이가 훨씬 적어진 것이 눈에 띈다. 특히 alpha = 10 에서 둘의 차이가 가장 작고 이후부터는 훈련세트에 대한 점수가 급속히 감소하므로 이 점에 대해 다시 regularization 을 해보자.

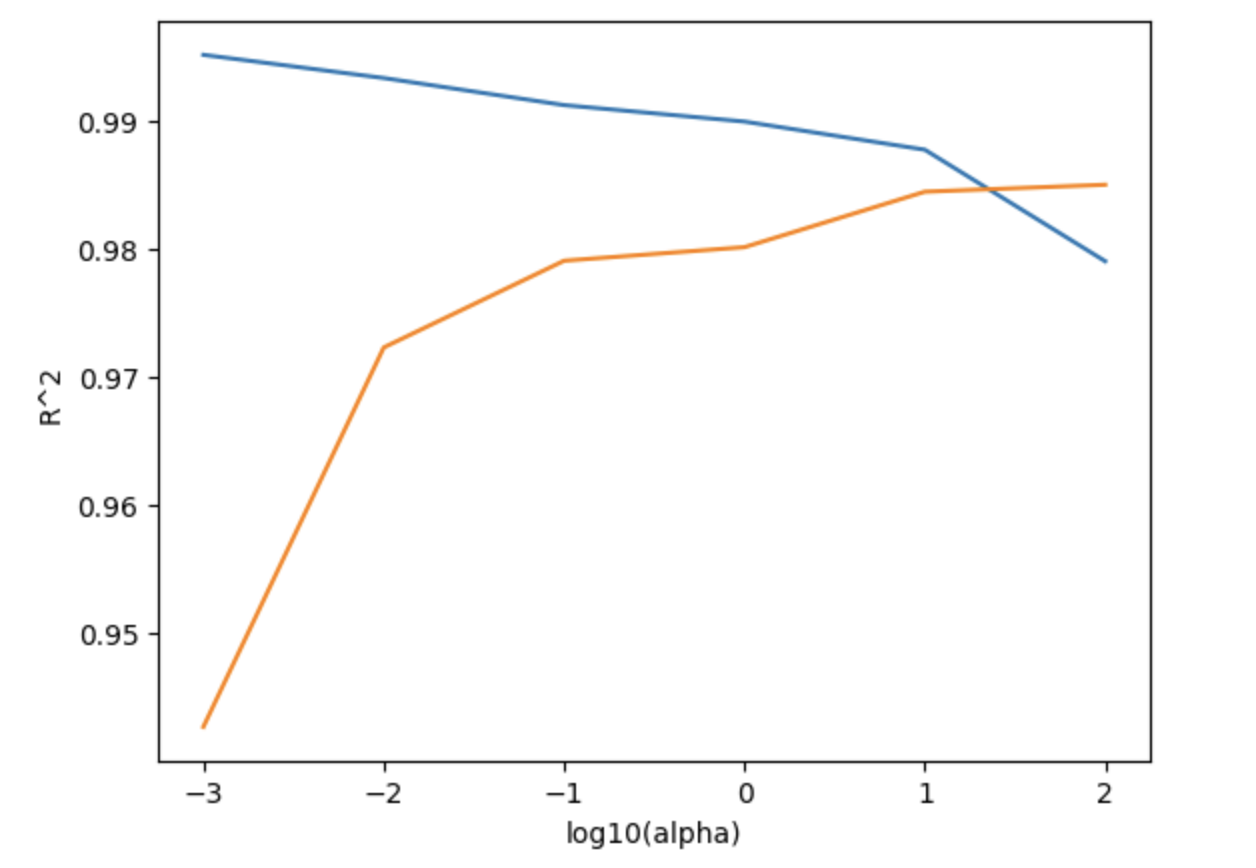
ridge = Ridge(alpha=10)
ridge.fit(train_scaled, train_target)
print(ridge.score(train_scaled, train_target)) # 0.9877112612906505
print(ridge.score(test_scaled, test_target)) # 0.9844320330213309

그렇다면 train score 가 살짝 낮아졌지만 해당 trade-off 를 통해 우리는 두 점수의 차가 L1 보다 더욱 작아졌음을 알 수 있다.

---